パソコンユーザーのためのDRAM入門目次

Part 1 : パソコンにおけるDRAM、DRAMの構造
Part 2 : 制御、パッケージ
Part 3 : GHzへの挑戦、PCB
Part 4(準備中) : マルチチャンネル、規格、未来

Part 2 おさらい

Part 2の肥大化を抑えるために、Part 2ではDRAMチップの制御方法の大枠と、DRAMダイのパッケージングについてのみ触れた。そろそろ肉眼スケールの話に移りたいと飽き飽きする頃だろう。

そして、ついにPart 3で私達人間が日常的に触れられる物理スケールの話に移っていく。いよいよDIMMのご登場だ。ついにcmオーダーの話に突入だ。だが、ここには悪魔が潜んでいる…いや、もはや神と言っていいだろう。そう、電磁気のお時間が始まります。どんなにデジタルな数字を扱おうとも、その根源には物理法則があることを叩きつけてくる、それが現実の厳しいところである。噛み締めろ、現実の苦さを。

信号伝達速度の限界 : GHzへの挑戦

2021年に生きる私達は「CPUのクロック周波数が4GHzで～」「メモリクロック周波数が1.2GHzで～」「そのWi-Fi 2.4GHz？5GHzの方がいいよ？」とGHz単位で動く製品を日常的に利用している。この当たり前に使っている「GHz」という単位、一見ただの高い周波数程度に見えるが、この世界にはkHzやMHzとは全く異なった世界が広がっているのだ。この世界を知るとあなたはこうつぶやくだろう。

「光はあまりに遅すぎる。遅刻しないでほしい。ってか真空の誘電率、高すぎね…？」

あなたが想像する「電気信号」のイメージを書き換えることにはなるかもしれない。

「光速」それはこの世界を律する神の定数

まずは物理のお話をする必要がある。と言っても、私の能力的にそんなに深い話はできないし、深い話をここで書ける能力があるのなら、私はその能力を用いて本を出版しているだろう。なので、身構える必要はない。

アインシュタインの特殊相対性理論により正の質量をもつ物質が光速以上にはなれないことが示されており、そしてそれはかなりの精度で高い事実であることはよく知られているであろう。この真空中の光速cは物理学の中でもトップクラスに重要な物理定数だ。そして光速を超えられないのは情報伝達においても同じである。現時点で光速を超えて情報を伝達できる媒体はない。

なお時々、量子エンタングルメントを用いれば情報伝達が光速を超えて行えるという話があるようだが、私が知る範囲では、観測した結果が遠隔地で特定のパターンに瞬時に収まるという話であり、観測結果そのものを制御、伝達できるわけではない。詳しい人の補足があればコメントを期待する。

半導体エレクトロニクス分野での信号伝達は電気や電流を媒介とする方式と電磁波(電波、赤外線、可視光線)を媒介とする方式に大きく分けられる。2021年を生きる皆様にとってどちらも大変なじみ深い技術のはずだ。このQiitaの記事を読むために使った技術の中にはほぼ確実に両方が入っているだろう。そして、DRAMとその周辺の通信は見ての通り前者に分類される。Siフォトニクス技術を駆使したオンボード光通信はそれはそれで(物理的にも)熱い領域なのだが、まだ2021年に生きている我々のパソコンでは採用されていない。ごく普通に導体をつないで通信をしている。

電磁波がほぼ真空中の光速(約30万km/s)で伝わることは周知の事実であろう。いわゆる1秒間に地球を7周半回ることができる速さである。では、電気信号が伝わる速さはどれぐらいであろうか？実はこれもほぼ光速である。多くの大学の理工系学部1年生の教養物理でマクスウェル方程式をもとに計算させられるやつである。波動方程式と聞くと「うっ、頭が」となる理工系学部出身の方も多いだろう。私もそうである。電磁波も電気信号も電磁気力であり、電場、磁場の相互作用で伝わっていくことになる。

そこで勘のいいひとは気が付いたはずだ。「あの計算には誘電率と透磁率が出てきたような…？」大正解である。現実の部品では真空中とは誘電率が透磁率が違う上に複数の部品が複合しているため、その解は真空中とは異なる。じゃあマクスウェル方程式を解きましょう…ということはせずに、すでに計算済みの解を用いる。ただ、あなたが電子回路に慣れていないならある常識を捨ててもらう必要がある。

低周波の常識が通用しない高周波の世界

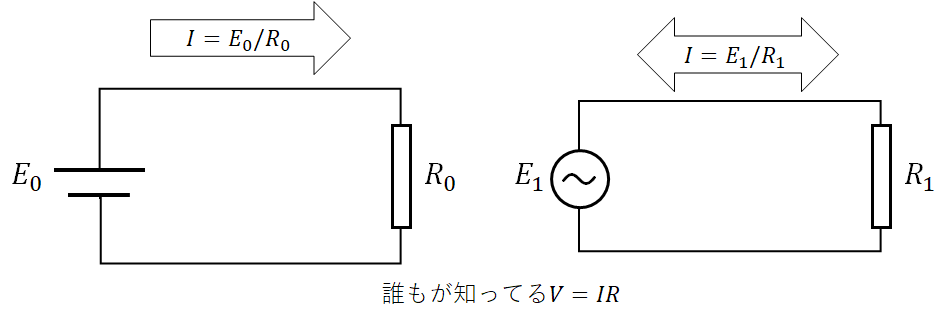
オームの法則、日本の義務教育にも組み込まれている電気に関する基礎中の基礎となる法則だ。知らない人はいないであろう。

電源(電池など)と負荷(抵抗など)をループしてつなぐことで、電圧=電流×抵抗、すなわちV=IRが成り立つという法則だ。これは高校物理に入って交流電流をやった場合でも概ね成り立つ。キャパシタンス(コンデンサ)やインダクタンス(コイル)による位相遅れなどはあれど、ある意味オームの法則の延長で話を進めることができる。抵抗による分圧もオームの法則で説明が付く。それこそ、電気工事士の試験範囲もこれで収まっている。一つの施設の中を商用電源程度の周波数を通すだけであれば、普通の人が持っているであろう電気の常識が通用する。負荷の抵抗を上げれば電流は減るし、並列つなぎすればより多くの電流が経路に流れる。コンデンサなどでの位相前後はあれど、割と常識的なふるまいをする。電源と負荷の組み合わせが流れる電流や電圧を決定する。

だが、これらがすべて近似だといわれたらどう思うだろうか？

直流の回路や商用電源の配線で私たちはある大事なものを無視している。それは「大きさ」である。電源も抵抗もコンデンサもコイルも回路図の上では大きさが表現されていない。そして、その回路図を現実に落とし込んだ時に最も大きいはずのものの大きさをも無視している。そう、配線、すなわち「伝送路」である。私たちが回路図に線を引いたとき、その線の長さに意味はないし、分岐していない線の両端で電圧も電流も位相も同じとみなしている。ただ、これが成立するのは波長に対して十分に回路が小さい場合のみである。もし波長に対して回路が十分な物理的な大きさを持っている場合、私たちはただの導線に対してもその大きさを考慮に入れないとその振る舞いを予測できない。

そして、GHzオーダーで動く今のDRAMは明らかにその近似が成立しない領域で動いるのだ。この領域では導線の長さ、太さ、形状が電気の振る舞いを大きく変える。GHz、それはデジタルがアナログと混じり合った極限の世界なのだ。

低周波であるがあまりにも大きすぎる電力系統

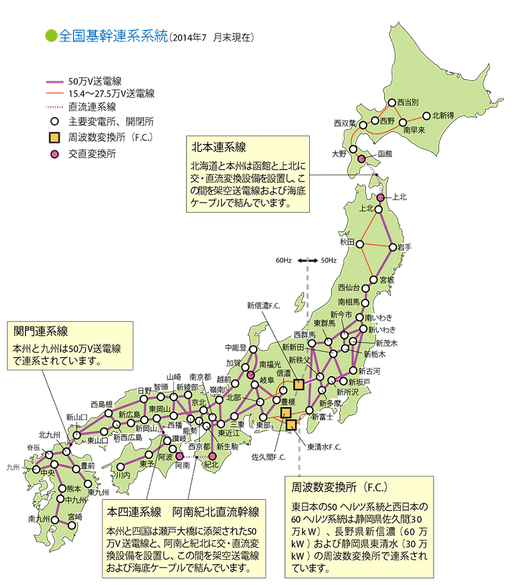
いきなり高周波に入る前に、なじみ深い低周波回路で話を進めよう。身近で最も物理的に大きな回路と言えば？そう、電力系統である。皆が生活するために常に必要とされ、文字通りの社会基盤であり、大きさ量ともに圧倒的な交流回路の代表例である。

https://www.fepc.or.jp/enterprise/supply/soudensen/index.html より引用

数多くの大規模発電所と多数の変電所、そして数多の建物と機器とを連結している電力系統はおおよそ1000kmほどの規模を持った巨大な回路だ。そこに流れる電気の周波数は西日本では60Hz、東日本では50Hzである。とりあえず近似で電気の速度を光速とすると、波長はそれぞれ5000km、6000kmだ。規模が波長を上回りはしないものの、無視することはできないし、実際場所によって位相は異なる。もし1000kmを端から端まで一方向に送電したら、両端で70度近くの差が生じることとなる。もちろん発電所も負荷も遍在しているため、電力が流れる方向も一定ではなく結果として両端でそこまで差は出ないが、災害などで大規模な発電、負荷変動が起きると…？

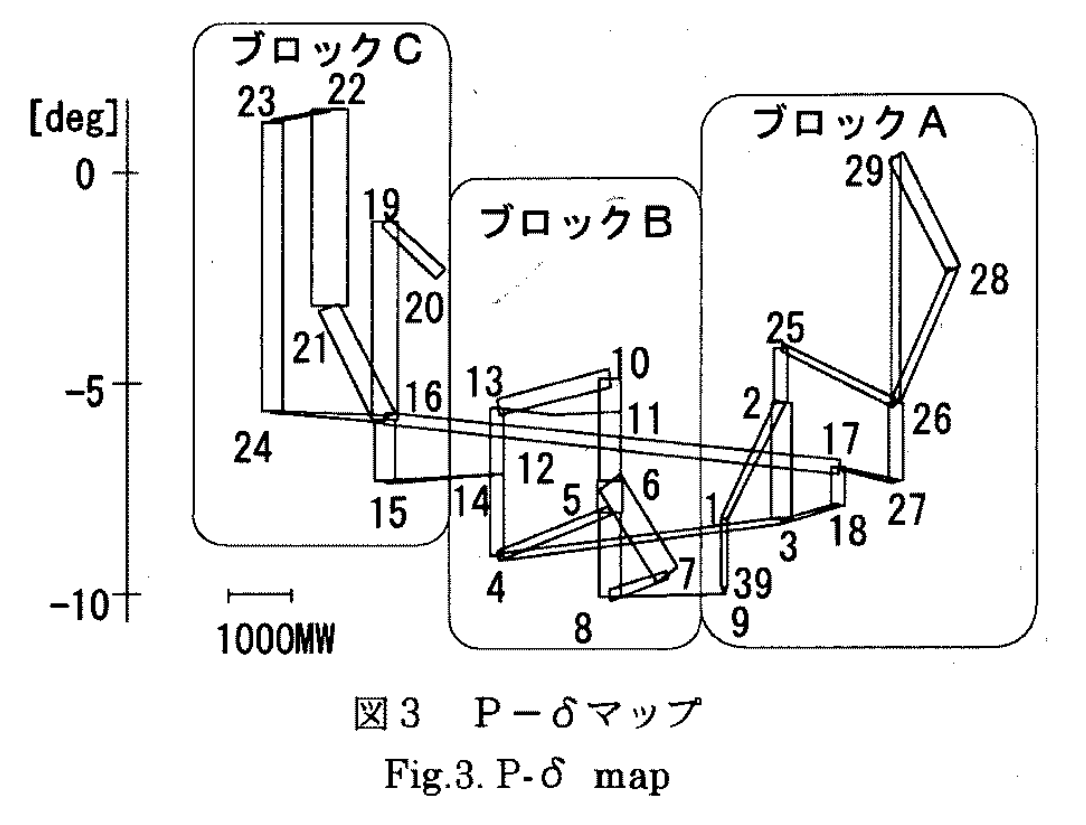
これに関して「電力系統の潮流計算結果と安定度計算結果の視覚化」という東京電力の人が書いた面白い論文があったので紹介しよう。

電気の流れ、すなわち潮流を可視化するという話なのだが、そこで提案されている可視化例が大変わかりやすい。

複雑に入り組んだメッシュ状の送電網において、位相が進んでいるところから位相が遅れているところに電気が流れるという傾向がある。いや、この書き方だと因果関係を想起させてしまうが、V=RIと同じで、定常状態においてそのような関係が見られるということだ。この図において、概ね上から下に電気が流れていく。注意してほしいのはすべて電圧の位相であり電流の位相ではないであることだ。負荷のキャパシタンスで電流の位相が進むという話ではない。日本ではなくアメリカの例ではあるが、電気の流れの向きの変化は場所による位相が変動することでもあることをこの論文ではよく可視化している。送電網には巨大な波がうねっているのだ。

回路が巨大であること、単にその大きさがその振る舞いを変え、分析を困難にしてしまうのだ。

集中定数回路と分布定数回路

直流や低周波回路のように、回路の大きさを無視できる回路のことを「集中定数回路」と呼ぶ。これは、部品のところに例えば抵抗やキャパシタンスなどの定数が集中している、と捉えることができるという意味でこの名前が付いている。一方で、回路の大きさを無視できない回路のことを「分布定数回路」と呼ぶ。端的に言えばこれは抵抗やキャパシタンスなどの定数が回路中に広く分布しているものとして捉えることだ。一般に「高周波回路」というと分布定数回路というのだが、低周波と高周波の間になにか明確な境界があるわけではない。先の回路規模に依存するというのもそうであるし、それなりに大きい回路だったとしても、位相などの細かい分析がいらないというケースもあるだろう。ただ、目安として小型の回路でもその設計に高い難易度を要求してくるようになる目安として"GHz"という周波数が出てくるわけだ。

さて、回路の物理的な大きさが回路設計の難しさを変えるという話をしたが、それはどういうことなのか簡単に説明しよう。きちんと知りたい人は「高周波回路設計」などで調べて本を買ってみるのが一番だが、ここはパソコンユーザーが気軽にライトにほへーと知識欲を満足できる程度で説明していく。

馴染み深い直流回路や低周波回路において、その振る舞いを決定するのは電源と負荷だ。これは前述の通りだし、義務教育でもやるし、普通の認識だろう。だが、高周波回路でその振る舞いを決定づけるのは、電源と伝送路だ。負荷は影響しない…というよりは負荷が振る舞いに影響をしないように設計するというのが多くの場合の設計のゴールとなる。これはどういうことなのか？高周波回路設計の触りがわかる簡単な例題を提示する。

上のような10Vの直流電圧源と10Ωの抵抗を2本の3mの導線でつないだごくシンプルな回路がある。この回路で電源をつないでから1ns,20ns,40ns経ったとき、右端の抵抗は何W消費しているだろうか？もちろん、ある程度時間が経った後であれば「流れる電流は1Aなので10Wだ」と答えられるだろう。だが、1nsというのは光でさえも30cmしか進めない時間だ。そう、電源が生じた電圧はまだ右端の抵抗には届いていない。よって1ns後は0Wだ。ここまでは簡単に答えられる。だが、20nsは…？

20nsも経てばさすがに電圧は右側の抵抗に伝わっている。ならその瞬間に1A流れ始めるのだろうか…？もしそうだとすると、その1Aという電流はどこから生まれたのだろうか…？抵抗に電圧が伝わるより前の時点では、電圧源は負荷がどうなってるかを原理的に知ることはできない。最低でも電圧源が1Aを放出できる道理はない。その状況でもし本当に1A流れるとするなら、突然導線から1Aの電流が生じたことになる。そんな馬鹿な…？そもそも、1ns後に電源は何Aの電流を吐き出したんだ…？明らかになにかが足りない。そう、両端をつないでいる3m、ここの電気的特性をもっと理解しないとさっぱり挙動がわからないのだ。

先程述べたように、高周波回路のようにとても短いタイムスパンでの電気の挙動を理解するためには、回路を駆動する電源とその周辺の伝送路の特徴をきちんと捉える必要がある。遠くにある負荷の情報は電源には伝わってこない以上、必然的に伝送路がその振る舞いを決定する。ここで大変重要になってくるのが「特性インピーダンス」だ。アマチュア無線をやっている人なら馴染み深いはずだ。「D型50Ω同軸ケーブル」などと言ったときの「50Ω」だ。なお、単に「インピーダンス」と言ったときのものとは意味が違うのでそこは要注意である。なので、特性インピーダンスのことをインピーダンスを略するのは本当にご法度である。まあよく見るけど…。

高周波回路設計の話ならゴリゴリ計算をするのだろうが、ここはあくまでお気持ちで楽しむ場なので、量の話は忘れてどんどんミクロの視点に降りていこう。

電気が伝わるとは

あなたは電気が伝わるということに関してどういうイメージを持っているだろうか？もしかするとかなり人によって違うかもしれないし、そもそも電気は電気だろという感じの人も多いだろう。もちろん、回路設計においても電気は電位や電流と言った抽象的な数字として取り扱うことになるのだが、なぜ電気がその様に振る舞うのかという根本的な物理を抑えないと、単に上から降ってきた知識で計算作業するだけになってしまう。それは理解とは言わないだろう。

電気とは電磁気力によって引き起こされる様々な現象の総称である。雷や静電気といった自然現象から電灯やモーターを動かす人為的なものなど幅広い現象がある。これの根源である電磁気力は19世紀に急激に解明が進み、James Clerk Maxwellによるマクスウェルの方程式によりその挙動がほぼ完全に説明できる様になった。科学的探求の末に電磁気力は一般に「電気」と呼ばれる現象だけでなく、もっと幅広い物理現象の根源であることがわかった。光も電磁気力によるものであるし、そもそも物質がその形状を保っていられるのも電磁気力のおかげだ。熱が伝わる、ガスが燃える、代謝する、ほぼあらゆる現象が電磁気力によるものだ。例外は重力と核エネルギーぐらいであろう。日常で起きることほぼ全てを電磁気力が司っていると言っても過言ではない。電磁気力が支配的であるのは、私達が「物質」と呼ぶものが電荷を持った粒子によって構成されているからだ。皆さんご存知「陽子」と「電子」だ。

この2種類の粒子は電荷を持つ粒子であるために「荷電粒子」と呼ばれ、その電荷の量は「電気素量」という物理定数となっており通常eと表記する。(ちなみに、電気素量が物理定数になったのは2019年である。)陽子の電荷は+eで電子の電荷は-eだ。身の回りの物質は通常は陽子と電子の数がほぼ同じ数だけ含んでおり電荷を打ち消し合っている。

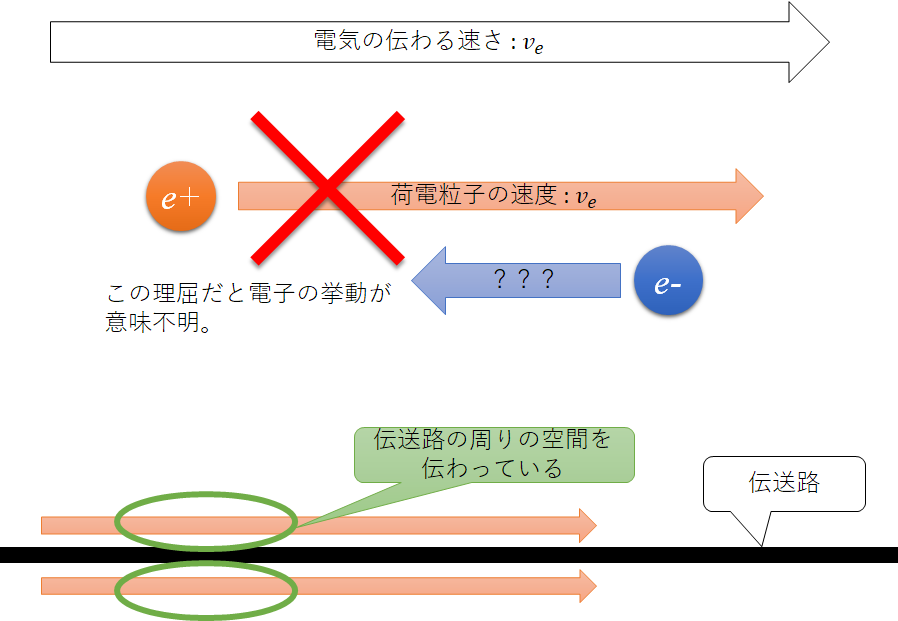
私達が「電流」と呼ぶ量はこの荷電粒子の移動の量を示している。なら「電気が伝わる」というのは荷電粒子がその速度で移動するということなのか？いやいや、少し待ってほしい。電子は小さいながらも質量を持っている。天下り式だが、精密なオシロスコープで観測すると、細かくは条件によるが電気は光速の50%以上の速度で伝わる。電子をこの速度に加速するには100keV(キロ電子ボルト)ほどのエネルギーを電子に与える必要があり¹、必要な電圧はその定義通り100kV、つまり10万ボルトだ。しかも、電子の加速を妨げるものが存在しない前提である。だが現実にはそんな電圧をかけなくたって電気は猛スピードで伝わるし、そもそも速度は電圧に依存していない。さらに、この理屈だとプラス電極の周辺の金属では「電子の減圧」が起きることで、電子を吸い込んで電気が伝わるということになる。いくら自由電子とはいえそれだと全然遠くに伝わらない。電気は荷電粒子の移動によって伝わっているのではない。

では、どのように伝わっているのか？電気は導体ではなくその周辺の空間を伝わっているのだ。「何を言ってるんだお前は？」と言われそうだが、順を追って説明しよう。なお、この説明は不正確になってるがご容赦願いたい。というのも、題材にしたような代数関数で表せられない電位変化を解析するのは私の力量では難しく曖昧さが残る。(というか、数値解析が必要となる。ご興味がある方は OpenFDTD などでの数値シミュレーションを試してみると大変おもしろいのではないかと思う。)

まず、(古典的な)電磁気力の本質的な振る舞いは空間そのものの場にあることをきちんと抑える必要がある。いわゆる電場と磁場である²。真空中を電磁波が伝わるようにこの2種類の(ベクトル)場は媒質を必要としない。今でこそ当たり前に高校物理でも出てくる知識だが、これは日常的な物理現象と比較するとかなり特異な性質であり、電磁波の伝達に媒質がないことを示したマイケルソンはこれに関する功績でノーベル賞を受賞したほどインパクトのある発見である。電気が伝わるとはこの電場と磁場の変動が伝わっていくということに相当する。受信端の部品の周辺の電磁場の変動により部品の荷電粒子が動き「電気が来た」と感じることとなる。

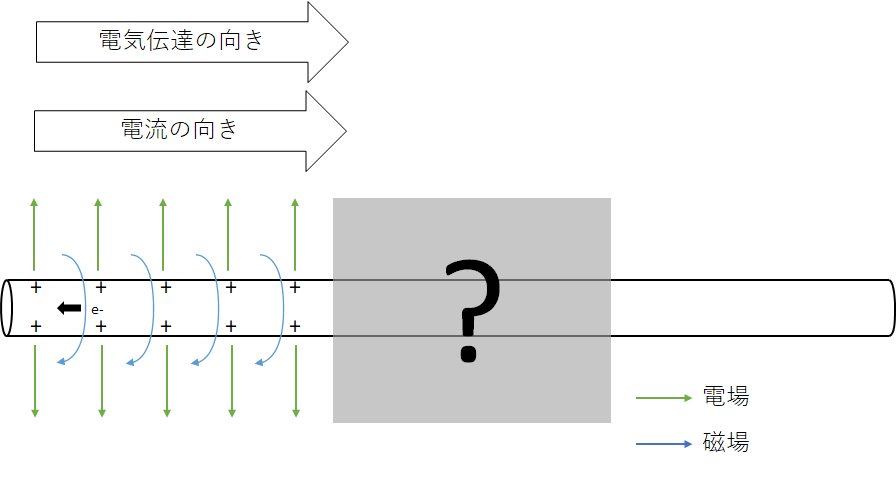
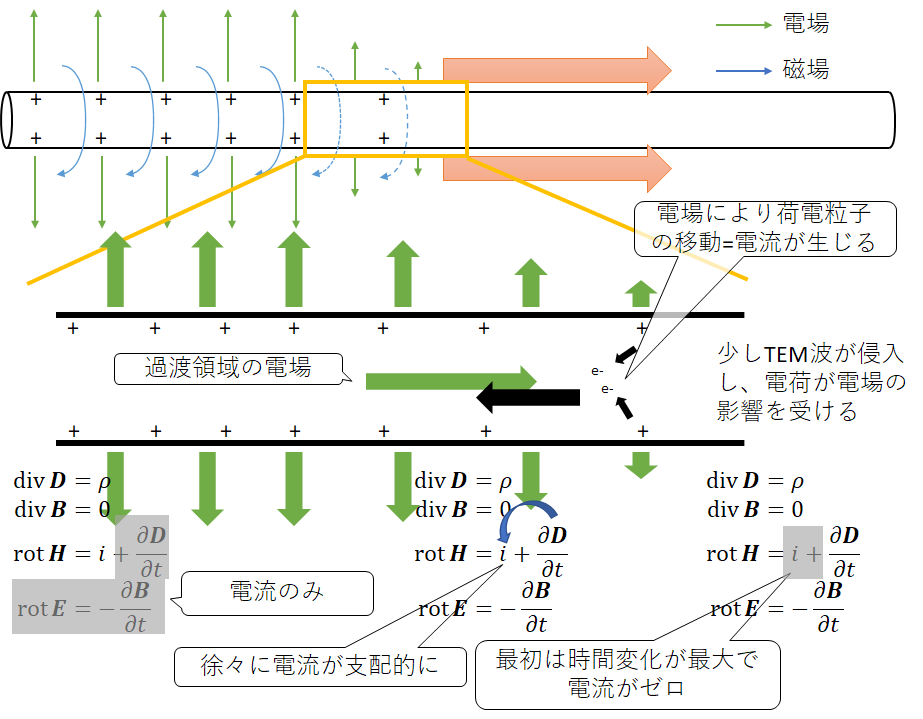
細かく説明するためにまず状況を設定する。真空中にまっすぐに左右に導線が伸びており、左側から一定の電圧をかけて、それが右に伝わっていくとする。電流の向きは電気伝達の向きと同じとする。つまり、電子は逆向きに動く。精密な議論をするわけではないので、とりあえず雑に同心円状のむき出しの銅の線を想像してもらおう。ただ、ミクロ目線かつ動磁場における電位というのは荷電粒子が生じる電場と電磁誘導により生じる電場が混ざりややこしいので、とりあえずは「電場の矢印の根っこ」ぐらいの認識にしてもらおう³。初期状態として図の様に左側にのみ電場、磁場が形成されているものとしよう。この部分の表面からは少し電子が減り、表面と内部の電位が上昇している。逆に右側は特に変動がないものとする。今回注目したいのはその間の過渡状態の部分だ。

ここを真面目に計算をすることは究極的に困難なことが容易に想像つくと思う。金属導体に絡むマクスウェル方程式の解法は大抵の場合は金属表面は等電位であることを前提としている。だが、過渡状態ではこの前提は成立しないため、解析を困難とする。ただ、(結果論的だが)今回は周辺の真空のほうが主役だ。

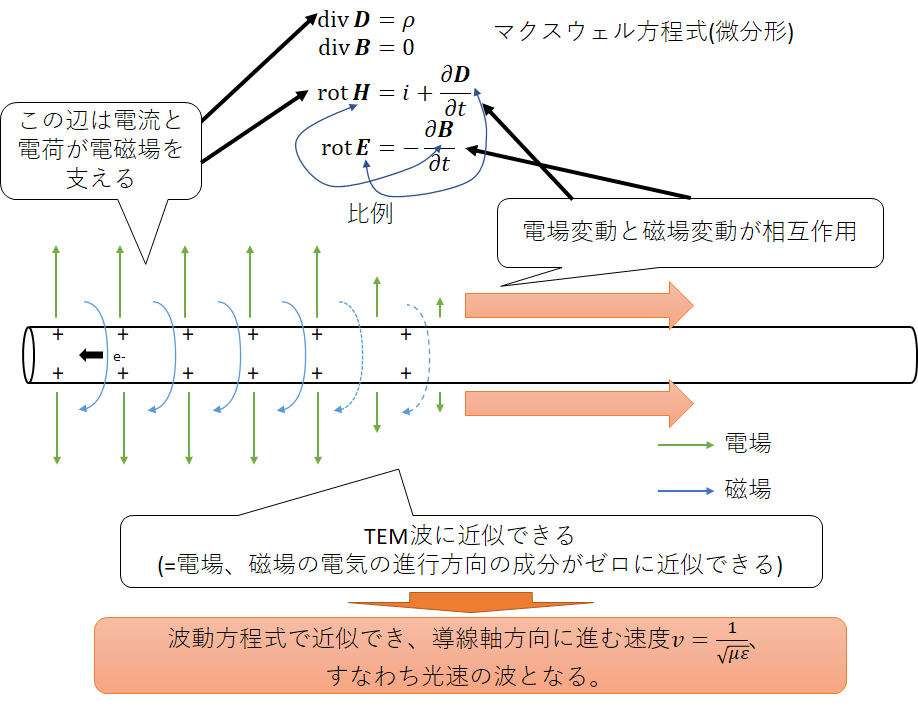
この真空の領域、すなわち導線の表面ではない近傍では各点での振る舞いは典型的な電磁波の進行と起きることは同じである。この領域において、電場は導線から同心円状に放出する向きに時間が立つにつれ増大する。この電場増大は電流と同様の振る舞いをし磁場の回転と対応する。同時に磁場の増大も起きており、これが電場の回転と対応する。図中に示したマクスウェル方程式の第3,4式が主にその振る舞いを示すこととなる。この第3,4式の電場と磁場の相互作用はどちらかがどちらかへの因果関係を示していそうだが、これはあくまで各点においてそのような関係が満足されるという意味でしかないことを念の為付しておく。

そして、その電場、磁場の導線軸方向の成分はほぼゼロに近似できる。これは単に前提として左側から平面状に電磁場が来たということに依拠しており、いささかトートロジー的な感じがするが、数段落の間はこれを受け入れてほしい。そして、これらを統合するとこれは教科書的な平面電磁波の振る舞いであり、その伝達速度も皆さんご存知光速となる。(計算は各種電磁気学の教科書におまかせする。)この様に横波によってのみ構成される電磁波をTEM(Transverse Electric and Magnetic)波と呼び、特定の条件を満たす電気信号は伝送路をTEM波として進行し、様々な伝送の中でこれが最も速い。これはつまり、あまりに周波数が高かったり、伝送路がでかすぎるとTEMではない伝わり方をするという意味なのだが、さすがにDRAMではそんな狂った振る舞いはしないので安心してほしい。

うまいことCGが作れないのだが、導線を電気が伝わるということは、磁場の渦がまるで導線を飲み込むようにシュシュシュっと光速で吸い取っていき、同時に電場変動(≒電位変動)も伝わっていくという物理現象なのだ。

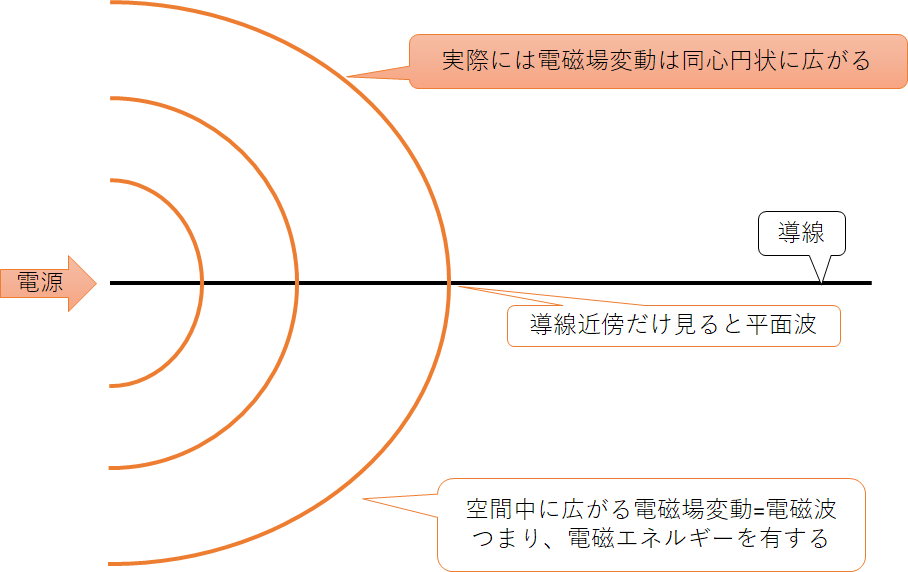
ただ、いくつかの疑問点があるだろう。まずは先程お預けした「平面の仮定」だ。度々「近似」という単語を連呼している通り、これは厳密ではない。現実の導線には端っこがある上に孤立していないので、平面波というのはかなり都合が良い強い仮定だ。

導線である以上電気を印加する場所はごく小さな部分であり、そこで生じた電磁場の変動はすべてが導線沿いに進むわけではなく、同心円状に広がっていくことになる。導線の近傍に存在しない電磁場変動は当然導線の反対側につないだ部品を動かすことはなく、空間中に放出されることになる。

「えっ、そんなバンバン電磁波放出したらものすごいエネルギー損失になるんじゃ…」

と思ったあなたは勘が良い。すなわちこれは「アンテナ」なのだ。エネルギーを導線から外に電磁波という形で放出するものがアンテナであり、最もシンプルなアンテナであるダイポールアンテナはただの金属棒である。電気伝達という目的から見ると、電磁波を放出することは効率の悪化に見えるが、逆にアンテナとして見るとそれは効率が良いアンテナということになる。なお、無策に電気を通すだけだとどっちつかずな無用な物体が出来上がってしまうのが現実の悲しいところで、設計者は伝送路は伝送路として、アンテナはアンテナとして工夫しないと使い物にならないのである。

ここまでのことからいろいろなことがわかる。まず電気の伝達速度を決定するのは導線の材質ではなく周辺の空間、すなわち現実的には周辺の誘電体(絶縁体)であることがわかるだろう。これは現実に確認されている電気伝達速度の傾向と一致している。電気信号の伝達速度は周辺の誘電体の誘電率に依存しており$v=1/\sqrt{\mu _{0} \varepsilon}$(なお、$\mu _{0}$は真空の透磁率、$\varepsilon$は誘電体の誘電率)である。

この数字はビニールなどで被覆された導線とむき出しの導線では信号伝達速度が数割ほども違うことも示している。空気の比誘電率はほぼ1であり、むき出しの導線ではほぼ光速で電気が伝わるが、例えば一般的なPVC被覆だと物によっては比誘電率が4近くになる。これは信号伝達速度が約半分に低下することを示しており、高周波信号を取り扱う場合においてこの両者の違いは致命的に重要になってくる。1GHzで30cmもあると、まるっと1波長分遅延が異なることになる。これは凄まじい違いだ。実際に高周波回路設計において基板の材質は大変重要なパラメータとなる。

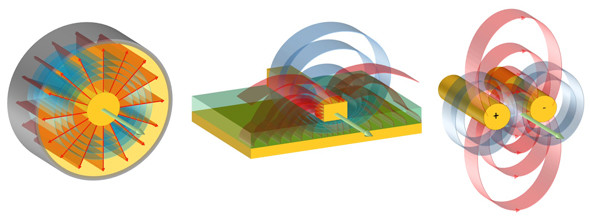
そして高周波において、なぜ同軸ケーブルの特性が例えばツイストペアケーブル(LANケーブルや電話線で利用される)など他の伝送路と比べて良いのかが直感的に理解できる。導線に沿って進行する電磁波を生み出せるのは、導線に対して垂直な電場とそれに伴う磁場だけである。それ以外の向きの電磁場は導線以外の方向にエネルギーを伝えてしまう。下の図の様に同軸ケーブルはきれいな同心円状の電場を形成するため、外向きや進行方向軸の磁場を形成せず、きれいなTEM波として伝わる。一方、マイクロストリップラインなどは外側に広がった丸まった電場を形成するため、進行方向軸の磁場も形成してしまう。結果、電磁波が外部に放射されてしまうのだ。実際にはこの電磁エネルギーによる放射損失が伝送損失全体において支配的になることはまずない。ただ、放射ノイズ源として問題になることは確かにあり、これは大変頭が痛い設計上の課題となる。

上図は https://ednjapan.com/edn/articles/1910/08/news013_2.html より引用。左から同軸ケーブル、マイクロストリップライン、差動ペア平行線ケーブル

ここまで来ると、それこそマザーボードなどのプリント基板に見える配線がこれまでとは別物に見えてくるはずだ。本当に注目するべきは配線そのものではなく、配線の周囲の空間だったのだ。高周波回路における配線とは電磁波を纏いながらそれを導く役目を担っている。少し前に通信を電気や電流を媒介とする方式と電磁波を媒介とする方式に分類したが、ミクロな目を持つとそれらは共通したメカニズムで動いていて、その実態はすべて電磁波での通信と言える。

ところで、導体内部での電位伝達はどうなっているのだろうか？導体内部では電気伝導率が真空と比べて非常に大きいため、電場は拡散によって伝達する。ここでは省略するが、一定の条件でマクスウェル方程式を解いた電信方程式において、電気伝達率が小さいと波動方程式に近似でき、電気伝達率が大きいと拡散方程式に近似できるという特徴がある。ただ、拡散による伝達はTEM派による伝送と比較すると遥かに遅い。そのため、導体周辺のTEM波に誘導される形で電場の拡散と電荷移動が起きることになる。

かなり無理があるのだが、簡便に図示してみた。TEM波は進行方向軸に進むがある程度は導体内部に侵入する。全く侵入しないとすると、第1式の発散が微分不可能となり、電荷密度無限大などというとんでもないポイントが爆誕してしまう。侵入したTEM波は荷電粒子、この場合は電子の移動を引き起こす。このときに、電気の有無の境界である過渡領域には左から右への電場が生じていることに注意すると、電子は左側に加速され、結果として右方向の電流が生じ始めることとなる。なお、よく静電場における導体の解析では「導体中に電場は生じない」としているが、今回は静電場ではないのでその前提は成り立たない。この電気の流れはじめのフェーズでは、マクスウェル方程式第3式の電流の項はゼロであり、純粋に電磁相互作用の振る舞いを示す。すなわち、磁場を支えているのは純粋に電場の変動だけだ。その後、先程加速された電子により電流が生じ始めると、徐々に電流の項が支配的になる。一方で、電場変動や磁場変動は徐々に減衰する。そして、最終的に電場と磁場の時間変動はなくなり、磁場を支えるのは電流のみとなる。ちなみに、rot Eは図示が難しかったが、電場の増加量に相当する振る舞いを見せる。定常状態になればここも当然ゼロだ。

無理に説明したので、いささかごまかしが入っているが、電気が伝わる様子というのがより鮮明になったのではないだろうか？

特性インピーダンス

さて、現実の伝送路は孤立した導体ではない。大抵は電流が返ってくるための導体が繋がっている。というよりは、返ってくる導体がない場合は前述のようにアンテナとして振る舞ってしまう事となる。使い物になる伝送路は行きと帰りがある。これは平衡でもシングルエンドでの伝送でも共通の事項だ。この場合、ここまでの説明で出てきたどこか空間に消えて言ってた電場のベクトルの行き先は返ってくる導体になる。つまり、2つの導体の間の電磁場が先程のTEM波を伝送することになる。この返ってくる導体というのは、具体的にはプリント基板の場合には「GND」になる。ちなみに、同軸ケーブルでは外部導体、ペア線の場合は対の相手だ。高周波回路において、このGNDをどう配置するかが伝送の特性における大事なパラメータとなる。

また、TEM波を想定すると進行方向軸の電磁場成分はゼロなので、断面によってその特性が決定することになる。つまり、断面を見たときの導線や誘電体の形状材質配置が伝送路の特性を決定する。このモヤッとした「特性」を具体的に示す数字はいくつかあるのだが、そのうち、最もよく注目されるのが「特性インピーダンス」だ。

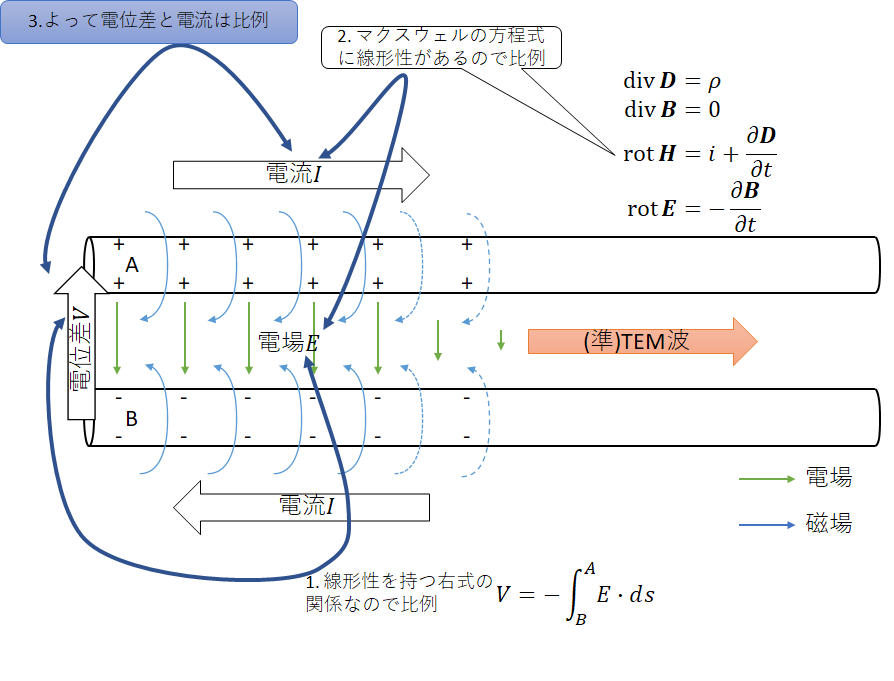
先程の導線の周囲の電磁場の図を返り線を追加して図示した。左側に電源が繋がった簡単なペア線である。このとき、死ぬほど大雑把に捉えると、上の線から下の線に向かった電場が形成される。さて、導線の形状が固定の場合、この電場の大きさは何で決まるだろうか？そう、ペア線の間の電位差である。距離が固定なら電位差と電場の強さは比例する。そして、マクスウェル方程式は線形なので⁴磁場なども比例する。導体中の電流は2本の導線間のTEM波によって誘導されたものであり、TEM波の物理量が2倍になれば流れる電流も2倍になる。つまり、2本の導線間の電位差とそこに流れる電流は比例するという関係があるのだ。この関係、オームの法則にそっくりだろう。交流回路における電位、電流の比率であるインピーダンスをもじって特性インピーダンスと名付け、単位も「Ω」だ。記号としては$Z_{0}$がよく用いられ、先の電位差と電流には以下の関係が成り立つ。

Z_{0} = \frac{V}{I}

これは理想的には長さに依存せず、断面によって決定する。なお、伝送路は単純に導線としての抵抗値やインダクタンスなどの普通のインピーダンスも持っており、こちらは当然長さに依存する。名前は似ていて、次元が一致するし、後述のマッチング対象ではあるのだが、別物なので要注意である。

ちなみに、厳密には特性インピーダンスは周波数に伴い変動するが、一定以上の周波数なら固定値で取り扱って問題ない。特性インピーダンスが問題になるような回路で、周波数による特性インピーダンスの変動が目に見えて起こることはまずないと言って良い。

さて、これは具体的にどれぐらいの値なのだろうか？現実に使われている伝送路の特性インピーダンスは概ね30-100Ωの範囲に収まる。なお、特性インピーダンスはその大小よりも揃っていることのほうが重要なパラメータであるために、先行で使われていた値だったり、通常の合理的な設計で作ったときの特性インピーダンスに統一したりといった方法で定まっている。数字感を掴むためにもいくつか例示しよう。(なお、ストリップラインはシングルエンドのみ想定)

同軸ケーブル
- 75Ω : JIS C 3501 に規格あり。テレビ受信用の機器等に主に利用。空気絶縁タイプの同軸ケーブルが源流らしい
- 50Ω : JIS C 3501 に規格あり。アマチュア無線や放送局など比較的大電力を通す分野で利用。ポリエチレン絶縁で作ると概ねこの値になる。
マイクロストリップライン、ストリップライン(PCBにおける配線)
- 36-60Ωぐらいがよく見る。幅などを変えることで、特性インピーダンスを制御できる。
ツイストペアケーブル
- 100Ω : LANケーブルなどで利用。電話線もADSL下りの周波数帯域ではこの特性インピーダンス。ADSL…あと数年で消えます。

むっちゃ余談なのだが、昔のPCI Expressは差動通信で差動インピーダンス100Ωを規格で要求しており、PCB設計者から「高すぎだろ！」と文句が出てたとかなんとか[要出典]

インピーダンスマッチング

さて、かなり遠回りしたが、序盤で触れた例題に戻ろう。ただし、今度はちゃんと伝送路の特性インピーダンスと伝送速度を指定する。

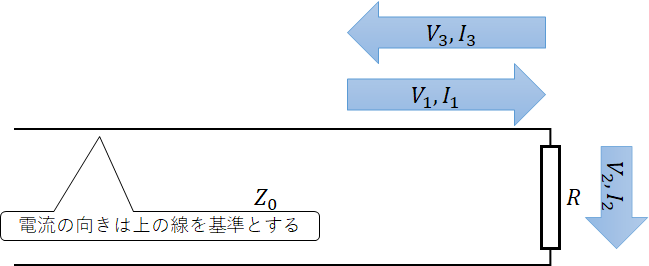
上のような10Vの直流電圧源と10Ωの抵抗を特性インピーダンス$Z_{0}=50Ω$、3mの伝送路でつないだごくシンプルな回路がある。(端がショートしているように見えるが、許して…。ちゃんとした回路です。)この回路で電源をつないでから1ns,20ns,40ns経ったとき、右端の抵抗は何W消費しているだろうか？なお、信号伝達速度は秒速20万km(光速の約2/3)とする。

ようやくここに戻ってこられた…。さて、まずは1ns後だ！

前述の通り、1ns後の消費電力自体は0Wだ。まだ抵抗まで電力は到達していない。ただ、次のステップを考えるために、この時点での状況を正確に整理しておこう。まず、信号伝達速度の条件から左端から20cmのところまで電力が届いていることが分かる。そして、特性インピーダンスの条件から、そこまでの区間に流れている電流が10V/50Ω=0.2Aであることもわかる。

さて、この電力は15ns後に右端の抵抗に到達することになる。そこで何が起きるか？もし電流全量が抵抗を通ったとしても、そこでの電圧は$10Ω\times0.2\mathrm{A}=2\mathrm{V}$である。残りの8Vはいずこに…？今回の条件の場合、結果として電力の一部が反射してくることになる。電力が抵抗に到達すると、電源から抵抗に向かって進む電力と抵抗で消費される電力、そして反射して電源に戻ってくる電力という3つの電力に分かれることになる。(反射によって後者2つに分かれると取れなくもないが、電源からの電力は継続して出力されている前提なので、3つとも継続して存在することになる。)

さて、この3つの電力はどのような関係にあるだろうか？まず、電力と行ったがこれは電圧と電流で構成されているために、ここには6つの変数があることになる。以下のように設定しよう。

V_{1},I_{1}:電源から進行する電力(入射電圧、入射電流) \\
V_{2},I_{2}:抵抗で消費される電力(透過電圧、透過電流) \\
V_{3},I_{3}:抵抗で反射される電力(反射電圧、反射電流)

電源電圧、伝送路の特性インピーダンス$Z_{0}$と抵抗のインピーダンス(≒抵抗値、$R$とする)からすぐに以下の関係がわかる。反射電力も伝送路を流れる以上、その電力と電流の比率は特性インピーダンスによって決まり、そして抵抗ではご存知おなじみオームの法則が成り立つ。

\begin{align}
V_{1}&=10\mathrm{V} \\
I_{1}&=\frac{V_{1}}{Z_{0}}=0.2\mathrm{A} \\
V_{3}&=Z_{0}I_{3} \\
V_{2}&=RI_{2}
\end{align}

次に伝送路との抵抗の境界において成立する条件を考えよう。これに関しては一般にキルヒホッフの法則として知られている。まず電圧に関しては境界の両側で等しいという条件が成立する。過渡状態はともかく、電力が通過したあとは電源がないところで電圧は連続する。一方で電流に関してはその保存則が成り立ち、流入する電流と流出する電流は同量である。数式にすると以下の通りである。

\begin{align}
V_{1} + V_{3} &= V_{2} \\
I_{1} - I_{3} &= I_{2}
\end{align}

これを反射電圧、電流に関して整理すると以下の通りになる。

\begin{align}
V_{3}&=\frac{R - Z_{0}}{R+Z_{0}}V_{1} \\
I_{3}&=\frac{R - Z_{0}}{R+Z_{0}}I_{1}
\end{align}

このときの係数$\frac{R - Z_{0}}{R+Z_{0}}$を反射係数と呼び、$\Gamma$(ガンマ)とよく書かれるので、この記事でもそれを使う。今回の例題の条件では負荷端の反射係数は$\Gamma=2/3$である。ここから計算すると15ns後に電力が抵抗に到達して、そこで反射したあと20nsの時点では、伝送路右向きの電力が当初の通り10V、0.2A、逆向きの反射が約-6.7V、約-0.13A(左向きにマイナスなので右向きに正の電流であることに注意)、そして問題となっている抵抗では約3.3V、約0.33Aで約1.1W消費している。定常状態の10Wと比べるとその約1割しかまだ送れていない、という不思議な結果になっている。

そしてこの後、負荷端で反射した電力は今度は電源側に到達して、電源端でも再度反射することになる。今回は問題を簡単にするために、電源側にインピーダンスを設定しなかったので、短絡相当の振る舞いを示す事になり⁵、反射係数は-1となる。ただ、この電源端への到達は30ns後であり、それがまた負荷端に届くのは45nsであるため、例題となっていた40ns後の時点では20nsと同様の約1.1Wだ。

…え？知識欲が満たされない？このあとどうなるか知りたいって？仕方ない。

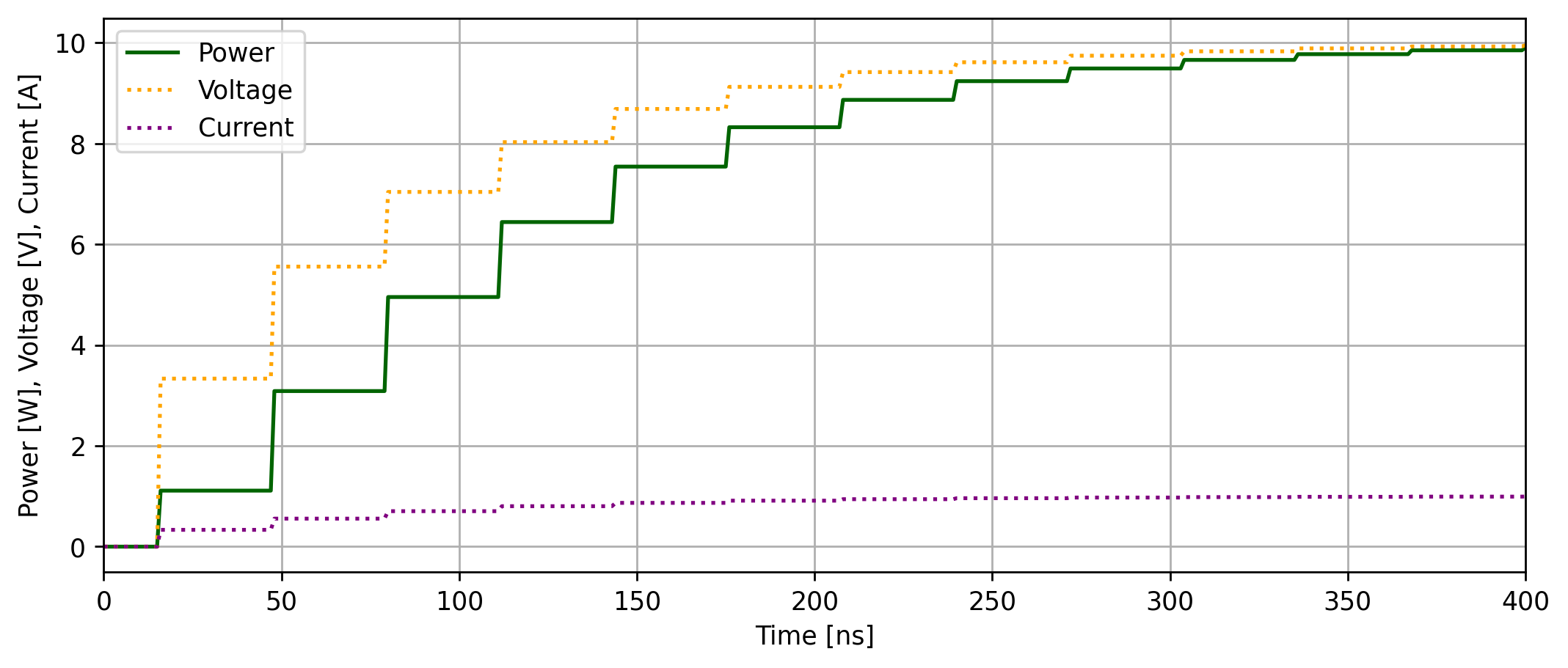
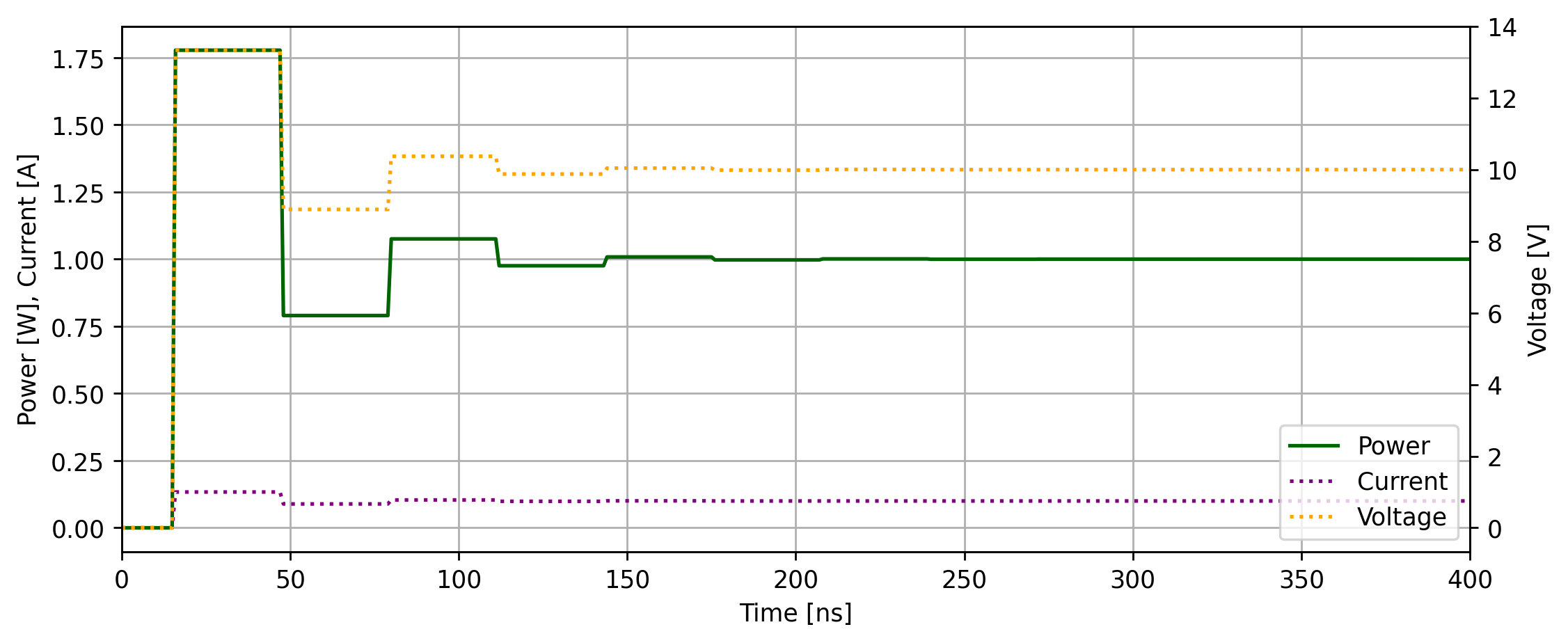
というわけで、お手製シミュレーションでグラフを出した。バグってたらごめん(グラフの形的に多分あってると思うが)。このグラフは負荷となっている抵抗で消費される電力、その電圧と電流の時間変化をプロットしたものである。電力が電源端と負荷端を往復しながら、最終的な消費電力である10Wに収束していく様子が目にとれるだろう。ちなみに、伝送路の特性インピーダンスよりも負荷の抵抗が高いときの様子も示しておこう。他の条件は同じで、負荷の抵抗だけ100Ωにしたときのグラフが下図である。値の大きさの問題から電圧だけ右の軸を使った。

一旦、最終的な状態よりも高い電力を消費したのち、振動を経て収束していく様子が見て取れる。

「ほう…面白い。でDRAMとどう関係するの？」という声が聞こえてきそうだ。ここで注目してほしいのは、かなり長いタイムスパンで電圧が上下に変動してしまっているということだ。これの原因は先の電力の反射であり、これが起きていることにより、電圧をかけたあとの伝送路の電圧がバタついてしまうのだ。かなり長いとは行ったがnsオーダーなので、直流や低周波であれば、ほぼ無視できる影響だが⁶、高周波回路でこれを無視することはできない。電圧がバタついているうちに次の信号が来るので、いろんな電気が混ざって全くワケワカメな状態になってしまう。

高周波回路の鉄則、それは電力を反射させないである。これは文字通り鉄の掟と言って良いとても大事な設計上の課題である。この電力の反射に関してDRAMのDIMMを見たら肉眼でわかる範囲で様々な工夫が凝らされている。つまり、DIMMを手にした状態でこの記事の頭からここまでをマッハで音読することで友達を吹っ飛ばせる。

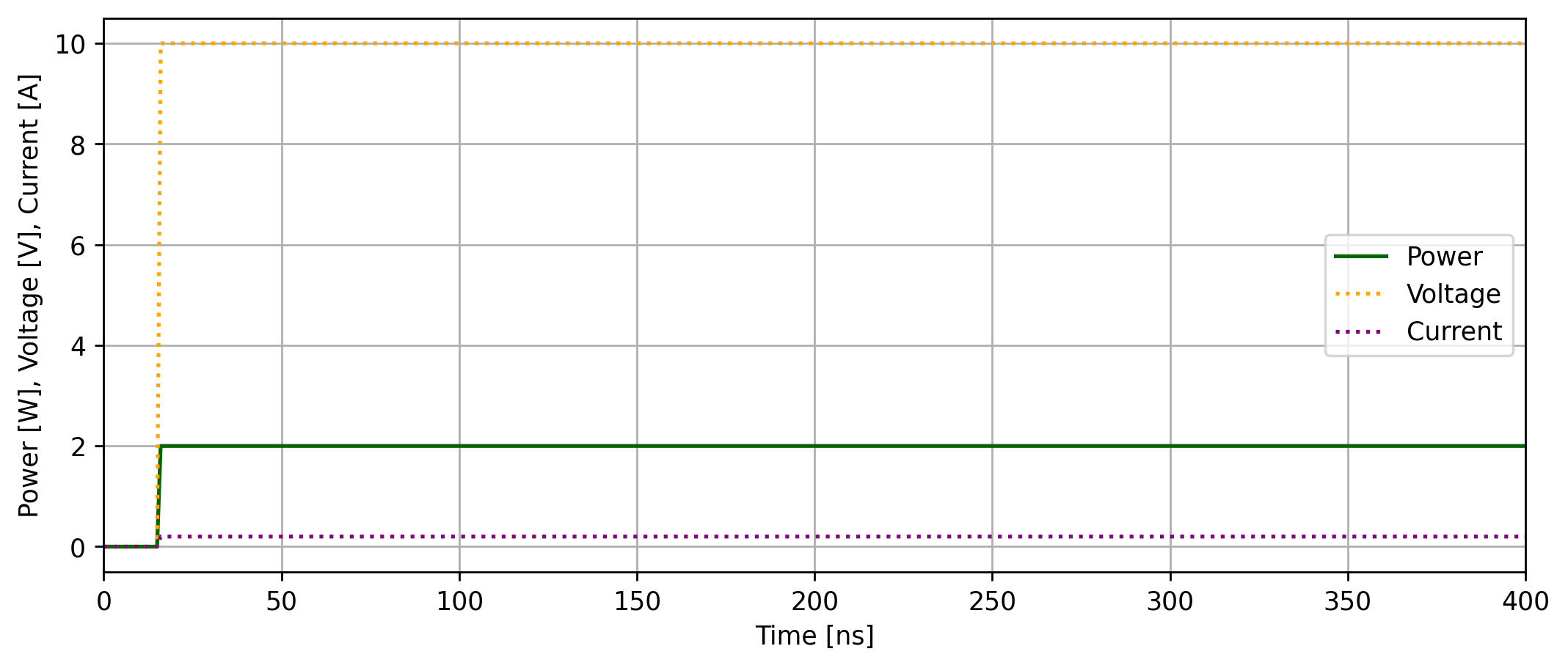
さて、電力を反射させないためにはどうするか？先の反射係数$\Gamma$を0にすれば良いことになり、見ての通りその条件は$Z_{0}=R$だ。このときには先のグラフは下図の様になる。信号が最初に到達する時間である15nsのあときっちり安定した電力を届けられている事がわかる。

このように、特性インピーダンス、インピーダンス(単純な抵抗の場合は抵抗値に一致)を揃えることで信号の反射を無くすことをインピーダンスマッチングと呼ぶ。そして、特性インピーダンス同士の場合にもこのインピーダンスマッチングは重要になってくる。先の反射係数の計算はよく見ると伝送路同士の接続でも全く同じであることがわかると思う。

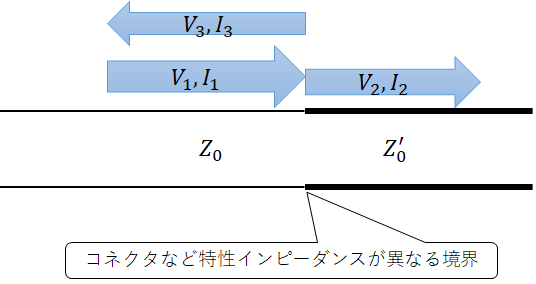
伝送路の途中の点の左側の特性インピーダンスを$Z_{0}$、右側の特性インピーダンスを$Z_{0}'$とすると、先の反射の計算を$R := Z_{0}'$と置き換えたときと同じことが起きるとわかる。違いは抵抗の場合は電力は消費して熱として消えていたが、伝送路の場合はそのまま右側に抜けていくことだ。すなわち、その先に更に違う特性インピーダンスの伝送路があったり、抵抗があったりすればまたそこでも反射することになる。そして返ってきた電力も、その途中で(特性)インピーダンスが揃っていない点を通過すると再反射することになる。

また、「点」といったが、この反射の関係は伝送路上のあらゆる場所で成り立つため、徐々にケーブルの形状が変わるなどで特性インピーダンスが連続的に変化するところではもっと複雑な振る舞いを見せる。伝送路を単にデジタル伝送に使うDRAMのような場面ではこのような反射は百害あって一利なし、とにかく抑え込む必要性がある。

有限の信号速度とインピーダンスマッチングを意識しながら、いざDRAMチップを飛び出てPCBの世界へ向かおう！

DRAMのPCB

デスクトップパソコンにおいてDRAMに関するPCBはDIMMとマザーボードの2つになるだろう。ここではDIMMに注目しよう。というわけで、お手持ちのDIMMをご準備してください。できれば、2-RankのDDR4 non-ECC Unbuffered DIMMが良い。都合よくそんなもの落ちてないって…？というわけで、手持ちの写真をご提示しよう。

…ヒートシンク邪魔ですね。最近のデスクトップ向けDIMMはかなりの比率でヒートシンクが付いており、基板の大部分を見ることができない。スロットに差し込む端子の周辺と隙間からちょっと見える程度である。このDRAMは普通にパソコンに取り付けるので、バラすわけには行かないのでネットの資料から引用させてもらおう。

https://www.crucial.jp/memory/ddr4/ct16g4dfd8266 より引用

とは言ったものの、実際のところPCBの配線の多くを肉眼で確認することは難しい。高速デジタル通信に用いられるようなPCBは多層PCBとなっており、そして特性インピーダンスを制御するために大抵の配線は内側の見えない層を使っている。というわけで、設計図を見てみよう。

「えっ？そんなの手に入るの？これからPCB溶かすんじゃないの？」

と思ったかもしれない。実はDIMMに関してはこれそのものの設計図は手に入らなくても、JEDECがリファレンスとなるPCBの設計図を一部公開している。ただ、その前にまずはDIMMそのものの位置づけを再確認しておこう。

DIMMとDRAMチップの関係

DIMMには見ての通り複数枚のDRAMチップが搭載されている。今回はUnbufferedのDIMMなので、PCBの役目は専らそのチップたちとDIMM下部の端子を電気的につなぐことだけだ。ただ、どことどこをつなぐのかということが重要になってくる。Part 2で出てきたDRAMの信号線は大きく「制御系」「データ系」の2つに大別できる。(この用語はここでの独自分類なので一般的ではない)

制御系 : クロック、アドレス(バンク選択含む)、チップ選択(これだけ特殊)、アラートなど
データ系 : DQS、DQ(Part 2で説明済み)、DM、DBI関係

(若干見慣れない信号もあるが、そういうもんがあるんだなという認識でスルーしてほしい。)

この2種類、制御系の信号線はDIMMの端子から分岐してすべてのチップに分配してつながっているのに対して、データ系の信号線はPoint-to-Pointでつながっているという大きな違いがある。ここまで題材にしてきたDRAMチップはx8、すなわちDQが8本出ているタイプのもので、これを8枚組み合わせて使うことになる。この8枚全部に同じコマンド、アドレスをつなげると、同じクロックで8枚から8bitずつ、合計64bitが出てくる。書き込みの時は逆にメモリコントローラ側から64bit送出し8bitずつ1つのDRAMチップに伝える。百聞は一見に如かず、PCBの詳細を見ていこう。

DIMMのガーバー(Gerber)データ

DRAMの規格を策定しているJEDECはDIMMの参照実装となるガーバー、すなわちPCBの設計図を公開している。PCBのパターン設計図はよくガーバー(Gerber)データと呼ばれ、そのフォーマットは多くの場合同じくガーバーフォーマットである。Gerberというのは本来そのフォーマットを開発した会社の名前であり、メーカー独自のフォーマットではあるが、PCB設計図として事実上の業界標準となっている。例えば激安なことで有名なFusion PCBもGerberで受け付けている。そのため、フォーマットとともに設計図データという意味合いでも「ガーバー」と言ったりもする。ホッチキスとかテプラみたいなもんである。下記JEDECのページでも"sometimes referred to as Gerber Files"と書かれている。

ただ、Gerberはあまりに単純なフォーマットで、単体で多層PCBは扱えないし、それどころかデータとして「配線」という概念を持ち合わせていない。PCBの製造する装置に流すほぼ生の加工データなので、言ってしまえばpath要素だけで作られたSVGみたいなものである。というわけで、実際にはJEDECが配布しているDIMMの設計ファイルは今回の範囲においてはGerberではなく"Cadence Allegro PCB Designer"向けのファイルを使っている。ビュアーだけなら無料で配っているので、ぜひ各自でダウンロードしてみよう。下記記事もぜひ参考にされたい。

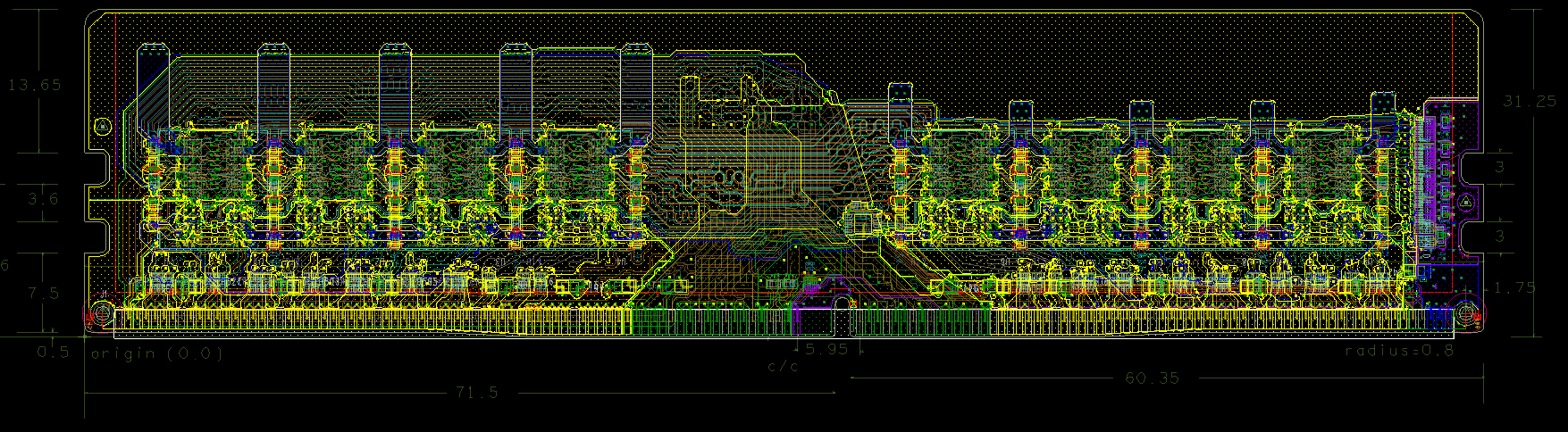
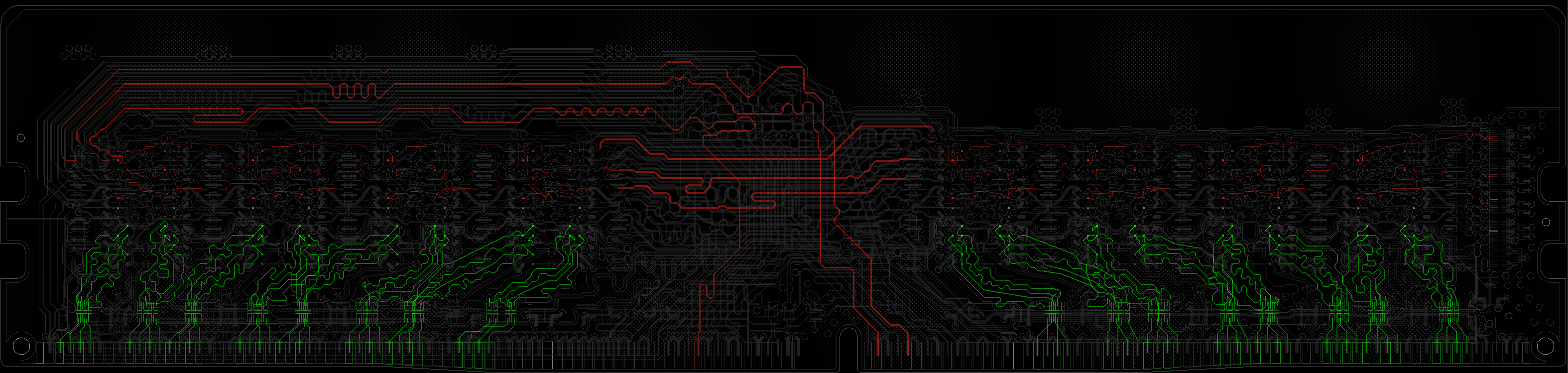
というわけで、ガーバーデータを開いたところが上の画像である。これまで説明してきたチップを搭載できるB2 Gerber(2 rank x8, planar, NON-ECC, UDIMM) を用いて説明していく。CADあるあるだが4Kディスプレイを駆使しても全然解像度が足りない…。多層PCBで線の数も多くかなり複雑である。さて、いくつか注目ポイントをピックアップしよう。

制御系とデータ系のトポロジの違い
等長配線(等遅延配線)のためのミアンダ配線
DRAMチップの向き
チップ抵抗によるノイズ対策
端子部の形状

なお、2 rankでDIMMの両面にDRAMが実装されているが、ランクの話はPart 4でやるのでとりあえずは16個のDRAMチップが搭載されているが、同時に動かすのは片面8個だけ、という認識で見てもらいたい。

制御系とデータ系のトポロジの違い

まずは先ほど分類した制御系とデータ系のトポロジの違いだ。PCBの配線のうち一部をピックアップして、制御系を赤色、データ系を緑色にして示す。

データ系はすごく端子から可能な限り短い距離でDRAMチップにつながっている⁷。特に分岐もないために単純だ。ここは双方向でDDRでデータをやり取りするために、信号周波数などの側面で制御系より設計がよりシビアにはなるが、接続も単純なためとにかく長さを短くすることが鍵になる。ただし、このDIMMのPCBの外側に分岐があるので、この緑の部分は伝送路からぴょこっとはみ出たスタブに相当する。このあたりは複数DIMMの話なのでPart 4に回す。

注目は制御系の方だ。こっちは信号を16枚のDRAMチップに分配する必要があるので、どこかに必ず分岐が必要になる。一箇所で一気に枝分かれして一直線に配線するのは空間の問題から無理なので、必然的に何段階に分けて分岐することになる。そのときにいくつか作戦が考えられる。

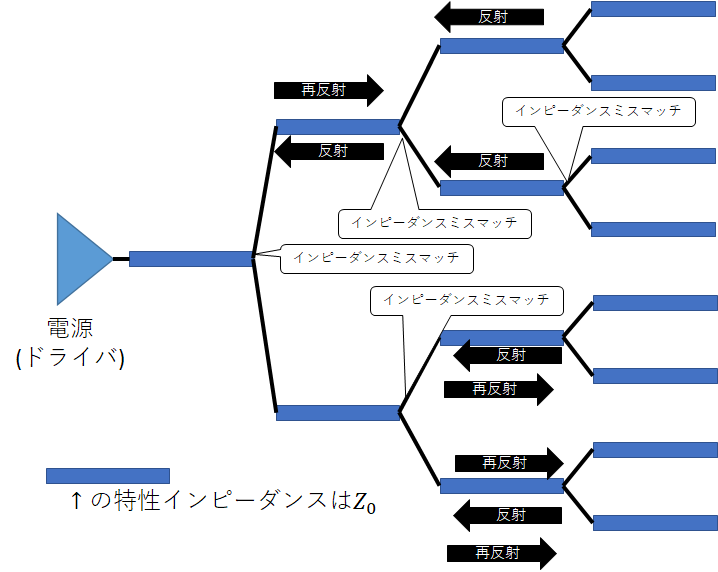
まず一つがDRAMチップをすべて同時に動かそうとする作戦である。このとき端子からの距離(≒遅延)を同じにする必要がある。この場合は下図に示すようなトーナメント式の配線が主な手法になる。この様にするとたしかに等遅延で信号が到達し、データ線も同時に動きとても簡単に動きそうに見える。

ただし、この手法は分岐におけるインピーダンスミスマッチの問題があるため信号の周波数が上がってくると問題を引き起こすことになる。特性インピーダンスの説明の時に、単に伝送路を一対一でつなげたときの反射の話をした。もし分岐があったらどうなるか？電源側伝送路、2つの負荷側伝送路の特性インピーダンスをそれぞれ$Z_{00},Z_{01},Z_{02}$、電源からの入力電圧、電流を$V_{0},I_{0}$、電源への反射を$V_{0}',I_{0}'$、負荷それぞれへの電圧、電流を$V_{1},I_{1},V_{2},I_{2}$として計算しよう。まずは電圧電流比

\begin{align}
V_{0}&=Z_{00}I_{0} \\
V_{0}'&=Z_{00}I_{0}' \\
V_{1}&=Z_{01}I_{1} \\
V_{2}&=Z_{02}I_{2}
\end{align}

次に境界条件

\begin{align}
V_{0} + V_{0}' &= V_{1} = V_{2} \\
I_{0} - I_{0}' &= I_{1} + I_{2}
\end{align}

このうち、特に$V_{1} = V_{2}$を利用して$I_{2}=\frac{Z_{01}}{Z_{02}}I_{1}$することで、以下のように書き直せる。

\begin{align}
V_{0}&=Z_{00}I_{0} \\
V_{0}'&=Z_{00}I_{0}' \\
V_{1}&=Z_{01}I_{1} \\
V_{0} + V_{0}' &= V_{1} \\
I_{0} - I_{0}' &= \left( 1+\frac{Z_{01}}{Z_{02}} \right) I_{1}
\end{align}

このうち、最後の式の右辺が負荷側に流れていく合計の電流量でありこれを$I_{1}'=\left( 1+\frac{Z_{01}}{Z_{02}} \right) I_{1}$と整理しなおすと、

\begin{align}
I_{1}'&=\left( 1+\frac{Z_{01}}{Z_{02}} \right) I_{1} \\
&=\frac{Z_{01} + Z_{02}}{Z_{02}}I_{1} \\
&=\frac{Z_{01} + Z_{02}}{Z_{01}Z_{02}}Z_{01}I_{1} \\
&=\frac{Z_{01} + Z_{02}}{Z_{01}Z_{02}}V_{1} \\
V_{1}&=\frac{Z_{01}Z_{02}}{Z_{01}+Z_{02}}I_{1}'
\end{align}

そう、並列つなぎした抵抗による合成抵抗と同じ式が特性インピーダンスでも成り立つのだ。そもそも合成抵抗の計算も同じ境界条件から出しているのだから当然といえば当然ではあるが。この合成された特性インピーダンスを$Z_{01}' = \frac{Z_{01}Z_{02}}{Z_{01}+Z_{02}}$として式を書き直すと、

\begin{align}
V_{0}&=Z_{00}I_{0} \\
V_{0}'&=Z_{00}I_{0}' \\
V_{1}&=Z_{01}'I_{1}' \\
V_{0} + V_{0}' &= V_{1} \\
I_{0} - I_{0}' &= I_{1}'
\end{align}

となるため、さっきと全く同じように、反射係数が設定できる。

\begin{align}
\Gamma& :=\frac{Z_{01}' - Z_{00}}{Z_{01}'+Z_{00}} \\
V_{0}'&=\Gamma V_{0} \\
I_{0}'&=\Gamma I_{0}
\end{align}

もし、分岐した2つの負荷側伝送路の特性インピーダンスが同じ場合は、特性インピーダンスが半分の伝送路を1つつなげたときと同じふるまいをすることになる。もしこの状況でインピーダンスマッチングをするなら、負荷側の伝送路は電源側に対して2倍の特性インピーダンスを持っている必要がある。基板パターンで調整可能なのは幅ぐらいなため、特性インピーダンスを2倍にするということは、ものすごく細くしないといけない。(対数が入ってくるため、一般に何倍、という数字は示せないが、特性インピーダンスはそうそう何倍も変えられるものではない。)これを4段もやるとなると、16倍もの特性インピーダンス差を持った伝送路を組み合わせるということになるために、これはあまりに絶望的な比率だ。トーナメント式での伝送路ではインピーダンスマッチングはあきらめる必要がある。これは信号品質を諦めることと同義であり、そうなるとGHzの世界で戦っていくことができない。どうしてもインピーダンスマッチングしながらトーナメントで配線したい場合、間にドライバとなる素子をはさんだりすることになるが、これはコスト増大につながるうえに、ばらつきを抑えることが困難であり、遅延をぴったりにすることが難しくなる。

そこで、DDR4は⁸Fly-by Topologyと呼ばれる接続形態をとっており、信号線自体は分岐なしですべてのチップの直下を通り、ごく短距離の引き込み線(stub)でDRAMチップと信号線をつないでいる。もちろんstubは短いとはいえ分岐であるので、信号の反射は起きるのだが、ここを極力短くすることで反射の影響を抑えることができる。なお、制御系の信号線はアラートを除きDRAMチップ側からの信号送信を考えなくて良い、という点も重要である。(アラートは高速にスイッチングしないので、信号品質に関してはそこまでシビアではない)

このあたりの信号品質に関しては、上記コラムが詳しい。ぜひご参考に。

だが、犠牲が伴う選択なのは言うまでもない。Fly-by TopologyによりDRAMチップにクロックが到達するタイミングがずれるため、DRAMチップの動作タイミングにずれが生じ、データ系の信号線の動作タイミングも線によって異なるという事態になる。このクロックタイミングのズレをclock skewと呼ぶ。このskewの特徴は同じ部品組み合わせなら、時間が経ってもほとんど変動しない点だ。つまり、起動時にメモリコントローラがclock skewを計測し、以降はその計測結果を用いてデータ系の信号タイミングを調整すれば問題なく駆動させることができる。

DRAMチップが最終製品に完全に統合されてskewを制御できている場合はコントローラ側に遅延を事前に設定するという荒業も可能なのだが、脱着可能なメモリコントローラ(CPU)、DIMMの場合はそうも行かないのでDDR4では特に書き込みの遅延を調整するWrite Levelingの機能が備わっている。読み取りも同様のLevelingが必要であり、こっちはDDR4にある決まった値を吐き出させる機能(MPR Page0)を使ってメモリコントローラが勝手にやる感じになる。一方で、書き込みに関してはDRAM側から状態をフィードバックしてもらいながらメモリコントローラ側で遅延を調整しないと行けないので、DRAM側の支援が要る。と言っても、メモリコントローラが吐いたData strobeの立ち上がりに合わせてクロックのHigh or Lowを返すという単純なものである。データシートに手順が書かれているので興味がある方はぜひご覧あれ。なお、遅延を制御すること自体は例えばInverter(Part 1で説明)などのセルを直列でつないで、その間にトランスミッションゲートを取り付け、適した遅延を実現するトランスミッションゲートだけenableにすればお好みの遅延を実現できる。やり方は色々ある。

この様に、Fly-byで繋がった制御系信号線を軸にデータ系信号線を駆動していく。GHzの世界では信号品質や信号速度に気を配りながら、基板と制御を統合して設計する必要がある。単に同じタイミングにしろ、というだけではものは作れないのだ。DIMMに流れる信号に対してより具体的なイメージが持てたのではないだろうか？

急がば回れ、遅延を揃えるミアンダ配線

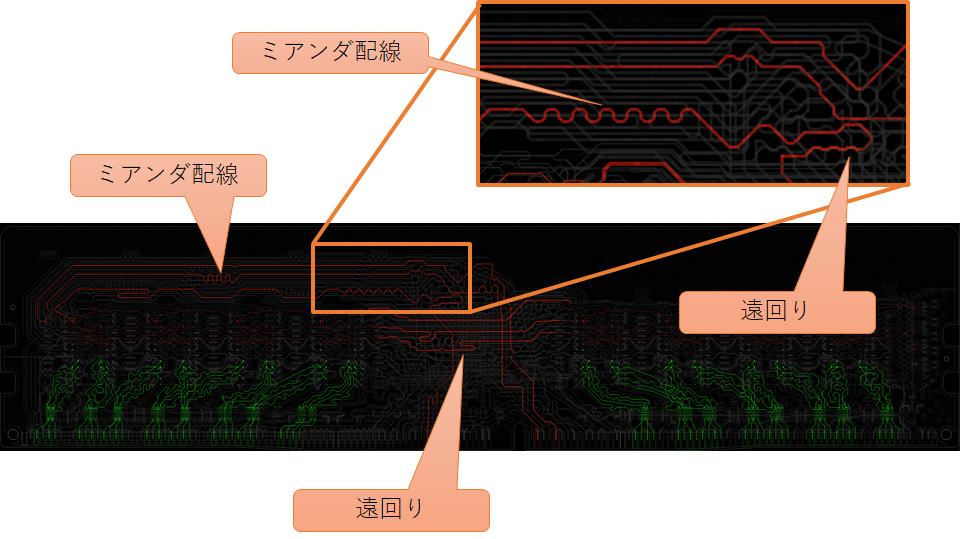
制御系信号の特徴は(アラートを除き)メインのクロック信号に同期していることだ。この時、DDR4では伝送路に許される遅延ばらつきは概ね数十ps(ピコ秒)のオーダーとなる。ちなみに、1000ps=1nsだ。信号伝達速度を用いて長さに換算すると1cmを切っており、これをDIMMスロットを搭載したマザーボードを含めて守る必要がある。マザーボード側に余裕を持たせてDIMMと他製品との相性問題を回避するには、DIMM側でその遅延ばらつきはほぼ全くと言っていいほど許容されない。マザーボードのCPU周辺は線が密集しておりほとんど取り回しの余裕がないため、DIMM側でskew marginを使い果たしてしまうともはや適合するマザーボードの設計は不可能となってしまうからだ。

そのため、上図のようにDRAMのパターンを見ると随所に遅延を調整するための遠回りが見られる。もちろん、データ系にも類似の制約はあるが、データ系は元から端子からチップまでの距離が短いので見た目にはわかりにくい。一方、制御系信号はDIMM内での長さが長いためにかなり引き回しを工夫しているところが分かりやすい。この中でも特にパターンを波打たせて遅延を稼ぐ配線をミアンダ配線と呼び、遅延を揃えるための定番パターンである。DIMM以外でもGPUやマザーボードでもお目にかかれると思うので、ぜひPCBをじっくり観察してみよう。

DRAMチップの向き : ピン配置とトポロジ

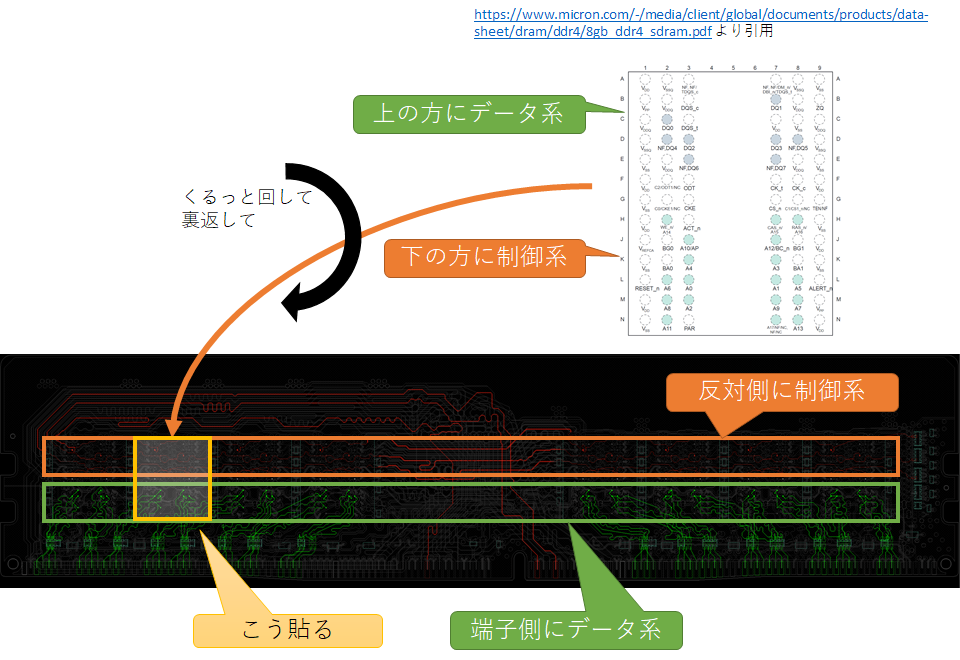
これは至極単純な話で、倍速で動くデータ系の信号線をなるべく下部に集中させるために、制御系は上に寄せてあるという話だ。

Part 2で載せたMicronのデータシートのFBGAピン割り当てを見直すと、図の上半分にデータ系、下半分に制御系が集中するように配置されている。これは、もちろんダイ側でレイアウトすると自ずとデータ系はデータ系で位置が偏る、という話でもあるのだが、DIMMのPCB設計を容易にするという意味で大変重要である。DIMMへの実装はこの図を上下反転させた向きで行われる。すると、端子側はデータ系、端子の反対側は制御系のピンが集まることになり、スマートなPCB配線がやりやすくなっている。

チップ抵抗によるノイズ対策

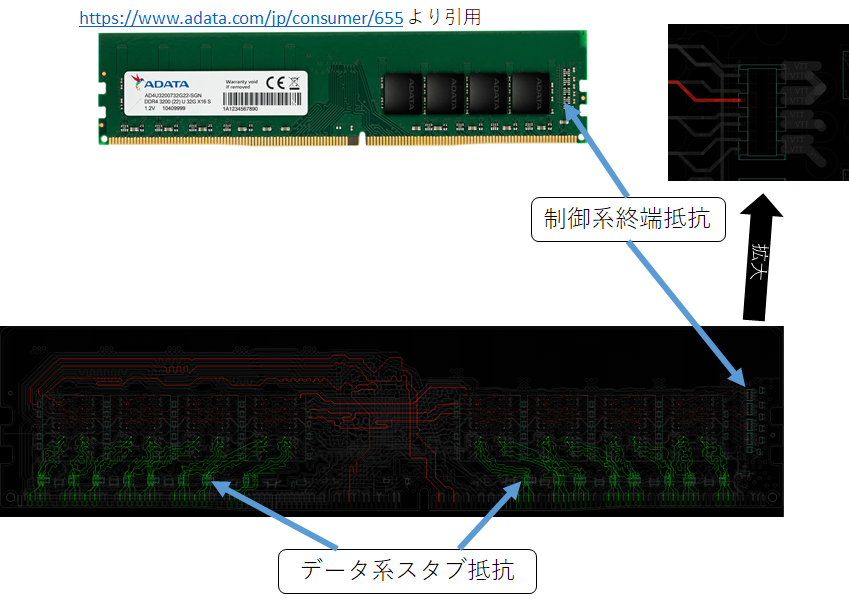
DIMMを眺めるとDRAMチップ以外にも多くの部品が取り付けられていることが分かる。一番大きなのはSPDなのだが、これは話題から離れるのでちょっと置いておいて、数多くついているのが抵抗やコンデンサの類に目を向けよう。これらは端的に言えばノイズ対策のためについている。とりあえず、一部のチップ抵抗にだけ注目しよう。いろんな役目の抵抗があるのだが、今回は制御系とデータ系から1つずつ抜擢する。まずは制御系末端にある終端抵抗だ。

先程の制御系のFly-by Topologyの話で、一本の線からごく短いstubで分岐すれば信号品質を保てるという話をした。確かに「線の途中」に関してはそうだ。だが、一番大事な場所の話をしていない。それは信号線の端っこ、すなわち終端だ。もし終端が短絡していれば抵抗ゼロ相当で反射係数は-1、開放されている、すなわちどこにも繋がっていない場合は抵抗無限大相当で反射係数は1となり、どちらも完全反射となる。インピーダンスマッチングは信号線の末端でこそ最重要になってくるのだ。

それが、DRAMの右の方に付いているチップ抵抗だ。これは終端抵抗(termination resistor)と呼ばれるもので、その抵抗値はよく$R_{TT}$なんて書かれる。アドレス線の場合は33Ωだったりする。詳細はJEDECの設計データに付属のBOM(Bill of Materials,部品表)やSchematicsに書かれている。これは、先程のインピーダンスマッチングにおいて、最初に出した抵抗による終端と同じことで、信号線の端っこに適切な値の抵抗を取り付けることで、電力をきっちりすべて消費し、反射しないようにしてくれるのだ。(なお、信号線の反対側がGNDではなく、VTT(電圧としては電源の半分、目安0.6V)という点でちょっと違うが、ここはスキップさせてもらう。電源周りは https://www.macnica.co.jp/business/semiconductor/articles/texas_instruments/119473/ とかの説明が良いかもしれない。)

ちなみに、データ線にも終端抵抗はあるが、これはODT(On-Die Termination)という形でDRAMチップに内蔵して、その抵抗値を制御できるようにしている。このあたりは下記記事を参考に。

さて、次にピックアップするのはデータ系の信号線の途中についている抵抗だ。例えばDDR信号が流れるDQの抵抗値は15Ωとなっている。データ系信号線の大きな特徴として、メモリコントローラとDRAMチップの両方が信号を駆動し得るというのがある。これは信号反射を抑えるという点から見ると大変厄介だ。ここまでのインピーダンスマッチングの話では、信号線ごとの電源と負荷、すなわちドライバとレシーバーの役割を固定して考えてきた。だが、このDQなどのデータ系信号線はその役割が入れ替わる。分岐のときの特性インピーダンスの話と同様、DRAMチップ側から見たときの信号反射も考えないといけない。分岐単体で見ると信号の向きを変えたときのインピーダンスマッチングを両方成立させることはまず無理だ。(不可能であることの数学的証明はしていないので、若干自信ないが。)

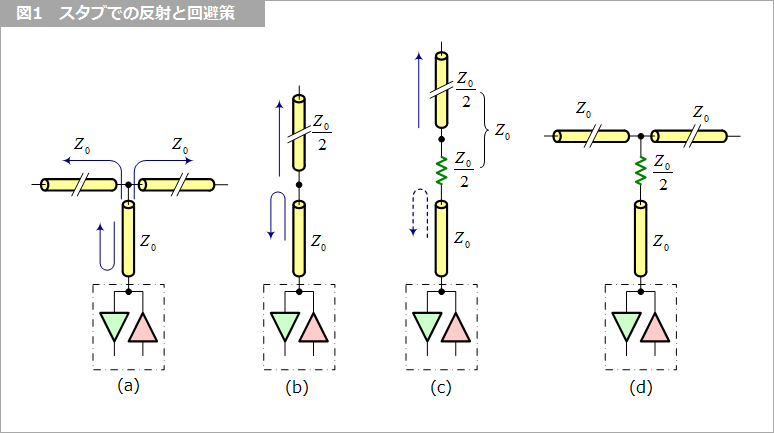
https://www.macnica.co.jp/business/semiconductor/articles/basic/115193/ より引用

そこで、上図の(d)のように分岐のスタブに特性インピーダンスの半分の値の抵抗値を挟み込むと、スタブから見たときのインピーダンスマッチングが取れる。この抵抗をスタブ抵抗とよく呼ぶ。ただ、もちろん信号線を通過したい信号から見るとマッチングは取れてなくて、反射してしまうのだが、それも反射係数1/4程度に抑えることができ、単に分岐するのに比べると信号が改善する。詳細は図の引用元であるマクニカの説明に投げよう。(このあたり、マクニカさんのコラムが有能すぎて俺が書くことがない)

ちなみに、ここで出てくるSSTLは厳密にはDDR3までの方式で、DDR4はPOD(pseudo open-drain)に変わっているが、このあたりのスタブ抵抗のメカニズムは共通だ。

端子部の形状

一昔前に自作PCなどでDIMMをマザーボードに指したことある人は、DIMMの挿入が妙に固くてATX 24-pin 電源コネクタの次ぐらいに難易度が高かったご記憶がある人もいるだろう。DIMMスロットは割と幅(長い方)があり、それを垂直に差し込まないと行けないため、一気に差し込むにはそれなりの力が必要だ。かと言って、精密機器であり、PCBの強度もたかが知れているために、やたらめったら力を入れるわけには行かない。また、DIMMの周辺は込み入っており横から差し込めているのか確認するのが難しいため、DIMMの差し込みが甘く動作不良に陥って原因特定に困った人も要るはずだ。

その点に対して、DDR4には優しさが詰まっている。この端子部の台形状に微妙に長くなってる部分、これはDIMMの挿入圧力を抑える役目がある。DIMMの挿入で力が必要なのは、DIMMの端子がスロットに入り込むその瞬間である。それをDIMMの全端子一気にやるためにその瞬間に大きな力が必要だったのだ。DDR4ではここに長さの違いを設けることで、一気に力を必要とせずに時間的に分散して力をかければ良いようになっている。こんなところにJEDECの愛を感じる人もいるかも知れない(?)。

Part 4の予定

いよいよ次は最後のPart 4である。規格と未来の話とともに、完全に忘れていたデュアルチャンネル(マルチチャンネル)の話を書く予定だ。合わせてランクの話もやる。パソコンやパソコン部品のカタログに書かれている話題がメインになるため、もしかすると一番馴染み深い話かもしれない。だが、ここまでPart 1,2,3と読んだ前後では同じカタログを見たときの解像度が異なるはずだ。

「見えるぞ！私にも電気信号が見える！」(※見えません)

相対論補正を入れて計算したつもりだ。慣れてないので間違ってたら申し訳ない。 ↩
と書いたが、これはあくまで古典論の範疇での話である。実は電磁場とは無関係に電磁ポテンシャルによって電子が影響を受けるアハラノフ・ボーム効果が1986年に実験により確かめられた。かなり最近の出来事であることに驚かれるであろう。物理的な本質は実は電磁ポテンシャルの方にあったのだ。世界は本当に奥深くできているのだ。ただ、詳細はよく知らないので、物理に詳しい諸氏に続きをお願いしよう。 ↩
一般に「電位」とされるのは「静電ポテンシャル」と呼ばれるもので、電場を線積分することによって求まる各点固有の値なのだが、名前通りこれは電磁場が変動しないときの話である。特に磁場の変動がある場合は、単に電場を線積分するだけだと積分経路によって値が異なり、ポテンシャルとして扱うことができない。 ↩
マクスウェル方程式は線形だが、物質中では誘電率や透磁率が変動し、非線形な振る舞いをする。「物質中のマクスウェル方程式」などで調べるとなかなかに激しい話が出てくる。 ↩
言うまでもないが、そんな電源は存在しない。あくまでも理想的な電源だ。 ↩
低周波で本当に無視できるかは、これも回路スケールとの相対的な問題になる。「定在波」などで調べるといろいろ出てくるだろう。 ↩
微妙に真ん中のほうが斜めっているのは、色の都合で見えないが、ピン割当の都合で真ん中の方の端子が電源や制御系の信号線に取られているからである。 ↩
別にこの方式がDDR4で新出というわけではない。あくまでDDR4はこうである、以上の意味はない。 ↩

パソコンユーザーのためのDRAM入門 Part 3 ～限界領域の電磁気～

パソコンユーザーのためのDRAM入門 目次