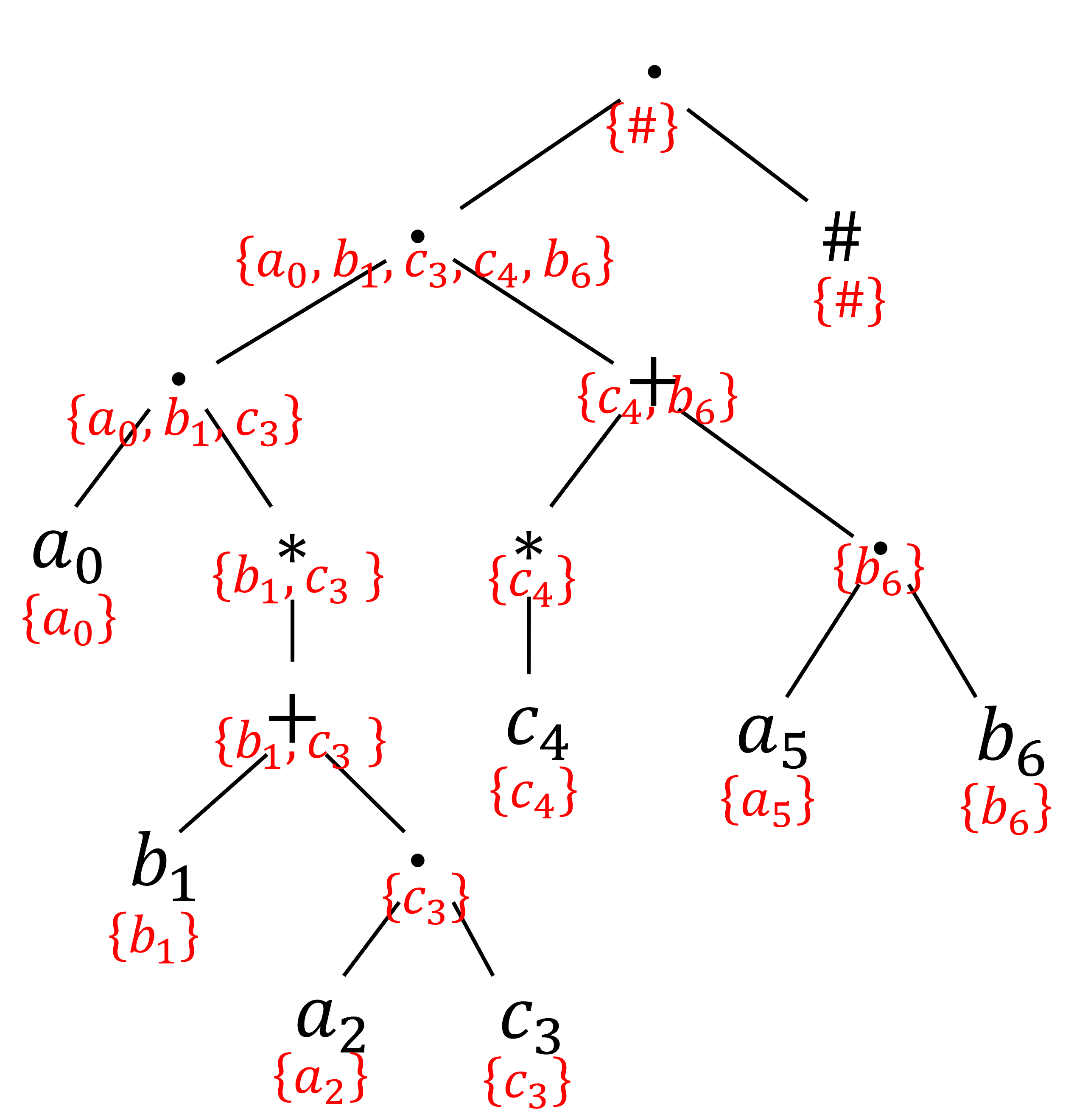本記事では正規表現から決定性有限オートマトンを生成するアルゴリズムについて解説します.
今回紹介するアルゴリズムの実装をhttps://github.com/MikaL-trivial/regex2dfa に置いています.良ければご参照ください.
正規表現とは
ある文字列の集合(言語といいます)を表現する方法の1つです.
例えば$a^*b^*$という正規表現は$\left\lbrace a^i b^j \mid 0 \leq i, j \in \mathbb{Z}_{\geqslant 0} \right\rbrace$という集合,つまり$a$を$0$回以上繰り返した後に$b$を$0$回以上繰り返した文字列の集合を表現しています.
テキストエディタにおいて文字列の検索や置換によく用いられており,様々な演算やメタ文字等が用意されているので,そのあたりの詳しい解説は正規表現入門決定版などを参照していただくとわかりやすいと思います.
本記事で対象とする演算等
今述べた通り正規表現には様々な演算等が用意されているのですが,本記事で対象とするのは以下の基本的なものです.
空列$\varepsilon$が用意されることもありますが,これは$\emptyset^*$と同じ意味なので今回は追加しません.
決定性有限オートマトンとは
そもそもオートマトンとは何かというと,入力された文字列を1文字ずつ読み込んでいき,それに応じて状態を遷移させる機械です.最終的に受理状態という特別な状態にたどり着けばその文字列は受理されるといいます.
オートマトンの中でも特に状態数が有限のものを有限オートマトン,さらに状態遷移が決定的(現在の状態,入力に対して遷移先が1つのみ存在する)である場合に決定性有限オートマトンと呼びます.
こちらの記事「オートマトンと言語」ざっくりまとめが参考になると思います.
本記事でやりたいこと
実は上で紹介した正規表現と決定性有限オートマトンは等価であることが証明されています.
そこで本記事では与えられた正規表現があらわす言語の要素である文字列を受理するような決定性有限オートマトンを生成する過程を見ていきます.
アルゴリズム
以下では例として"$a(b + ac)^*(c^* + ab)$"を取り上げて解説します.
0. 下準備
まず正規表現の末尾を分かりやすくするために特別な文字$\#$を末尾に連接して"$a(b + ac)^*(c^* + ab)\#$"としておきます.以降,末尾に$\#$を連接した正規表現を$e_{\mathrm{root}}$とします.
1. 構文解析
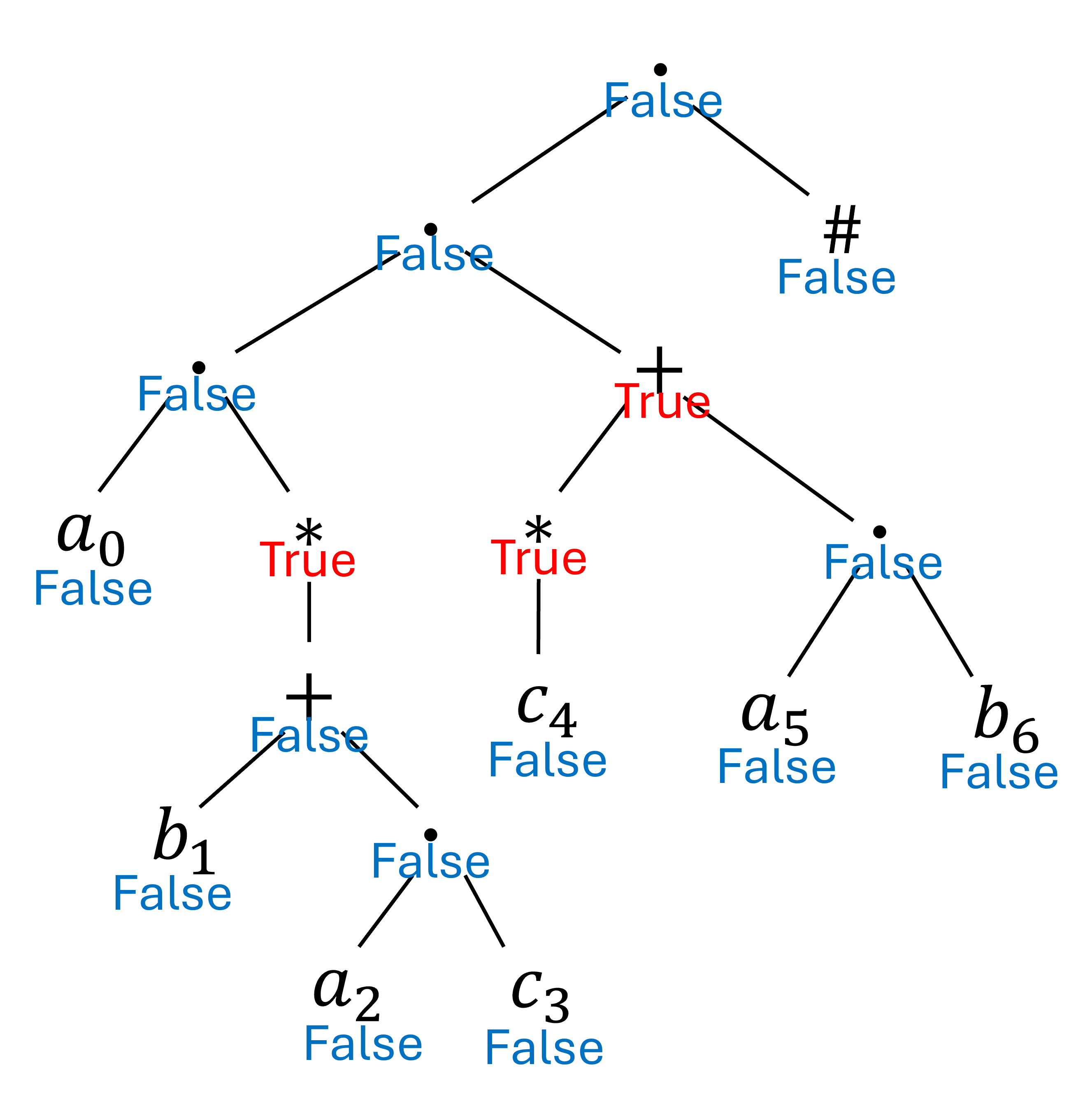
まずは与えられた正規表現を構文解析し,以下のように木構造で表します.

構文解析に用いる文法は以下のようにしました.
\begin{align}
\mathrm{start} &\rightarrow \mathrm{expr} \\
\mathrm{expr} &\rightarrow \mathrm{expr} + \mathrm{term} \\
\mathrm{expr} &\rightarrow \mathrm{term} \\
\mathrm{term} &\rightarrow \mathrm{term} \quad \mathrm{factor} \\
\mathrm{term} &\rightarrow \mathrm{factor} \\
\mathrm{factor} &\rightarrow ( \mathrm{expr} ) \\
\mathrm{factor} &\rightarrow \mathrm{factor}^* \\
\mathrm{factor} &\rightarrow \mathrm{singleton} \\
\mathrm{factor} &\rightarrow \emptyset \\
\mathrm{singleton} &\rightarrow a \dots z|A \dots Z
\end{align}
つまり演算子の優先順位は合併$<$連接$<$クリーネ閉包の順であり,合併・連接は左結合となるように定義しました.また,簡単のために文字としては小文字・大文字のアルファベットのみ採用しています.
実装に関してはLarkというパーサジェネレータを用いました.
詳細な説明についてはPython 構文解析ライブラリLarkを使って簡単な自作言語処理系をつくるなどを参照していただくとよいと思います.
正規表現を構文解析するのにあたって以下のようにlarkファイルを作成しました.
%import common.WS
%import common.LETTER
%ignore WS
?start : expr
?expr : expr "+" term -> union
| term
?term : term factor -> concat
| factor
?factor : "(" expr ")"
| factor "*" -> kleene
| singleton -> singleton
| "\0" -> empty
?singleton : LETTER
2. 各種データの取得
このステップでは与えられた正規表現の各部分表現(例えば$(a + b)^*$に対する$a+b$など)に対して以下のデータを取得します.
- $\mathrm{nullable}(e)$:部分表現$e$は空列$\varepsilon=\emptyset^*$を含んでいるか(ブール値)
- $\mathrm{first}(e)$:部分表現$e$の表す集合の要素の先頭の文字としてありうる文字の集合
- $\mathrm{last}(e)$:部分表現$e$の表す集合の要素の末尾の文字としてありうる文字の集合
- $\mathrm{follow}(a)$:文字$a$の後に続きうる文字の集合
これらは構文解析木の葉の方向から順に計算することにより求めることができます.
計算に際して$e_{\mathrm{root}}$の各文字に対して番号を振っておきます.

2-1. nullableの計算
引数である正規表現が表す集合に空列が含まれるかを示すブール値です.
帰納的に以下のように計算できます.$\newcommand{\F}{\mathrm{False}} \newcommand{\T}{\mathrm{True}}$
- $e$が文字のとき:$\mathrm{nullable}(e) = \F$
- $e = \emptyset$のとき:$\mathrm{nullable}(e) = \F$
- $e = e_1 + e_2$のとき:$\mathrm{nullable}(e) = \mathrm{nullable}(e_1) \lor \mathrm{nullable}(e_2)$
- $e = e_1 e_2$のとき:$\mathrm{nullable}(e) = \mathrm{nullable}(e_1) \land \mathrm{nullable}(e_2)$
- $e = e_1^*$のとき:$\mathrm{nullable}(e) = \T$
2-2. firstの計算
引数である正規表現が表す集合の文字列の先頭の文字になりうる文字の集合です.
以下のように計算できます.
- $e = a$(文字)のとき:$\mathrm{first}(e) = \lbrace a \rbrace$
- $e = \emptyset$のとき:$\mathrm{first}(e) = \emptyset$
- $e = e_1 + e_2$のとき:$\mathrm{first}(e) = \mathrm{first}(e_1) \cup \mathrm{first}(e_2)$
- $e = e_1 e_2$のとき:$\mathrm{nullable}(e_1)$ならば$\mathrm{first}(e) = \mathrm{first}(e_1) \cup \mathrm{first}(e_2)$.そうでなければ$\mathrm{first}(e) = \mathrm{first}(e_1)$
- $e = e_1^*$のとき:$\mathrm{first}(e) = \mathrm{first}(e_1)$
2-3. lastの計算
引数である正規表現が表す集合の文字列の末尾の文字になりうる文字の集合です.
以下のように計算できます.
- $e = a$(文字)のとき:$\mathrm{last}(e) = \lbrace a \rbrace$
- $e = \emptyset$のとき:$\mathrm{last}(e) = \emptyset$
- $e = e_1 + e_2$のとき:$\mathrm{last}(e) = \mathrm{last}(e_1) \cup \mathrm{last}(e_2)$
- $e = e_1 e_2$のとき:$\mathrm{nullable}(e_2)$ならば$\mathrm{last}(e) = \mathrm{last}(e_1) \cup \mathrm{last}(e_2)$.そうでなければ$\mathrm{last}(e) = \mathrm{last}(e_2)$
- $e = e_1^*$のとき:$\mathrm{last}(e) = \mathrm{last}(e_1)$
2-4. followの計算
$e_{\mathrm{root}}$が表す集合内の文字列において,引数である文字の後続になりうる文字の集合です.
以下のように計算します.
- $e = e_1 e_2$のとき:$\mathrm{last}(e_1)$の要素である文字$a$に対して$\mathrm{follow}(a)$に$\mathrm{first}(e_2)$を追加します.
- $e = e_1^*$のとき:$\mathrm{last}(e_1)$の要素である文字$a$に対して$\mathrm{follow}(a)$に$\mathrm{first}(e_1)$を追加します.
その他の場合は特に操作を行いません.
例の場合は以下のようになります.
| 文字 | $\mathrm{follow}$ |
|---|---|
| $a_0$ | $\lbrace b_1, a_2, c_4, a_5, \# \rbrace$ |
| $b_1$ | $\lbrace b_1, a_2, c_4, a_5, \# \rbrace$ |
| $a_2$ | $\lbrace c_3 \rbrace$ |
| $c_3$ | $\lbrace b_1, a_2, c_4, a_5, \# \rbrace$ |
| $c_4$ | $\lbrace c_4, \# \rbrace$ |
| $a_5$ | $\lbrace b_6 \rbrace$ |
| $b_6$ | $\lbrace \# \rbrace$ |
| $\#$ | $\emptyset$ |
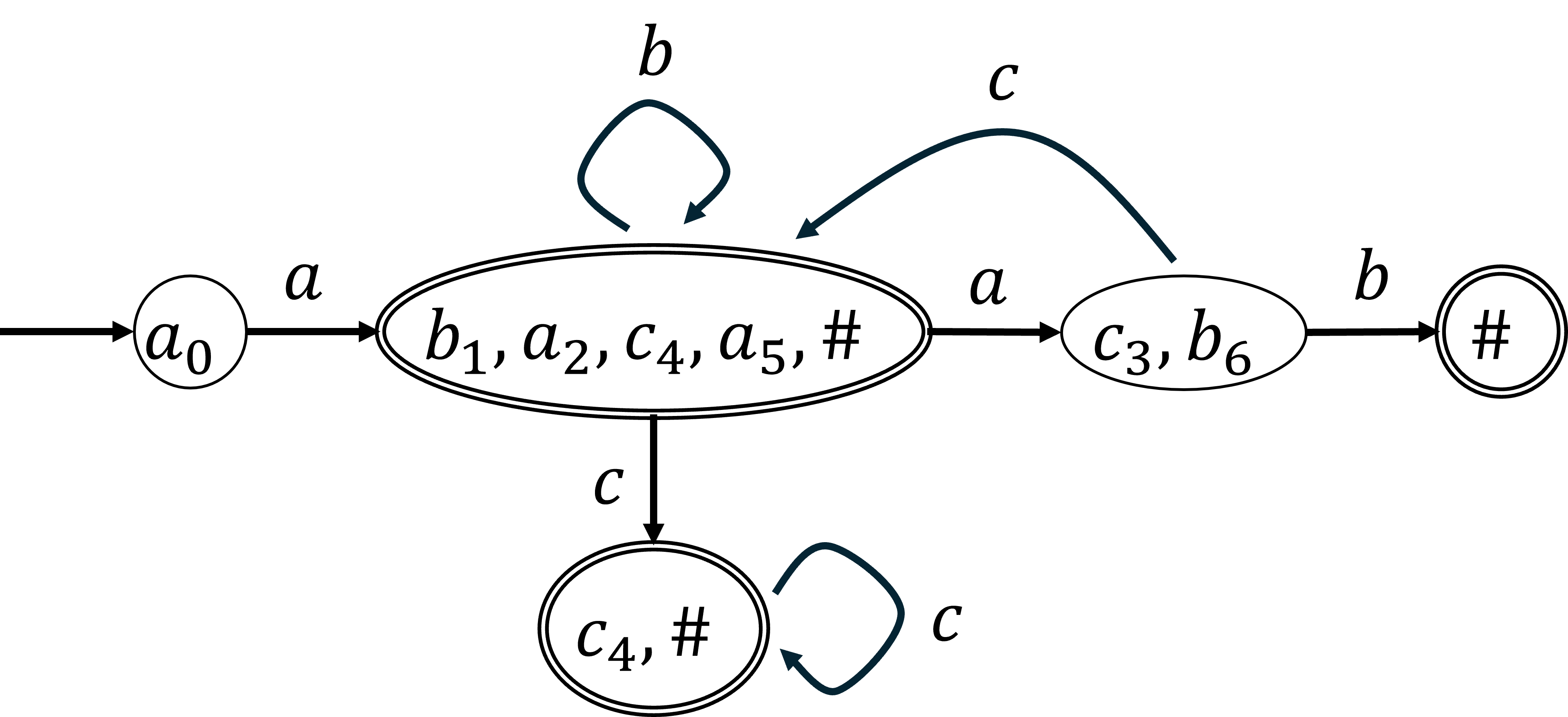
3. オートマトンの構成
集めたデータをもとにオートマトンを構成していきます.
- 始状態:$\mathrm{first}(e_{\mathrm{root}})$
- 受理状態:$\#$を含む集合
- 状態遷移:ある状態$Q$中にある文字$a$が$a_{i_1}, a_{i_2}, \dots, a_{i_n}$のように含まれているとき,$a$を入力したときの次の状態を$\mathrm{follow}(a_{i_1}) \cup \mathrm{follow}(a_{i_2}) \cup \dots \cup \mathrm{follow}(a_{i_n})$とします.
遷移関数を全域的(すべての状態,すべての文字に対して遷移先の状態が存在する)にしたい場合は状態を1つ追加し,存在しない遷移の代わりにその状態への遷移を作ればよいです.
アルゴリズムの気持ち
オートマトンの各状態は文字の集合になっていましたが,これは直感的には「受理状態に至るために入力してほしい文字の集合」を表しています.
例の場合,最初は$a$から入力しなければ受理されないので始状態が$\lbrace a_0 \rbrace$となっています.
また,$\#$が含まれていれば受理状態になるのは,$\#$は末尾を表すためにこれ以上文字を入力する必要がないからと考えることができます.
遷移関数に$\mathrm{follow}$を用いたのは,ある文字を入力した後に受理状態に至るにはその後続の文字を入力してほしいからですね.
最後に
本記事で紹介したアルゴリズムをPythonで実装したコードをhttps://github.com/MikaL-trivial/regex2dfa にあげています.
拙くはありますが実装の際の参考にしていただけると幸いです.
また,本記事内に誤り等があった場合はコメントでご指摘ください.