「計算理論の基礎(1) オートマトンと言語」を読んだので、ざっくりまとめ。
ざっくりまとめなので、証明とかを特にしません。
第1章 正規言語
有限オートマトン
有限オートマトンは有限状態機械とも呼ばれるモデルである。計算機がある入力を受理、または拒否するかを表現するモデルである。
有限オートマトンは状態遷移図によって表現される。
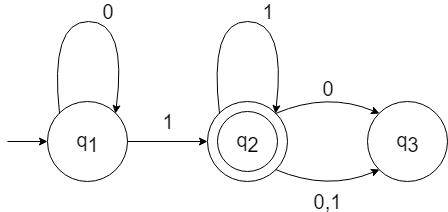
$M_1$は0または1をアルファベット(入力可能な文字)とする有限オートマトンである。
$q_1$、$q_2$、$q_3$は状態であり、状態から状態への矢印は遷移である。
何もないところからの矢印がある$q_1$は開始状態であり、2重円の$q_2$は受理状態である。
有限オートマトンが入力を受け取ると、開始状態から始動し、1つ1つ読みだした文字に沿ってそのラベルのある遷移に従って状態から状態へ移動する。
すべての入力を読み終えたときに受理状態にあればその入力を受理する。
受理状態ではない状態にあれば入力を拒否する。
例えば、1101という入力に対して$M_1$は開始状態($q_1)$から始動し、
q_1 \xrightarrow{ 1 } q_2 \xrightarrow{ 1 } q_2 \xrightarrow{ 0 } q_3 \xrightarrow{ 1 } q_2
と遷移し、$q_2$は受理状態なので$M_1$は入力1101を受理する。
非決定性有限オートマトン
$M_1$は状態と文字によって次に遷移する状態が一意に決まっている。
これを決定性計算と呼び、そのような有限オートマトンを**決定性有限オートマトン(deterministic finite automaton)**と呼ぶ。DFAと略す。
これに対し、状態と文字によって次の状態への遷移が複数ある場合や文字の入力なし(εで表す)の遷移が存在する場合、**非決定性有限オートマトン(nondeterministic finite automaton)**と呼ぶ。NFAと略す。
NFAでは、遷移先が複数あるような場合にその時点でその個数分だけコピーを作成し、それぞれのコピーが処理を継続する。
そのうちの一つでも受理状態になれば、NFAは入力を受理する。
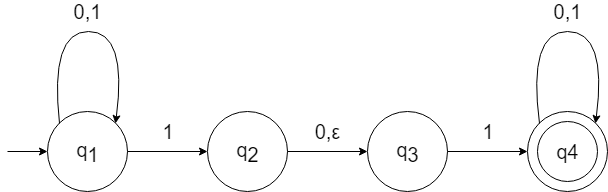
$N_1$は非決定性有限オートマトンである。
状態遷移図を見ると、$q_1$の状態で文字1を読み取ると$q_1$または$q_2$に遷移する。
これは処理的には$q_1$に遷移した状態と$q_2$に遷移した状態のそれぞれのコピーが作られて処理が進む。
また、$q_2$から$q_3$に移動するためのラベルにεがある。
これは、文字を読み取ることなく$q_2$から$q_3$に遷移できることを示しているため、$q_1$の状態で1を読み取った場合の遷移先としては、$q_1$、$q_2$、$q_3$の3状態になる可能性がある。
DFAとNFAは同じ言語クラスを認識する。
つまり、すべてのNFAから同じ言語を認識するDFAに変換することができる。
2つの機械が同じ言語を認識するとき、等価であるという。
正規言語
有限オートマトンが認識できる言語を正規言語と呼ぶ。
正規演算
正規言語に関する以下の正規演算を定義する。
- 和集合演算:$A \cup B = \{x\ |\ x \in A または x \in B\}$
-
連結演算:$A \circ B = \{xy\ |\ x \in
A かつ y \in B \}$ - スター演算:$A^* = \{x_1x_2 \dots x_k \ |\ k \geq 0 かつ、各々のx_iに対してx_i \in A\}$
和集合演算はAとBにあるすべての文字列の和集合を新しい言語の文字列とする演算である。
連結演算はAの文字列の後にBの文字列が続くようなすべての組み合わせの文字列を新しい言語の文字列とする演算である。
スター演算は単項演算であり、Aの文字列を任意個連結したものを新しい言語の文字列とする演算である。ここで、「任意個」には0個も含まれるため、εは$A^*$の要素となる。
これらの演算は3つとも正規言語クラスで閉じている。
すなわち、正規言語に対してこれらの演算を行った結果も正規言語となる。
正規表現
正規演算を用いて言語を記述する表現を正規表現である。
正規表現と有限オートマトンは記述能力において等価である。
第2章 文脈自由言語
文脈自由文法
正規表現では$\{0^n1^n| n \geq 0\}$のような言語を記述することができない。
文脈自由文法は再帰的な構造を記述可能で、正規表現よりも強力な表現力を持つ。
A \rightarrow 0A1 \\
A \rightarrow B \\
B \rightarrow ε
文脈自由文法$G_1$
$G_1$は前述した$\{0^n1^n\ |\ n \geq 0\}$という言語を表現するための文脈自由文法である。
文法は生成規則(書き換え規則)の集まりからなる。
生成規則の矢印の左辺には変数、右辺には変数と終端記号が現れる。
いずれかの変数が開始変数として指定される(先頭規則の左辺の変数や変数$S$(start)がよくつかわれる)。
文法から文字列を生成するためには開始変数から始め、現在の状態に含まれる変数をその変数を左辺とする生成規則の右辺で書き換えるという処理を変数がなくなるまで繰り返す。
例えば、$G_1$で000111を生成する過程は以下のようになる。
A \Rightarrow 0A1 \Rightarrow 00A11 \Rightarrow 000B111 \Rightarrow 000111
$G_1$にはAから生成される規則が2つあるが、そのような場合はどちらを選んでもよい。
また、そのような場合に「or」を表す記号「|」を使って、$A \rightarrow 0A1\ |\ B$のように略記する。
文脈自由文法から生成される言語を文脈自由言語と呼ぶ。
プッシュダウン・オートマトン
プッシュダウン・オートマトン(PDA)は非決定性有限オートマトンにスタックが構成要素として追加されたものであり、文脈自由言語を認識することができる。
スタックは文字を記憶(プッシュ)する場合は先頭にデータを追加し、文字を取り出す(ポップ)する場合は先頭から文字を取り出す「後入先出(last in, first out)」の記憶装置である。
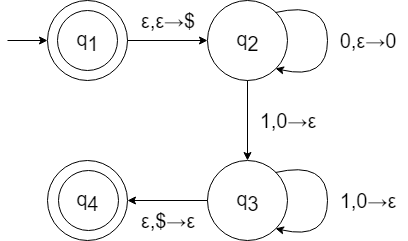
$\{0^n1^n\ |\ n \geq 0\}$を認識するPDA $M_2$の状態遷移図
PDAの場合の状態遷移図は入力文字とスタックに対する操作を遷移に記述する。
「$a,b→c$」のように記述した場合、入力$a$を読み出し、スタックの先頭文字$b$を$c$で置き換えるという意味になる。
$b$がεのときはスタックへのプッシュのみ、$c$がεのときはスタックからのポップのみで状態の遷移を行う。
$M_2$では、$q_1$から$q_2$に読み出しなしで$を文字としてスタックに追加する。
その後、0を読み出すたびに0をプッシュしていき($q_2$ → $q_2$)、1が読み出されたら0をポップし、$q_3$に遷移する。
$q_3$では、1を読み出すたびに1をプッシュしていく($q_3$ → $q_3$)。
$q_4$への遷移は$をポップして遷移するが、最初に追加した文字$をポップするということはスタックが空になっているということなので、0と1が同数の場合に受理する。