今回は深層学習編です。
解答は白文字で記入しているので、文字を選択すれば見れます。
数学はこちら
https://qiita.com/MeiByeleth/items/e71c631185cd5d39a705
機械学習はこちら
https://qiita.com/MeiByeleth/items/2fac526bbcab07ece4d7
順伝番ネットワーク
線形問題と非線形問題
1.
次の選択肢からパーセプトロンで解けないものを選べ。
(1)XORゲート
(2)ANDゲート
(3)ORゲート
(4)NANDゲート
解答:1
コスト関数
1.
次の選択肢から正しい記述を選べ。
(1)NNのコスト関数には二乗誤差が用いられる。
(2)クロスエントロピーは計算が複雑なのであまり用いられない。
(3)コスト関数は計算の速さも求められる。
(4)クロスエントロピーは正解と間違っているとペナルティが二乗誤差より小さく、正解に近いと大きくなる。
解答:3
出力ユニット
1.
次の選択肢から出力ユニットでないものを選べ。
(1)RelUユニット
(2)Sigmoidユニット
(3)Softmaxユニット
(4)線形ユニット
解答:1
2.
次の選択肢からソフトマックスの出力$y_k$として正しいものを選べ。ただし$y_1+y_2+\cdots + y_N=1$とする。
(1)$y_k=\frac{(x_k)}{\sum_{j=1}^{N}(x_j)}$
(2)$y_k=\frac{exp(x_k)}{\sum_{j=1}^{N}exp(x_j)}$
(3)$y_k=\frac{log(x_k)}{\sum_{j=1}^{N}log(x_j)}$
(4)$y_k=\frac{(x_k)^2}{\sum_{j=1}^{N}(x_j)^2}$
解答:2
隠れユニット
1.
次の選択肢から隠れユニットの説明として誤ったものを選べ。
(1)RelUユニット
(2)Sigmoidユニット
(3)Softmaxユニット
(4)線形ユニット
解答:1
2.
次の選択肢からソフトマックスの出力$y_k$として正しい数式を選べ。ただし$y_1+y_2+\cdots + y_N=1$とする。
(1)$y_k=\frac{(x_k)}{\sum_{j=1}^{N}(x_j)}$
(2)$y_k=\frac{exp(x_k)}{\sum_{j=1}^{N}exp(x_j)}$
(3)$y_k=\frac{log(x_k)}{\sum_{j=1}^{N}log(x_j)}$
(4)$y_k=\frac{(x_k)^2}{\sum_{j=1}^{N}(x_j)^2}$
解答:2
アーキテクチャの設計
1.
次の選択肢は万能近似定理に関する記述である。(a)に当てはまる語句を次の選択肢から選べ。
定数でない連続な有界単調増加の関数を(a)層以上のNNは任意の連続関数を任意の精度で表現可能である。
(1)2
(2)3
(3)4
(4)5
解答:2
誤差伝播およびその他のアルゴリズム
1.
RelUレイヤを実装したい。(a)に当てはまるコードを選べ。
import numpy as np
class Relu:
def __init__(self):
self.mask=None
def forward(self,x):
self.mask=(x>0)
out=x if self.mask else 0
return out
def backward(self, dout):
(a)
return dx
(1)dx=dout
(2)dx=1-dout if self.mask else 0
(3)dx=1/np.exp(dout) if self.mask else 0
(4)dx=dout if self.mask else 0
解答:4
2.
sigmoidレイヤを実装したい。(a),(b)に当てはまるコードを選べ
class Sigmoid:
def __init__(self):
self.out=None
def forward(self,x):
(a)
self.out=out
return out
def backward(self,dout):
dx = dout*(1.0-self.out)*self.out
return dx
(a):
(1)out=1/(1+np.exp(-x))
(2)out=1/(1+np.exp(+x))
(3)out=1/(1-np.exp(-x))
(4)out=1/(1-np.exp(+x))
解答:1
(b):
(1)dx = dout
(2)dx = dout*(1.0-self.out^2)
(3)dx = dout*(1.0+self.out)*self.out
(4)dx = dout*(1.0-self.out)*self.out
解答:4
3.
次の選択肢の中からソフトマックスにおける交差エントロピーの式を選べ。ただし、$y_k$をNNの出力、$t_k$を正解ラベルとする
(1)$E=- \sum_k y_{k}log~t_{k}$
(2)$E=- \sum_k (y_{k}log~t_{k}+(1-y_{k})log~(1-t_{k}))$
(3)$E=- \sum_k t_{k}log~y_{k}$
(4)$E=- \sum_k( t_{k}log~y_{k}+(1-t_{k})log~(1-y_{k}))$
解答:3
4.
Softmaxレイヤーを実装したい。(a)(b)に入るコードを選べ。
import numpy as np
def softmax(x):
max_x=max(x)
sum_x=sum(np.exp(x-max_x))
ex_x=np.exp(x-max_x)
ex_x/=sum_x
return ex_x
def cross_entropy(t,y):
delta=1e-7
return (a)
class softmax_with_loss:
def __init__(self):
self.loss=None#損失
self.y=None #softmaxの出力
self.t=None #教師データ
def forward(self,x,t):
self.t=t
self.y=softmax(x)
self.loss=cross_entropy(self.t,self.y)
return self.loss
def backward(self, dout=1):
batch_size=self.t.shape[0]
dx=(b)
return dx
(a)
(1)-sum(t*np.log(y+delta))
(2)-sum(y*np.log(t+delta))
(3)-sum(t*np.log(y+delta)+(1-t)*np.log(1-y+delta))
(4)-sum(y*np.log(t+delta)+(1-y)*np.log(1-t+delta))
解答:1
(b)
(1)self.y-self.t
(2)self.t*np.log(self.y+delta)
(3)(self.t*np.log(self.y+delta))/batch_size
(4)(self.y-self.t)/batch_size
解答:4
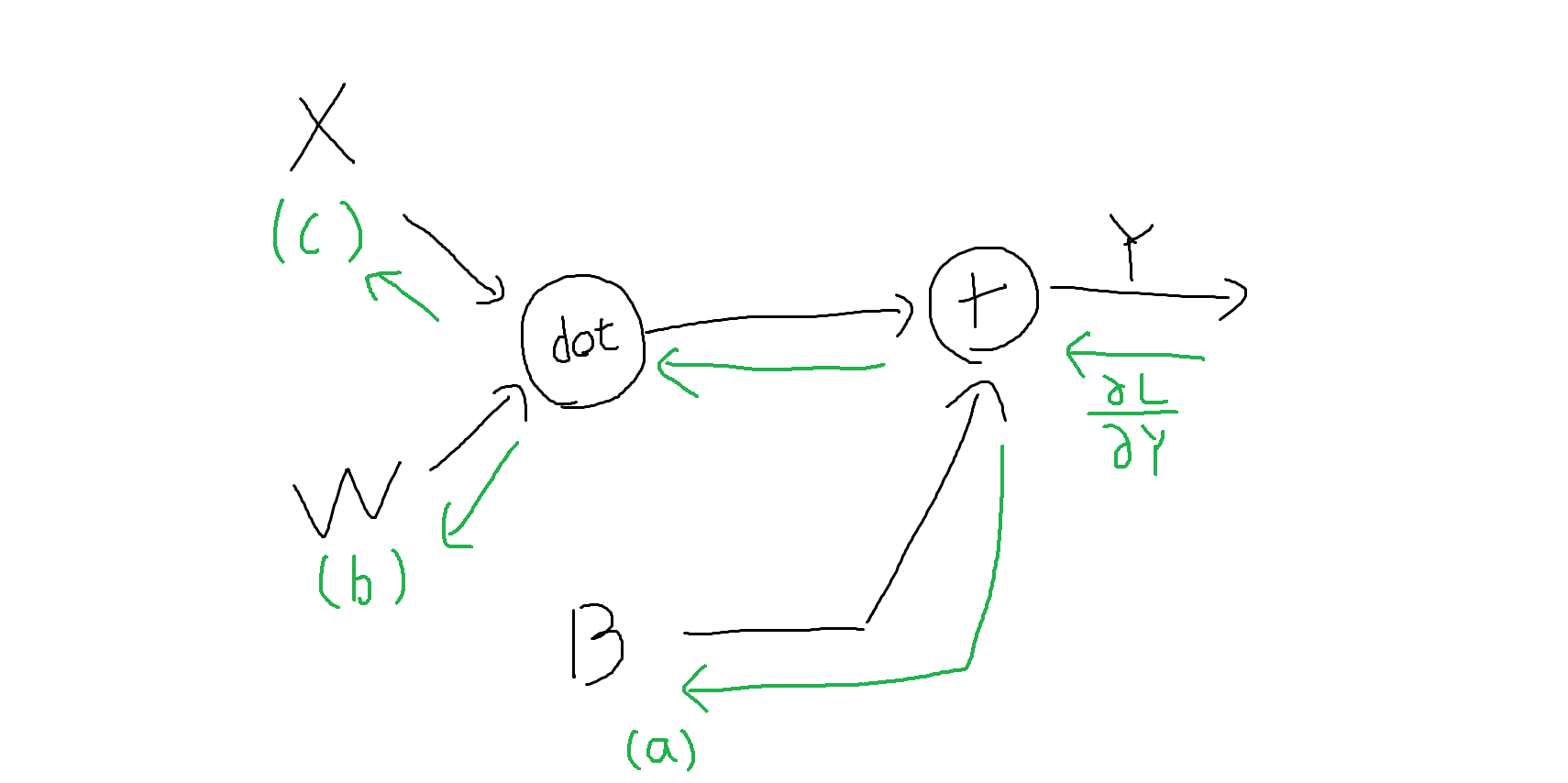
5.
$X$を3次元の配列、$W$を3行4列の行列,$B$を4次元の配列とする。逆伝播させた際の$\frac{\partial L}{\partial B}$(図の(a))、$\frac{\partial L}{\partial W}$(図の(b))、$\frac{\partial L}{\partial X}$(図の(c))の値を次の選択肢から選べ。
(a)
(1)$\frac{\partial L}{\partial B}=\frac{\partial L}{\partial Y}$
(2)$\frac{\partial L}{\partial B}=\frac{\partial L}{\partial Y}(W\cdot X)$
(3)$\frac{\partial L}{\partial B}=\frac{\partial L}{\partial Y}W$
(4)$\frac{\partial L}{\partial B}=Y$
解答:1
(b)
(1)$\frac{\partial L}{\partial W}=\frac{\partial L}{\partial Y}$
(2)$\frac{\partial L}{\partial W}= \frac{\partial L}{\partial Y}\cdot X$
(3)$\frac{\partial L}{\partial W}=X^T\cdot \frac{\partial L}{\partial Y}$
(4)$\frac{\partial L}{\partial W}=W^T\cdot \frac{\partial L}{\partial Y}$
解答:3
(c)
(1)$\frac{\partial L}{\partial X}=\frac{\partial L}{\partial Y}$
(2)$\frac{\partial L}{\partial X}=\frac{\partial L}{\partial Y}\cdot W^T$
(3)$\frac{\partial L}{\partial X}=\frac{\partial L}{\partial Y}\cdot X$
(4)$\frac{\partial L}{\partial X}=W^T\cdot \frac{\partial L}{\partial Y}$
解答:2
深層モデルのための正則化
1.
次の選択肢から誤った記述を選べ。
(1)L1,L2正則化はどちらも過学習の抑制が見込まれる。
(2)L1正則化項は、正則化パラメータと重みのノルムを掛け合わせたものを指す。
(3)L2正則化項により重みがスパースになるので計算コストの低減が望まれる。
(4)L2正則化項を用いた回帰をリッジ回帰という。
解答:3
2.
次の選択肢から誤った記述を選べ。
(1)学習データが多いと過学習しにくくなる。
(2)画像の学習データを増やす場合、左右反転、上下反転、色の変換などがあげられる。
(3)学習データを増やす際、ドメイン固有知識が必要である。
(4)文章の学習データを増やす手法はまだ見つかっていない。
解答:4
3.
次の選択肢から正しい記述を選べ。
(1)半教師あり学習とは教師ラベルがついていないデータに、教師ラベルがついているデータからラベルを付けて学習する手法である。
(2)マルチタスク学習とは複数の問題を複数のネットワークで同時に解く手法である。
(3)Dropoutはネットワークの中で一部のノードを一時的に無効化する手法であり、学習ごとに無効化するノードは変えない手法である。
(4)早期終了とは訓練誤差が上昇する前に学習を止める手法である。
解答:1
4.
次の選択肢からアンサンブル学習でない手法を選べ。
(1)勾配ブースティング
(2)ランダムフォレスト
(3)決定木
(4)スタッキング
解答:3
5.
次の中からDeepLearningで主に用いられる学習手法を選べ。
(1)バッチ学習
(2)ミニバッチ学習
(3)オンライン学習
解答:2
深層モデルのための最適化
パラメータの初期化戦略
1.
次の選択肢から誤った記述を選べ。
(1)Xavierの初期化はx=0の点において点対称の活性化関数に用いられる。
(2)Heの初期化はx=0の線において線対称の活性化関数に用いられる。
(3)初期値によって重みが局所最適解に陥る場合がある。
(4)tanhは点対称の活性化関数である。
解答:2
基本的なアルゴリズム
1.
Momentumの数式を次の選択肢の中から選べ。ただしLは損失関数、Wは重み、$\alpha$は減衰率、$\eta$は学習係数とする。
(1)
$\nu←\alpha\nu-\eta\frac{\partial L}{\partial W}$
$W←W-\nu $
(2)
$\nu←\alpha\nu-\eta\frac{\partial L}{\partial W}$
$W←W+\nu $
(3)
$\nu←\alpha\nu+\eta\frac{\partial L}{\partial W}$
$W←W-\nu $
(4)
$\nu←\alpha\nu+\eta\frac{\partial L}{\partial W}$
$W←W+\nu $
解答:2
2.
AdaGradの数式を次の選択肢の中から選べ。ただしLは損失関数、Wは重み、$\eta$は学習係数、⦿は行列の要素ごとの掛け算とする。
(1)
$h←h+\frac{1}{\sqrt h}(\frac{\partial L}{\partial W}⦿\frac{\partial L}{\partial W})$
$W←W-\eta \frac{\partial L}{\partial W} $
(2)
$h←h+\frac{\partial L}{\partial W}$
$W←W-\eta \frac{1}{\sqrt h} \frac{\partial L}{\partial W} $
(3)
$h←h+\frac{\partial L}{\partial W}⦿\frac{\partial L}{\partial W}$
$W←W-\eta \frac{1}{\sqrt h} \frac{\partial L}{\partial W} $
(4)
$h←h+\eta(\frac{\partial L}{\partial W}⦿\frac{\partial L}{\partial W})$
$W←W- \frac{1}{\sqrt h} \frac{\partial L}{\partial W} $
解答:3
3.
RMSPropの数式を次の選択肢の中から選べ。ただしLは損失関数、Wは重み、$\beta$は減衰率、$\eta$は学習係数、$\epsilon$は限りなく0に近い値、⦿は行列の要素ごとの掛け算とする。
(1)
$ v ← \beta v + (1-\beta)|\frac{\partial L}{\partial W} | $
$ w ← w - \frac{\eta}{\sqrt{v}+\epsilon} \frac{\partial L}{\partial W} $
(2)
$ v ← \beta v + (1-\beta)(\frac{\partial L}{\partial W} ⦿ \frac{\partial L}{\partial W}) $
$ w ← w - \frac{\eta}{\sqrt{v}+\epsilon} \frac{\partial L}{\partial W} $
(3)
$ v ← \beta v + (1-\beta)(\frac{\partial L}{\partial W} ⦿ \frac{\partial L}{\partial W}) $
$ w ← w + \frac{\eta}{\sqrt{v}+\epsilon} \frac{\partial L}{\partial W} $
(4)
$ v ← \beta v + (1-\beta)(\frac{\partial L}{\partial W} ⦿ \frac{\partial L}{\partial W}) $
$ w ← w - \frac{\eta}{\sqrt{v}+\epsilon} $
解答:2
4.
下記にAdamの数式を示す、(a)に当てはまる式を選択肢の中から選べ。ただしLは損失関数、Wは重み、$\beta_1$,$\beta_2$は減衰率、$\epsilon$は限りなく0に近い値、⦿は行列の要素ごとの掛け算とする。
{\begin{align}
& m' ← \beta_1 m + (1-\beta_1)\frac{\partial L}{\partial W} \\
& v'← \beta_2 v+ (1-\beta_2)(\frac{\partial L}{\partial W} ⦿ \frac{\partial L}{\partial W}) \\
& m ← \frac{m'}{1-\beta_1} \\
& v ← \frac{v'}{1-\beta_2} \\
& (a)
\end{align}
}
(1)$w ← w - \frac{\eta}{\sqrt{v}+\epsilon} m$
(2)$w ← w - \frac{v}{\sqrt{\eta}+\epsilon} m$
(3)$w ← w - \frac{v}{{\eta}+\epsilon} m$
(4)$w ← w - \frac{\sqrt v}{{\eta}+\epsilon} m$
解答:1
5.
momentumのコードを完成させたい。(a)に当てはまるコードを選べ。
class Momentum:
def __init__(self, lr=0.01, momentum=0.9):
self.lr = lr
self.momentum = momentum
self.v = None
def update(self, params, grads):
if self.v is None:
self.v = {}
for key, val in params.items():
self.v[key] = np.zeros_like(val)
for key in params.keys():
(a)
(1)
self.v[key] = self.momentum*self.v[key] + self.lr*grads[key]
params[key] -= self.v[key]
(2)
self.v[key] = self.momentum*self.v[key] + self.lr*grads[key]
params[key] -= self.momentum
(3)
self.v[key] = self.lr*self.v[key] + self.momentum*grads[key]
params[key] += self.v[key]
(4)
self.v[key] = self.lr*self.v[key] + self.momentum*grads[key]
params[key] += self.momentum
解答:1
最適化戦略とメタアルゴリズム
1.
次の選択肢から正しい記述を選べ。
(1)Batch Normalizationはバッチサイズに関係なく使用できる。
(2)各チャンネル独立に画像の縦横方向についてのみ平均・分散を取る手法をLayer Normalizationと言う。
(3)バッチサイズが十分に確保できない場合の対策として、全チャンネルに跨って平均・分散をとるのがInstance Normalizationである。
(4)Batch Normalizationのバッチサイズが1の場合、Instance Normalizationと等価である。
解答:4
畳み込みニューラルネットワーク
1.
次のうち畳み込みニューラルネットワークについて誤った記述を選べ。
(1)Poolingによって画像の並進移動にロバストになる。
(2)パラメータ共有によって転移学習が容易になる。
(3)Dilated Convolutionは入力に0を埋めて拡大後畳み込む処理であり、セマンティックセグメンテーションに用いられる。
(4)im2colはGPUで効率よく計算できる手法である。
解答:3
2.
h:畳み込む前の画像の高さ
w:畳み込む前の画像の横幅
k:フィルタサイズ
p:パディングのサイズ
s:ストライドの幅
としたとき、
h':畳み込んだ後の画像の高さ
w':畳み込んだ後の画像の横幅
を表す式を次の選択肢の中から選べ。
(1)
$h'=\frac{(h+2p-k)}{s}+1$
$w'=\frac{(w+2p-k)}{s}+1$
(2)
$h'=\frac{(h+2p-k)}{2}+s$
$w'=\frac{(w+2p-k)}{2}+s$
(2)
$h'=\frac{(h+p-k)}{s}+1$
$w'=\frac{(w+p-k)}{s}+1$
(4)
$h'=\frac{(h+p-k)}{k}+s$
$w'=\frac{(w+p-k)}{k}+s$
解答:1
回帰結合型ニューラルネットワークと再帰的ネットワーク
1.
次の選択肢からRNNについての正しい記述を選べ。
(1)誤差逆伝播法をする手法がない。
(2)並列計算が可能である。
(3)スキップ接続によりパラメータを減らせる。
(4)勾配消失、勾配発散の問題がある。
解答:4
2.
下記はLSTMの初期化をするコードである。wは重み、bはバイアスを示す。
n_input = 32
n_hidden = 64
w =np.random.randn((a))
b =np.random.randn((b))
def lstm(x, h, c):
z = ...i = ...f = ...o = ...
このとき(a)と(b)に当てはまるコードを選べ。
(a)
(1)n_inputs+n_hidden,n_hidden4
(2)n_inputs+n_hidden,n_hidden3
(3)n_hidden,n_hidden*4
(4)n_inputs,n_hidden
解答:1
(b)
(1)n_inputs+n_hidden
(2)n_hidden3
(3)n_hidden4
(4)n_hidden
解答:3
3.
GRUのメリットとして正しいものを選べ。
(1)更新ゲートと入力ゲートの2つから構成されており、メモリセルが排除できた。
(2)入力重み衝突を回避できる。
(3)誤差が伝播しにくいので学習が安定する。
(4)勾配消失が起きにくい。
解答:1
生成モデル
識別モデルと生成モデル
1.
ナイーブベイズは生成モデルか。
(1)はい
(2)いいえ
解答:1
オートエンコーダー
1.
オートエンコーダーの特徴でないものを選べ。
(1)入力と同じ出力である
(2)再構成ロスを使う。
(3)識別モデルである。
(4)隠れ層は入力出力層より少なくする。
解答:3
2.
VAEをKLダイバージェンスでなくJSダイバージェンスに変更するとどうなるか。次の選択肢の中から選べ。
(1)変化なし。
(2)計算が早くなる。
(3)画像の輪郭がぼやけにくくなる。
(4)上記に回答はない。
解答:3
3.
VAEの損失関数を次の選択肢の中から選べ。Yは出力、Xは入力、βはハイパーパラメータとする。
(1)$h= D_{KL}[N(\mu (x),\sum(x))||N(0,1)]+\beta||Y-X|| $
(1)$h= D_{KL}[N(\mu (x),\sum(x))||N(0,1)]+\beta||Y-X||^2 $
(1)$h= D_{KL}[N(\mu (x),\sum(x))||N(\mu,1)]+\beta||Y-X|| $
(1)$h= D_{KL}[N(\mu (x),\sum(x))||N(\mu ,1)]+\beta||Y-X||^2 $
解答:2
GAN
1.
D(x):入力データが学習データからきている確率(D(x)=1:学習データ、D(x)=0:Gから生成したデータ)
P(x):任意の分布
x∼pdata(x):学習データの分布に従うデータ
x∼px(x):Gから生成された出力の分布に従うデータ
E(x):期待値
としたときにGANの損失関数を次の選択肢の中から選べ。
(1)$max_G~min_DC(D,G)=E_{x\sim pdata(x)}[logD(x)]+E_{x\sim px(x)}[log(1-D(G(z)))]$
(2)$max_G~min_DC(D,G)=E_{x\sim pdata(x)}[log(1-D(G(z)))]+E_{x\sim px(x)}[logD(x)]$
(3)$min_G~max_DC(D,G)=E_{x\sim pdata(x)}[logD(x)]+E_{x\sim px(x)}[log(1-D(G(z)))]$
(4)$min_G~max_DC(D,G)=E_{x\sim pdata(x)}[log(1-D(G(z)))]+E_{x\sim px(x)}[logD(x)]$
解答:3
2.
DCGANに用いられないものを次の選択肢の中から選べ。
(1)全結合層
(2)global average pooling
(3)Batch Normalization
(4)Leaky ReLU
解答:1
3.
Conditional GANは半教師あり学習か。
(1)はい
(2)いいえ
解答:1</font>
強化学習
1.
次の中からSARSAの更新式を次の選択肢の中から選べ。
(1)
Q^\pi(s,a)←r(s,a)+\gamma \sum_{s'}p(s'|s,a)V^\pi(s')
(2)
Q(s,a)←Q(s,a)+\alpha(R(s,a)+ \gamma Q(s',a')-Q(s,a))
(3)
Q(s,a)←Q(s,a)+\alpha(R(s,a)+ \gamma max_{a'}E[Q(s',a')]-Q(s,a))
(4)
Q(s,a)←Q(s,a)+\alpha(R(s,a)+ \gamma max_{a'}E[Q(s',a')]+Q(s,a))
解答:2
2.
次の選択肢から正しい記述を次の選択肢の中から選べ。
(1)AlphaGOはランダムフォレストをベースにした手法で、PolicyNetworkとValueNetworkの2つのネットワークを持つ。
(2)Distributional RLはネットワークにノイズを載せる手法である。
(3)Fixed TargetはQの値をミニバッチごとの更新が終わる前に重みを更新する手法である。
(4)Double DQNは状態価値ネットワークと行動選択ネットワークを分ける手法である。
解答:4
3.
次の中から強化学習の要素でないものを次の選択肢の中から選べ。
(1)環境
(2)パーソナリティ
(3)報酬
(4)エージェント
解答:2
4.
次の中から価値ベースの手法を次の選択肢の中から選べ。
(1)Q学習
(2)A3C
(3)PGPE
(4)REINFORCE
解答:1
5.
Experience Replayについて誤った記述を次の選択肢の中から選べ。
(1)off policyにもon policyにも使える
(2)RNNには使えない
(3)状態S、行動a、行動価値Qをすべて保存してランダムサンプリングするためメモリを使う
(4)データに強い相関があるときでも使用できる
解答:1
深層学習の適応方法
画像認識
1.
(a)(b)(c)に当てはまる語句を選べ。
AlexNetはIVSVRC2012で優勝した画像認識モデルであり、畳み込みネットワークの先駆けとなったモデルである。AlexNetを改良したモデルが(a)であり、畳み込み13層とFC層を3層持つのが特徴である。(a)の概要は、
1.カーネルサイズ(b)の畳み込みを何度か繰り返す
2.(c)を行う
3.2.の後チャンネル数を倍にするという流れである。
(a):
(1)GoogleNet
(2)VGG16
(3)ResNet
(4)DenseNet
解答:2
(b):
(1)1
(2)3
(3)5
(4)16
解答:2
(c):
(1)Average Pooling
(2)Max Pooling
(3)Grobal Average Pooling
(4)カーネルサイズ5*5の畳み込み
解答:2.
2.
GoogleNetに用いられていないものを次の選択肢の中から選べ。
(1)Point wise 畳み込み
(2)Inception module
(3)カーネルサイズ1*1の畳み込み
(4)Auxiliary Loss
解答:1
3.
(a)(b)に当てはまる語句を選べ。kをカーネルサイズ、nを画像のch数とする。
MobileNetとはXceptionなどに用いられた畳み込みの手法を用いて計算量を大幅に削減した手法である。
Xceptionと異なるのはResNetのようなショートカットを用いない点、(a)のdepthwise畳み込みと(b)のpointwise畳み込みの間に(c)と(d)を利用している点が挙げられる。
(a)(b)
(1) (a)kk1 (b)11n
(2) (a)k11 (b)1kn
(3) (a)11n (b)kk1
(4) (a)1kn (b)k11
解答:1
(c)
(1)Layer normalization
(2)Instance normalization
(3)Batch normalization
解答:3
(d)
(1)Leaky RelU
(2)RelU
(3)Sigmoid
(4)Tanh
解答:2
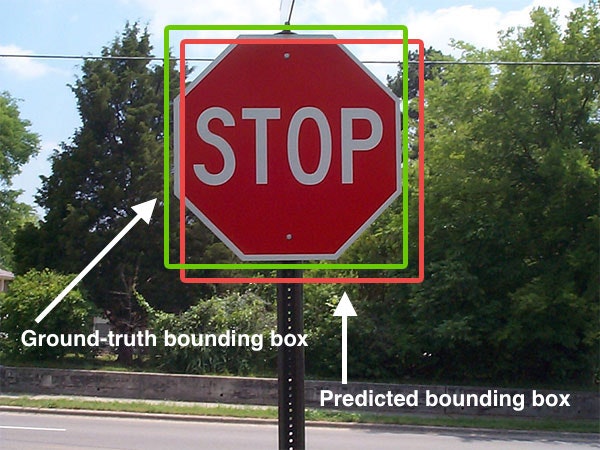
4.
下の図において赤枠が予測されたbounding boxで緑枠が正しいbounding boxである。
緑枠、赤枠の大きさが2500、重なった部分が2000、緑枠∨赤枠が4000の時IOUの値を選べ。
画像引用:http://kenbo.hatenablog.com/entry/2018/04/27/124749
(1)0.4
(2)0.5
(3)2
(4)2.5
解答:2
5.
R-CNNの記述について誤った選択肢を次の選択肢の中から選べ。
(1)物体の位置検出には回帰を利用して正確な位置が出力できるようにしている。
(2)処理時間を高速化するために、予め物体がありそうな場所を検出しておき、その候補領域についてのみCNNによる物体認識を行う。
(3)物体の位置検出から認識までをend-to-endで行う。
(4)画像の縦横比を無視して決まった形にリサイズする。
解答:3
6.
次の選択肢からあやっているものを選べ。
(1)Faster R-CNN ではselective searchを使わず、物体の候補領域の抽出もネットワークに組み込む手法である。
(2)Fast R-CNNでは認識とbounding boxの計算を同時に行う。
(3)smooth L1 Lossは画像のクラス分類の評価に用いられる。
(4)抽出と認識を一度の処理で行う手法とone-shotと呼ばれる。
解答:3
7.
YOLOについて正しい記述を次の選択肢の中から選べ。
(1)Faster R-CNNより精度が良い。
(2)狭い場所に大量に物体があると検知ができなくなる。
(3)候補領域の抽出が終わったのち認識を行う。
(4)20クラス分類、分割数7、1グリッド当たりのbounding boxの数が2であれば、7740のテンソルが出力される。
解答:2
8.
SSDについて正しい記述を次の選択肢の中から選べ
(1)デフォルトボックスを仮置きし、bounding boxを大きくしてマッチさせる
(2)仮置きされるデフォルトボックスの数は500個程度である
(3)GoogLeNetをベースにしたCNNが用いられる
(4)Hard negative miningではすべて背景領域と判定しないように負例と正例の比が最大で5:1になるよう調整する
解答:1
自然言語処理
1.
(a)(b)(c)に当てはまる語を次の選択肢の中から選べ
単語をベクトルにするには様々な手法があり、例えばone hot encordingが挙げられる。しかしこの手法ではメモリの効率が悪く、ベクトルの類似度が単語の類似度として使えない。そこでword2vecでは類似した文脈に出る単語は似た意味を持つという(a)をもとに設計された手法であり、ベクトルの類似度が単語の類似度として使えるほか、メモリを効率よく使えるメリットがある。(b)と(c)があり、(b)では周辺単語を入力として単語を予測する事前学習からベクトルを得る手法であり(c)より学習が高速である。(c)は与えられた単語から周辺単語を予測する事前学習からベクトルを得る手法であり、(b)より精度が少し高い。
(a)
(1)分散仮説
(2)分布仮説
(3)万能近似定理
(4)近似仮説
解答:2
(b)(c)
(1)(b):CBOW (c)skip-gram
(2)(b):juman++ (c)skip-gram
(3)(b):skip-gram (c):CBOW
(4)(b):CBOW (c)sentence piece
解答:1
2.
次の選択肢からAttentionについて正しい記述を次の選択肢の中から選べ。
(1)RNNと同様に逐次処理である
(2)Transformerのデコーダーの出力を特徴ベクトルとして扱う
(3)他の手法と比べてデータ同士の関連を調べるのに必要な処理数が多い
(4)self attentionにより特徴抽出を行う
解答:4
3.
次の選択肢からAttentionのEncorderに用いられていない構造を次の選択肢の中から選べ。
(1)skip connection
(2)positional encording
(3)soft max
(4)Layer Normalization
解答:3
4.
Masked Language Modelの入力で用いられないものを次の選択肢の中から選べ。
(1)Token Embedding
(2)position Embedding
(3)Segment Embedding
(4)上記にはない
解答:4
5.
(a)に当てはまる選択肢を次の選択肢の中から選べ
Masked Language Modelではランダムに(a)%のtokenを選び、選ばれたtokenのうち80%をmaskに置き換え穴埋め問題を解かせ、10%をランダムなtokenに置き換え、残りの10%には何もしない。
(1)5
(2)10
(3)15
(4)30
解答:3
Text to Speach
1.
wavenetのベースになった手法を次の選択肢の中から選べ。
(1)PixelCNN
(2)Text to Speach
(3)pix2pix
(4)talk navi
解答:1
2.
wavenetについて誤った特徴を次の選択肢の中から選べ。
(1)活性化関数にはRelUが用いられる。
(2)dilated causal convolutionを用いることで受容体を広げた。
(3)計算負荷を減らすために音声を256クラスのカテゴリ変数に変換し、生成する音声がどのクラスに属するかという分類問題を解いている。
(4)残差ブロックとスキップコネクションをネットワーク全体に採用することで、「より深い学習」と「多様な特徴抽出」を可能にしている。
解答:1 GTUが用いられる
その他
1.
$r$:人間が翻訳した文の長さ
$c$:機械が翻訳した文の長さ
$w_n$:重み
$p_n$:modified n-gram precisions
としたときのBLEUスコアの定義式を次の選択肢の中から選べ。
(1)$(1-\frac{r}{c}) exp(\sum_{n=1}^{N}p_{n}logw_{n})$
(2)$e^{(1-\frac{r}{c})} exp(\sum_{n=1}^{N}w_{n}logp_{n})$
(3)$(1-\frac{r}{c}) exp(\sum_{n=1}^{N}p_{n}logw_{n})$
(4)$e^{(1-\frac{r}{c})} exp(\sum_{n=1}^{N}w_{n}logp_{n})$
解答:4
2.
BLEUスコアの説明として誤っているものを次の選択肢の中から選べ。
(1)modified n-gram precisionにより同じ単語は繰り返せないという制約を付けている。
(2)人間の翻訳文より機械の翻訳文が長いとペナルティがつく。
(3)人間が翻訳した文章に似ていれば似ているほど、機械が翻訳した文は正しそうだという前提に基づいている。
(4)翻訳タスク以外にも流用される。
解答:4
軽量化・高速化技術
1.
次の選択肢から誤っているものを次の選択肢の中から選べ。
(1)枝刈りとは重みが0のノードを消す手法である。
(2)蒸留とはあるモデルAの出力を教師データとして別のモデルに学習させる手法であり、Adversarial Exampleに強くなる。
(3)Adversarial Exampleの対策としてアンサンブル学習が挙げられる。
(4)量子化によりモデルのサイズを小さくでき、特に1bitの量子化をbinarizationと呼ぶ。
解答:3
ここまでです、最後まで解いていただきありがとうございました。
不備等があれば指摘してくださると幸いです。
参考文献
https://gangango.com/2019/06/16/post-573/
https://qiita.com/arajiru/items/d675000a0d4dac37d8be
https://teratail.com/questions/205514
https://ai-scholar.tech/articles/treatise/waven-ai
ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装
ゼロから作るDeep Learning ❷ ―自然言語処理編
https://qiita.com/arajiru/items/d675000a0d4dac37d8be