来年のE資格に向けて予想問題集を作りました。
今回は機械学習編、分かっているのは
・出題範囲
・回答は選択式
の2つです。何か不備があるかもしれませんが復習がてらお使いください。
解答は白文字で記入しているので、文字を選択すれば見れます。
不備等があれば指摘してくださると幸いです。
深層学習はこちら
https://qiita.com/MeiByeleth/items/c9256c029852ab3a9487
数学はこちら
https://qiita.com/MeiByeleth/items/e71c631185cd5d39a705
機械学習の基礎
データセットについて
1.
次の空欄(ア)~(ウ)に入る語を(1)~(7)から選べ。
機械学習を行うにあたってデータには3種類あり、(ア)、(イ)、(ウ)がある。それぞれのデータは
(ア)はパラメータの学習、
(イ)はモデル選択、
(ウ)は性能の測定
に用いられる。
(1)訓練データ
(2)情報
(3)エントロピー
(4)テストデータ
(5)ハイパーパラメータ
(6)バッチ
(7)検証データ
解答
(ア):1
(イ):7
(ウ):4
過学習
1.
過学習をしやすい条件として誤っているものを次の選択肢の中から選べ。
(1)モデルの自由度が低い
(2)特徴量が多い
(3)学習データの数が少ない
(4)学習データにノイズ、外れ値が多い
解答:1
2.
次のうちRidge回帰の損失関数Eの式を次の選択肢の中から選べ。ただし、$E_0$はコスト関数、$\lambda$は正則化パラメータとする。
(1)$E=\lambda E_0+\lambda \sum_{k=1}^{n} |w_k|^2 $
(2)$E=\lambda E_0+\lambda \sum_{k=1}^{n} |w_k| $
(3)$E=E_0+\lambda \sum_{k=1}^{n} |w_k|^2 $
(4)$E=E_0+\lambda \sum_{k=1}^{n} |w_k| $
解答:3
3.
次のうちLasso回帰について誤った記述を次の選択肢の中から選べ。ただし、$E_0$はコスト関数、$\lambda$は正則化パラメータとする。
(1)損失関数Eは$E_0+\lambda \sum_{k=1}^{n} |w_k| $と表せる。
(2)計算量、メモリ削減の効果が期待される。
(3)Dropoutの手法の一つである。
(4)正則化により過学習低減が期待される。
解答:3
ハイパーパラメータ
1.
次のうちハイパーパラメータではない選択肢を次の中から選べ。
(1)ニューロンの重み$w$
(2)学習率
(3)LEAKY ReLUの$\alpha$
(4)ランダムフォレストの木の深さ
解答:1
検証集合
1.
交差検証の説明として誤っている選択肢を次の中から選べ。
(1)学習データを訓練セットとテストセットに分けて行う手法である。
(2)すべてのデータが一度検証に使われ、検証に重複がない。
(3)ホールドアウト法を複数回繰り返すのでより信頼度があがる。
(4)複数回の検証の中で一番良いスコアを交差検証のスコアとして使用する。
解答:4
最尤推定
1.
n個の観測値 x1, x2, ..., xn があるとする。n個のデータが同じ正規分布 N(μ, σ) に従うとするとき、μの値を最尤法より推定しμの値を次の選択肢の中から選べ。
(1)μ=0
(2)μ=σ
(3)μ=$ \frac{1}{n}\sum_{i=1}^{n}x^2_{i}$
(4)μ=$ \frac{1}{n}\sum_{i=1}^{n}x_{i}$
解答:4
教師ありアルゴリズム
1.
k-近傍法を実装するためのknn関数を実装したい。
(a)に入るコードを選べ。
def knn(k, train_data, test_data):
labels = []
for test in test_data:
distances = (a)
sorted_train_indexes = np.argsort(distances)
sorted_k_labels = train_data[sorted_train_indexes, -1][:k]
label = Counter(sorted_k_labels).most_common(1)[0][0]
labels.append(label)
return labels
(1)np.sum((train_data[:,:-1]-test[:-1]) ** 2, axis=1)
(2)np.sum((train_data[:,:-1]-test[:-1]) ** 2, axis=1)
(3)np.sum((train_data[:,:-1] ** 2-test[:-1] ** 2), axis=1)
(4)np.sqrt((train_data[:,:-1]** 2-test[:-1]** 2), axis=1))
解答:1
2.
次の選択肢の中から正しいものを選べ。
(1)
(2)np.sum((train_data[:,:-1]-test[:-1]) ** 2, axis=1)
(3)np.sum((train_data[:,:-1] ** 2-test[:-1] ** 2), axis=1)
(4)np.sqrt((train_data[:,:-1]** 2-test[:-1]** 2), axis=1))
解答:1
教師なしアルゴリズム
1.
主成分分析を行うPCAクラスを実装したい。(a),(b)に入るコードを選べ。
class PCA:
def __init__(self, n_components=2):
self.n_components = n_components
def fit_transform(self, X):
(a)
# 固有値と固有ベクトルを求めて固有値の大きい順にソート
l, v = np.linalg.eig(self.cov_)
l_index = np.argsort(l)[::-1]
self.l_ = l[l_index]
self.v_ = v[:,l_index]
self.components_ = self.v_[:,:self.n_components].T
T = (np.mat(X)*(np.mat(self.components_.T))).A
# 出力
return T
(1)
X = (x - x.mean())/x.std(ddof=0)
self.cov_ = np.cov(X, rowvar=False)
(2)
X = (x - x.mean())
self.cov_ = np.cov(X, rowvar=False)
(3)
self.cov_ = np.cov(x, rowvar=False)
(4)
X = x/x.std(ddof=0)
self.cov_ = np.cov(X, rowvar=False)
解答:1
2.
カーネル法の計算量は何に依存するか。次の選択肢の中から選べ。
(1)特徴量
(2)カーネル法の次元数
(3)データセットのデータ数
(4)写像後の次元数
解答:3
確率的勾配降下法
1.
確率的勾配降下法の数式を次の選択肢の中から選べ。ただしLは損失関数、Wは重み、$\eta$は学習率とする。
(1)$W←W-\eta W$
(2)$W←W-\eta\frac{\partial L}{\partial W}$
(3)$W←W+\eta\frac{\partial L}{\partial W}$
(4)$W←W+\eta W$
解答:2
深層学習の発展を促す課題
1.
正しい記述を次の選択肢の中から選べ。
(1)特徴量が多すぎると逆に過学習してしまうことを次元の呪いという。
(2)勾配ブースティングはランダムフォレストを並列に並べ多数決をとるモデルである。
(3)分類モデルの評価にはAccuracyを用いればよい。
(4)サポートベクトルマシーンはカーネルトリックによりかえって計算の次元が増えてしまうのでより計算コストが高くなる。
解答:1
実用的な方法論
性能指標
1.
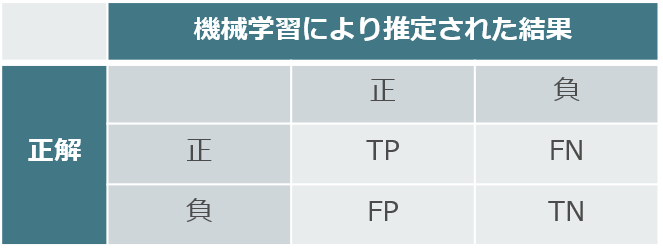
ある機械学習のモデルが分類タスクを行った結果を以下に示す。
引用:https://tips-memo.com/python-f-measure
この時、適合率(=PRE)、F値の式を選べ。再現率をRECとする。
(1)$PRE=\frac{TP}{TP+FP},F=\frac{TP+TN}{TP+FP+FN+TN}$
(2)$PRE=\frac{TP}{TP+FN},F=\frac{TP+TN}{TP+FP+FN+TN}$
(3)$PRE=\frac{TP}{TP+FP},F=\frac{2\mathrm{REC}\cdot\mathrm{PRE}}{\mathrm{REC}+\mathrm{PRE}}$
(4)$PRE=\frac{TP}{TP+FN},F=\frac{2\mathrm{REC}\cdot\mathrm{PRE}}{\mathrm{REC}+\mathrm{PRE}}$
解答:3
ハイパーパラメータの選択
1.
ハイパーパラメータチューニングの手法を次の選択肢の中から選べ。
(1)グリッドサーチ
(2)ホールドアウト
(3)svm
(4)主成分分析
解答:1
参考文献
https://stats.biopapyrus.jp/probability/gaussian.html
https://www.haya-programming.com/entry/2018/03/28/222101
https://www.sejuku.net/blog/64355
http://enakai00.hatenablog.com/entry/2017/10/13/145337
https://qiita.com/arajiru/items/d675000a0d4dac37d8be
Pythonではじめる機械学習――scikit-learnで学ぶ特徴量エンジニアリングと機械学習の基礎