今回は時系列データの処理に使うNNの比較をしました。
手法の解説
RNN(回帰結合型ニューラルネットワーク)とは
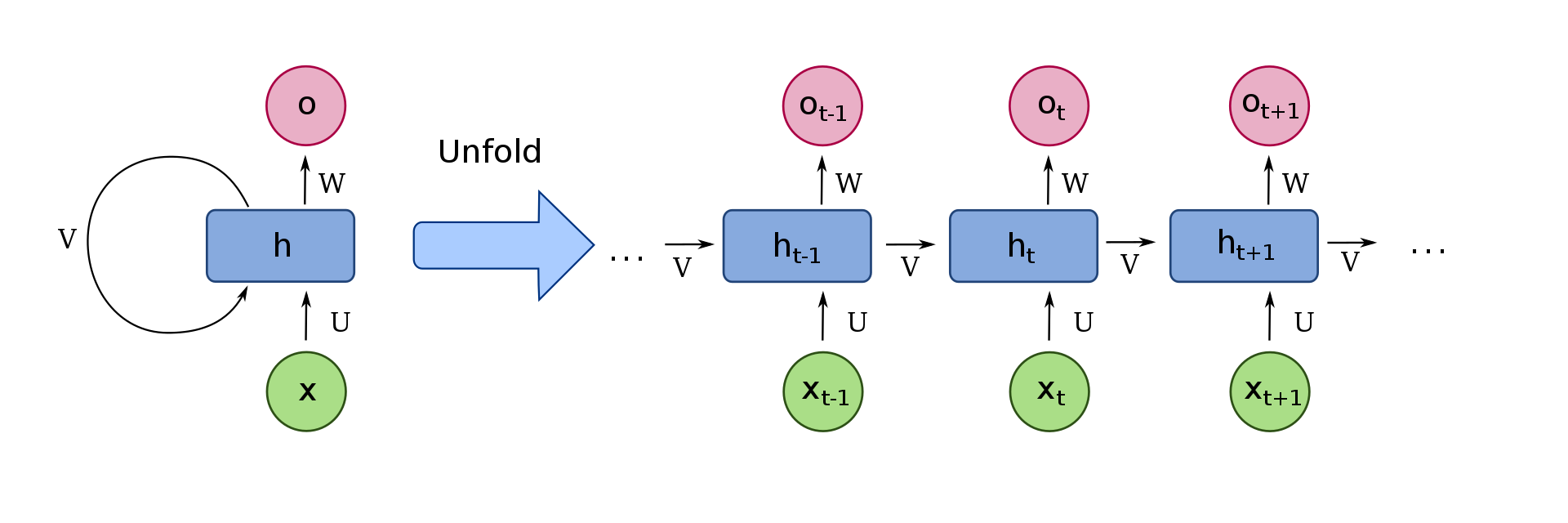
RNN(回帰結合型ニューラルネットワーク)とは、出力が入力に戻るループ構造のネットワークです。
英語ではRecurrent neural networkといいます。
下図でいう左側に当たります。この構造を展開すると右側のようになり、誤差逆伝播法が可能です。RNNでの誤差逆伝播法
はBPTT(通時的誤差逆伝播法)と呼びます。
LSTM
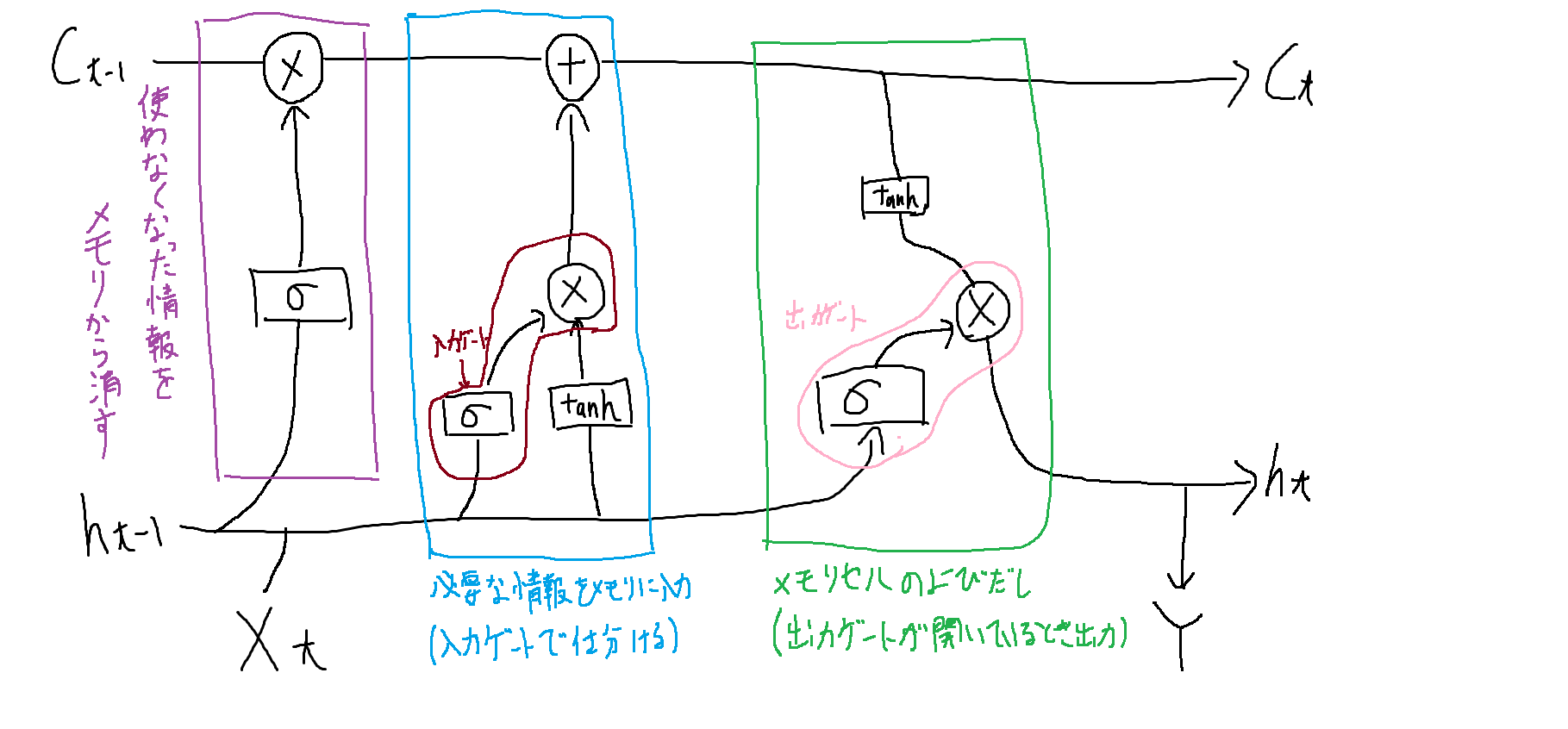
RNNでネットワークが大きくなってしまい、過去の情報を保持できない(=勾配が消失する)問題が出てしまいます。
そこで忘却ゲート、入出力ゲート、メモリを搭載し、解決した手法。
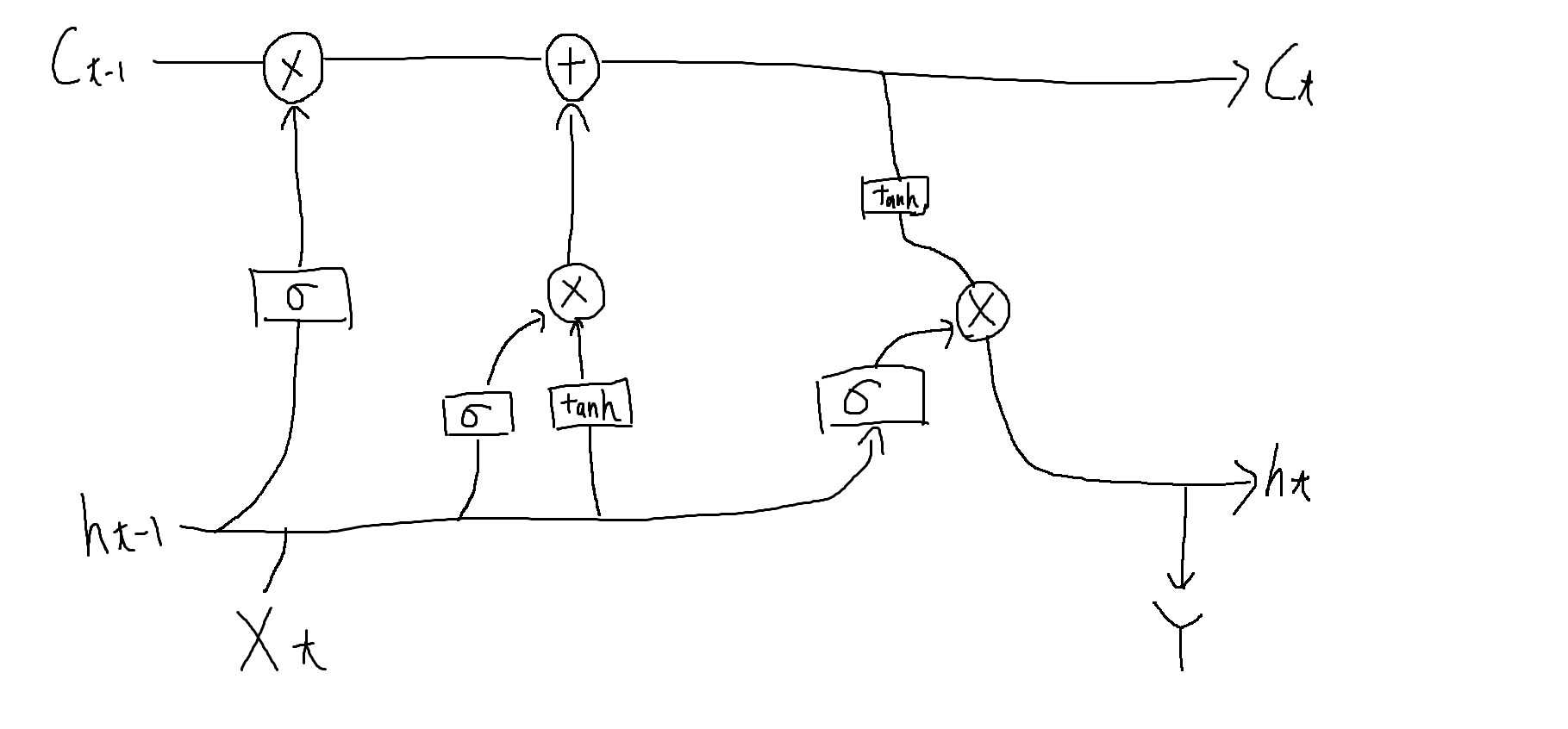
それぞれ以下の役割を持っています。
ゲートを設けたため、勾配が消失する問題を解決しました。
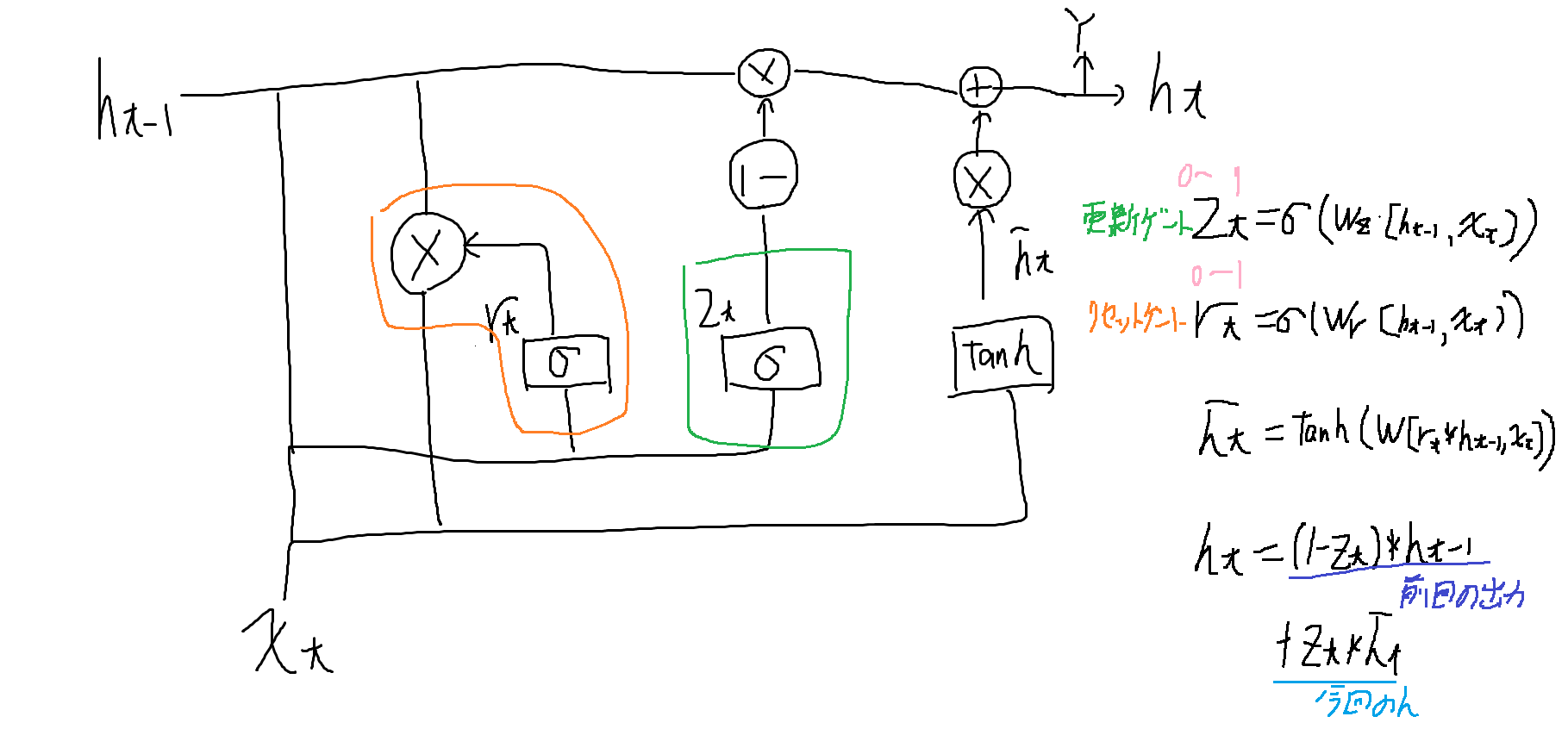
GRU
メモリセルをなくして忘却ゲートと入力ゲートを合体させたモデル。
ゲートが更新ゲートとリセットゲートの二種類になります。
手法の比較
ではRNN、LSTM、GRUで戦わせます。
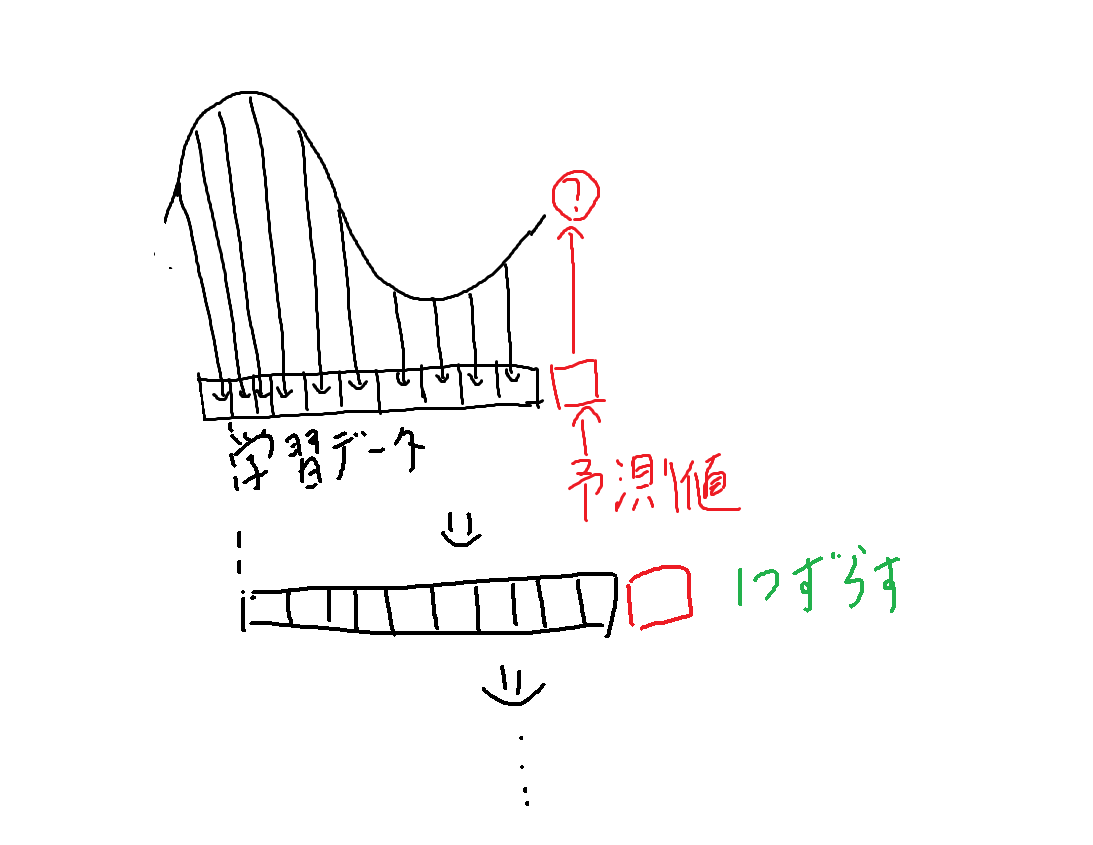
今回解いた問題はノイズを混ぜたコサイン波を学習データとし、次の値を予測させる問題です。
ノイズを与えた10個の値を学習データ、11個目のデータを正解の値とし、1個ずらしてまた10個のデータを作りを繰り返します。
10個のデータ*40セットを学習データのセットとします。
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
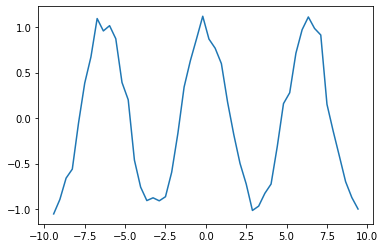
x_data = np.linspace(-3*np.pi, 3*np.pi)
cos_data = np.cos(x_data) + 0.1*np.random.randn(len(x_data))
plt.plot(x_data, cos_data)
plt.show()
n_rnn = 10 # 時系列の数
n_sample = len(x_data)-n_rnn #サンプル数
x = np.zeros(n_sample, n_rnn) #入力
t = np.zeros(n_sample)
for i in range(0, n_sample):
x[i] = cos_data[i:i+n_rnn]
t[i] = cos_data[i+n_rnn]#正解データは最後の時刻のみ
x = x.reshape(n_sample, n_rnn, 1) #サンプル数、時系列の数、入力層のニューロン数
print(x.shape)
t = t.reshape(n_sample, 1) #サンプル数、入力層のニューロン数
print(t.shape)
モデルの比較
それではNNを構成していきます。kerasにすでにLSTMとRNN、GRUがすでに実装されているのでそちらを使います。
from keras.models import Sequential
from keras.layers import Dense, LSTM, GRU, SimpleRNN
batch_size = 8 # バッチサイズ
n_in = 1 #入力層のニューロン数
n_mid = 20 #中間層のニューロン数
n_out = 1 #出力層のニューロン数
# 誤差は二乗誤差、最適化アルゴリズムはSGD
# RNN
model_rnn = Sequential()
model_rnn.add(SimpleRNN(n_mid, input_shape=(n_rnn, n_in), return_sequences=False))# return_sequenceをTrueをFalseにすると、最後のRNN層のみが出力を返す。
model_rnn.add(Dense(n_out, activation="linear"))
model_rnn.compile(loss="mean_squared_error", optimizer="sgd")
print(model_rnn.summary())
# LSTM
model_lstm = Sequential()
model_lstm.add(LSTM(n_mid, input_shape=(n_rnn, n_in), return_sequences=False))
model_lstm.add(Dense(n_out, activation="linear"))
model_lstm.compile(loss="mean_squared_error", optimizer="sgd")
print(model_lstm.summary())
# GRU
model_gru = Sequential()
model_gru.add(GRU(n_mid, input_shape=(n_rnn, n_in), return_sequences=False))
model_gru.add(Dense(n_out, activation="linear"))
model_gru.compile(loss="mean_squared_error", optimizer="sgd")
print(model_gru.summary())
結果
Model: "sequential_30"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
simple_rnn_10 (SimpleRNN) (None, 20) 440
_________________________________________________________________
dense_28 (Dense) (None, 1) 21
=================================================================
Total params: 461
Trainable params: 461
Non-trainable params: 0
_________________________________________________________________
None
Model: "sequential_31"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
lstm_10 (LSTM) (None, 20) 1760
_________________________________________________________________
dense_29 (Dense) (None, 1) 21
=================================================================
Total params: 1,781
Trainable params: 1,781
Non-trainable params: 0
_________________________________________________________________
None
Model: "sequential_32"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
gru_10 (GRU) (None, 20) 1320
_________________________________________________________________
dense_30 (Dense) (None, 1) 21
=================================================================
Total params: 1,341
Trainable params: 1,341
Non-trainable params: 0
_________________________________________________________________
None
パラメータ数はLSTM、GRU、RNNの順に多いです。
時間の比較
学習にどれくらい時間がかかるのか見ていきましょう。
import time
epochs = 300
# RNN
start_time = time.time()
history_rnn = model_rnn.fit(x, t, epochs=epochs, batch_size=batch_size, verbose=0)
print("RNN:", time.time() - start_time,'[s]')
# LSTM
start_time = time.time()
history_lstm = model_lstm.fit(x, t, epochs=epochs, batch_size=batch_size, verbose=0)
print("LSTM:", time.time() - start_time,'[s]')
# GRU
start_time = time.time()
history_gru = model_gru.fit(x, t, epochs=epochs, batch_size=batch_size, verbose=0)
print("GRU:", time.time() - start_time,'[s]')
実行結果
RNN: 9.410311222076416 [s]
LSTM: 24.702671766281128 [s]
GRU: 31.10002875328064 [s]
RNN、LSTM、GRU順になりました。
パラメータ数順になると思っていたのですがそうではないみたいです。
予測結果
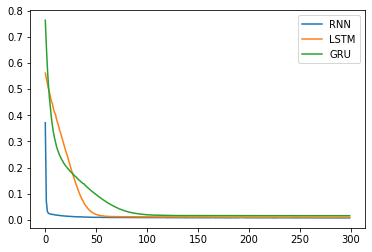
訓練誤差の推移を見ましょう。
loss_rnn = history_rnn.history['loss']
loss_lstm = history_lstm.history['loss']
loss_gru = history_gru.history['loss']
plt.plot(np.arange(len(loss_lstm)), loss_rnn, label="RNN")
plt.plot(np.arange(len(loss_lstm)), loss_lstm, label="LSTM")
plt.plot(np.arange(len(loss_gru)), loss_gru, label="GRU")
plt.legend()
plt.show()
RNN早すぎる・・・。GRUは緩やかでLSTMは急に収束。
ネットワークの大きさが小さいのでパラメータが少ないRNNが良い結果になったと推測できます。
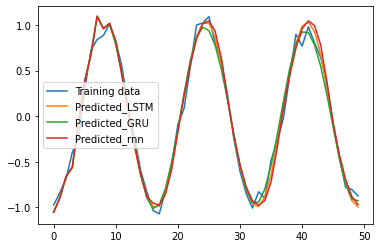
ちなみに予測結果をプロットするとこう。
predicted_rnn = x[0].reshape(-1)
predicted_lstm = x[0].reshape(-1)
predicted_gru = x[0].reshape(-1)
for i in range(0, n_sample):
y_rnn = model_rnn.predict(predicted_rnn[-n_rnn:].reshape(1, n_rnn, 1))
predicted_rnn = np.append(predicted_rnn, y_rnn[0][0])
y_lstm = model_lstm.predict(predicted_lstm[-n_rnn:].reshape(1, n_rnn, 1))
predicted_lstm = np.append(predicted_lstm, y_lstm[0][0])
y_gru = model_gru.predict(predicted_gru[-n_rnn:].reshape(1, n_rnn, 1))
predicted_gru = np.append(predicted_gru, y_gru[0][0])
plt.plot(np.arange(len(cos_data)), cos_data, label="Training data")
plt.plot(np.arange(len(predicted_lstm)), predicted_lstm, label="Predicted_LSTM")
plt.plot(np.arange(len(predicted_gru)), predicted_gru, label="Predicted_GRU")
plt.plot(np.arange(len(predicted_rnn)), predicted_rnn, label="Predicted_rnn")
plt.legend()
plt.show()
結果
どの手法もきれいに予測できました。もっと大きいデータでやっても予測ができるのか調査していきたいです。
まとめ
・RNN、LSTM、GRUの手法の比較をノイズを混ぜたコサイン波の次の値を予測させて行った。
・どの手法も同等に予測ができたが、RNN、LSTM、GRUの順に精度がよく、RNNが最も訓練誤差の収束が早かった。
・今後は長い時系列データを用いた比較を行いたい。
以上になります。