順伝播型ネットワークの項目と学習について書きます。
目次
DeepLearningの歴史
まずディープラーニングがどのように発展していったのかお話しします。
第一次ニューラルネットワークブーム
ある時、脳の神経細胞を仕組みを再現した人工ニューロンを作ります。
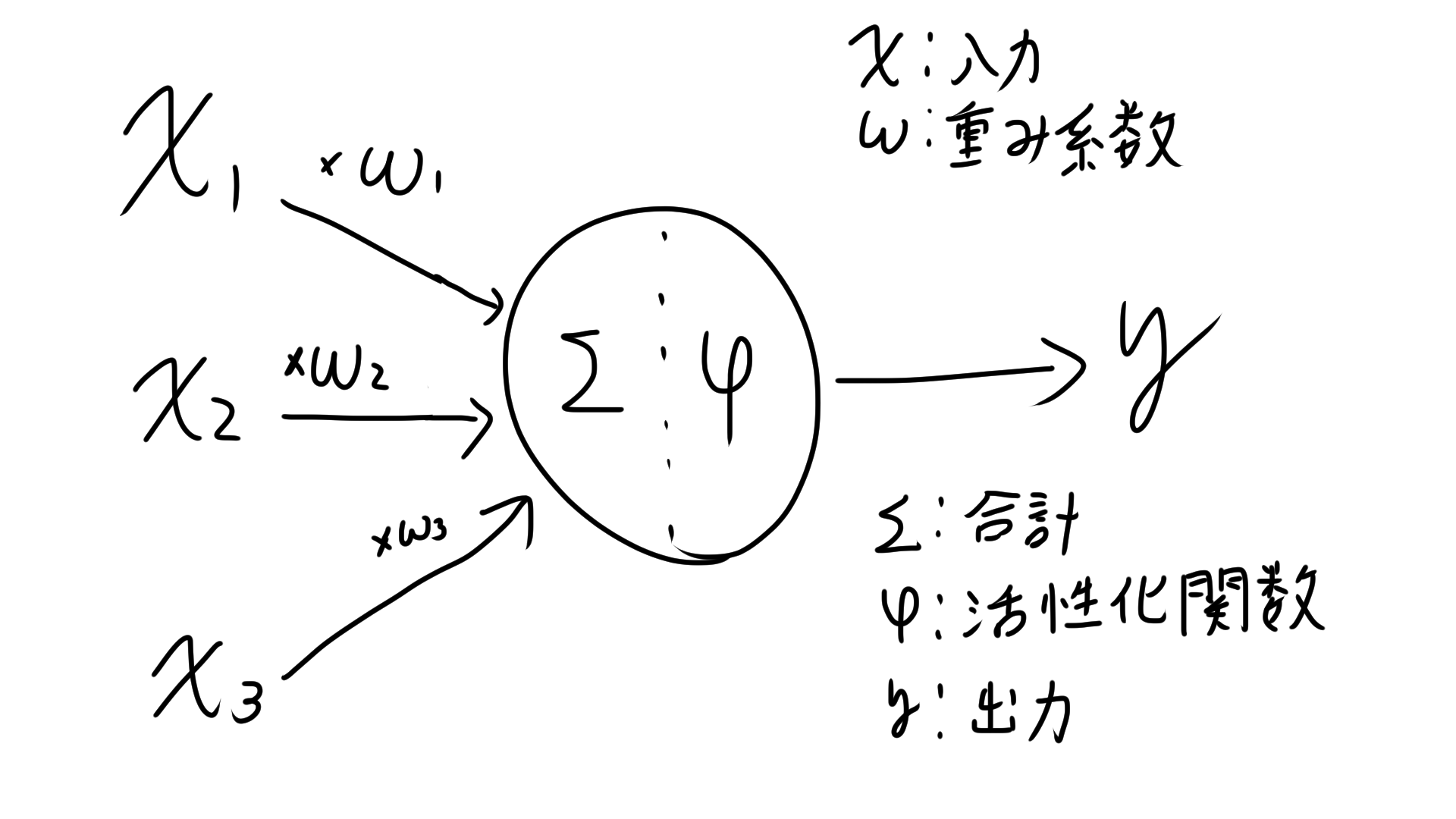
人工ニューロンとは上図のようなものを指します。
この複数の信号から1つの信号を出力するアルゴリズムをパーセプトロンと呼びます。
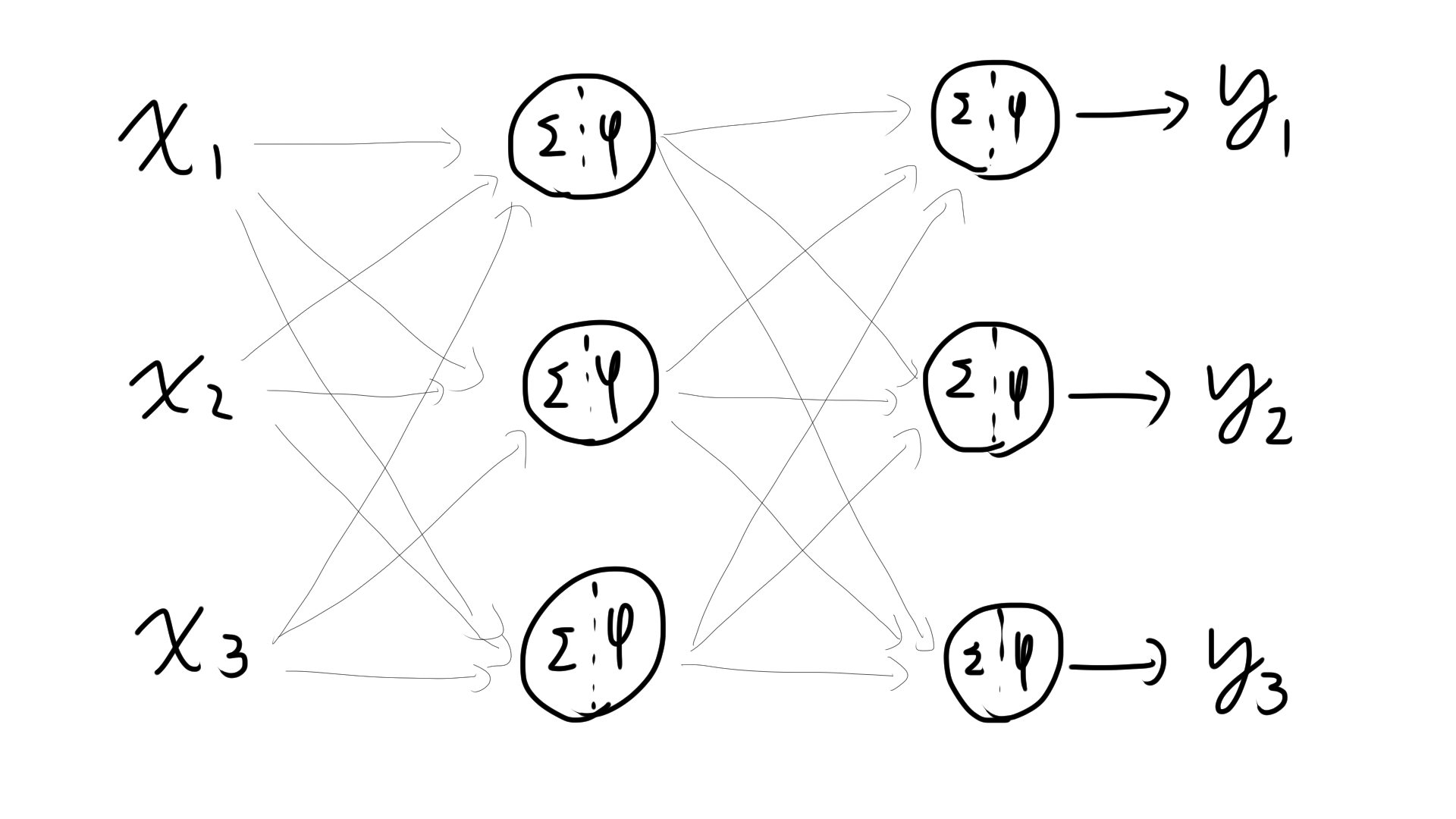
この人工ニューロンを2つ重ねるとが学習できるらしくブームが起こります。下図。
ですが世の中の多くを占めている非線形の問題が解けなく、ブームが終わります。
第二次ニューラルネットワークブーム
実は3層以上重ねるとどうやら非線形問題が解けることは知られていましたが、誰も実装まで手が付けられませんでした。
ところがある時、BackPropagationという方法が発見され、3層以上を重ねられました。
何層も重ねたものをニューラルネットワークと呼びます。
(アルゴリズムを多層パーセプトロンといいます。)
ニューラルネットワークのうち、一方通行でループがないものをFeed-forward NN、4層以上を後述するDeepLearning(DNN)と呼びます。
んでひたすら層を増やしまくったら性能が上がるのでは・・・と皆さん考え研究をしますが、逆に性能は落ちてしまいました。結局ブームが終わります。
このような入力から出力まで一方向に演算が進むネットワークを順伝播型ネットワークといいます。
DeepLearning登場
2010年、DeepLearningというアルゴリズムが画像認識コンテストで圧勝します。
以前まで層を重ねていても性能が上がらなかったのですがこのDeepLearningは4層以上重ねて性能を向上させ、一躍有名に。再びニューラルネットワークにブームが訪れます。
分析の流れ
ここではDeepLearningがどんな手法で解いているかお話しします。
機械学習が考案される前の場合
データx
↓
人間が考えた手法A
↓
人間が考えた手法B
↓
人間が考えた手法C
↓
結果:y
すべて人間がデータの前処理から計算まで手で行っていました。
機械学習の場合
機械学習が考案され、どうデータを入れれば機械学習を適切にできるかにフォーカスが向きます。
データx
↓
人間が考えた手法A
↓
人間が考えた手法B
↓
機械学習(SVM,リッジ回帰など)
↓
結果:y
DeepLearningの場合
DeepLearningではデータを渡すだけ、正直内部で何やっているか不明な点も多いです。
データx
↓
Deep Learning(なにやっているかよくわからないけどなぜかうまくいく)
↓
結果:y
何やっているかよくわからないものを使うなよと言われるのも無理もないのですが、人間が考えた汎用的な方法より、DeepLearningが最適化した処理のほうが優れているので急激に広まりました。
学習方法
教師ありのモデルの学習は、この図でいうWを最適化、つまり正解データの値yと予測値の差φ(wx)をいかに小さくするかです。
この差を見るために損失関数を用います。
損失関数
学習では何かの基準で悪さを決め、その悪さが少なくなるようパラメータ(重みW)を学習(更新)させます。その基準を損失関数(コスト関数)$E$といいます。
いかに一部の例を紹介します。
cross entropy
$$
E=-ylog(t)-(1-y)log(1-t)
$$
$t$は予測値、$y$は正解の値を示します。
使われ方の例ですと、天気予測モデルA,Bがあり
モデルA:99%の確率で晴れ、よって明日は晴れ
モデルB:50%の確率で晴れ、よって明日は晴れ
と予測し、正解は雨だったとします。
このとき、どのくらい間違えているかの指標になります。つまりAはたくさんまちがえていて、B は惜しい予測をしたと判断できます。
つまりどれくらい間違えているかの指標といえるでしょう。
メリットとしては
・間違っていたら$E$をかなり大きく、正解に近いととても小さくなる
・計算が簡単
・情報工学で使われる関数と相性がいい
があげられます。
最尤推定
入力xがあったとき、正解yが出る事後確率を$p(y_t|x,w)$とします。この時、P最大にするx,wの組み合わせを求めるのが最尤推定です。
xは不変なのでwを変えます。
ちなみに式は
$$
p(c=t|x)=y^t (1-y)^{(1-t)}
$$
です。y:出力結果(0~1)、tは正解ラベル(0,1)を指します。
これは一つのニューロンでの結果なのでこれらをネットワークにあるすべてのニューロンで適用すると
$$
logL(w)=l=\sum_{p=1}^{P}\sum_{k=1}^{k} (t_{pk}logz_{pk}+(1-t_{pk})log(1-z_{pk})) \
$$
計算過程は省略します。
対数をとって計算しやすくしています。なぜか不思議なことにクロスエントロピーと似た式が出てきます。
値の更新方法
次にwの更新方法について。
勾配降下法
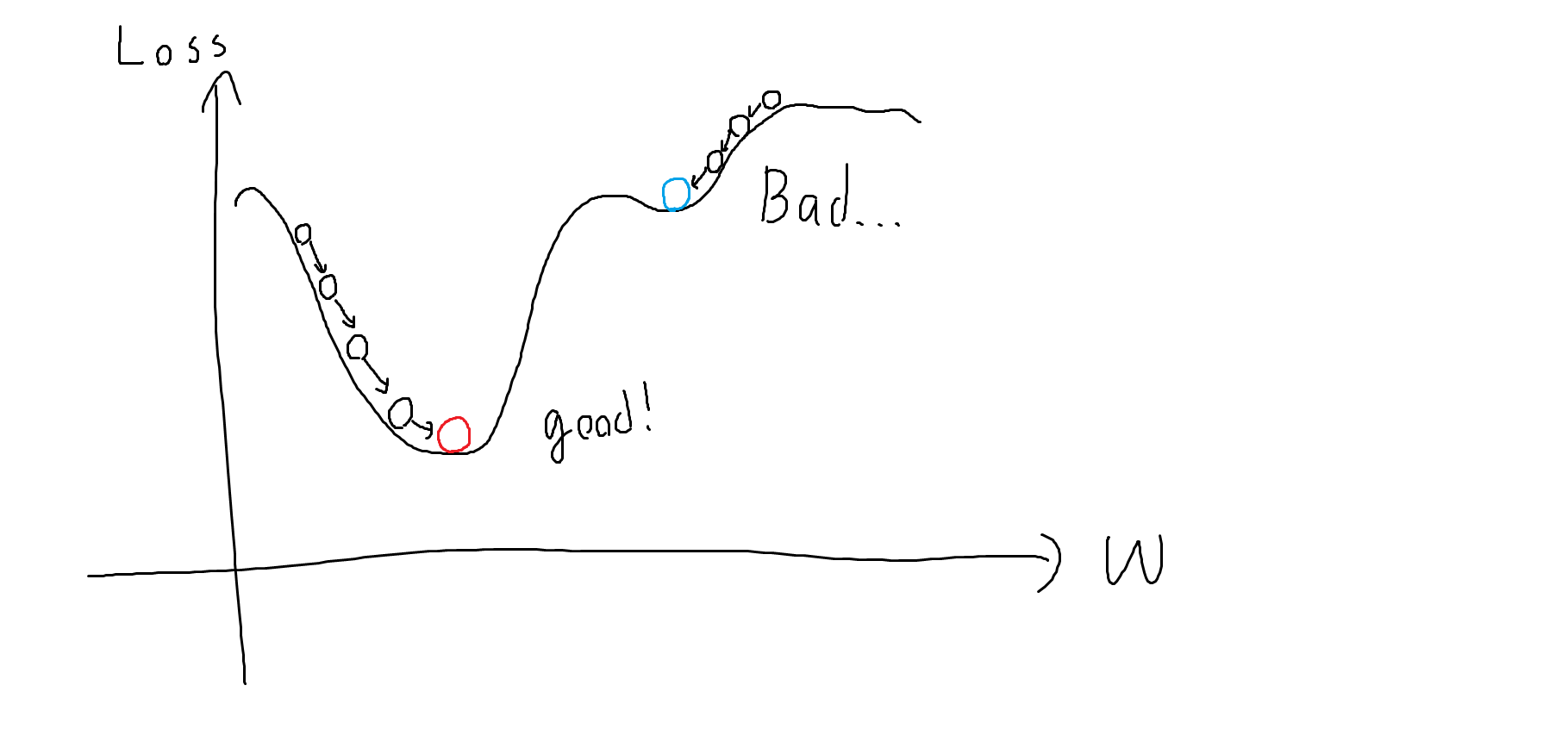
絵のようにwを最小となる場所に勾配を見ながら下げていく方法です。
ただこれらは
・局所最適解に陥いる可能性
・山を乗り越えてしまう可能性(崖と勾配爆発、勾配クリッピングというwの更新幅を制限することで対応)
・wは大量(10万から1億)ぐらいあり、一個ずつ求めていると途方もない時間がかかる。
と欠点を抱えています。これらの問題を解決したのがSGDです。
確率的勾配降下法(SGD)
学習データを一部ずつとり、BackPropagationで計算する手法。
学習データを一部ずつとるのでグラフの形が変わります、結果局所最適解に陥らずに山を越えやすくなります。
バッチ、ミニバッチ、オンライン学習
バッチとは学習データを全て学習に突っ込むやり方です。すべてのデータを保持しながらやるので計算コストが高く、GPUで計算しきれないです。
オンライン学習は1データ毎に重みを更新するやり方、学習が安定しないのであまり使われません。
2つのいいところを取ったのがミニバッチです。
ミニバッチとはランダムにいくつかのグループに学習データを分け、並列に学習する方法。
それぞれの学習データのグループから損失の平均を計算し、それをもとに学習します。
グループごとに損失関数が若干異なるので局所解にハマりにくく、良い解にたどり着きやすくなります。
また並列計算ができるので計算を行うGPUとの相性が良いです。
学習時の注意:overfitting(過学習)
次に学習するにあたっての注意点、過学習です。
過学習とは学習用データに適合しすぎて、テストデータに適合できなくなってしまう問題です。
過学習が起きる理由としまして
1.モデルの自由度が高い(ニューロンの数が多い),特徴量が多い
2.データ数が少ない
3.ノイズ、外れ値が多い
それぞれの項目に対して対策があります。3.については後述する初期値の設定方法でお話します。
1.モデルの自由度が高い対策
モデルにノイズ追加
学習をあえて邪魔をしてより強いモデルを作る手法です。
例えばトレーニングの時、重りをつけて、試合の時に重りを外して本気を出すスポーツ選手みたいなイメージでしょうか。
Dropput
↑の一例、学習時にランダムにNNの一部のノードを一時的に無効化する手法。
L1,L2正則化
損失関数に正則化項を入れて対応します。
式にすると以下のように
$$
E=E_0+\lambda E_w(w)
$$
で、正則化にも
L1正則化(Lasso)
L2正則化(Ridge)
があり,$E(w)$が異なります。
L_1:E_w(w)=\sum_{k=1}^{n} |w_k| \\
L_2:E_w(w)=\sum_{k=1}^{n} |w_k|^2
Early Stopping
正則化が十分でない場合、テストデータに対する誤差が増えてしまう場合があります。
そこで学習が進んでテスト誤差が増える前に学習を止めてしまう手法をEarly Stoppingと言います。
スパース表現
L1では重みwがスパース、つまり0になったりします。L2 の場合、0.00001のように小さな値が残りやすいです。
なのでL1では特徴量選択、計算メモリ少なくすみます。
2.データ数が少ない対策
Deep Augmentation
学習データを水増しする手法。画像データなら
・左右反転
・上下反転
・回転
・前後左右への移動
・拡大縮小
・色の変換
が挙げられます。
ドメイン固有の知識が必要でないとできないので注意。
半教師あり学習
教師データをもとに教師なしデータを分類してから学習する方法です。
大量に教師ありデータを得るのは難しいけど、ないものなら入手できるから自分たちでデータ作っちゃおうという発想。
学習時の注意:初期値の設定方法
下図のようによい初期値からスタートすればより早く良い解に到達する確率が高まります。
一例としましては
He初期化(RelUの場合)
Xavier初期化(点対象の活性化関数の場合)
があります、次によい解にたどり着くにはどうしたらよいかご紹介します。
正規化
データを前もって扱いやすい形に変換します。
例えば特徴の値を-1~1に収めたり、後述する白色化だったり様々な手法があります。
標準化
データの値をx,平均をμ、標準偏差をσとすると
$$
Z=\frac{x-\mu}{\sigma}
$$
とデータに前処理をし、平均は0、標準偏差は1の標準正規分布にします。
無相関化
特徴量に相関がないようデータを回転させる前処理。
データがy=axのグラフで近似できているものをy=0の式で近似できるよう変換するイメージです。
白色化
無相関化+標準化。データの収束が早くなります。
Batch Normalization
Batch Normalizationは各バッチごとに白色化をかけ、各層ごとに平均0,分散1にする正規化を施します。
層を重ねると正規化や白色化の効果が薄れる場合があり、これを共変量シフトといいます。Batch Normalizationではこの共変量シフトを解消しています。
この派生形でLayer Normalization(chで正規化)、Instance Normalization(ch独立で画像で正規化)があります。
教師あり事前学習
Batch Normalizationが登場したのでほぼ使わなくなった手法。Dropoutの層バージョン。
層1,層2,層3があるとします。
まず層1を学習させた後、層1の学習を止めた状態で層2と一緒に学習します。
その後層1,2の学習を止めたまま層3を追加し、ガキ収支、最後にすべての層を一度に学習させる手法です。
使われていませんが、事前に簡単な問題を学習させ、その後本当にやりたい問題を学習すると性能が良くなるというテクニックは現在も使われています。
マルチタスク学習
いくつかの問題を1つのネットワークで同時に解く手法。
自動運転だったら、どこに何があるかという問題とそれがどのくらいのスピードで動いているかを同時に1つのNNで解くイメージです。
性能向上が期待できます。
アンサンブル学習
学習機を複数掛け合わせて良い解を導く手法です。
バギング
弱いモデルを複数用意し、多数決を取る手法
多様なNNを用意するのがポイント。
ブースティング
学習機を用意し、その学習機が間違えた問題に対する学習機を用意し、その学習機を・・・
と直列に学習機をつなげる手法、時間はかかりますが汎化性能が上がります。
今日はここまで。