やっと分かった気がしてきたので書きます。
ベイズの定理とは
ある事象$H$が起きた条件下で$D$が起きる確率を以下の式で表せます。
$$
P(D|H)=\dfrac{P(H|D)P(D)}{P(H)}
$$
D:Distrbution(分布)
H:Hypothesis(仮定)
明確な文献を見つけられなかったのですがDとHはこの略だと推定しています。
つまりどういうことだってばよ
ベイズの定理は読解力も試されます。
こんな問題を考えましょう。
ジョーカーを抜いたトランプの山札があります。一枚カードをとったとき、それがダイヤでかつ絵札である確率は?
ちなみに図の斜線部の確率です。
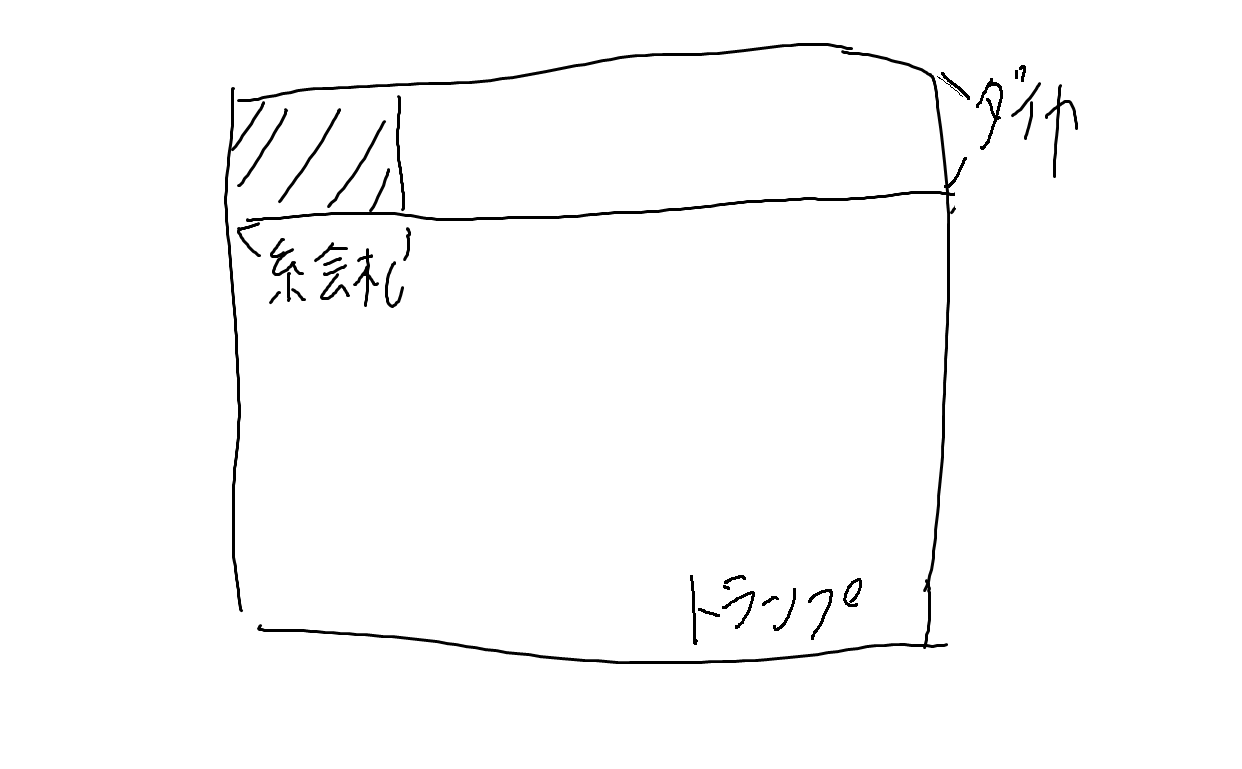
ダイヤでかつ絵札は全部で3枚しかないので答えは$\frac{3}{52}$
では次の問題
ジョーカーを抜いたトランプの山札があります。一枚カードをとったとき、それが絵札でかつダイヤである確率は?
図の斜線部の確率です。
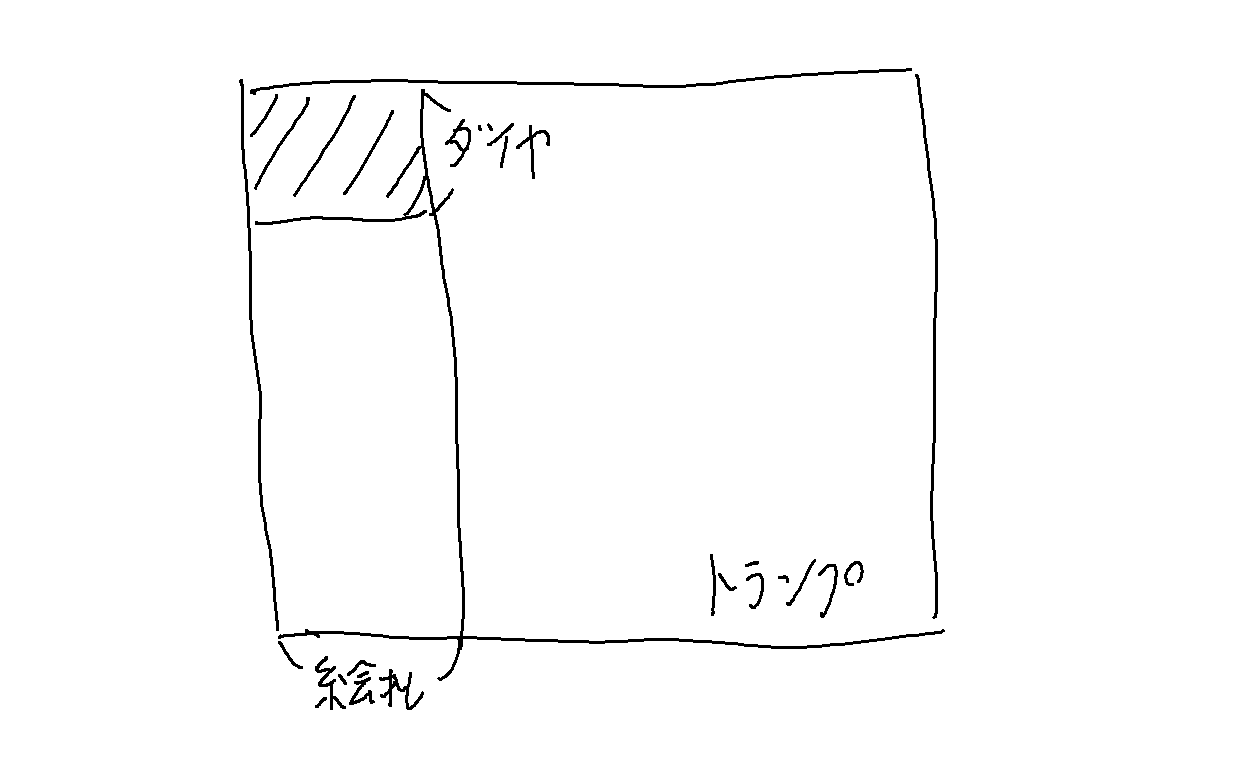
絵札でかつダイヤは全部で3枚しかないので答えは$\frac{3}{52}$
つまり
引いたカードがダイヤである確率×引いたカードがダイヤであったときに絵札である確率
=引いたカードが絵札である確率×引いたカードが絵札であったときダイヤである確率
と言えます。
この式をベイズの式にあてはめます。
$P(H)$:引いたカードがダイヤである確率
$P(D)$:引いたカードが絵札である確率
$P(H|D)$:引いたカードが絵札だった時、ダイヤである確率
$P(D|H)$:引いたカードがダイヤだったとき、絵札である確率
DとHは問題によって変化するので今回はお気になさらなず。
とすると
$$
P(D|H){P(H)}={P(H|D)P(D)}
$$
変形すると
$$
P(D|H)=\dfrac{P(H|D)P(D)}{P(H)}
$$
ベイズの公式の完成。
例題
ジョーカーを抜いたトランプの山札があります。一枚カードをとるとそのカードのマークはクラブでした。この時カードが絵札である確率は?
Hは仮説なので
$P(H)$:引いたカードがクラブである確率
です。順次公式に当てはめていきましょう。
$P(D)$:引いたカードが絵札である確率
$P(H|D)$:引いたカードが絵札だった時、クラブである確率
$P(D|H)$:引いたカードがクラブだったとき、絵札である確率
では計算すると
$$
P(D|H)=\frac{P(H|D)P(D)}{P(H)}=\frac{\frac{1}{4}\frac{4}{13}}{\frac{1}{4}}=\frac{4}{13}
$$
こんな感じです。
参考文献
図解・ベイズ統計「超」入門 (サイエンス・アイ新書)