More than 3 years have passed since last update.

ホテリングのT^2法による多変量正規分布を仮定した異常検知

Last updated at 2020-06-30Posted at 2020-06-30

はじめに

本連載について

こんにちは，(株)日立製作所 Lumada Data Science Lab. の露木です。

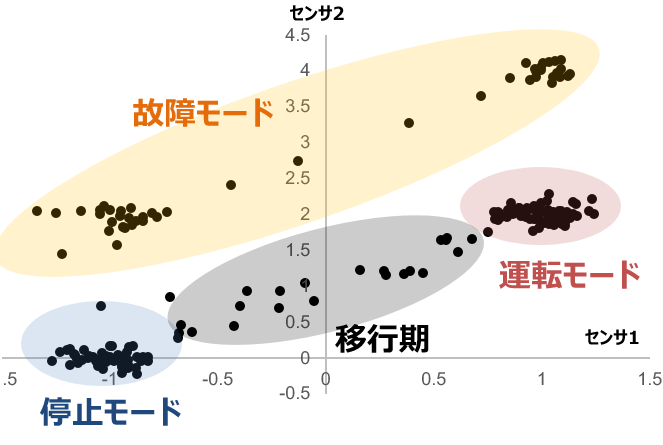
化学プラントや工場設備，あるいはもっと身近なモーターや冷蔵庫などの故障予兆検知を行う際に，振動や音，温度，圧力，電圧，消費電力のような値を取得できる複数のセンサーで測定した多次元の時系列数値データを分析することがあります。このような故障予兆検知は，機械学習の分野では異常検知問題として解くことができます。

そこで本連載では時系列数値データの異常検知を題材とし，数回の記事に分けてアルゴリズムの基礎的な説明と実装を示していきます。

第1回. scipyを使って特徴量の相関を考慮したマハラノビス距離を計算する
第2回. ホテリングの$T^2$法による多変量正規分布を仮定した異常検知
第3回. GMMによる多峰性分布にもとづいたデータの異常検知
第4回. 移動窓を使った多次元時系列データの異常検知

今回扱う内容: ホテリングのT^2法

今回は「ホテリングの $T^2$ 法」による異常検知を紹介します。ホテリングの $T^2$ 法は，アメリカの経済学者ハロルド・ホテリングが確立した古典的な手法です ¹ ² ³ ⁴ 。この異常検知技術は初回の記事で説明したユースケースに必要な4つの要素技術のうち 2. に相当します。

時系列数値データの異常検知に必要な4つの要素技術
- 要素技術1. 特徴量空間における距離の定義
- 要素技術2. 正常データの分布を仮定し，異常なデータと正常なデータを分ける閾値を設定する方法 (本稿)
- 要素技術3. 複数のモードに対応できるクラスタリング
- 要素技術4. 時系列データに対応するための移動窓の活用

この2.の要素技術をさらに分解すると以下の4つの手順に細分化できます。本記事では以下の手順のそれぞれについて説明を加えながら実装の紹介を行います。

手順1. 母集団の分布を推定する: 統計量として標本の平均値と分散共分散行列を計算する
手順2. 異常度を計算する: 標本ごとにマハラノビスの2乗値を計算する
手順3. 閾値を計算する: 所望の異常検知確率から異常度の閾値を逆算する
手順4. 異常を判定する: 異常度が閾値より大きい場合は異常と判定

データセットの準備

実際のデータを測定すると時間がかかりますから，ここでは人工的なデータセットを作成して異常検知技術を試します。初回の記事で説明した異常検知のユースケースにもとづけば，図1における各モードに応じた4つ程度の正規分布を作るべきといえます。

図1. 期待される分析結果

一方で，ホテリングの$T^2$法の理論では母集団が1つの正規分布に従うことを仮定します¹²³⁴。そこで，本記事ではクラスタリング等の何らかの手段によって「図1の運転モードに相当するデータだけ分離できた」と仮定して2次元の正規分布に従ったデータセットを作成することにします。

正規分布は平均$\mu$と分散$\sigma$の2つのパラメータで定義される確率分布ですので，それらの値を設定すればデータセットを作成できます。ただし，今回は2次元の正規分布を作りたいので分散はスカラーではなく行列 (分散共分散行列 $\Sigma$) になります。この分散共分散行列はその対角項に分散，非対角項に共分散 (次元間の相関を表す行列要素) を含む行列です。

実装

以下のコードでは平均 $\mu = (0,0)$ と分散に 50, 共分散に 35 の値を設定し，念のため多めに10万点のデータセットを作成します。データ数は，後に計算する標本の平均と分散共分散行列の精度が十分に高くなる程度の数があれば良いので，必ずしも10万点も必要とは限りません。

python

import matplotlib.pyplot as plt
import numpy as np

# 2次元の正規分布からデータセットを作成する
mean = np.array((0,0)) # 平均値をゼロに設定
cov = np.array([(50, 35), (35, 50)]) # 分散共分散行列を設定

# データを10万点作成する
X = np.random.multivariate_normal(mean, cov, 100000)

可視化

このデータセットを可視化すると図2のようになります。先程のコードでは分散共分散行列を表す変数 cov で 35 という比較的大きな共分散を指定していますので，右肩上がりのような相関を持った2次元の正規分布となっています。

python

# データセットの分布を可視化
plt.plot(X.T[0], X.T[1], 'x', alpha=0.01)
plt.axis('equal')
plt.show()

図2. データセットの分布

異常検知の実装

手順1. 母集団の分布を推定する

実装

作成したデータセット (母集団) から，その分布を推定します。具体的には，標本の平均${\bf \hat \mu}$と分散共分散行列 $\hat \Sigma$ を計算することで，元になっている正規分布の形状を明らかにします。この計算はホテリングの$T^2$法において異常度として用いる「マハラノビス距離の2乗値」を求めるために必要な準備です。

python

# 標本の平均を計算
mu = X.mean(axis=0)
# 標本の分散共分散行列を計算
cov2 = np.cov(X.T)

可視化

念の為，計算結果を真値 (母集団の平均と分散共分散行列) と比較すると，平均については 0 であるべきところを -0.00602358，分散については 50 であるべきところを 50.18772103 などと比較的良く推定できていることがわかります。

python

print("母集団の平均")
print(mean)
print("標本平均")
print(mu)

print("\n母集団の分散共分散行列")
print(cov)
print("標本による分散共分散行列")
print(cov2)

実行結果

母集団の平均
[0 0]
標本平均
[-0.00602358  0.00186333]

母集団の分散共分散行列
[[50 35]
 [35 50]]
標本による分散共分散行列
[[50.18772103 35.14373908]
 [35.14373908 49.97181938]]

手順2. 異常度を計算する

次に標本 ${\bf x'}$ の異常度 $a({\bf x}')$ を計算します。ホテリングの$T^2$法では，式(1)で計算できる「標本$\bf x'$と標本平均$\bf \hat \mu$ の間のマハラノビス距離の2乗値」を異常度として用います。マハラノビス距離は前回の記事で説明したように，母集団の分散を考慮した距離の定義方法です。一般的なユークリッド距離の代わりに，マハラノビス距離を使うことで特徴量間に強い相関がある場合でも正常データと異常データを分離しやすくなる利点があります。

a({\bf x}') \equiv({\bf x'} - {\bf \hat \mu})^{\rm T} {\hat \Sigma^{-1}} ({\bf x'} - {\bf \hat \mu}) \tag{1}

実装

式(1)の標本平均$\hat \mu$や標本の分散共分散行列 $\hat \Sigma$は，先程の手順1で計算済みです。したがって，例えば(1,1) の特徴量を持つ標本の異常度は以下のコードで計算できます。

python

from scipy.spatial import distance
from scipy.stats import chi2

# 分散共分散行列の逆行列を計算
cov_i = np.linalg.pinv(cov2)

# 異常度を計算したい点を設定
x = (1, 1)

# 異常度を計算 (マハラノビス距離の2乗値を計算)
anomaly_score = distance.mahalanobis(x, mu, cov_i)**2

# 異常度を表示
print("異常度 = %.2f" % anomaly_score)

実行結果

異常度 = 0.02

なお，先に作成したデータセットの全データについて異常度を計算する処理は，Pythonのリスト内包表記を使って以下のように書けます。

python

# データセット (変数X) に含まれる全データについて異常度を計算
anomaly_scores = np.array([x for x in X if distance.mahalanobis(x, mu, cov_i)**2])

手順3. 閾値を計算する

異常度が計算できたら，次は異常検知のための閾値を設定します。マハラノビス距離と正規分布の性質から，式(1)で定義される異常度は「特徴量の次元 (自由度) $m$ に対してデータ数$N$が十分に大きい」とき，近似的に自由度$m$のカイ二乗分布に従うことが知られています³ ⁴ 。これは異常データが検知される確率から，異常度の閾値を逆算できることを意味します。

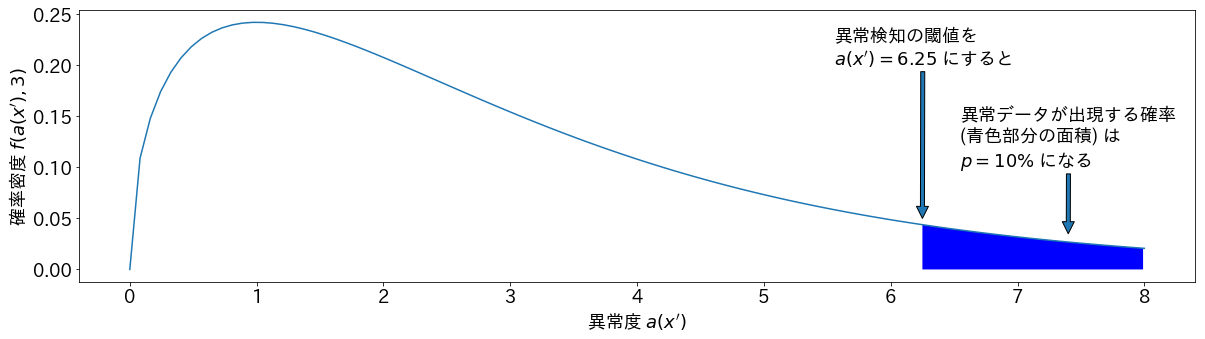
例えば自由度$m=3$のとき，異常データの数を全体の10％に設定したい場合は

\int^\infty_{6.25} f(a,3) {\rm d}a = 1 - \int^{6.25}_0 f(a,3) {\rm d}a = 0.10  \tag{2}

であるので，異常度 $a({\bf x}')= 6.25$ を閾値に設定すれば良いと逆算できます。ただし，$f(a,m)$はカイ二乗分布の確率密度関数です。

この閾値と異常検知確率の関係は図3のように可視化できます ⁵ 。図3の縦軸は自由度3のカイ二乗分布の確率密度を表しており，横軸は異常度です。先程の例のように横軸の異常度 $a({\bf x}')= 6.25$ を閾値として設定すれば，異常データが出現する確率 (青色部分の面積) は全体の 10% になります。

クリックして描画コードを開く

ソースコード

import matplotlib.pyplot as plt
import matplotlib as mpl
from scipy.stats import chi2
import numpy as np

# 日本語フォント設定
font = {'family':'IPAexGothic'}
mpl.rc('font', **font)

# 自由度
m = 3

plt.rcParams["font.size"] = 18
plt.figure(figsize=(20,5))

# カイ二乗分布の確率密度関数を可視化
chi_pdf = np.array([(x, chi2.pdf(x, m)) for x in np.linspace(0, 8, 100)])
plt.plot(chi_pdf[:,0], chi_pdf[:,1])

x1 = np.arange(6.25, 8, 0.01)
y1 = chi2.pdf(x1, m)
y2 = np.zeros(x1.shape)
plt.fill_between(x1, y1, y2, where=y1>y2, facecolor='blue')
plt.annotate("異常検知の閾値を\n$a(x')=6.25$ にすると",
             xy=(6.25, 0.05), xytext=(5.55, 0.20), arrowprops=dict())
plt.annotate("異常データが出現する確率\n(青色部分の面積) は\n$p=10\%$ になる",
             xy=(7.4, 0.035), xytext=(6.55, 0.1), arrowprops=dict())
plt.xlabel("異常度 $a(x')$")
plt.ylabel("確率密度 $f(a(x'), %d)$" % m)

plt.show()

図3. 自由度3のカイ二乗分布の確率密度関数と異常検知される確率の関係

実装

PythonのScipyライブラリでは，式(2)の積分の逆関数は scipy.stats.chi2.isf() の関数として提供されています。したがって，以下のコードで閾値を計算できます。

python

m = 3    # 自由度 (特徴量の次元) を設定
p = 0.1  # 異常検知される確率を設定
threshold = chi2.isf(p, m)  # 異常検知の閾値を計算

print("自由度 %d で異常検知される確率を %1.2f %%に設定したければ，閾値は %1.2f" % (m, 100 * p, threshold))

実行結果

自由度 3 で異常検知される確率を 10.00 %に設定にしたければ，閾値は 6.25

可視化

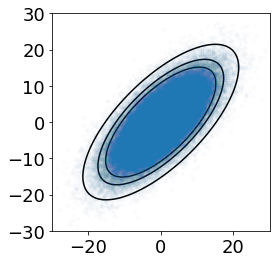
参考までに，異常度の閾値を等高線図として可視化した結果を図4に示します。図4の等高線は，内側からそれぞれ異常検知される確率を10%，5%，1%に設定した場合を表しています (これら確率の値は理解を深めるための例示であり，実用上の意味があるものではありません)。ホテリングの$T^2$法に従って異常検知を行う場合，これらの等高線よりも外側にある標本を異常と判定することになります。

python

# 可視化したい「異常検知される確率」の値を設定
probs = [0.1, 0.05, 0.01]

# 確率に対応する等高線の値を計算
levels = [chi2.isf(x, X.shape[-1]) for x in probs]

# 表示範囲の指定
r = 30

# z軸値(異常度)を計算
z = np.array(
    [
        [(i, j, distance.mahalanobis([i,j], mu, cov_i)**2)
         for i in np.linspace(-r, r, 100)]
         for j in np.linspace(-r, r, 100)]
)

# グラフ描画
myfig = plt.figure()
myax = myfig.add_subplot(1, 1, 1)
myax.set_aspect('equal')
plt.ylim(-r, r)
plt.xlim(-r, r)

# 等高線図を描画
cont = plt.contour(z.transpose()[0], z.transpose()[1], z.transpose()[2], levels=levels, colors=['k'])

# 散布図の描画
plt.plot(X[:,0], X[:,1], '.', alpha=0.01)
plt.show()

図4. 異常検知される確率と正常データの範囲。等高線は内側から10%，5%，1％の標本が異常として検知される場合に対応する

手順4. 異常を判定する

実装

閾値を使って異常判定する方法を示します。この判定はif文で，手順2の異常度と手順3の閾値について大小関係を比較するだけで簡単に実装できます。

python

if anomaly_score > threshold:
    print("このデータは異常です")

また，データセットに含まれるすべての標本について異常判定する場合は，以下のようにリスト内包表記で記述すると異常度の計算から判定まで1行で行えるので便利です。

python

anomaly_data = np.array([x for x in X if distance.mahalanobis(x, mu, cov_i)**2 > threshold])

可視化

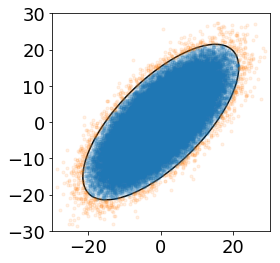
ここまでに紹介したコードを使って，異常検知される確率を1%とした場合の異常検知を行い，散布図で可視化します。1%という数値は仮に選択したものですが，実際にはユースケースに応じて定めます。つまり，異常データを見逃さないこと (あるいは何％の確率なら見逃しても許容されるか) といった要件や，例えば観測されるデータが1ヶ月で10万件あったとして，その1%に相当する1000件が異常として検知されたとき，1000件/月の詳細を確認する人員数を確保できるのか？といった案件固有の事情を加味しながら総合的に判断します。

この可視化は以下のPythonコードで実現でき，実行結果として図5を得ます。図5中のオレンジ色のプロット点が，異常と判定された標本を示します。等高線図の外側の出現確率の低い (具体的には1%以下の) 標本が異常と判定されていることがわかります。

python

# 異常検知の実施
##  異常検知される確率を1%に設定
p = 0.01

## 確率に対応する異常度の閾値を計算
threshold = chi2.isf(p, X.shape[-1])

## データセットについて異常検知を実施
anomaly_data = np.array([x for x in X if distance.mahalanobis(x, mu, cov_i)**2 > threshold])

## 可視化用に正常データのみを含むリストも作る
normal_data = np.array([x for x in X if distance.mahalanobis(x, mu, cov_i)**2 <= threshold])

# 散布図として異常検知結果を可視化する
## 表示範囲の指定
r = 30

## z軸値(異常度)を計算
z = np.array(
    [
        [(i, j, distance.mahalanobis([i,j], mu, cov_i)**2)
         for i in np.linspace(-r, r, 100)]
         for j in np.linspace(-r, r, 100)]
)

## グラフ描画
myfig = plt.figure()
myax = myfig.add_subplot(1, 1, 1)
myax.set_aspect('equal')
plt.ylim(-r, r)
plt.xlim(-r, r)

## 等高線図を描画
cont = plt.contour(z.transpose()[0], z.transpose()[1], z.transpose()[2], levels=[threshold], colors=['k'])

## 散布図の描画
plt.plot(normal_data[:,0], normal_data[:,1], '.', alpha=0.1)
plt.plot(anomaly_data[:,0], anomaly_data[:,1], '.', alpha=0.1)
plt.show()

図5. 異常検知結果

異常検知結果の検算

最後に，実際に異常検知された確率 (実績値) が閾値設定時の想定 (設定値) と一致するか検算します。この検算が合わない場合は母集団の分布を正しく推定できていないことが示唆され，原因として以下のような可能性を考えることができます。

母集団が単一の正規分布に従わない可能性
- 対策: 収集したデータセットの可視化などを行って分布を確認します。そのうえで，前処理の工夫やホテリングの$T^2$法以外のアルゴリズムの採用を検討します。
標本平均・標本分散の推定が誤っている可能性
- 対策: データ収集を継続してデータセットの標本数を増やします。
診断対象のデータ数が少なすぎる可能性
- 対策: 診断対象のデータ数を増やして再度検算を行います。

今回の例であれば，以下のように異常検知確率の設定値 1.00% に対して実績値 0.99% となり，ほぼ一致します。これは「データセットの準備」の章で単一の正規分布から十分に多い標本数を作成しており，ホテリングの$T^2$法の仮定を満たすデータセットであるからです。

python

print("異常検知された標本数: %10d個" % len(anomaly_data))
print("異常検知確率 (設定値): %10.2f%%" % (p * 100))
print("異常検知確率 (実績値): %10.2f%%" % (len(anomaly_data)/len(X) * 100))

実行結果

異常検知された標本数:        988個
異常検知確率 (設定値):       1.00%
異常検知確率 (実績値):       0.99%

おわりに

本記事では，ホテリングの $T^2$ 法の手順を追いながら，その考え方と実装を示しました。ホテリングの$T^2$法による異常検知は理論的に明確で扱いやすいですが，何度も述べているように母集団が単一の正規分布に従う強い仮定を求めます。しかし，実世界の異常検知問題では複数の状態を背景に持ち，単一の正規分布ではうまく表現できない系を扱うことも少なくありません。

このような場合は，k-means法や混合正規分布モデル(GMM)によるクラスタリングや，1クラスサポートベクトルマシンといった別のアルゴリズムの利用も検討しなければなりません³ 。そこで，次回の記事ではGMMを使って多峰的な正規分布 (複数の正規分布) にもとづいたデータの異常検知を行う方法を示します。

参考文献

NIST/SEMATECH. "Hotelling T Squared." §6.5.4.3 in NIST/Sematech Engineering Statistics Internet Handbook. . ↩ ↩²
Hotelling, H. Multivariate Quality Control. In C. Eisenhart, M. W. Hastay, and W. A. Wallis, eds. Techniques of Statistical Analysis. New York: McGraw-Hill, 1947. ↩ ↩²
井手, 入門機械学習による異常検知 Rによる実践ガイド, コロナ社, 2015. ↩ ↩² ↩³ ↩⁴
Hotelling's T-squared distribution - Wikipedia ↩ ↩² ↩³
scipy.stats.chi2 ? SciPy v1.4.1 Reference Guide ↩

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up