山田太郎vs山本太郎にみるベイズ統計vs頻度論

本記事では，2019年に行われた参院選挙で起きた集計ミスを題材にベイズ統計とその実装例を紹介するものである．データは@PokersonTさんが公開しているものを用い，分析の方針は東工大の下平教授（@hshimodaira）の解析に従った．基本的には下平教授の研究室にRで公開されている分析と同じ内容をPythonで実装しつつ，ベイズ統計の説明を加えたものである．特に，本記事はベイズ統計を用いた時に得られる結果が頻度論を用いた場合と比較して，どのように/なぜ異なるのか，という点に強調を置いている．

（執筆中です）

問題の背景：参院選と集計ミス問題

第25回参議院議員通常選挙

第25回参議院議員通常選挙は、2019年（令和元年）7月21日に投開票された参議院議員通常選挙である．本選挙では，長期政権となった安倍政権（参院選時は第4次安倍改造内閣）への評価だけでなく，旧民主党が立憲民主党と国民民主党に分裂してから最初の参院選でありそれぞれの政党の力量や，さらに，「れいわ新選組」や「NHKから国民を守る会」といった新しい政治団体の行動にも関心が集まった．また，新しく導入された特定枠制度により，れいわ新選組から身体に重度の障害をもつ舩後靖彦氏と木村英子氏が当選したことも話題となった．一方で，争点が明確でなかったことや，参院選への報道が直前に発生した京都アニメーション放火事件や吉本闇営業事件の報道のために減ったこともあり，投票率は48.8％と史上2回目の投票率50%を割り込む事態となった．

山田太郎->山本太郎の集計ミス問題の発覚

上記のような参院選の開票後に話題になったのは静岡県富士宮市で山田太郎氏の票が山本太郎氏に集計されてしまった問題である．集計ミスは山田氏に投票した市民らが山田氏の得票数が0になっていることを気づき選挙管理に問い合わせたことなどにより発覚した．その後の調査で，山田氏の得票全515票を山本氏に誤って計上していたことが判明した（当落への影響はなかった）．

Twitter上で示された分析結果

ネット上でもこの集計ミスは話題となった．Twitter上では山田氏と山本氏の得票結果を並べて比較し，山田氏の得票数が異常に低いことを指摘する一方で，東工大の下平教授（@hshimodaira
）はベイズ統計を用いた仮説検定によって他の市でも集計ミスがある可能性を示した．

上越市で82票っていうのがどのくらいヤバいかを計算してみた．上越市でこんな得票数になる確率は百万回に８回くらいでほぼあり得ない．他の市は最低でも１５％で普通．ただし，どの市も同じような性質と仮定してbeta-binomial分布を仮定して計算． https://t.co/xHn7jxf04l pic.twitter.com/MS1UDBEREg

— はかせ Mk-II @ 高度AI人材 (@hshimodaira) July 24, 2019

上越市では集計に間違いはないとしており，本記事執筆時点で本当に集計ミスがあったのかどうかは定かではないものの，このTwitter上での分析は統計解析の実問題を解決するための応用例として注目を集めた．なお，下平教授は[研究室のホームページ](http://stat.sys.i.kyoto-u.ac.jp/post-ja/844/)で分析結果と分析に用いたソースコード（R）を公開している．

ベイズ統計とPythonによる集計ミスの統計解析

本記事では，下平教授が行った結果をPythonで再現するとともに，今回の集計ミス問題を通じてベイズ統計の解説や頻度論に基づくアプローチとの比較を行う．最初に一般的な二項分布に従うデータに対するベイズ統計の枠組みを紹介した後に，次にベイズ統計に基づくPythonでの実装例を示し，最後にその結果について議論する．

ベイズ統計の基礎

ベルヌーイ試行と二項分布

データ$y_1, y_2,..., y_n$に対してベルヌーイ試行を考える．つまり，$i=1,2,...,n$に対して$y_i$が$0$，もしくは$1$を取るものとする．ここで，$y_i$が$1$となる確率を$\theta$とすると，$y=\sum^n_iy_i$なる$y$はパラメータ$\theta$を持つ二項分布に従う．つまり，$y$が従う確率密度関数は，
$$P(y|\theta)=Bin(y|n,\theta)=\begin{pmatrix}
n \\
y
\end{pmatrix}\theta^y(1-\theta)^{n-y}$$
となる．

二項分布に対する事前分布

二項分布のパラメータ$\theta$を確率変数であると考えて，その分布に対する事前分布を考える．$n$回の施行のうち$1$が出た回数を$a$，$0$が出た回数を$b$とする．尤度をデータを与えた下でのパラメータ$\theta$の関数として表すと
$$P(y|\theta)\propto\theta^a(1-\theta)^b$$
となる．このように，事前分布が尤度と同じ形をしているのであれば，事後分布もそれに対応する形になる．そのような事前分布を
$$p(\theta)\propto \theta^{\alpha-1}(1-\theta)^{\beta-1}$$
とする．これは$\alpha$と$\beta$をパラメータにもつベータ分布である．つまり，
$$\theta \sim Beta(\alpha,\beta).$$
この事前分布のハイパーパラメータ$\alpha$と$\beta$は，$\alpha-1$回の成功と$\beta-1$回の失敗が事前に与えられていることを意味している．
適当な$\alpha$と$\beta$のもとで，$n$回の試行のうち$y$回成功したという情報が得られると，その情報のもとでの事後分布は
$$p(\theta|y)\propto\theta^y(1-\theta)^{n-y}\theta^{\alpha-1}(1-\theta)^{\beta-1}=Beta(\theta|\alpha+y, \beta+n-y)$$
となる．このように事後分布が事前分布と同じ形になるという性質は共役性と呼ばれている．ベータ分布は二項分布に対して共役性をもつ事前分布の仲間のうちの１つである．共役性をもつ事前分布（共役事前分布）は事後分布を解析的に（つまりMCMCのようなコンピュータを使ったシミュレーションのような計算などを必要とせずに）得ることができるので，分析する人にとって扱いやすい．

ベータ分布を事前分布に持つ場合の事後分布の期待値と分散

前節で紹介した事後分布
$$p(\theta|y)\propto\theta^y(1-\theta)^{n-y}\theta^{\alpha-1}(1-\theta)^{\beta-1}=Beta(\theta|\alpha+y, \beta+n-y)$$
の期待値と分散を求めることにする．これはベータ分布の期待値と分散の式に基づけば
$$E(\theta|y)=\frac{\alpha+y}{\alpha+\beta+n},\ \ \ var(\theta|y)=\frac{(\alpha+y)(\beta+n-y)}{(\alpha+\beta+n)^2(\alpha+\beta+n+1)}$$
として得られる．$y$と$n-y$が大きくなれば，$E(\theta|y)$と$var(\theta|y)$は，それぞれ$E(\theta|y)\approx y/n$と$var(\theta|y)\approx\frac{1}{n}\frac{y}{n}(1-\frac{y}{n})$と近似できる．つまり，サンプルサイズが大きくなれば事前分布の影響はなくなるのである．

階層ベイズ

執筆中．

Pythonによる分析

MCMCをPythonで行う際のライブラリの候補には，PyMCとPyStanがある．本稿では，$n$個のサンプル${(n_i, y_i)}^n_{i=1}$PyMCを用いて，階層ベイズモデル
$$\lambda \sim Uniform(0,1)$$
$$\phi \sim Uniform (0.1, 10000)$$
$$\alpha = \lambda\phi$$
$$\beta = \lambda(1-\phi)$$
$$\theta \sim Bata(\alpha, \beta)$$
$$y_i \sim Bin(y|n_i, \theta)\ \ \ for\ \ \ i=0,1,...,n$$
を推定する．

データの説明と読み込み

データはTwitter上で@PokersonTさんが公開しているものを用いた．

数字データも貼っておきます

エクセルのデータが欲しい人はここから持って行ってくださいhttps://t.co/q82phisB3O pic.twitter.com/AZAXFqlE83

— 梅酒みりん⋈ 9~12C96 (@PokersonT) July 23, 2019

これをpandasを用いて

df_votes = pd.read_excel('新潟県得票数.xlsx', usecols=[2, 3, 4], skiprows=[0,1,2], index_col=0, names=['Total　Votes', 'Yamada Votes'])

のように読み込む．最初の5行を表示すると

df_votes.head()

となる．また，投票数と得票数の関係を散布図で表すと　

df_votes = pd.read_excel('新潟県得票数.xlsx', usecols=[2, 3, 4], skiprows=[0,1,2], index_col=0, names=['total_votes', 'yamada_votes'])

となる．

階層ベイズモデルのパラメータの推定

次にMCMCを用いて階層ベイズモデルのパラメータを推定する．市町村のインデックスを$i=0,1,...,36$として，それぞれを新潟市，上越市，．．．，出雲崎町を対応させる．それにより，各市町村に対応する二項分布のパラメータを$p0,p1,...,p36$とする．

data = np.array(df_votes.values, np.int)
num_of_iter = 20000
burn_in = 20000

with pm.Model() as model:
    #モデルの定義
    lmbd =  pm.Uniform('lmbd', 0.1, 10000)
    phi = pm.Uniform('phi', 0, 1)
    alpha = lmbd*phi
    beta = lmbd * (1-phi);
    for i in range(len(data)): 
        #上越市のデータは用いない．
        if i != 1:
            p = pm.Beta('p%d'%i, alpha=alpha, beta=beta)
            y = pm.Binomial('y%d'%i, n=data[i,0], p=p, observed=data[i,1])
    #推定（MCMC)
    step = pm.Metropolis()
    trace = pm.sample(20000, tune=burn_in, chains=2)

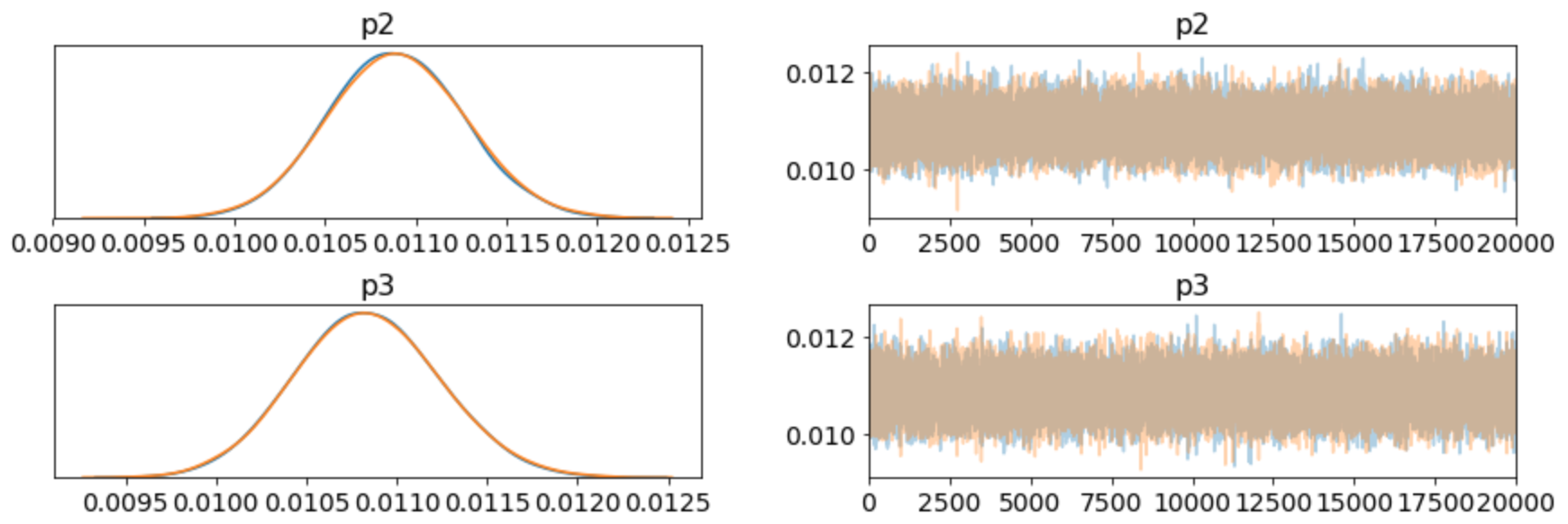
ここで推定した結果をtraceplotを用いて以下のように表せる．　

pm.traceplot(trace)
plt.savefig('fig.jpeg')

山田太郎氏の得票率の検定

執筆中

ベイズ統計vs頻度論

頻度論に基づきパラメータを推定する．尤度関数を以下のように定義する．

def likelihood(theta, n, x):
    logliklihood = np.log((theta**x)*((1-theta)**(n - x)))
    value = np.sum(logliklihood[logliklihood > -np.inf])/len(logliklihood)
    return value

この尤度関数を最大化するパラメータを求める．

from scipy.optimize import minimize

func = lambda theta: -likelihood(theta, nx[:, 0], nx[:, 1])

values = []
num_of_iter = 10000
for i in range(num_of_iter):
    values.append(func(i/num_of_iter))
    
opt_p = np.argmax(values)/num_of_iter

この時，最尤推定量は$0.1026$となる．この推定量を尤度比検定で上越市の$0.00095$で棄却できるか否かを考える．

from scipy.stats.distributions import chi2

#https://stackoverflow.com/questions/38248595/likelihood-ratio-test-in-python
def likelihood_ratio(llmin, llmax):
    return(2*(llmax-llmin))


n0 = np.array([df_votes[df_votes.index == '上越市'].values[0][0]])
x0 = np.array([df_votes[df_votes.index == '上越市'].values[0][1]])

L1 = func(x0/n0)
L2 = func(opt_p)

LR = likelihood_ratio(L1,L2)

p = chi2.sf(LR, 1)

print('p: %.30f' % p)

p値は$0.000000000000000000011$となる．

結論