先日某社で2週間の短期インターンシップに参加してきました。
内容としては製造ラインで行われる外観検査をディープラーニングを用いて自動化することを想定して、画像から不良を検出するモデルを作成するというものでした。
そこでmetric learningについて少し勉強し、"L2-constrained Softmax Loss for Discriminative Face Verification"という論文を読んだので内容をまとめたいと思います。
嘘ついてるかもしれないので気をつけて読んでもらえると助かります。
metric learningとは?
metric learningとはデータ間の関係を計量を用いて表現する特徴空間への変換を学習する手法です。図のようにニューラルネットワークを用いて同じクラスのデータは近くに、違うクラスのデータは遠くなるように特徴空間へデータの埋め込みを行います。学習によって得られたネットワークを用いてデータの変換を行い、得られた特徴ベクトル間の距離を求めることでそのデータがそのクラスに属するか、属さないか判定することができます。

異常検知では異常とされるデータ数が少なかったり、学習セットに全ての異常パターンが含まれているとは限らないといった問題があるため、metric learningを用いて正常サンプルの"正常さ"を学習し、新しい入力データと正常サンプル間の距離から適当な閾値で同一かどうか判断することで異常を検出します。
異常検知以外にも顔認識でよく用いられるみたいです。
Triplet Loss
metric learningにおける代表的な損失関数としてTriplet Lossが挙げられます。
TensorFlowやPyTorchといった有名なディープラーニングフレームワークには実装されているので、簡単に使うことができます。
Triplet Lossは次式のとおりです。
L(a, p, n)=\frac{1}{N}\left(\sum_{i=1}^{N} \max \left\{d\left(a_{i}, p_{i}\right)-d\left(a_{i}, n_{i}\right)+\operatorname{margin}, 0\right\}\right)\\
\text { where } d\left(x_{i}, y_{i}\right)=\left\|\mathbf{x}_{i}-\mathbf{y}_{i}\right\|_{2}^{2}\\
a\ \text{: anchor sample}\\
p\ \text{: positive sample}\\
n\ \text{: negative sample}\\
N\ \text{: minibatch size}
変換後の特徴ベクトル間のユークリッド距離を組み込んだ損失関数。
計算にはanchor, positve, negativeの3つのサンプルが必要となります。
anchorは基準となるサンプル、positiveはanchorと同じクラスに属する別のサンプル、negativeはanchorと違うクラスに属するサンプルです。
このように3つサンプルを取ってくる手法をTriplet samplingといいます。
損失関数を見るとanchorとpositiveのユークリッド距離(の2乗)が小さくなり、
anchorとnegativeの距離が大きくなるように学習することがわかります。

Triplet samplingでは1回のサンプリングにつき1つのpositiveと1つのnegativeの対しか
学習できないため、学習効率が悪いという欠点があります。
そのため効率よく学習するにはなるべく寄与の大きいサンプルを選ぶなどの工夫が必要となります。
また学習効率の悪さを改善するために考案されたN-pair samplingというものもあります。
Softmax Loss
Softmax Lossはクラス分類のタスクでよく用いられるものですが、metric learningの文脈でも使われるみたいです。
Softmax Lossをmetric learningの文脈で用いる場合は、図のように学習時は通常のクラス分類のように学習を行い、評価時には最後の識別レイヤの直前の出力(feature descriptor)を変換後の特徴ベクトルとして評価を行います。
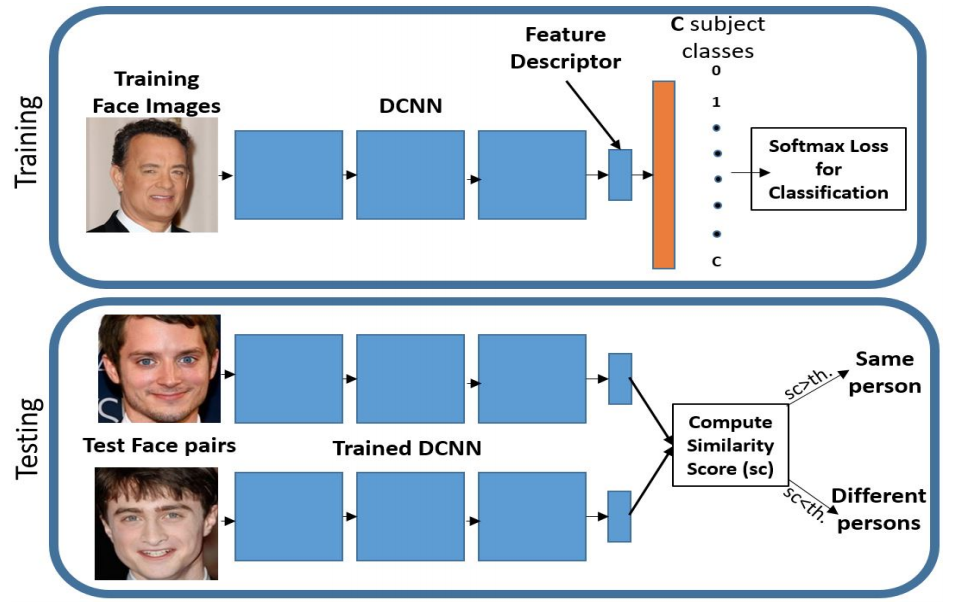
Softmax Lossを用いる場合1回の計算で1サンプルしか使わないため、Triplet Lossに比べて計算コストが小さくなります。しかしSoftmax Lossには次のような問題があります。
- 必ずしもデータ間の距離を最適化するとはかぎらない
- わかりやすい特徴にフィットしやすく、難しい特徴を無視する傾向がある
Softmax Lossを用いて学習を行うと真正面を向いている顔写真のようなわかりやすい画像では特徴ベクトルのL2ノルムが大きくなり、うつむいているわかりにくい画像ではL2ノルムが小さくなるという性質があるそうです。
そのため、わかりやすい画像の方に学習が引っ張られてしまい、難しい画像は無視される傾向があります。

これらの問題を克服したのがL2-constrained Softmax Lossです。
L2-constrained Softmax Loss
L2-constrained Softmax Loss(以後 L2 Softmax)には
- 同一クラスのコサイン類似度が大きく、違うクラスのコサイン類似度が小さくなるように学習する
- すべての特徴を均一に学習することができる
- 実装が簡単
といった特徴があります。
L2 Softmax Lossの式は次のとおりです。
\text{minimize } -\frac{1}{M} \sum_{i=1}^{M} \log \frac{e^{W_{y_{i}}^{T} f\left(\mathbf{x}_{i}\right)+b_{y_{i}}}}{\sum_{j=1}^{C} e^{W_{j}^{T} f\left(\mathbf{x}_{i}\right)+b_{j}}}\\
\text { subject to } \quad\left\|f\left(\mathbf{x}_{i}\right)\right\|_{2}=\alpha, \forall i=1,2, \dots M\\
L2 Softmax LossではSoftmax LossにFeature descriptorのL2ノルムがある定数$\alpha$になるように制約を加えます。これは入力データを半径$\alpha$の超球面上に埋め込んでいると解釈することができます。超球面状でSoftmax Lossをとることで、同一クラスの特徴ベクトル同士のコサイン類似度が大きくなり、違うクラスの特徴ベクトル同士のコサイン類似度が小さくなるように学習することができます。
論文ではSoftmax Lossで学習したモデルとL2-constrained Softmax Lossで学習したモデルを使ってMNISTデータを2次元の特徴ベクトルに変換してプロットしたものを比較しています。
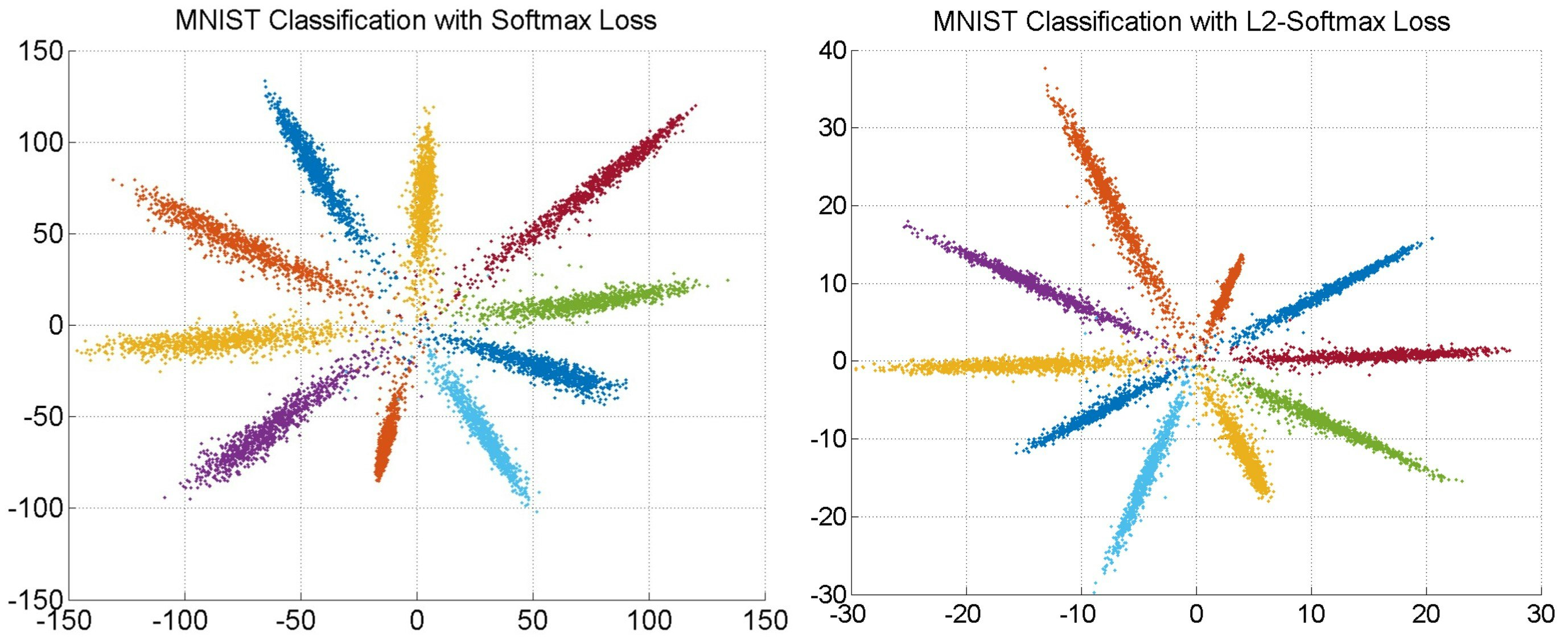
左の図がSoftmax Lossを用いて学習したもので右の図がL2 Softmaxを用いて学習したものです。
比較するとL2 Softmaxの方が角度に関するバラつきが小さくなっていることがわかります。
またFeture descriptorのL2ノルムを一定にすることによって全てのデータのLossへの影響が均一になります。そのため全ての特徴を均等に学ぶことができ、よりきわどいデータも学習することができます。
L2 Softmax LossはFeature descriptorの後に正規化を行うレイヤーと定数$\alpha$でスケーリングするスケーリングレイヤーをつけてSoftmax Lossを計算するだけで実現できるため非常に簡単に実装を行うことができます。

参考文献
[Rajeev Ranjan, Carlos D. Castillo, and Rama Chellappa. L2-constrained softmax loss for
discriminative face verification. CoRR, Vol. abs/1703.09507, , 2017.]
(https://arxiv.org/abs/1703.09507)
deep metric learningによるcross-domain画像検索