【Python/機械学習】なぜなにDeep Learning #1 パーセプトロン・ニューラルネットワーク

はじめに

機械学習エンジニアになるために、学習の記録を残す。コンスタントに書いていく。

今回は、ディープラーニングの基本となるパーセプトロンとニューラルネットワークを説明していく。

###注意
この記事は「ゼロから作るディープラーニング」(著:斎藤 康毅氏)を読みながら学習してきたメモである。
内容を鵜呑みせず、飽くまで参考程度に読んでいただきたい。(指摘・質問は大歓迎です。但し、優しい言葉に限る。)
リンク:ゼロから作るDeep Learning

目次

・パーセプトロンとは
・ニューラルネットワークとは

#この記事の

パーセプトロンとは

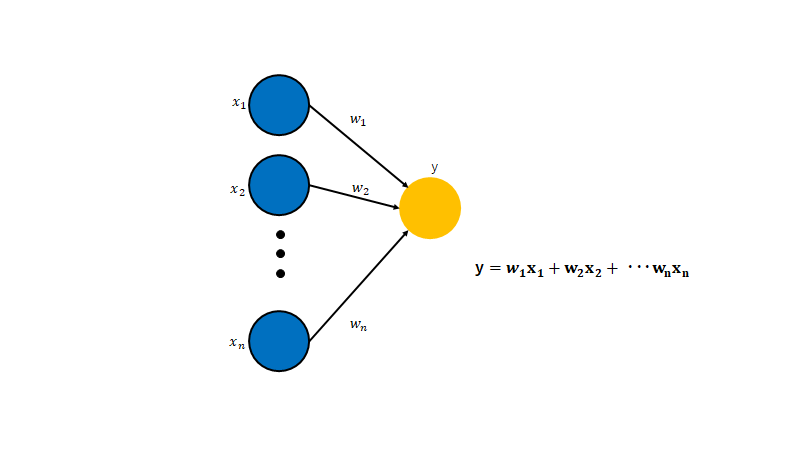
複数の入力に対して、一つの出力を返すアルゴリズムである。
論理回路のAND・OR・NANDのようなものだ。
ニューラルネットワークもといディープラーニングは、このアルゴリズムをベースに作られている。

# 入力数2のAND回路をパーセプトロンで書く
def AND(x1,x2,bias=0.5):
    tmp = w1*x1 +w2*x2 - bias
    if tmp <= 0:
        return 0
    elif tmp > 0:
        return 1   

出力に影響する変数は、入力値・重み・バイアスである。これらをパラメータと呼ぶ。
ニューラルネットワークは、パラメータを調整して学習させていく。

ニューラルネットワークとは

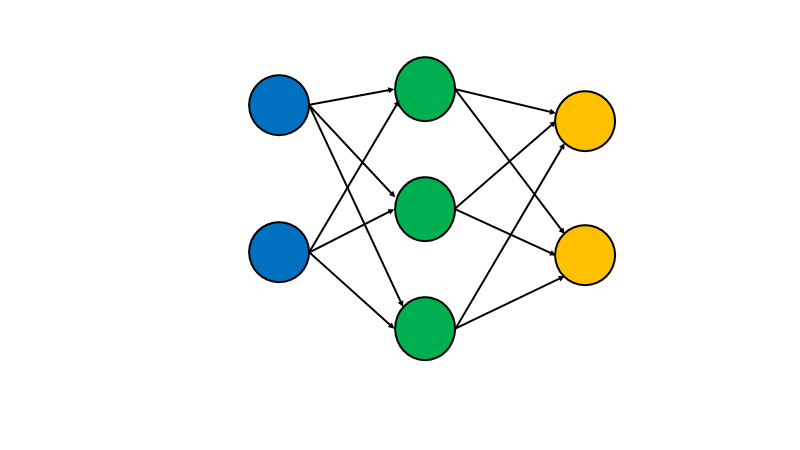
図を見てみると、多層パーセプトロンと変わらないように見える。
だが、パーセプトロンとの大きな違いがある。

####非線形の活性化関数を使うこと

###活性化関数とは？
入力信号(入力値・バイアス・重み)の総和が閾値を境に出力値が変わる。(発火する)
パーセプトロンも何も変わらない活性化関数を持っているというが、
ニューラルネットワークでは分類問題や回帰問題によって活性化関数の種類も変わる。

###なぜ活性化関数が必要なのか
活性化関数があることで、より多くの様々な値を出力できる。
入力値・重み・バイアスを調整するだけでなく、関数を変えることで出力値を変えられるようになる。

###非線形関数
分類問題・回帰問題だろうと、突き詰めると機械学習の目的は、精度をよくすることだ。
そのために、重みやバイアスを調整しながらパラメータを最適な値を見つける必要がある。
その微調整には、線形関数では解決できない。(少し値を変えるだけで大きく変わってしまうため)
非線形関数を利用することで、それを解決できる。