強化学習初心者です。強化学習はAI(人工知能)の中でも難解とされ、解説されているPythonのコードを見ても何をやってるのかわかりづらくて手こずりました。
ここではScratchで作った簡単なゲームでQ学習を直観的に理解することを目指します。Scratchを使うとキャラクター(スプライト)の動きや変数の変化からQ学習の仕組みが理解しやすいと思います。
Q学習(Q-Learning)の式
いきなり数式です。Q学習の説明でよく出てきます。(参考文献【2】4.4式より)
最初、この式が何を意味しているのかよくわかりませんでしたが、Scratchにこの式を組み込んでスプライトを動かしてみると直観的に理解できるようになると思います。
$$
q_\pi(s,a) \longrightarrow q_\pi(s,a) + \alpha \Bigl( r + \gamma q_\pi(s',\hat\pi(s')) - q_\pi(s,a) \Bigr)
$$
$s$ 状態
$s'$ 新しい状態
$a$ 行動
$q_\pi(s,a)$ 状態$s$において行動$a$をとったときのQ値
$\hat\pi(s')$ 新しい状態$s'$における最善(と思われる)行動
$q_\pi(s',\hat\pi(s'))$ 新しい状態$s'$に最善(と思われる)行動をとったときのQ値
$\alpha$ 学習率
$r$ 報酬
$\gamma$ 割引率
1次元グリッドのQ学習ゲームをやってみる
何はともあれ、とりあえずQ学習をゲームで体感してみましょう。
https://scratch.mit.edu/projects/488168812

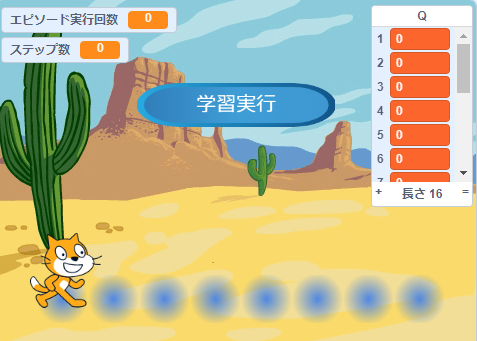
ネコ君が左端にいます。右端にダイヤが埋まっていますが、ネコ君は最初はそのことを知りません。
[学習実行]を押すと、ネコ君が動き回ってダイヤのある場所を偶然発見します。何回か動き回るうちにダイヤの埋まっている場所を覚えて迷わず進むようになります。
ダイヤを10回見つけると学習終了です。最後に[学習結果を披露]を押して、ネコ君が覚えた道を確認してみましょう。
ちなみにエピソードはダイヤをゲットすると1ずつ増え、ステップはネコ君が一歩進むたびに1ずつ増えます。
ここでのネコ君の動きを観察してみます。
1.最初は手がかりがないから、とにかく動き回るしかない
どこにダイヤが埋まっているのかわからない以上、調べまわるしかありません。ネコ君はそこらじゅうをウロウロします。
2.右端にダイヤが埋まっていると気づく
ウロウロしているうちに偶然ダイヤをゲットします(報酬$r$を獲得)。どうやらダイヤが右端の8番目のスポットに埋まっているようです。8番目のスポットにたどり着くには、7番目のスポットから一歩右に動けばいいことをネコ君が学習します。しかし残念ながら、(これまでウロウロしすぎたためか)どうやってこのスポットまで来たのかをネコ君はあまり覚えていないのです。
そのため、スタート位置からもう一度ダイヤを探そうとすると、7番目のスポットにたどり着くまで、またウロウロしないといけません。
3.ダイヤが埋まっているスポットまでの道筋を覚えだす
しかしネコ君は徐々に上達します。
7番目のスポットにたどり着くには、6番目のスポットから一歩右に進めばいい。
6番目のスポットにたどり着くには、5番目のスポットから一歩右に進めばいい。
・・・
という感じで道筋を覚えだし、あまりウロウロせずにダイヤが埋まっている場所までたどり着けるようになります。
4.一直線にダイヤの埋まっているスポットを目指すようになる
こうして8回ぐらい繰り返すと、ネコ君は左端から右端までの道筋を覚えて一直線にダイヤの埋まっている右端のスポットを目指せるようになります。
Q学習の仕組み
この一連のネコ君の行動から、Q学習がどのように進んでいるかを理解していきます。
※ここから先、このゲームに特化してかなり単純化して書いています。予めご了承ください。
Q値
Q学習ではQ値というものを利用します。
ダイヤが埋まっているスポットでは報酬 $r$ をゲットできるので、明らかに価値の高い場所です。そしてダイヤが埋まっているスポットに一番近いスポット(7番目)は、その次に価値の高い場所といえるでしょう。このスポットの価値をQ値というもので表すことにします。
q(s,a)
ただし、7番目のスポットにいることの価値が高いわけではなく、そこから一歩右に進む行動に価値があるわけですから、Q値はスポットの場所(このゲームの例では状態 $s$ にあたる)と、そのときにとる行動 $a$ でQ値を区別する必要があります。
そこで冒頭の数式のように $q(s_7,a_{7right})$ や $q(s_7,a_{7left})$ のようにQ値を表します。したがって各スポットには左へ行くときのQ値と右へ行くときのQ値と2つのQ値を持ちます。
※わかりやすいようにスポット番号と行動名を付記しました。
そして、ネコ君はより高いQ値を持つ方の行動をとることに決めます。
(行動の選択ルールを「行動ポリシー」と呼び、確率的な要素を持たずベストな行動をとり続ける行動ポリシーを「Greedyポリシー」と呼びます)
Q値の更新
ではQ値をどのように定めたらいいでしょうか。最初は何も情報がないので、Q値は全部ゼロにしておきます。
ネコ君がダイヤを発見したときには、7番目のスポットから一歩右に動いてたどり着いたときでした。したがってQ値 $q(s_7,a_{7right})$ に報酬 $r$ を加えて更新してあげることで、その行動の価値が高かったことをネコ君に教えてあげられそうです。
$$
q(s_7,a_{7right}) \longrightarrow r
$$
※便宜上、学習率 $\alpha$ や割引率 $\gamma$ は無視しました。
Q値の伝播
さらに7番目のスポットにたどり着くには、6番目のスポットから一歩右に動けばいいのでした。これについてもネコ君がこの行動をとったときに価値が高いことを教えてあげる(Q値を更新する)必要があります。
ただし、この行動をとってもダイヤをゲットできない(報酬はもらえない)ので、7番目のスポットが持っているQ値を使ってQ値を更新することにします。
$$
q(s_6,a_{6right}) \longrightarrow r + q(s_7,\hat\pi(s_{7}))
$$
※このゲームでは7番目のスポットの報酬 $r=0$ ですが、数式の都合上記載しておきます。
ここで$\hat\pi(s_{7})$は、7番目のスポットで最適(と考えられる)行動を表します。このゲームでは右に行くのが最適なのは明らかなので、$q(s_7,\hat\pi(s_{7}))$ は $q(s_7,a_{7right})$ と書いても差し支えないです。
先の式より $q(s_7,a_{7}) \longrightarrow r$ でしたので、結局 $q(s_6,a_{6}) \longrightarrow r$ となります。
以下、同様に計算していくと、報酬$r$がゴールからスタートに向かって伝播していき、最終的に1番目のスポットで右に一歩進む行動が $q(s_1,a_{1right}) \longrightarrow r$ となります。これがネコ君がダイヤが埋まっているスポットまでの道筋を覚えだす過程の動きの原理になっています。
ScratchでQ値の伝播を確認してみる
Scratchでは実行中の変数の変化を簡単に観察できるので試してみましょう。
リミックスして中身を確認してください。
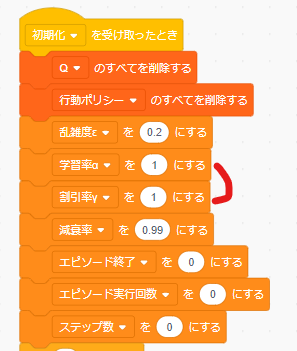
わかりやすくするため、背景のコードの初期化ブロックの中にある学習率 $\alpha$ と割引率 $\gamma$ の設定項目をともに1にしておきます。
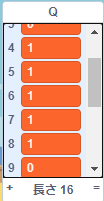
このリストQは次のように値を格納しています。したがって $q(s_7,a_{7right})$ はQの14番目になります。
- $q(s_1,a_{1left})$
- $q(s_1,a_{1right})$
- $q(s_2,a_{2left})$
- $q(s_2,a_{2right})$
- ・・・以降同様・・・
このゲームでは、ダイヤをゲットすると報酬 $r=+1$ がもらえることにしてあります。
ゲームを実行すると、最初にダイヤをゲットしたときに7番目のスポットにおいて右に一歩進む行動をとったときのQ値であるQの14番目が1になります。
$q(s_7,a_{7right}) = 1$
同様にして、次にネコ君が6番目から一歩右に動いて7番目のスポットにたどり着いたときは、Qの12番目 $q(s_6,a_{6right})$ が1になります。これを繰り返して、1番目のスポットまでQ値が伝播していきます。
上手くいかないこともある
残念ながらこの設定では、たまにネコ君が隣り合うスポットで右往左往を続けてしまいゴールにたどり着けないことがあります。
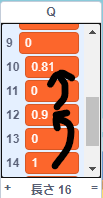
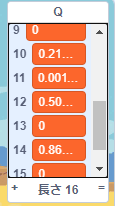
おそらく図のようにQの7番目$q(s_4,a_{4left})$と8番目 $q(s_4,a_{4right})$ がともに1になっているようなケースです。こうなると、ネコ君は左へ行けばいいのか右へ行けばいいのか判断できなくなってしまいます。
各種パラメータ
学習がちゃんと進むようにするため、いくつかパラメータをセットします。
割引率γ
先の例では報酬$r$が1番目のスポットまで伝播するようになっていました。これは1番目のスポットで右に行く行動のQ値 $q(s_1,a_{1right})$ と、ゴール直前の7番目のスポットで右に行く行動 $q(s_7,a_{7right})$ の価値が同じことを示しています。
しかし、ダイヤに近いスポットほど価値が高く、遠ざかるほど価値が低いと考えるのが自然ではないでしょうか。そこで設定するのが割引率 $\gamma$ です。0.9~0.99ぐらいに設定することが多いようです。
$$
q(s,a) \longrightarrow r + \gamma q(s',\hat\pi(s'))
$$
たとえば割引率 $\gamma=0.9$ を設定するとどうなるか見てみます。
\begin{align}
q(s_7,a_{7right}) &\longrightarrow& r &=& 1\\
q(s_6,a_{6right}) &\longrightarrow& r + \gamma q(s_7,\hat\pi(s_7)) &=& 0 + 0.9 \times 1 = 0.9\\
q(s_5,a_{5right}) &\longrightarrow& r + \gamma q(s_6,\hat\pi(s_6)) &=& 0 + 0.9 \times 0.9 = 0.81
\end{align}
このようにゴールから遠ざかるほどQ値を低くすることが出来ます。
ではScratchで試してみましょう。背景のコードで割引率 $\gamma$ を0.9にセットします。
実行すると、前のスポットになるほどQ値が割り引かれていく様子を確認できます。
乱雑度ε
ここまでの説明でQ学習の仕組みがざっくり理解できたかと思います。しかしネコ君の行動を見ていると不思議なことに気づくと思います。ネコ君の行動ポリシーは「Q値の高いほうの行動をとる」はずでした。このゲームでは常に右に進むのが正解ですが、学習が進んでも時々ネコ君が左に行ったり右往左往することもあります。
このようなランダム性を生み出すのが乱雑度 $\epsilon$ です。(ε‐グリーディ法)
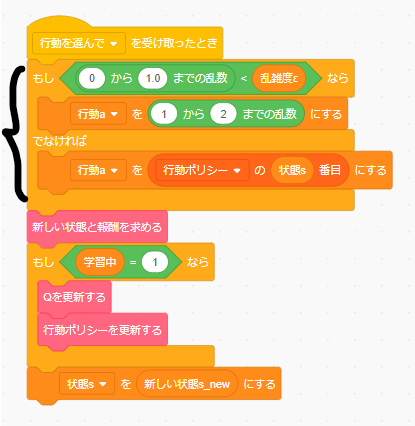
Scratchではネコのスプライトのコードの中で、以下のように表現されています。
例えば $\epsilon = 0.5$ とすると、 五分五分の確率で「行動をランダムに選択する」または「行動ポリシーに従う」ようになります。
今回のような簡単なゲームではあまり意味がないですが、複雑なゲームになってくるといったん選択した行動が絶対に正しいという保証がないため、周囲の環境を探索するような目的で使われます。ゲームの内容によって調整するといいと思います。通常は0.2とか0.3ぐらいの値を設定することが多いようです。
乱雑度εの減衰率
乱雑度 $\epsilon$ は周囲の環境を探索する目的がありましたが、学習が進んできて状況が見えてくると、あまり探索が必要なくなります。そこで、徐々に $\epsilon$ を下げる目的で減衰率を導入しています。
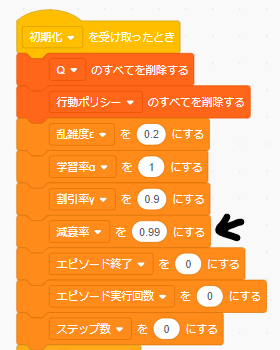
Scratchでは学習実行ボタンのスプライトのコードで、エピソードが1回終わるたびに乱雑度 $\epsilon$ に減衰率をかけて、徐々に下げています。

学習率α
実はこのゲームでは学習率 $\alpha$ がなくてもちゃんと学習できるのですが、複雑な問題に対応するため学習率 $\alpha$ を導入します。
ここまでのQ値の更新の仕方をおさらいすると、
$$
q(s,a) \longrightarrow r + \gamma q(s',\hat\pi(s'))
$$
となっており、元のQ値を無視して新しいQ値で置き換えるようになっていました。これは過去の経験をすべて捨てて、新しく得られた情報で上書きすることを意味します。
このゲームでは常に右に行くのが正解なので、この方法でも構わないのですが、複雑な問題になると過去の経験をすべて捨てるのは乱暴です。
そこで、新しく得られた情報を元に少しずつQ値を更新することにします。
まず、得られた報酬+新しいQ値と元のQ値の差分は次のようになります。
$$
r + \gamma q(s',\hat\pi(s')) - q(s,a)
$$
これに学習率 $\alpha$ をかけて、元のQ値に加えます。学習率 $\alpha$ は0.1~0.2ぐらいに設定することが多いようです。
$$
q(s,a) \longrightarrow q(s,a) + \alpha \Bigl( r + \gamma q(s',\hat\pi(s')) - q(s,a) \Bigr)
$$
このゲームではネコ君の行動にあまり変化は見られないと思いますが、Qの値を見ると更新による変化が緩やかになっていることがわかると思います。
数式の復習
冒頭の数式を再掲します。 $q(s,a)$ は行動ポリシー $\pi$ ごとに変わるものなので、ここでは $q_\pi(s,a)$ と添え字をつけています。
Scratchでパラメータを変化させてネコ君の行動を観察することで、各項の持つ意味が直観的に理解できたかと思います。
$$
q_\pi(s,a) \longrightarrow q_\pi(s,a) + \alpha \Bigl( r + \gamma q_\pi(s',\hat\pi(s')) - q_\pi(s,a) \Bigr)
$$
参考文献
【1】 ScratchでAIを学ぼう ゲームプログラミングで強化学習を体験
https://www.amazon.co.jp/dp/4296106945
【2】 ITエンジニアのための強化学習理論入門
https://www.amazon.co.jp/dp/4297115158