More than 3 years have passed since last update.

[CovsirPhy] COVID-19データ解析用Pythonパッケージ: S-R trend analysis

Last updated at 2020-12-24Posted at 2020-09-12

Introduction

COVID-19のデータ（PCR陽性者数など）のデータを簡単にダウンロードして解析できるPythonパッケージ CovsirPhyを作成しています。

紹介記事：

今回はS-R trend analysis（感染拡大状況のトレンドの分析法）のご紹介です。

英語版のドキュメントはCovsirPhy: COVID-19 analysis with phase-dependent SIRs, Kaggle: COVID-19 data with SIR modelをご参照ください。

1. 実行環境

CovsirPhyは下記方法でインストールできます！Python 3.7以上, もしくはGoogle Colaboratoryをご使用ください。

安定版：pip install covsirphy --upgrade
開発版：pip install "git+https://github.com/lisphilar/covid19-sir.git#egg=covsirphy"

import covsirphy as cs
cs.__version__
# '2.8.2'

	実行環境
OS	Windows Subsystem for Linux
Python	version 3.8.5

本記事の表及びグラフは2020/9/11時点のデータを使用して作成しました。実データをCOVID-19 Data Hub¹よりダウンロードするコード²はこちら：

data_loader = cs.DataLoader("input")
jhu_data = data_loader.jhu()
population_data = data_loader.population()

日本の感染者数ですが、厚生労働省HPの値³とは異なる値が出力されるようです。厚生労働省の値を使用したい場合は、次のコードによりCOVID-19 dataset in Japanからデータをダウンロードしてデータを置き換えてください。その際ImportError/ModuleNotFoundError: requests and aiohttpが発生した場合はpip install requests aiohttpによりインストールをお願いします（原因調査中、requestsは依存パッケージに含めているはずなんですが...）。

→ DataLoader.jhu()内で自動的にCOVID-19 dataset in Japanをダウンロードするようにしました。DataLoader.japan()の呼び出しは不要です。（2020/12/24追記）

v2.13.0以降不要

japan_data = data_loader.japan()
jhu_data.replace(japan_data)
# Citation -> str
print(japan_data.citation)

2. データの確認

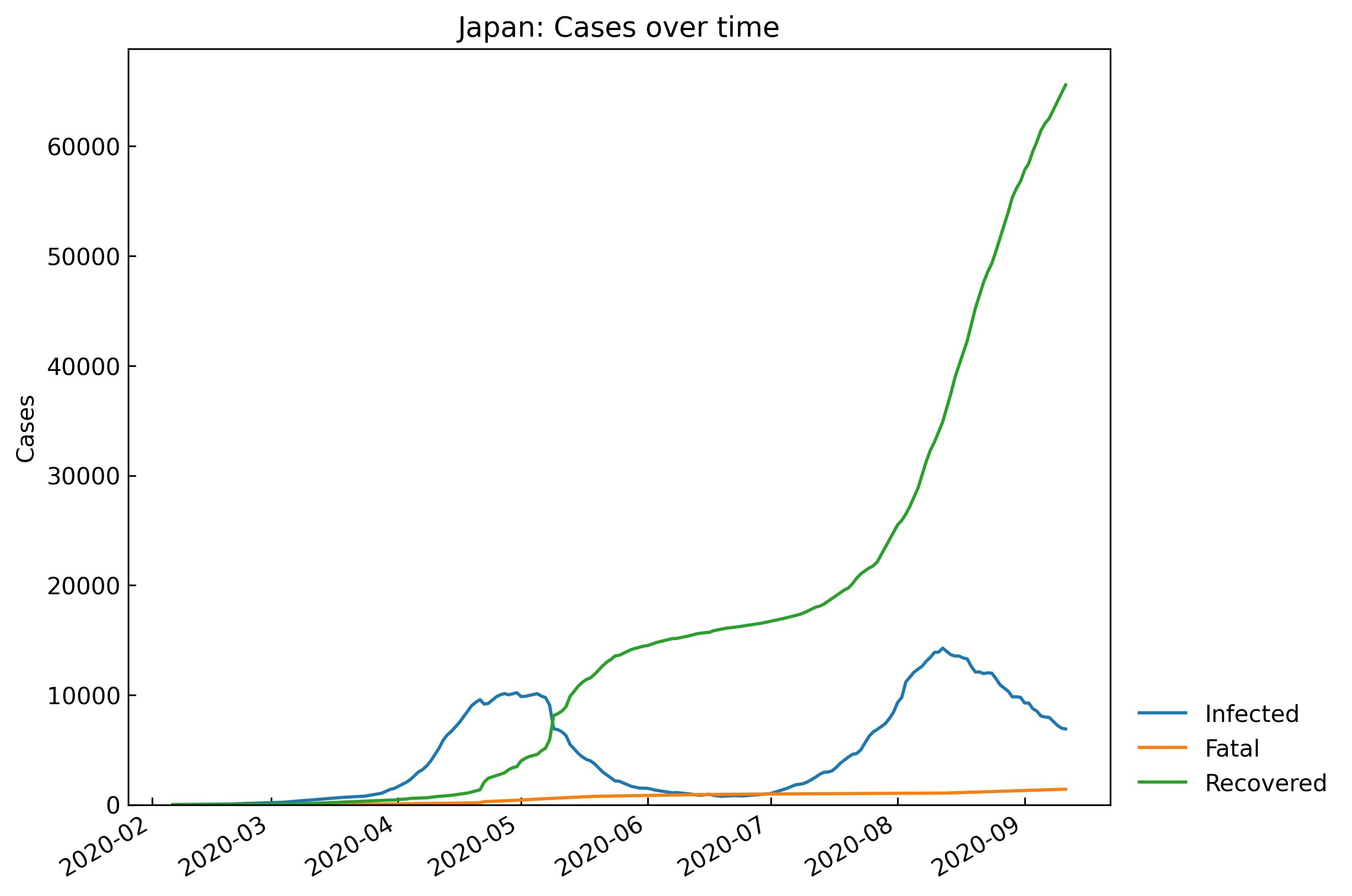
S-R trend analysisの説明に入る前に、Scenario.records()を使って実データ（例として日本のデータ）を眺めます。

snl = cs.Scenario(jhu_data, population_data, country="Japan")
# グラフを表示しない場合
snl.records(show_figure=False)

	Date	Confirmed	Infected	Fatal	Recovered
209	2020-09-07	71856	7957	1363	62536
210	2020-09-08	72234	7575	1377	63282
211	2020-09-09	72726	7233	1393	64100
212	2020-09-10	73221	6980	1406	64835
213	2020-09-11	73901	6899	1412	65590

# グラフを表示する
# filename: デフォルト値=None (画像ファイルとして保存しない)
_ = snl.records(filename=None)

3. S-R trend analysisの目的

SIR modelなど連立常微分方程式を使って感染症データを扱う場合、次のいずれかの前提の下で解析を行うことが一般的です。

モデルのパラメータは流行開始から終息まで一定
モデルのパラメータは毎日変動し、Poisson分布などに従う

しかしCOVID-19の解析を行う場合、どちらか一方を採用するのではなく、カスタマイズする必要があると考えました。

まず今回の流行では、感染が世界に拡大し始めた2020年2月, 3月ごろから各国や各個人が流行を抑えるための何らかの対策を執ってきました。感染率などパラメータは随時変動しており、終息まで一定と仮定することはできません（前述の実データ及びSIR-F modelの波形⁴より明らか）。

一方でパラメータが毎日変動するとなりますと、取得したデータの値ひとつひとつにかなり依存した解析になってしまいます。特に初期において検査体制が確立されていなかったこと、無症状でも感染力を持つ可能性があることから、COVID-19の場合は1日1日のデータではなく流行の概形を捉えることが必要と考えました。

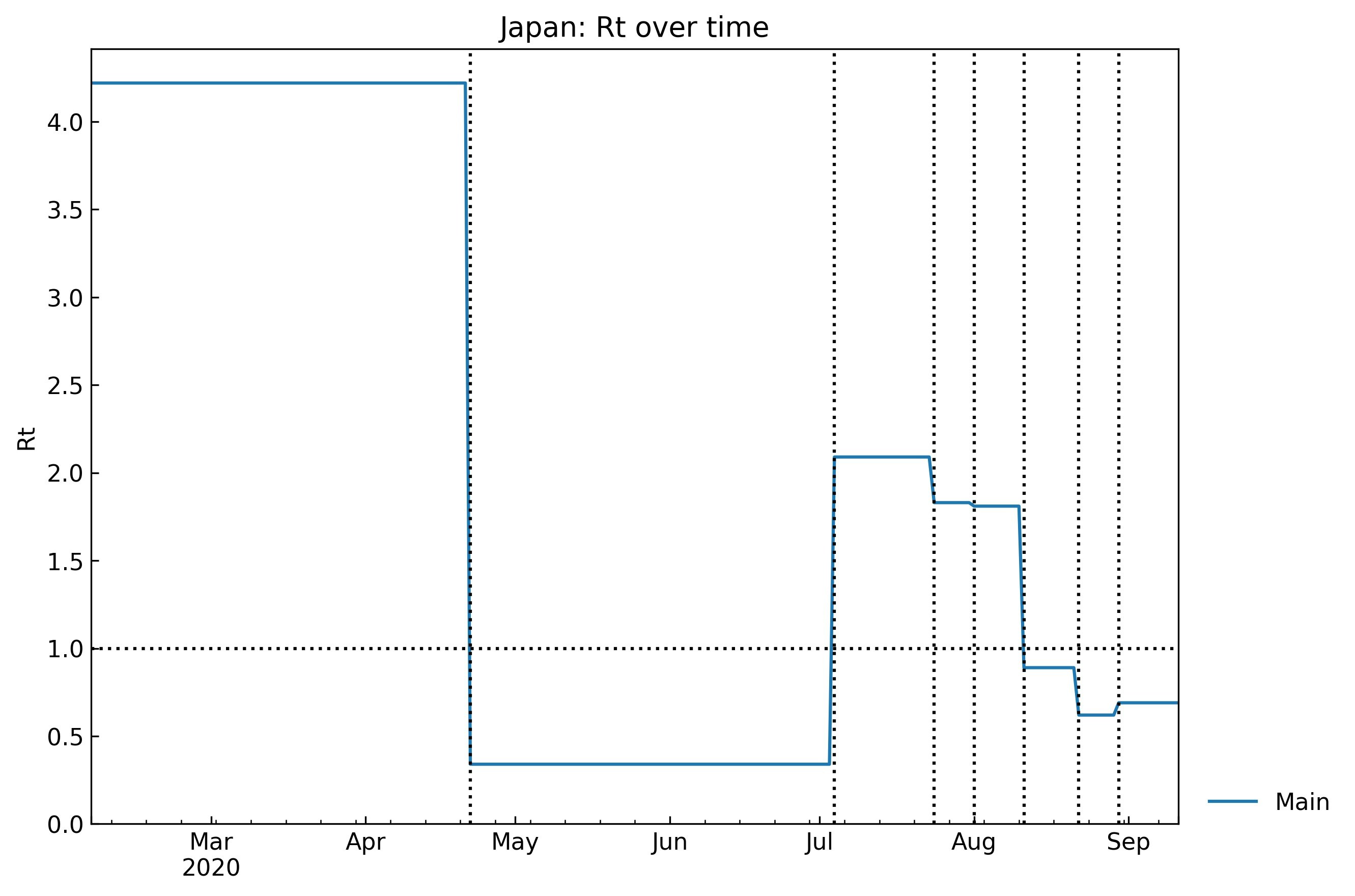
そこでCovsirPhyでは、パラメータが一定と思われる期間に細かく分割することで両者のいいとこ取りをしようと考えました。「パラメータが一定となる期間」を"Phase"と呼んでいます。流行開始から終息まで、パラメータの異なるPhaseが複数連なります。コードは別の記事に記載する予定ですが、たとえばSIR-F modelの実行再生産数$R_{\mathrm{t}}$はグラフのように階段状に変化すると考えます。

ではPhaseはどのようにして設定したら良いのでしょうか？パラメータの計算にはある程度時間がかかるため⁵、パラメータの計算を行わずにPhaseの分岐点（パラメータの値が変化する日付）を求めたいところです。

4. しくみ

S-R trend analysisを使用すると、感受性保持者数$S$と回復者数$R$の推移からPhaseの分岐点を求めることができます。思いつくまでの過程については長くなるので省略しますが、Kaggle: COVID-19 data with SIR model, S-R trend analysisに記載していますのでぜひご参照ください。

SIR model⁶, SIR-F model⁴の連立常微分方程式では、$S$, $R$に関して次のようになっています。

\begin{align*}
& \frac{\mathrm{d}S}{\mathrm{d}T}= - N^{-1}\beta S I  \\
& \frac{\mathrm{d}R}{\mathrm{d}T}= \gamma I  \\
\end{align*}

$\frac{\mathrm{d}S}{\mathrm{d}T}$を$\frac{\mathrm{d}R}{\mathrm{d}T}$で割ってみましょう。

\begin{align*}
\cfrac{\mathrm{d}S}{\mathrm{d}R} &= - \cfrac{\beta}{N \gamma} S  \\
\end{align*}

これを積分して$a=\frac{\beta}{N \gamma}$と置けば⁷、

S_{(R)} = N e^{-a R}

両辺を対数で割って、

\log S_{(R)} = - a R + \log N

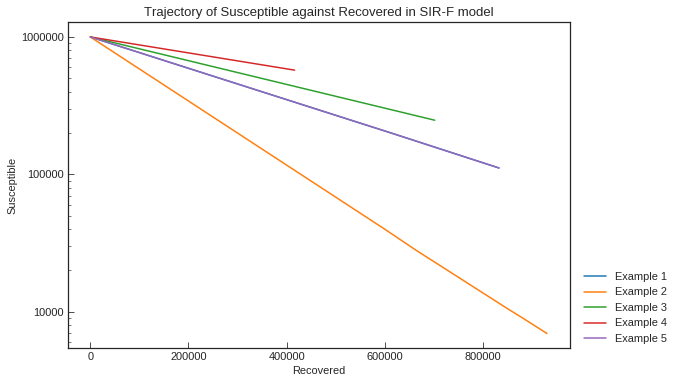
モデルのパラメータが一定のとき、x軸を回復者数$R$, y軸を感受性保持者数$S$として片対数グラフを描くと直線になる！

(グラフ：上述のKaggle Notebookより、パラメータを変えたときの直線の傾きの違い)

5. コード例

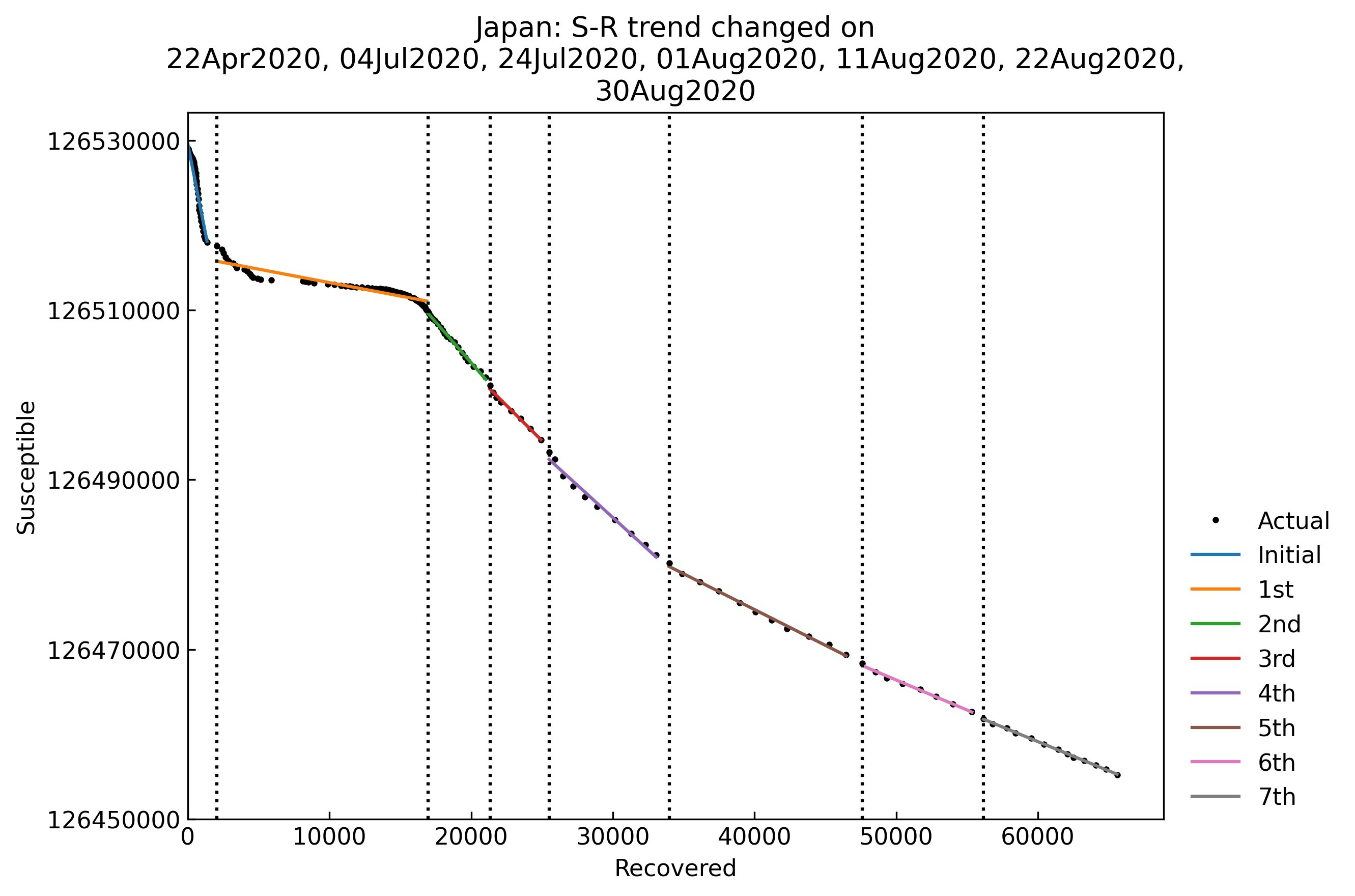
Scenario.trend()メソッドにより1行で実行できます。S-Rの片対数グラフが表示されます。PhaseはInitial (0th) phase, 1st phase, 2nd phase,...と名前をつけています⁸。

# show_figure: グラフを表示する
# filename: デフォルト値=None (画像ファイルとして保存しない)
snl.trend(show_figure=True, filename=None)

各Phaseの開始日と終了日の一覧はScenario.summary()メソッドによってデータフレーム形式で取得できます。

snl.summary()

	Type	Start	End	Population
0th	Past	06Feb2020	21Apr2020	126529100
1st	Past	22Apr2020	03Jul2020	126529100
2nd	Past	04Jul2020	23Jul2020	126529100
3rd	Past	24Jul2020	31Jul2020	126529100
4th	Past	01Aug2020	10Aug2020	126529100
5th	Past	11Aug2020	21Aug2020	126529100
6th	Past	22Aug2020	29Aug2020	126529100
7th	Past	30Aug2020	11Sep2020	126529100

総人口の値によって感受性保持者数$S$の値が変化してしまうため、重要な解析条件として一緒に表示するようにしています。また、本記事では出てきませんがパラメータの推測値などもScenario.summary()メソッドによって一覧表示できます。実データの登録されていないPhaseがある場合は、該当する行のType欄が"Future"となります。

今回は省略しますが、Scenario.add(), Scenario.combine(), Scenario.delete(), Scenario.separate(), Scenario.clear()によって上記Phase設定を編集することも可能です。

6. 実装

Phaseの分岐点の数を求めて分岐点となる回復者数を計算するため、rupturesパッケージを使用しています。時系列解析パッケージとして有名なfbprophetをもともと使用していましたが、分岐点の数を手動で設定しなければならないという問題がありました。ColaboratorのIlyass Tabialさんに教えていただき⁹、rupturesを使って分岐点の数も自動で推測できるようにしました。

covsirphy.ChangeFinderの実装コードより、主な手順は次の通りです。

各日付のS, Rの値を取得する
log10(S)を計算する
R=1, 2, 3..についてlog10(S)の値を設定する：データにない場合は前後の値から穴埋めする
計算量を抑えるためサンプリングする：サンプリング数 = 元データの個数
Rupturesパッケージにより、回復者数の変化量に対してlog10(S)が大きく変化する点の集合(R, log10(S))を求める
変化点の集合のlog10(S)を元データと照合し、各変化点の日付を求める（元データにない場合は近似値。Rより確定症例数のほうが変動は大きいためlog10(S)を使用した）
変化点の日付から各Phaseの開始日と終了日を計算する

あとがき

次回は各Phaseについてパラメータを推測する方法をご説明します。

お疲れさまでした！

Guidotti, E., Ardia, D., (2020), “COVID-19 Data Hub”, Journal of Open Source Software 5(51):2376, doi: 10.21105/joss.02376. ↩
[CovsirPhy] COVID-19データ解析用Pythonパッケージ: Data loading ↩
厚生労働省定義の「陽性者数」「退院又は療養解除となった者の数」「死亡者数」を確定症例数Confirmed, 回復者数Recovered, 死亡者数Fatalとして扱った場合。 ↩
[CovsirPhy] COVID-19データ解析用Pythonパッケージ: SIR-F model ↩ ↩²
10 phases, 8 CPUの並列計算で2分程度かかる。1ヶ国の分析であれば待てるが、データが毎日増えること、多数の国のデータを分析する場合があることを考えると時間がかかって大変。 ↩
[CovsirPhy] COVID-19データ解析用Pythonパッケージ: SIR model ↩
SIR modelにおいてS-R平面を解析した先駆者：Balkew, Teshome Mogessie, "The SIR Model When S(t) is a Multi-Exponential Function." (2010).Electronic Theses and Dissertations.Paper 1747. ↩
関連技術：[Python] 自然数を序数に変換する ↩
GitHub issue: How to predict the number of cases accurately #3 ↩

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up