Introduction
COVID-19のデータ(PCR陽性者数など)のデータを簡単にダウンロードして解析できるPythonパッケージ CovsirPhyを作成しています。パッケージを使用した解析例、作成にあたって得られた知識(Python, GitHub, Sphinx,...)に関する記事を今後公開する予定です。
英語版のドキュメントはCovsirPhy: COVID-19 analysis with phase-dependent SIRs, Kaggle: COVID-19 data with SIR modelにて公開しています。
**今回はSIR-F modelについてご紹介します。**実データは出てきません。
英語版:Usage (details: theoretical datasets)
1. 実行環境
CovsirPhyは下記方法でインストールできます!
Python 3.7以上, もしくはGoogle Colaboratoryをご使用ください。
- 安定版:
pip install covsirphy --upgrade - 開発版:
pip install "git+https://github.com/lisphilar/covid19-sir.git#egg=covsirphy"
# データ表示用
from pprint import pprint
# CovsirPhy
import covsirphy as cs
cs.__version__
# '2.8.2'
| 実行環境 | |
|---|---|
| OS | Windows Subsystem for Linux |
| Python | version 3.8.5 |
2. SIR-F modelとは
SIR-F modelは、広く知られた基本モデルSIR model1をもとに作成した派生モデルです。Kaggleのデータを用いて解析を進める中で作成しました2。
(新規性のあるモデルだと考えておりますが、2020年2月以前に公開された原著論文などご存知でしたら教示ください!筆者は感染症の専門家ではございません...)
SIR model
まずSIR modelでは、Susceptible(感受性保持者)がInfected(感染者)と接触したとき、感染する確率をEffective contact rate $\beta$ [1/min]と定義します。$\gamma$ [1/min]はInfectedからRecovered(回復者)に移行する確率です34。
\begin{align*}
\mathrm{S} \overset{\beta I}{\longrightarrow} \mathrm{I} \overset{\gamma}{\longrightarrow} \mathrm{R} \\
\end{align*}
SIR-D model
しかしSIR modelではFatal(死亡症例数)が考慮されいない、もしくはRecoveredの中に含まれてしまっています。COVID-19の場合は確定症例数(PCR陽性者数)、回復者数、死亡者数のデータがジョンズ・ホプキンス大学などによって収集5されており、モデルの変数としてそれぞれ使用することができます。なお確定症例数は感染者数$I$、回復者数$R$、死亡者数$D$の合計です。
SIR-D model:
$\alpha_2$ [1/min]を感染者の死亡率として、
\begin{align*}
\mathrm{S} \overset{\beta I}{\longrightarrow}\ & \mathrm{I} \overset{\gamma}{\longrightarrow} \mathrm{R} \\
& \mathrm{I} \overset{\alpha_2}{\longrightarrow} \mathrm{D} \\
\end{align*}
SIR-F model
さらにCOVID-19の場合は感染の確定診断が難しく、特に初期においては確定診断前に亡くなる症例が多数報告されました。こうした事例を反映させたモデルは次の通りです。$S^{\ast}$は確定診断がついた感染者、$\alpha_1$ [-]は$S^{\ast}$のうち確定診断の時点で亡くなっていた感染者の割合(単位なし)を示しています。
SIR-F model:
\begin{align*}
\mathrm{S} \overset{\beta I}{\longrightarrow} \mathrm{S}^\ast \overset{\alpha_1}{\longrightarrow}\ & \mathrm{F} \\
\mathrm{S}^\ast \overset{1 - \alpha_1}{\longrightarrow}\ & \mathrm{I} \overset{\gamma}{\longrightarrow} \mathrm{R} \\
& \mathrm{I} \overset{\alpha_2}{\longrightarrow} \mathrm{F} \\
\end{align*}
$\alpha_1=0$のとき、SIR-F modelはSIR-D modelに一致します。
3. 連立常微分方程式
総人口$N = S + I + R + F$として、
\begin{align*}
& \frac{\mathrm{d}S}{\mathrm{d}T}= - N^{-1}\beta S I \\
& \frac{\mathrm{d}I}{\mathrm{d}T}= N^{-1}(1 - \alpha_1) \beta S I - (\gamma + \alpha_2) I \\
& \frac{\mathrm{d}R}{\mathrm{d}T}= \gamma I \\
& \frac{\mathrm{d}F}{\mathrm{d}T}= N^{-1}\alpha_1 \beta S I + \alpha_2 I \\
\end{align*}
4. 無次元パラメータ
このまま扱っても良いですが、パラメータの範囲を$(0, 1)$に限定するため無次元化します。今回の記事では出てきませんが、実データからパラメータを計算する際に効果を発揮します。
$(S, I, R, F) = N \times (x, y, z, w)$, $(T, \alpha_1, \alpha_2, \beta, \gamma) = (\tau t, \theta, \tau^{-1}\kappa, \tau^{-1}\rho, \tau^{-1}\sigma)$, $1 \leq \tau \leq 1440$ [min]として、
\begin{align*}
& \frac{\mathrm{d}x}{\mathrm{d}t}= - \rho x y \\
& \frac{\mathrm{d}y}{\mathrm{d}t}= \rho (1-\theta) x y - (\sigma + \kappa) y \\
& \frac{\mathrm{d}z}{\mathrm{d}t}= \sigma y \\
& \frac{\mathrm{d}w}{\mathrm{d}t}= \rho \theta x y + \kappa y \\
\end{align*}
このとき、
\begin{align*}
& 0 \leq (x, y, z, w, \theta, \kappa, \rho, \sigma) \leq 1 \\
\end{align*}
5.(基本/実効)再生産数
SIR-F modelの(基本/実効)再生産数 Reproduction numberは、SIR modelの定義式6を拡張して次のように定義しました。
\begin{align*}
R_t = \rho (1 - \theta) (\sigma + \kappa)^{-1} = \beta (1 - \alpha_1) (\gamma + \alpha_2)^{-1}
\end{align*}
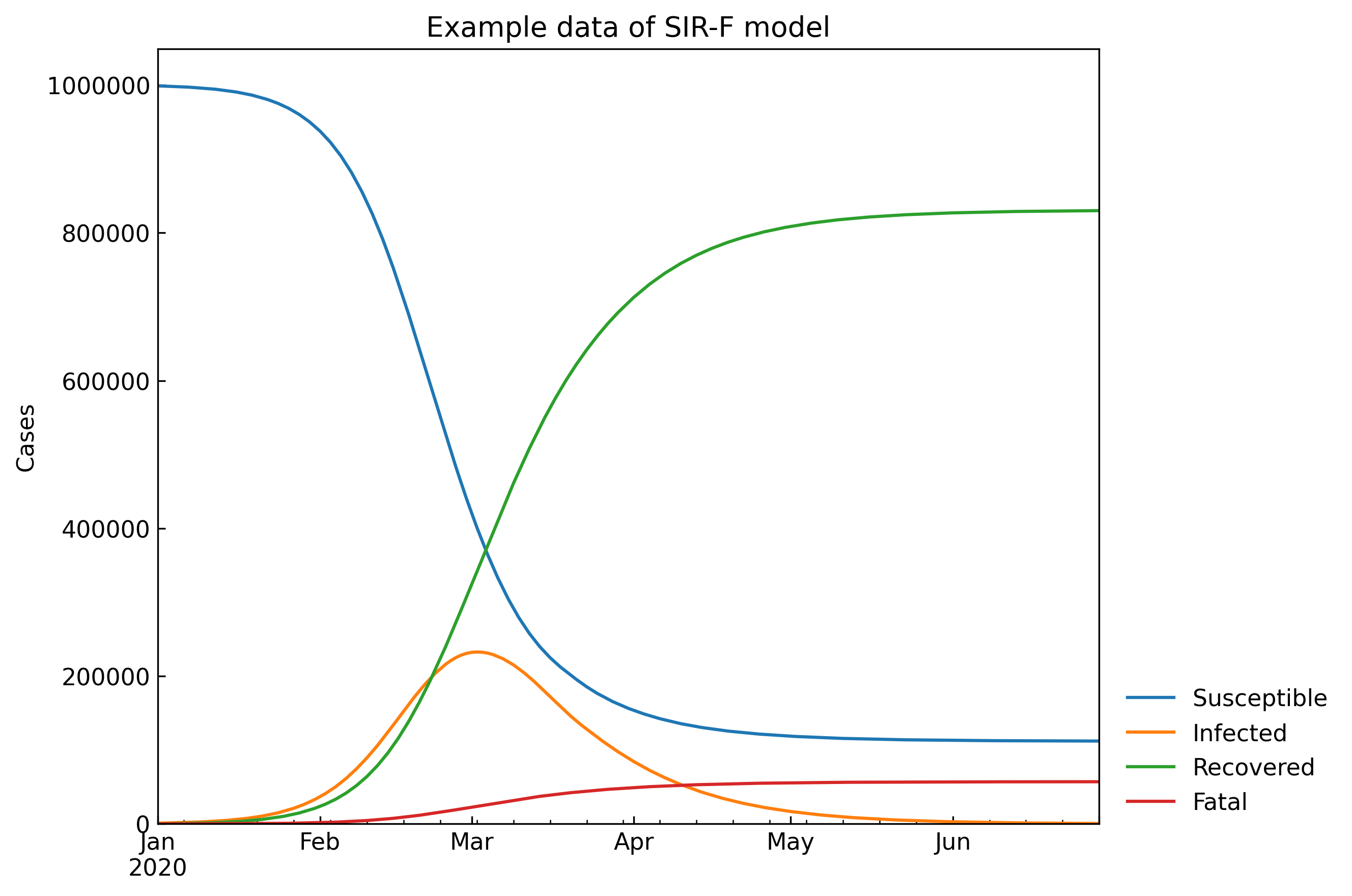
6. データ例
パラメータ$(\theta, \kappa, \rho, \sigma) = (0.002, 0.005, 0.2, 0.075)$及び初期値を設定してグラフ化します。
# Parameters
pprint(cs.SIRF.EXAMPLE, compact=True)
# {'param_dict': {'kappa': 0.005, 'rho': 0.2, 'sigma': 0.075, 'theta': 0.002},
# 'population': 1000000,
# 'step_n': 180,
# 'y0_dict': {'Fatal': 0,
# 'Infected': 1000,
# 'Recovered': 0,
# 'Susceptible': 999000}}
(基本/実効)再生産数:
# Reproduction number
eg_dict = cs.SIRF.EXAMPLE.copy()
model_ins = cs.SIRF(
population=eg_dict["population"],
**eg_dict["param_dict"]
)
model_ins.calc_r0()
# 2.5
グラフ表示:
# Set tau value and start date of records
example_data = cs.ExampleData(tau=1440, start_date="01Jan2020")
# Add records with SIR-F model
model = cs.SIRF
area = {"country": "Full", "province": model.NAME}
example_data.add(model, **area)
# Change parameter values if needed
# example_data.add(model, param_dict={"kappa": 0.001, "kappa": 0.002, "rho": 0.4, "sigma": 0.0150}, **area)
# Records with model variables
df = example_data.specialized(model, **area)
# Plotting
cs.line_plot(
df.set_index("Date"),
title=f"Example data of {model.NAME} model",
y_integer=True,
filename="sirf.png"
)
7. 次回
次回は実データをダウンロードして確認する手順をご説明します。