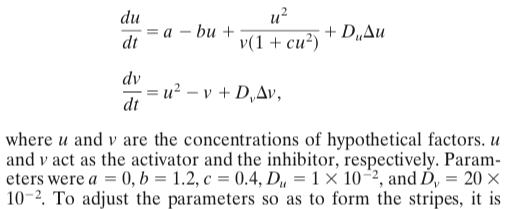はじめに
目的
- 反応拡散系を理解する
- 前回 確立した GPU の計算手法をさっそく適用してみる
この論文の再現を試みる。
特記なければ、引用はすべてこの論文から。
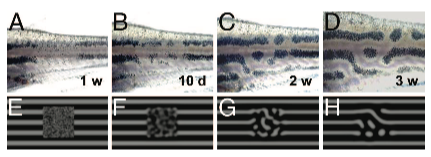
Pattern regulation in the stripe of zebrafish suggests an underlying dynamic and autonomous mechanism.
Yamaguchi M, Yoshimoto E, Kondo S.
Proc Natl Acad Sci U S A. 2007 Mar 20;104(12):4790-3. Epub 2007 Mar 12.
参考サイト
反応拡散系について
Mechanism of pigment pattern formation
反応拡散波とは
反応拡散系の実装例
チューリング波（反応拡散波）を理解したい
2次元Turingパターンの生成
反応系の代表例、反応拡散系の導入として
FitzHugh-南雲モデルで遊んでみる
論文の説明・補足
上の図は、ゼブラフィッシュにレーザーを当てて色素を消失させた部分に、注入した色素をもとに模様が再生する様子（上段）とそのコンピュータシミュレーション（下段）である。
シミュレーションは上の式に従ってやる。
ちなみに $\Delta u, \Delta v$ はラプラシアンで、時間の増分 $\Delta t$ と混同しないように。
論文中にセルサイズ $h$ が書かれていなくて引っかかったが、 $h = 0.05$ でうまくいった。 $h$ がこれより大きいと、縞が２つに分裂してしまう。
$h$ は拡散に関わっており、 $D_u / h^2 = 4, D_v / h^2 = 80$ の値が重要である。
$1/h^2$ はラプラシアン（＝２階微分）の操作で出てくる。
時間差分は $\Delta t = 0.001$ とした。
$4 \Delta t , D_v / h^2 = 0.32 < 0.5$ で拡散の差分法の安定条件はぎりぎり満たしている。
一方、 $\Delta t , D_u / h^2 = 0.004$ で、１０進法７桁精度の Float32 でも桁落ちまでは心配しなくてよさそうである。$u \sim 1,, h^2\Delta u \sim 0.1$ のとき $u+ \Delta t , D_u \Delta u$ の精度が２から３桁になってしまうが仕方がないだろう。
結果
Julia Notebook
https://gist.github.com/Lirimy/4d39643abccc519e21c77d261c0b6079
初期状態
経過（GIF アニメ）
さらに２倍ぐらい時間が経った状態
論文 (256x128) より大きな領域 (256x256) でシミュレーションしたのだが、たぶんうまくいっていると思う。
GIF アニメの計算と画像出力 85 秒
GPU 使用率 30% ぐらい
それでも CPU （実装としては結構遅いと思うが）と比べると 50 倍以上速い。
ありがたいのは、CPU の（ベクトル的な）実装からほとんど変更なしに GPU で動かせること。
CPU でパフォーマンスを気にするよりも、何も考えずに GPU に載せたほうが良い。
と思っていたが、実は精度の検討は結果をまとめたあと、記事を書きながら行っていて、意外とシビアなバランスの上で成り立っていたということに気づいて震撼している。