はじめに
コード/Jupyter Notebook
https://gist.github.com/Lirimy/5ad7e50c4fae1ed0700629cf4877ad7e
動機
テーマについて
「質的な違い」というものがどうして生まれるのかを知りたい。その一つのアプローチとして取り組む。
分岐は何らかの制御パラメータ (control parameter) の変化によって生じる転移や不安定化についてのモデルを与えている[ストロガッツ p.50]
ストロガッツの補完として
[ストロガッツ]は,分岐現象の定番ともいえる教科書だが,日本語版の底本となっている原著第1版は1994年1の出版である。当時は,現在ほどにはプログラミングが手軽にできる環境ではなかったであろうため,どうしても数値計算方面の記述が薄く,一部の限られた計算が例題として載せられているのみである。
そこで,ストロガッツを現在の状況に合わせてアップデートしたらどうなるだろうか,という個人的な試みとしてこの記事を位置付けたい。数値計算という強力なツールを用いて,できるだけ本筋の議論を追っていきたい。
個人的な技術面での理由
- 解析的に解けないモデルにも適用できるような,分岐解析の数値計算手法を確立したい
- Julia の数値計算ライブラリの使い方に慣れたい
計算環境
julia> versioninfo()
Julia Version 1.1.0
Commit 80516ca202 (2019-01-21 21:24 UTC)
Platform Info:
OS: Windows (x86_64-w64-mingw32)
CPU: Intel(R) Core(TM) i5-2500K CPU @ 3.30GHz
WORD_SIZE: 64
LIBM: libopenlibm
LLVM: libLLVM-6.0.1 (ORCJIT, sandybridge)
この記事で利用するパッケージ
この記事では,数値計算の詳細には立ち入らず,既存のライブラリを積極的に利用していく。
結果を再現するためには,数値計算などのパッケージのインストールが必要である。
- NLsolve (非線形ソルバーで固定点を求める)
- ForwardDiff (自動微分で固定点のヤコビアンを求める)
- LinearAlgebra (安定性判別のため,ヤコビアンの固有値を求める)
- Plots (計算結果のグラフを描く)
julia> ]add NLsolve
双安定スイッチモデル
[ガードナー]より,ピッチフォーク分岐する双安定スイッチモデルを採用する。
互いに抑制し合う遺伝子から成る人工遺伝子回路[柚木]
\begin{eqnarray}
\begin{cases}
\dot{x} &=& \dfrac{a}{1+y^2} - x \\
\dot{y} &=& \dfrac{a}{1+x^2} - y
\end{cases}
\end{eqnarray}
$a$ は抑制因子の実効合成速度 (the effective rate of synthesis of repressor) 。
分類としては,連立非線形常微分方程式にあたる。
汎用的に利用できる手法を目指して,多変数からなるモデルを選択した。
モデルの解析解
この記事では,解析的には解けないモデルでも計算できるような手法の確立を目指しているが,計算がうまくいっているかの確認として解析解を求めてみる。
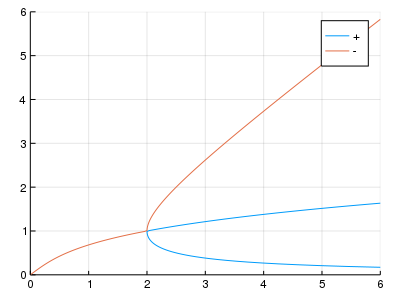
$ \dot{x} = \dot{y} = 0 $ より求められる次式2をプロットする。
a = \frac{(1+y^2)^2}{2y} \left( 1 \pm \sqrt{1-\frac{4y^2}{(1+y^2)^2}} \right)
$a$ が横軸,$y$ が縦軸。
次節では解析的な手法に頼らず,数値計算によってこのグラフの再現を試みる。
パラメータに応じた固定点を求める
$a$ を決めて,$\dot{x}=\dot{y}=0$ を満たす $(x, y)$ を求める。
ソルバーに渡す関数をつくる
関数では,あらかじめ確保しておいた配列に計算結果 (du) を保存するようにしておく。
最終行の nothing で,関数が戻り値を返さないようにしているが,必ずしもそうしなければならないわけでもない。
a = Ref{Float64}(2.)
function f!(du, u)
x, y = u
du[1] = a[] / (1 + y^2) - x
du[2] = a[] / (1 + x^2) - y
nothing
end
a[] = 3.
u = [1., 4.]
du = similar(u)
f!(du, u)
println(du) # [-0.823529, -2.5]
関数にパラメータを持たせるには?
パラメータ $a$ を Julia でどうやって実現すればよいかを検討する。
- パラメータは後から変更したい(関数の外から)
- ソルバーを使う関係上,引数には含められない
という制約がある。まず思いつくのは,単純にグローバル変数 a として関数内から参照することだが, @time のマクロで不具合が出た。おそらく変数のスコープの問題だと考えらえるが,深く追求していない。
そこで今回利用したのが RefPointer である。とりあえずの理解としては,C言語のポインターや一要素のみの配列のようなものかと受け取った。もちろん細かいところで違いはあるだろう。
a = Ref{Float64}(2.) # 初期値
println(a[]) # 2.0
a[] = 3. # 値の変更
println(a[]) # 3.0
コード量が多くなるため今回は採用しなかったが,他の手段としては,
- 配列や構造体を用いる
- Closure
- Function-like object
が挙げられる。
mutable struct BistableSwitch{T}
a::T
end
function (self::BistableSwitch)(du, u)
a = self.a
x, y = u
du[1] = a / (1 + y^2) - x
du[2] = a / (1 + x^2) - y
nothing
end
f! = BistableSwitch(2.0)
f!.a = 3.0 # パラメータの変更
参考:Julia で Closure のパフォーマンスを気にしてみる
NLsolve で固定点を求める
固定点とは,時間変化しない状態のことで,$ \dot{x} = \dot{y} = 0 $ を満たす。
パッケージ NLsolve で非線形方程式の解を数値的に求める。
using NLsolve
a[] = 3.
u0 = [1., 4.] # 初期値
r = nlsolve(f!, u0, autodiff=:forward)
Results of Nonlinear Solver Algorithm
* Algorithm: Trust-region with dogleg and autoscaling
* Starting Point: [1.0, 4.0]
* Zero: [0.381966, 2.61803]
* Inf-norm of residuals: 0.000000
* Iterations: 5
* Convergence: true
* |x - x'| < 0.0e+00: false
* |f(x)| < 1.0e-08: true
* Function Calls (f): 6
* Jacobian Calls (df/dx): 6
収束したかどうかは r.f_converged で,ゼロ点(固定点)は r.zero でアクセスできる。
du = zeros(2)
f!(du, r.zero)
println(du) # [1.66533e-16, -4.44089e-16]
パラメータを変化させて分岐図を描く
分岐図とは,パラメータ(ここでは $a$)に対応する固定点を図示したものである。
分岐図を描く際に注意しなければならないことがある。パラメータに対して固定点が複数存在しうるのだ。今回のモデルでいえば, $ a>2 $ のとき固定点が3つある。
パラメータに対する複数の固定点を漏らさず求めるには,初期値 $(x_0, y_0)$ の取り方が重要である。数値的に解を求める場合,初期値によって異なる解に行き着くためだ。今回は初期値を適当な範囲でランダムにとった。
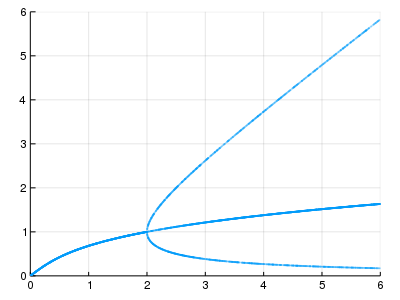
10000 個の固定点を求め,$(a, y)$ をプロットした。
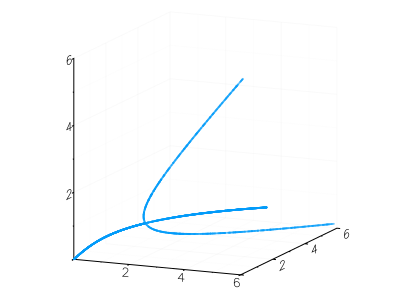
わざわざ2変数のモデルを選んだので,$(a, x, y)$ を3次元プロットしてみた。
それぞれの固定点の安定性を判別する
どうやるか?
固定点におけるヤコビアンを求め,固有値がすべて負であれば安定である。
詳しくは[ストロガッツ pp.165-167]や[柚木]を見てほしい。
ヤコビアンとは多変数における微分のようなものである。数値的に求める方法はいくつかあるが,ここでは自動微分のパッケージ ForwardDiff を用いることにする。
固有値は LinearAlgebra.eigvals で求める。
ForwardDiff で安定性を求める
using ForwardDiff
using LinearAlgebra
negative(x) = x < 0
stable(J) = reduce(&, negative.(eigvals(J)))
a[] = 4.
@show r = nlsolve(f!, [3., 3.], autodiff=:forward)
@show J = ForwardDiff.jacobian(f!, similar(r.zero), r.zero)
@show eigvals(J)
@show stable(J)
r = nlsolve(f!, [3.0, 3.0], autodiff=:forward) = Results of Nonlinear Solver Algorithm
* Algorithm: Trust-region with dogleg and autoscaling
* Starting Point: [3.0, 3.0]
* Zero: [1.3788, 1.3788]
* Inf-norm of residuals: 0.000000
* Iterations: 5
* Convergence: true
* |x - x'| < 0.0e+00: false
* |f(x)| < 1.0e-08: true
* Function Calls (f): 6
* Jacobian Calls (df/dx): 6
J = ForwardDiff.jacobian(f!, similar(r.zero), r.zero) = [-1.0 -1.3106; -1.3106 -1.0]
eigvals(J) = [0.310602, -2.3106]
stable(J) = false
安定性を含めて分岐図を描く
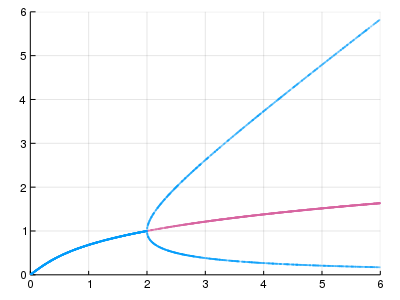
先ほど求めた分岐図を,安定性で色分けする。
青が安定,赤が不安定。
$a=2$ のところで3分岐し,真ん中の枝が不安定になるという,よく見る感じの3超臨界ピッチフォーク分岐の図が得られた。
参考文献
ストロガッツ
Steven H. Strogatz (1994) Nonlinear dynamics and chaos (Perseus Books)
[田中久陽他 訳, 非線形ダイナミクスとカオス (丸善出版, 2015)]
ガードナー
Gardner, T.S., Cantor, C.R. and Collins, J.J., Construction of a genetic toggle
switch in Escherichia coli., Nature 403(6767):339-42, 2000.
柚木
Primers for Mathematical Methods in Systems Biology
Chapter 2 Bifurcation Analysis
http://kurodalab.bs.s.u-tokyo.ac.jp/member/Yugi/Textbook/chapter2.pdf