これは「データ構造とアルゴリズム Advent Calendar 2018」14日目の記事です.
この記事は, Gabowの論文をもとに書かせていただいています. こっちを読むと完全に理解できます.
マッチング?
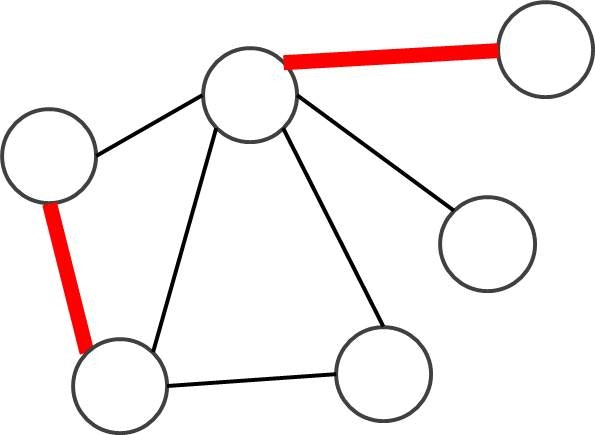
けんちょんさんの記事から画像をお借りしました.
マッチングは辺の集合であって, どの2辺も両端を共有しないようなものをマッチングといいます.
その集合の中で, 一番辺の数が多いものを最大マッチングといいいます.
二部マッチング?
二部グラフ(グラフの頂点が2グループに分かれていて, グラフの辺がその2グループをまたぐものしか無いグラフ)での二部マッチングは最大フローに帰着して解くことが出来ます.
導入
二部マッチングの問題は最大フローで解けたりしますが, 一般マッチングはそうはいきません.
また実装が難しいこと(Edmonds' Blossom Decomposition O(V^3) , 「組合せ最適化-理論とアルゴリズム」に書かれています)や, 競技プログラミングではAtCoderのrng_58さんが一般マッチングは出さないと発言したらしい(https://twitter.com/drken1215/status/1038437622840872962 , AtCoderの解説放送)ので競プロerには縁のない問題かも知れませんが, 見てくれたらありがたいです.
ここでは, このアルゴリズムの流れと実装を紹介しようと思います.
マッチングに関する基本的な理論
注意) **ここから先, Algorithmの実装の関係上, グラフの頂点は1-indexedです. **よろしくお願いします
二部マッチング, 一般マッチングに関して成り立つ一つの有名で重要な定理があるので紹介します.
Bergeの定理
グラフGのマッチングの辺の集合をMとおく.
このとき, GがM-増加パスを持っているならば, Mは最大マッチングではない.
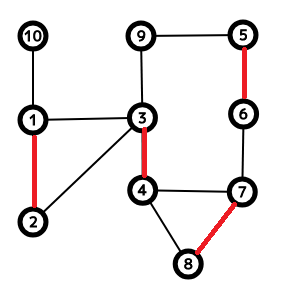
例を示しながら解説します. 以下のグラフを考えます.
赤い辺はマッチングの辺(Mに属する辺)です. このとき, 頂点1, 2, 3, 4, 5, 6, 7, 8はマッチングされていると言います
パスとは「2回以上同じ頂点を訪れていない道のり」のことです.
また, M-交互パスというものが存在します. これは「マッチングに使われている辺」と「使われていない辺」を交互に使ったパスです. 例えば1, 2, 3, 4, 8や9, 5, 6, 7, 8, 4があります.
M-増加パスはM-交互パスの両端がマッチングされていない頂点であるパスです.
なぜ増加というのでしょう?実は, M-増加パスに沿って次の操作(augmenting)を行うとわかります.
M-増加パスの辺のマッチングしている,していないの状態を入れ替える.
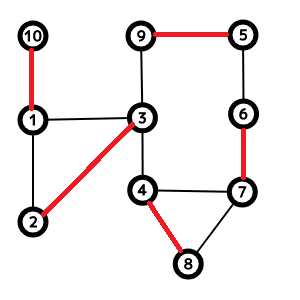
上のグラフのM-増加パスは10, 1, 2, 3, 4, 8, 7, 4, 3, 9です. これをaugmentingすると以下のようになります.
よく見ると, マッチングの辺数が増えていることがわかります.
また, このBergeの定理は逆も言えて, M-増加パスが存在しなければ, 最大マッチングである. なので,
M-増加パスが見つからなければアルゴリズムは最大マッチングを与えて終了します.
E Algorithm
それでは, Gabowが示したアルゴリズムの概要を書いていきます.
非自明な操作がたくさんありますが, 証明はまだ読めていないので割愛させていただきます.すみません.
ほとんどのマッチングアルゴリズムをものすごく大まかに表現すると以下のようになります.
- 何もマッチングしていない状態からスタート
- M-増加パスを見つけてそのパスに沿って増加する
- M-増加パスが見つからなければ終了する
E Algorithm の「M-増加パスを見つける」過程
E Algorithmは次のようにしてM-増加パスを見つけます.
- まだ始点に選んでいない頂点の中で, マッチングされていない頂点uを選びます.
- uをパスの端とするM-交互パスを見つけていきます. (実際にはBFSで辿ります)
このときvからuのM-交互パスであり, 最初の辺がマッチングの辺であるとき, vをouterと呼びます.
vがouterのときに, このvからuのM-交互パスを**P(v)**と書くことにします. - この操作の過程でマッチングされていない頂点u'( ≠ u)であり,
outerな頂点vとつなぐ辺(u', v)が存在するようなu'を見つけたとします.
このとき, パスu' -> P(v)はM-増加パスなので, 増加して1.に戻ります - M-増加パスが見つからなければ, また
1.に戻ります
P(v)の構成
ただ, 一つ一つの頂点に対してP(v)を持つのは計算量が悪すぎます.そこでGabowは3つの配列を用意しました(天才)
- mate[v] ... vとマッチングしている頂点を持ちます.
mate[v] == 0のときはマッチングしていません. - label[v] ... outerな頂点vに対してつけられる値です. P(v)を構成するに使います.
start label , vertex label , edge label , nonouter label の4種類があります. - first[v] ... P(v)上で一番最初の
nonouterな頂点を持ちます.
label[v]
start label
E Algorithmの探索の最初に選ぶ, マッチングされていない頂点uにつけられるlabelです.
実装ではlabel[u] = 0をstart labelとしています.
vertex label
outerな頂点vがvertex labelを持っているときは, label[v]はvとは異なる頂点を指します. 実装では1~Vの数が当てられます.
P(v)はv -> mate[v] -> P(label[v])というパスになります.
edge label
outerな頂点がedge labelを持っているときは, label[v]は辺の番号を持ちます. ここでは各辺(x, y)に対して番号付けした値num(xy)をつかってlabel[v] = num(xy)とします. 実装ではnum(xy)はV + 1以降の番号を使います.
P(v)はP(x)とP(y)から構成されます. P(x), P(y)のどちらかにvは含まれている(らしいです. 証明をまだ読めていないのでここでは割愛します. )ので,
含まれているパスをP(x)とします.
P(x)の一部分にxからvのパスがあります. これをP(v , x)と表現することにします.
すると, P(v)はrev P(v , x) -> P(y)というパスになります
nonouter label
outerでは無い頂点につけられます. 実装では負の値を使います.
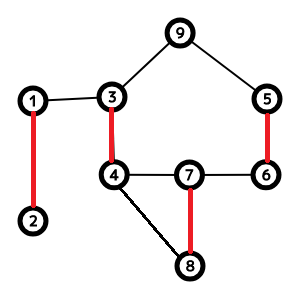
例
このままではよくわからないので例を見ながら説明します.
| No | kind | Label |
|---|---|---|
| 1 | nonouter | - |
| 2 | vertex | 3 |
| 3 | edge | num(6, 7) |
| 4 | vertex | 9 |
| 5 | edge | num(6, 7) |
| 6 | vertex | 9 |
| 7 | edge | num(4, 8) |
| 8 | vertex | 4 |
| 9 | start | - |
このような状態であるとします.
vertex label
頂点8に注目しましょう. 頂点8にはvertex labelが貼ってあります.なので,
P(v) = v -> mate(v) -> P(label[v])より
頂点8は頂点7とマッチングされているのでmate[v] = 7.
label[8] = 4
P(8) = 8 -> 7 -> P(4) です. またP(4)も頂点8と同じようにP(4) = 4 -> 3 -> 9 と決められるので,
P(8) = 8 -> 7 -> 4 -> 3 -> 9となります. グラフで確認するともちろんM-交互パスになっています.
edge label
7に注目してみましょう. 頂点7にはnum(4, 8)のedge labelが貼ってあります.
まずは, P(4)かP(8)に頂点7が含まれていることを確認します.
P(4) = 4 -> 3 -> 9
P(8) = 8 -> 7 -> 4 -> 3 -> 9
これをみると, P(8)に7が含まれてるので, 頂点8から頂点7までの部分パスであるP(8 , 7) = 8 -> 7が定義できます.
よって, P(v) = rev P(v , x) -> P(y)より
P(7) = rev P(8 . 7) -> P(4)
P(7) = 7 -> 8 -> 4 -> 3 -> 9
となります.
これも確認していると, M交互パスになっています.
nonouter label
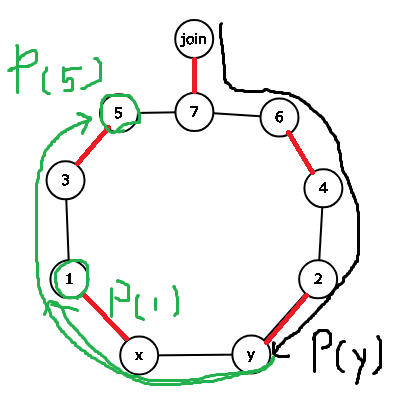
頂点1に注目してみましょう. グラフを見てみると, P(1), つまり頂点1から頂点9までのパスで, はじめの辺がマッチングされている辺であるM-交互パスはありません.
なのでnonouter labelが貼ってあります.
first[v]
P(v)上で一番最初のnonouterな頂点を持ちます, としか言えません....がこれによって$O(V^4)$から$O(V^3)$の改善がされます!(強い)
labelの貼り方
上のようにvertex label, edge label を貼るにはどうすればよいでしょうか.
探索中でouterな頂点xから伸びるマッチされていない辺(x,y)に注目しているとします. xはouterな頂点なので, P(x)が存在します.
もし, 頂点yがマッチされていないかつ, start labelではない頂点であれば, パスy -> P(x)はM-増加パスになるので増加操作をすれば良いです.
頂点yが頂点vとマッチされているとします.
頂点yがnonouterの場合
image
v -> y -> P(x)はマッチングされている辺から始まるM-交互パスです. なのでこのパスはP(v)として採用できます.
label[v] <- x(あとでP(v)を復元するため),
first[v] <- y(yはP(v)で初めて現れるnonouterな頂点なので) としてやります.
また頂点vはこの瞬間outerな頂点になったので, 頂点vから探索することが出来ます(実装ではこの頂点をBFSのQUEUEにenqueueしています)
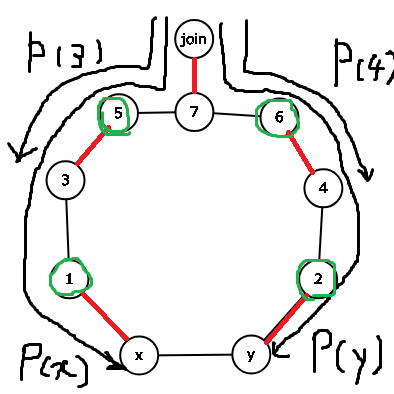
頂点yがouterな場合
この場合どうなるでしょうか? 実はこのような状態になっています.
緑で丸を付けている頂点はnonouterな頂点です. joinはP(x)とP(y)の共通部分で一番はじめのnonouterな頂点です.
左側のnonouterな頂点に注目します. これらの頂点はこのようにすることでouterになります.
つまり,頂点1と5のそれぞれのM-交互パス, P(1), P(5)はP(y)のパスとP(x)のパスを逆流したものを合わせたもので作ることができます.
そのため, この図の場合ではP(x),P(y)のパスを後で作るために, 1, 2, 5, 6, の頂点にnum(x,y)のedge labelを貼ります.
またnonouterからouterになった頂点はvertex labelの時と同様に探索範囲が広がるので, QUEUEにenqueueします.
実装
ではGabowの示した実装を紹介していきます. E AlgorithmはメインルーチンEと, サブルーチンL, Rからなります.
E
E では, マッチングしていない頂点uからBFSをして, 到達した頂点の性質に応じて処理をします.
E0 - 初期化
頂点を1...V, 辺をV+1...と番号付ける.
0をダミーの頂点とする.
0 <= i <= V を満たすiについて, label[i] <- -1 , mate[i] <- 0
u <- 0
E1 - BFS開始 - augment_check
u <- u + 1
u > V であれば, プログラムを終了する.
uがマッチングされている頂点(mate[v] != 0)であれば, E1に行く.
そうでなければ, uはBFSのスタートの頂点となる.
label[u] <- 0
first[u] <- 0
QUEUEにuをenqueueする.
E2 - 辺を取り出す.
QUEUEが空の場合, E1に行く.
QUEUEからdequeueした値をxとする.
- xyと表現できる辺に対して一つづつE3を実行する.
E3 - 増加操作
yがマッチングされていない頂点(mate[y] == 0)かつ, y != uであれば次を実行する.
mate[y] <- x としてサブルーチンR(x , y)を実行する. (M-増加パス "y -> P(x)"が増加される)
その後, 1) をbreakしてE7に行く
E4 - edge label 割り当て
yがouterな頂点であれば, Lを呼び出し, 1)をcontinueする.
E5 - vertex label 割り当て
mate[y]がnonouterな頂点であれば, label[mate[y]] <- x, first[mate[y]] <- y として, 1)をcontinueする.
E6 - 次の辺
1)をcontinueする.
E7 - BFS終了
0 <= i <= Vについて, label[i] <- i
E1に行く.
L - assignLabel
Lでは, P(x), P(v)上のnonouterな頂点にnum(xy)をラベルする.
P(x)とP(y)の共通部分で一番はじめのnonouterな頂点をjoinとしたとき, P(x)に沿ってxからjoinまでのnonouterな頂点にnum(xy)をラベルする.
yについても同様です.
これによって一部のnonouterな頂点がouterに変わり探索範囲が広がります.
L0 - 初期化
r <- first[x] , s <- first[y]
r == sであれば, return.
頂点vにflagを立てることをlabel[v] <- -num(xy)とする. labelの値がマイナスであればすべてnonouterな頂点なので,-num(xy)を代入しておいても問題はありません.
r , sにflagを立てる.
L1 - 入れ替え
s != 0 であれば, swap(r , s)
L2 - 次のnonouterな頂点に進む
r <- first[label[mate[r]]]
頂点rにフラグが立っていないならば, rにフラグを立ててL1に行く.
そうでなければ, join <- r としてL3にいく.
L3 - P(x), P(y)上のnonouterな頂点をラベルする
v <- first[x]としてL4を実行する.
v <- first[y]としてL4を実行する.
L5に行く.
L4 - v をラベルする.
v != joinであれば, QUEUEにvをenqueueして, label[v] <- num(xy) , first[v] <- join , v <- first[label[mate[v]]] としてL4を繰り返す.
そうでなければ, L3に戻る.
L5 - firstの更新
すべてのouterな頂点iに対してfirst[i]がouterな頂点であれば, first[i] <- joinとする.
L6 - L 終了
return
R(v , w) - Rematch
RはM-増加パスに沿ってマッチングし直して増加させる(rematch)サブルーチンです. 再帰的にRを呼び出すことでうまく増加させています.
R1 - vからwにマッチングする
t <- mate[v] , mate[v] <- w
mate[t] != vであれば, return
R2
vがvertex labelを持っているとき, mate[t] <- label[v]として R(label[v] , t)を呼び出す.
R3
vがedge labelを持っているとき, label[v] <- num(xy)として, R(x , y)を呼び出した後, R(y , x)を呼び出す.
ここから実装
上に書いたアルゴリズムをそのまま書くと一般マッチングを$O(V^3)$で解くプログラムが出来ます.
が、L5の処理を遅延評価すると$O(VElogV)$になることが知られています.(参考にしました)しかも定数倍がかなり早いです.
実装の注意
- 0はダミーな頂点として扱うため, Algorithmの最初にグラフを1-indexedに直さなければいけません
- outerな頂点vでは
label[v] >= 0です. - 下の実装では, L1~E6...augment_check, サブルーチンLをassignLabel, サブルーチンRをrematch, firstの遅延評価をeval_firstとしています.
- mateを復元すると, マッチングに使う辺までわかります.
# include <vector>
# include <cassert>
# include <set>
# include <queue>
# include <functional>
# include <algorithm>
struct edge {
int to;
int label;
};
::std::vector<::std::pair<int, int>> gabow_edmonds(const ::std::vector<::std::vector<int>>& gra){
// E0 - 初期化
int N = gra.size();
::std::vector<::std::vector<edge>> g(N + 1);
::std::vector<::std::pair<int, int>> edges;
{
int cnt = N + 1;
for(int i = 0;i < N;i++){
for(auto to : gra[i]){
if(i < to){
g[to + 1].push_back({i + 1, cnt});
g[i + 1].push_back({to + 1, cnt++});
edges.push_back({i + 1, to + 1});
}
}
}
}
::std::vector<int> mate(N + 1 , 0);
::std::vector<int> label(N + 1 , -1);
::std::vector<int> first(N + 1 , 0);
::std::queue<int> que;
// firstの遅延評価
::std::function<int(int)> eval_first = [&](int x){
if(label[first[x]] < 0) return first[x];
first[x] = eval_first(first[x]);
return first[x];
};
// サブルーチンR
::std::function<void(int, int)> rematch = [&](int v, int w){
// R1
int t = mate[v];
mate[v] = w;
if(mate[t] != v) return;
// R2
if(label[v] <= N){
mate[t] = label[v];
rematch(label[v] , t);
}
// R3
else{
int x = edges[label[v] - N - 1].first;
int y = edges[label[v] - N - 1].second;
rematch(x , y);
rematch(y , x);
}
};
::std::function<void(int, int, int)> assignLabel = [&](int x, int y, int num){
// L0
int r = eval_first(x);
int s = eval_first(y);
int join = 0;
if(r == s) return;
// -numがフラグ
label[r] = -num;
label[s] = -num;
while(true){
// L1
if(s != 0) ::std::swap(r , s);
// L2
r = eval_first(label[mate[r]]);
if(label[r] == -num){
join = r;
break;
}
label[r] = -num;
}
// L3
int v = first[x];
// L4
while(v != join){
que.push(v);
label[v] = num;
first[v] = join;
v = first[label[mate[v]]];
}
// L3
v = first[y];
// L4
while(v != join){
que.push(v);
label[v] = num;
first[v] = join;
v = first[label[mate[v]]];
}
// L5は遅延評価しているため不要
// L6
return;
};
::std::function<bool(int)> augment_check = [&](int u){
// E1 後半
first[u] = 0;
label[u] = 0;
que.push(u);
while(!que.empty()){
// E2
int x = que.front();
que.pop();
for(auto e : g[x]){
int y = e.to;
// E3
if(mate[y] == 0 && y != u){
mate[y] = x;
rematch(x , y);
return true;
}
// E4
else if(label[y] >= 0){
assignLabel(x , y , e.label);
}
// E5
else if(label[mate[y]] < 0){
label[mate[y]] = x;
first[mate[y]] = y;
que.push(mate[y]);
}
// E6
}
}
return false;
};
for(int i = 1;i <= N;i++){
// E1
que = ::std::queue<int>();
if(mate[i] != 0) continue;
if(augment_check(i)){
// E7
::std::fill(label.begin(), label.end(), -1);
}
}
::std::vector<::std::pair<int, int>> ans;
for(int i = 1;i <= N;i++){
if(i < mate[i]){
ans.push_back({i , mate[i]});
}
}
return ans;
}
使い方
ADABLOOM
これでverifyしました.
# include <bits/stdc++.h>
using namespace std;
using i64 = long long;
signed main(){
cin.tie(0);
ios::sync_with_stdio(false);
int T;
cin >> T;
for(int t = 0;t < T;t++){
int N;
cin >> N;
vector<vector<int>> g(N);
vector<i64> a(N);
for(int i = 0;i < N;i++) cin >> a[i];
for(int i = 0;i < N;i++){
for(int j = 0;j < N;j++){
i64 XOR = a[i] ^ a[j];
if(a[i] < XOR && XOR < a[j]){
g[i].push_back(j);
g[j].push_back(i);
}
}
}
cout << gabow_edmonds(g).size() << endl;
}
}
C - 2D Plane 2N Points
a[i] < c[j] && b[i] < d[j]を満たす赤い点iと青い点jでマッチングを組むわけですが,
これは上の条件を満たす2つの頂点に辺を引っ張ってGabow's E Algorithmを適用するだけで答えが得られます.(脳死)
# include <bits/stdc++.h>
using namespace std;
# define rep(i, s, e) for(int (i) = (s);(i) <= (e);(i)++)
int N;
int a[101];
int b[101];
int c[101];
int d[101];
int main(){
cin >> N;
rep(i, 0, N - 1) cin >> a[i] >> b[i] ;
rep(i, 0, N - 1) cin >> c[i] >> d[i];
vector<vector<int>> g(N * 2);
rep(i, 0, N - 1){
rep(j, 0, N - 1){
if(a[i] < c[j] && b[i] < d[j]){
g[i].push_back(j + N);
g[j + N].push_back(i);
}
}
}
cout << gabow_edmonds(g).size() << endl;
}
貪欲より圧倒的に楽ですね!
AOJ - Combine Two Elements
今年のRUPCで出題されたようです.
要素iと要素jを削除する操作はシンプルにマッチングで良いです.
要素iだけを削除する操作は, 要素iが他の要素とマッチング出来ないようにダミーの頂点i+Nにマッチングさせるようにすれば一般マッチングで解けます.
想定解は二部グラフらしいのですがGabow E Algorithmがあれば何も考えずに解けますね
# include <bits/stdc++.h>
using namespace std;
int main(){
int N, A, B;
cin >> N >> A >> B;
vector<int> a(N), b(N);
for(int i = 0;i < N;i++){
cin >> a[i] >> b[i];
}
vector<vector<int>> g(N * 2);
for(int i = 0;i < N;i++){
int t = abs(a[i] - b[i]);
if(t <= A || (B <= t && t <= 2 * A)){
g[i].push_back(i + N);
g[i + N].push_back(i);
}
}
for(int i = 0;i < N;i++){
for(int j = i + 1;j < N;j++){
int t = abs(a[i] + a[j] - b[i] - b[j]);
if(t <= A || (B <= t && t <= 2 * A)){
g[i].push_back(j);
g[j].push_back(i);
}
}
}
cout << gabow_edmonds(g).size() << endl;
}
終わりに
今回この記事を書くに当たって, 査読に関わっていただきました けんちょんさん, 熨斗袋さん, ももねさんにはとても感謝をしています. ありがとうございました.
グラフ抽象化でライブラリを書いている真っ最中です.よかったら見ていってください!
ありがとうございました