このページは何?
インベンス・ルービン『統計的因果推論』8.10節のゼロ過剰対数正規分布モデルの実装を説明します.特に,元の論文が書かれたときにはなかったであろうPolya-Gammaのテクニックを使って実装します.
内容まとめ
このページのざっくりのまとめは以下です.
- 対数正規分布は$y=0$となる確率が$0$なので,ゼロ過剰対数正規分布は$0$になる確率を決定するパラメータと対数正規分布のパラメータを独立にサンプリングできます.
- ベイズロジスティック回帰の部分はPolya-Gamma分布を使うと効率的にサンプリングできます.
- モデルベースの因果推論は平均因果効果だけでなく,因果効果の分布全体を推定できる点が便利ですね.
問題設定について
今回の問題設定ではNSWという職業訓練が収入に与える因果効果に興味があります.データはLalonde(1986)で使われたものを用います.
下は介入群の介入後(=1978年)の収入のヒストグラムと,対照群の同期間の収入のヒストグラムです.収入がまったくない人がかなりの数存在していることがわかると思います.
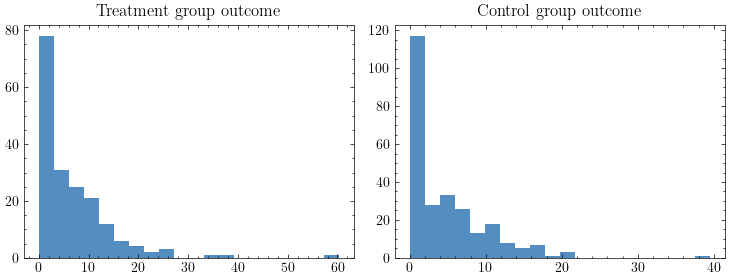
介入の有無と1978年の収入に加えて以下のような共変量も利用可能です.
- 年齢
- 教育年数
- 結婚しているかどうか
- 高校中退かどうか
- 民族性
- 1974年の収入(本では1974年の収入が0であるかどうかという変数も追加しています)
- 1975年の収入(上と同様に1975年の収入が0であるかどうかという変数も追加します)
モデル
前節で見た通り,今回のデータでは収入が全くない人がかなりの数いるため,対照群について,次のようなゼロ過剰対数正規分布でモデリングします.
\begin{align*}
p(y_i) &= (1-\pi_i)\delta(y_i) + \pi_i \mathcal{LN}(y_i; X_i \beta_c, \sigma_c^2), \\
\pi_i &= \frac{\exp(X_i^T\gamma_c)}{1 + \exp(X_i^T\gamma_c)}.
\end{align*}
ここで,$i$は個人のインデックスで,$y_i$がその個人の1978年時点の収入,$X_i$がその個人の共変量です.また,$\delta(y)$はデルタ関数で,$\mathcal{LN}(y; \mu, \sigma^2)$は平均パラメータ$\mu$,分散パラメータ$\sigma^2$の対数正規分布の確率密度関数です.
処置群についても以下のように同様にモデリングします.
\begin{align*}
p(y_i) &= (1-\pi_i)\delta(y_i) + \pi_i \mathcal{LN}(y_i; X_i \beta_t, \sigma_t^2), \\
\pi_i &= \frac{\exp(X_i^T\gamma_t)}{1 + \exp(X_i^T\gamma_t)}.
\end{align*}
事前分布は本に従って以下のように設定します.
\begin{align*}
\beta_c, \beta_t, \gamma_c, \gamma_t &\sim \mathcal{N}(0, 100^2 I_d), \\
\sigma_c^2, \sigma_t^2 &\sim \mathcal{IG}(1, 0.01).
\end{align*}
ここで,$d$は特徴量の次元で$I_d$は$d$次元の単位行列です.また,$\mathcal{N}(\mu, \Sigma)$は平均$\mu$,分散$\Sigma$の多変量正規分布で,$\mathcal{IG}(a, b)$はパラメータ$a, b$をもつ逆ガンマ分布です.
事後分布からのサンプリング
次に,事後分布からのサンプリング方法を説明します.対照群のパラメータ$\gamma_c, \beta_c, \sigma_c^2$と処置群のパラメータ$\gamma_t, \beta_t, \sigma_t^2$のサンプリング手順は同一なので,添字の$c$や$t$は省略します.
モデルは複雑に見えるかもしれませんが,事後分布からのサンプリングは意外に簡単です.なぜなら,
\begin{align*}
p(y|\gamma, \beta) &= \prod p(y_i | \gamma, \beta) \\
&= \prod (1-\pi_i)^{1-z_i} \pi_i^{z_i} \times \prod_{i:y_i>0} \mathcal{LN}(y_i; X_i \beta, \sigma^2)
\end{align*}
となって,$\gamma$に関する尤度と$\beta, \sigma^2$に関する尤度は独立に評価できるからです.ここで$z_i = 1(y_i>0)$です.少し丁寧に説明すると,$\beta, \sigma^2$の事後分布は
\begin{align*}
p(\gamma, \beta, \sigma^2 | y) &= \frac{p(\gamma)p(\beta)p(\sigma^2) \prod p(z_i | \gamma)\prod p(y_i | \beta, \sigma^2)}{\int p(\gamma)p(\beta)p(\sigma^2) \prod p(z_i | \gamma)\prod p(y_i | \beta, \sigma^2) d\gamma d\beta d\sigma^2} \\
&= \frac{p(\gamma)\prod p(z_i | \gamma)}{\int p(\gamma) \prod p(z_i | \gamma) d\gamma}\frac{p(\beta)p(\sigma^2) \prod p(y_i | \beta, \sigma^2) }{\int p(\beta)p(\sigma^2)\prod p(y_i | \beta, \sigma^2) d\beta d\sigma^2} \\
&= p(\gamma | y) p(\beta, \sigma | y)
\end{align*}
となり,$\gamma$の事後分布と$\beta, \sigma^2$の事後分布は独立に導出できます.
これは対数正規分布に限らず$y=0$である確率が$0$であるような分布であれば,成り立つ性質です.逆に言えば,ポアソン分布のように$y=0$である確率が$0$でないような分布では$y=0$になる確率を決定するパラメータとポアソン分布のパラメータが独立でないため,事後分布からのサンプリングはやや面倒になります.
以上を踏まえて,$\gamma$の事後分布と$\beta, \sigma^2$の事後分布からのサンプリング方法を説明します.
まず,$\gamma$については$z$を観測値としたベイズロジスティック回帰です.これはPolya-Gammaと呼ばれるテクニックを使うことで効率的にサンプリングできます.Polya-Gammaについては小林先生の説明やPolson et al. (2013)を参照してください.この手法では$\omega$という補助変数を追加してギブスサンプリングを行います.$\gamma$の事後分布は以下のようにサンプリングできます.
\begin{align*}
\omega_i | \gamma &\sim \mathcal{PG}(1, X_i^T\gamma), \\
\gamma | y, \omega &\sim \mathcal{N}(VX^T\kappa, V).
\end{align*}
ここで,$X$を共変量を並べた行列,$\Omega$を$\omega_i$を対角に並べた行列として,$V = (X^T\Omega X + 1 / 10000 I)^{-1}, \kappa_i = z_i - 1 / 2$です.また,$\mathcal{PG}(a, b)$はパラメータ$a, b$を持つPolya-Gamma分布です.
また,$\beta, \sigma^2$の事後分布からは以下のようにギブスサンプリングできます.
\begin{align*}
\beta | y, \sigma^2 &\sim N\left(\frac{1}{\sigma^2} \Sigma X \log(y), \Sigma\right), \\
\sigma^2 | y, \beta &\sim IG(1 + N_c / 2, 0.01 + (\log(y)-X^T\beta)^T(\log(y)-X^T\beta)/2).
\end{align*}
ここで$\Sigma = ((1 / \sigma^2) X^T X + (1 / 100^2) I_d)^{-1}$です.
以上記載した通り,$\gamma$と$\beta, \sigma^2$はほとんど解析的にギブスサンプリングできます.
実装
走り書きですが,上記のサンプリングを実装したコードが以下です.
import numpy as np
from scipy.stats import invgamma
from polyagamma import random_polyagamma
def gamma_sampler(z, X, num_samples, burn_in, thinning):
"""
gammaをサンプリングする関数
z: 観測値が0より大きければ1,そうでなければ0をとる値
X: 共変量を並べた行列
num_samples: サンプル数
burn_in: バーンインとして無視するサンプル数
thinning: サンプルの自己相関を小さくするために間引くサンプル数
"""
d = X.shape[1]
kappa = z - 0.5
gamma_samples = np.zeros((num_samples, d))
gamma = np.zeros(d)
for i in range(num_samples+burn_in):
for _ in range(thinning):
w = random_polyagamma(1, X @ gamma)
W = np.diag(w)
posterior_var_gamma = np.linalg.inv(X.T @ W @ X + 1 / 10000 * np.eye(d))
posterior_mean_gamma = posterior_var_gamma @ X.T @ kappa
gamma = np.random.multivariate_normal(mean=posterior_mean_gamma, cov=posterior_var_gamma)
if i + 1 > burn_in:
gamma_samples[i - burn_in, :] = gamma
return gamma_samples
def beta_sigma2_sampler(y, X, num_samples, burn_in, thinning):
"""
betaとsigma^2をサンプリングする関数
y: 観測値
X: 共変量を並べた行列
num_samples: サンプル数
burn_in: バーンインとして無視するサンプル数
thinning: サンプルの自己相関を小さくするために間引くサンプル数
"""
lny = np.log(y)
N, d = X.shape
beta_samples = np.zeros((num_samples, d))
sigma2_samples = np.zeros(num_samples)
beta = np.zeros(d)
sigma2 = 1
for i in range(num_samples+burn_in):
for _ in range(thinning):
# betaのサンプリング
posterior_var_beta = np.linalg.inv(1 / sigma2 * X.T @ X + 1 / 10000 * np.eye(d))
posterior_mean_beta = 1 / sigma2 * posterior_var_beta @ X.T @ lny
beta = np.random.multivariate_normal(mean=posterior_mean_beta, cov=posterior_var_beta)
# sigma^2のサンプリング
posterior_a_sigma2 = 1 + N / 2
posterior_b_sigma2 = 0.01 + 1 / 2 * (lny - X @ beta).T @ (lny - X @ beta)
sigma2 = invgamma(a=posterior_a_sigma2, scale=posterior_b_sigma2).rvs()
if i + 1 > burn_in:
beta_samples[i - burn_in, :] = beta
sigma2_samples[i - burn_in] = sigma2
return beta_samples, sigma2_samples
上記のコード実行方法は以下です.
import pandas as pd
# データのインポート
nsw_data = pd.read_stata("https://users.nber.org/~rdehejia/data/nsw_dw.dta")
# データを本に記載のものと揃える
nsw_data['re74'] = nsw_data['re74'] / 1000
nsw_data['re75'] = nsw_data['re75'] / 1000
nsw_data['re78'] = nsw_data['re78'] / 1000
nsw_data['intercept'] = 1.0
nsw_data['re74=0'] = (nsw_data['re74']==0).astype(int)
nsw_data['re75=0'] = (nsw_data['re75']==0).astype(int)
# yが0より大きいかそうでないかを表す値を取得
nsw_data['z'] = (nsw_data['re78']>0).astype(int)
z_c = nsw_data[nsw_data['treat']==0]['z'].values
z_t = nsw_data[nsw_data['treat']==1]['z'].values
# 共変量として使うカラム一覧
col_features = [
'intercept',
'age',
'education',
'married',
'nodegree',
'black',
're74',
're74=0',
're75',
're75=0'
]
# gammaのサンプリングで使う共変量を取得
X_gamma_c = nsw_data[nsw_data['treat']==0][col_features].values
X_gamma_t = nsw_data[nsw_data['treat']==1][col_features].values
# beta, sigma^2のサンプリングで使う共変量を取得
X_beta_c = nsw_data[(nsw_data['treat']==0)&(nsw_data['z']==1)][col_features].values
X_beta_t = nsw_data[(nsw_data['treat']==1)&(nsw_data['z']==1)][col_features].values
# 観測値を取得
y_c = nsw_data[(nsw_data['treat']==0)&(nsw_data['z']==1)]['re78'].values
y_t = nsw_data[(nsw_data['treat']==1)&(nsw_data['z']==1)]['re78'].values
# サンプリングの実行
num_samples = 4000
burn_in = 100
thinning = 100
gamma_c_samples = gamma_sampler(z_c, X_gamma_c, num_samples, burn_in, thinning)
gamma_t_samples = gamma_sampler(z_t, X_gamma_t, num_samples, burn_in, thinning)
beta_c_samples, sigma2_c_samples = beta_sigma2_sampler(y_c, X_beta_c, num_samples, burn_in, thinning)
beta_t_samples, sigma2_t_samples = beta_sigma2_sampler(y_t, X_beta_t, num_samples, burn_in, thinning)
結果
$\gamma, \beta, \sigma^2$を事後分布からサンプリングすれば,反実仮想の予測を行うことで因果効果を推定できます.ベイズ的なモデルベースの因果推論の優れた点はユニット単位の因果効果を不確実性付きで推定できるため,用途に応じて,様々な統計量を算出できる点です.
例えば以下は平均・25%点・50%点・75%点に対する因果効果のヒストグラムです.
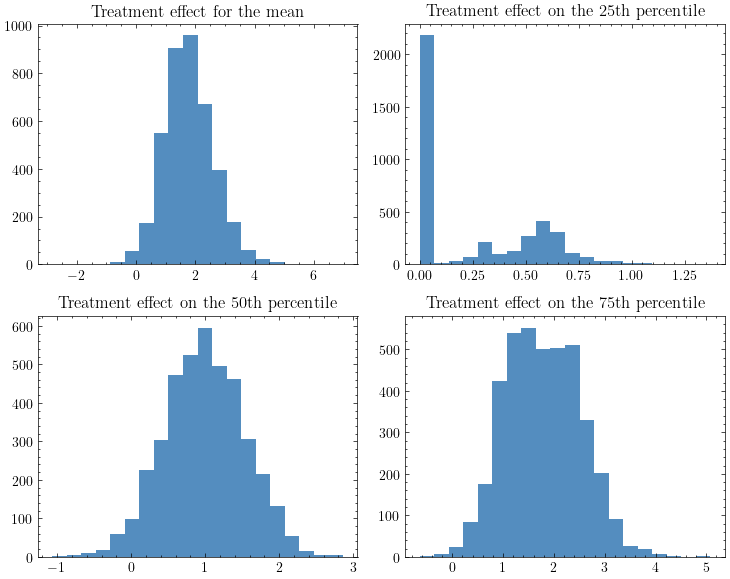
ちなみに,この結果は松浦さんの実装とは結果が一致していますが,本とはやや一致しません.
余談
- 上記の通り,モデルベースの因果推論は用途に応じて様々な統計量を算出できますし,確率的な最適化も可能になるため,もっと利用されて良いように思います.本ではモデル誤特定に対してナイーブである欠点が指摘されていますが,以下のような点を考えると必ずしも欠点ではないように思います.
- 現代においてはBARTやガウス過程などかなり柔軟なモデルが登場している.
- 傾向スコアベースの因果推論も結局は傾向スコアを推定するために使うモデルに依存する.
- モデルベースであれば,観測値の範囲内ではあるものの交差検証でモデルチェックできる.
- 本に記載されている結果が一致しないという現象は25章の再現でも発生しました.どちらも松浦さんの実装とは結果が一致していることを考えると,この本に記載されている結果のいくつかはかなり怪しいのではないかと考えています.いずれにせよコードを公開すべきだと思います.
- 今年の統計関連学会連合大会において,私が直接聞いた講演に限定しても,3講演でPolya-Gammaを利用していたため,ベイジアンにとってはPolya-Gammaは常識になり始めているように思います.