ベイズによる縮小推定(2)

　3回にわけて、ベイズモデルによる縮小推定の手法について解説する。今回は、Horseshoe Priorとその拡張したモデルについて説明する。

1. ベイズによる縮小推定(1)
2. ベイズによる縮小推定(2)
3. ベイズによる縮小推定(3)（執筆中）

4. Horseshoe

4.1 Horseshoe

　spike-and-slabの欠点として、計算負荷が高いことなどがあげられる。そこで、階層的なモデルにより、密度が0付近に集中しており、かつ、裾の重い分布を実現する方法が提案されている。

　その中で最も代表的なモデルは、Horseshoe prior(馬蹄事前分布)である¹。Horseshoe priorについては、日本語でも松浦さんや菅澤さんの詳しい説明がある²³ため、ここでは簡単に、重要な性質についていくつか説明する。

　まず、Horseshoe Priorとは以下のようなモデルである。

\displaylines{
\theta_i \sim \mathcal{N}(0, \lambda_i^2 \tau^2) \\
\lambda_i \sim {\rm C}^+ (0, 1)
}

ここで、${\rm C}^+ (0, 1)$は平均0、スケールファクター1の半コーシー分布である。また、$\tau$はGlobal Shrinkage Parameterと呼ばれるパラメータである。

　この$\theta_i$の周辺分布は、まず、

\lim_{\theta \rightarrow 0} \pi (\theta) = \infty

である¹。つまり、$0$付近で$\theta_i$の事前分布は発散する。また、$\tau=1, \theta \neq 0$で、

\frac{1}{2\sqrt{2\pi^3}}\log(1+\frac{4}{\theta^2}) < \pi(\theta) < \frac{1}{\sqrt{2\pi^3}} \log(1+\frac{2}{\theta^2})

である。$\epsilon\rightarrow0$で$\log(1+\epsilon)\approx\epsilon$であることから、おおよそ$1/\theta^2$のオーダーで裾の重さが減衰する。正規分布やラプラス分布が指数的に裾が軽くなることを考えると、非常に重い裾をもっていることがわかる。

　また、Horseshoe Prior(というより縮小推定)について考える場合には、Shrinkage Factorを考えると良い。以下では、$\tau=1$を仮定する。$\kappa_i = 1/(1+\lambda_i^2)$として、

\mathbb{E}[\theta_i|y_i] = (1-\mathbb{E}[\kappa_i|y_i])y_i

となる。この式から、$\mathbb{E}[\kappa_i|y_i]$が$1$に近いとき$\theta_i$は$0$に近い値をとり、$\mathbb{E}[\kappa_i|y_i]$が$0$に近いとき、$\theta_i$は$y_i$に近い値をとることがわかる。このような$\kappa_i$をShrinkage Factorとよぶ。

　Horseshoe Priorのもとで、$\kappa_i$の事前分布は、ベータ分布$Beta(1/2, 1/2)$となる。$Beta(1/2, 1/2)$の確率密度関数は下のグラフのようになる。

　グラフから、$0$と$1$に確率密度が集中していることがわかる。つまり、縮小する値は縮小し、保存する値はそのまま保存するような性質をもつ。確率密度関数が馬の蹄のようにみえることから、Horseshoe(馬蹄)とよばれる。

　Horseshoeはstanなどで簡単に実装できる（ただし収束しない場合がある）。実装する詳細なモデルは次である。

\displaylines{
\theta_i \sim \mathcal{N}(0, \lambda_i^2 \tau^2) \\
\lambda_i \sim {\rm C}^+ (0, 1) \\
\tau \sim {\rm C}^+ (0, 10)
}

code_hs = '''
data {
  int N;
  real Y[N];
}
parameters {
  vector[N] theta;
  real<lower=0> tau;
  vector<lower=0>[N] lambda;
}
model {
  Y ~ normal(theta, 1);
  theta ~ normal(0, tau*lambda);
  lambda ~ cauchy(0, 1);
  tau ~ cauchy(0, 10);
}
'''

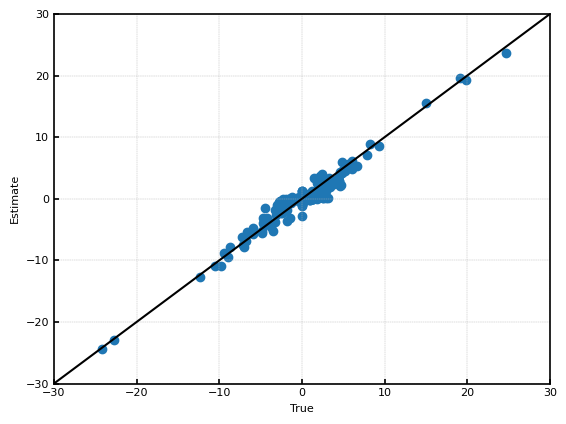
　推定結果を示す。$\sqrt{\frac{1}{n}\sum(\hat{\theta}_i-\theta_i)^2}$は約$0.54$程度であったため、spike-and-slabと比較して10%程度推定結果が改善した。

4.2 Horseshoe+

　階層を深くすることで、Horseshoeをさらに0付近に密度を集中させ、裾を重くしたモデルがHorseshoe+である⁴。Horseshoe+は以下のようなモデルである。

\displaylines{
\theta_i \sim \mathcal{N}(0, \lambda_i^2) \\
\lambda_i \sim {\rm C}^+ (0, \tau \eta_i) \\
\eta_i \sim {\rm C}^+ (0, 1)
}

　Horseshoe+では$\tau=1$で、

\frac{1}{\pi^2\sqrt{2\pi}}\log(1+\frac{4}{\theta^2}) < \pi(\theta) \leq \frac{1}{\pi^2|\theta|}

である。この式から、Horseshoeと同様に重い裾をもっていることがわかる。

　また、$\kappa_i$の事前分布は$\tau=1$で、

p(\kappa_i) \propto \kappa_i^{-\frac{1}{2}} (1-\kappa_i)^{-\frac{1}{2}} \frac{\log(1-\kappa_i)-\log(\kappa_i)}{1-2\kappa_i}

となる。$\log(1-\kappa_i)-\log(\kappa_i)$が$0$や$1$に近いところで発散することより、Horseshoeよりも$0$や$1$に密度がより集中していることがわかる。

　Horseshoe+もstanにより、簡単に実装できる（ただし収束しない場合がある）。実装する詳細なモデルは次である。

\displaylines{
\theta_i \sim \mathcal{N}(0, \lambda_i^2) \\
\lambda_i \sim {\rm C}^+ (0, \tau \eta_i) \\
\eta_i \sim {\rm C}^+ (0, 1) \\
\tau \sim {\rm C}^+ (0, 10)
}

code_hsp = '''
data {
  int N;
  real Y[N];
}
parameters {
  vector[N] theta;
  real<lower=0> tau;
  vector<lower=0>[N] lambda;
  vector<lower=0>[N] eta;
}
model {
  Y ~ normal(theta, 1);
  theta ~ normal(0, lambda);
  lambda ~ cauchy(0, tau*eta);
  eta ~ cauchy(0, 1);
  tau ~ cauchy(0, 10);
}
'''

　推定結果を示す。$\sqrt{\frac{1}{n}\sum(\hat{\theta}_i-\theta_i)^2}$は約$0.54$程度であったため、Horseshoeとほとんど推定性能は変わらなかった。

4.3 Heavy Tailed Horseshoe

　プレプリントであるが（2021年11月現在）、Heavy Tailed HorseshoeというHorseshoe Priorよりも裾の重い分布も提案されている⁵。プレプリントであるため、簡単な紹介にとどめる。Heavy Tailed Horseshoeは以下のようなモデルである。

\displaylines{
\theta_i \sim \mathcal{N}(0, \frac{\tau^2}{\gamma_i}) \\
\gamma_i \sim {\rm Gamma}(p_i, \omega_i) \\
\omega_i \sim {\rm Gamma}(1- p_i, 1) \\
p_i \sim \pi(p_i)
}

$\pi(p_i)$として例えば、一様分布${\rm Uniform}(0, 1)$などが提案されている。

　上の定式化はHorseshoeと大きく異なるように見えるかもしれないが、Horseshoeも

\displaylines{
\theta_i \sim \mathcal{N}(0, \frac{\tau^2}{\gamma_i}) \\
\gamma_i \sim {\rm Gamma}(1/2, \omega_i) \\
\omega_i \sim {\rm Gamma}(1/2, 1)
}

と書くことができる。

　Heavy Tailed Horseshoeの重要な性質として、Horseshoeの周辺分布の裾の重さは$|\theta_i|\rightarrow \infty$で、$\frac{1}{\theta_i^2}$のオーダーであるのに対し、Heavy Tailed Horseshoeは$\frac{1}{\theta_i\log(|\theta_i|)^2}$程度であるため、Horseshoeよりも裾が重いことがわかる。

　また、$\kappa_i$の事前分布は$\tau=1$で、

p(\kappa_i) \propto \frac{\kappa_i^{-1} (1-\kappa_i)^{-1}}{\log((1-\kappa_i)/\kappa_i)^2+\pi^2}

となる。この式から、Horseshoeよりも$0$と$1$に密度がより集中していることがわかる。

　さらに、Horseshoeに対するHorseshoe+のように、Heavy Tailed Horseshoeに対するHeavy Tailed Horseshoe+も論文の中では提案されている。

1. CARVALHO, C. M., POLSON, N. G., & SCOTT, J. G. (2010). The horseshoe estimator for sparse signals. Biometrika, 97(2), 465–480. ↩ ↩²

2. https://statmodeling.hatenablog.com/entry/shrinkage-factor-and-horseshoe-prior ↩

3. https://qiita.com/ssugasawa/items/400db3438d3706292f33 ↩

4. Bhadra, A. & Datta, J, & Polson, N. & Willard, B.. (2017). The Horseshoe+ Estimator of Ultra-Sparse Signals. Bayesian Analysis. 12(4). 1105 - 1131. ↩

5. Womack, A. & Yang, Z..(2019). Heavy Tailed Horseshoe Priors. arXiv preprint arXiv:1903.00928 ↩