3回にわけて、ベイズモデルによる縮小推定の手法について解説する。今回は、縮小推定のモチベーションや問題設定・Bayesian Lasso・spike-and-slabについて、説明する。
- ベイズによる縮小推定(1)
- ベイズによる縮小推定(2)
- ベイズによる縮小推定(3)(執筆中)
1. 縮小推定のモチベーション
以下では、$n$個の観測値$y_i$が平均$\theta_i$、分散$1$の正規分布
y_i \sim N(\theta_i, 1)
に従い、観測値から$\theta_i$を推定する問題を考える。$\theta_i$は、ほとんどが$0$に近い値をとるが、いくつかは大きな値をとるとする。このような問題設定では、推定値を$0$に縮小しつつ、大きな値はそのまま残すような推定を行いたい。ここでは、縮小推定を扱うが、スパース推定・小地域推定・変数選択・正則化などの分野でも同様のモチベーションがある。
ベイズモデルによってこのような推定を実現するためには、密度が0付近に集中しており、かつ、裾の重い分布を$\theta_i$の事前分布として用いる方法がある。以下では、そのような事前分布を紹介する。
2. Bayesian Lasso
縮小推定のために用いられる最も代表的な事前分布はラプラス分布(二重指数分布)だろう。このようなモデルをBayesian Lassoとよぶ。よく知られているようにラプラス分布を事前分布として設定した場合のMAP推定はL1正則化を導く。
stanによりBayesian Lassoを実装する。具体的なモデルは以下である。
\displaylines{
y_i \sim N(\theta_i, 1) \\
\theta_i \sim L(0, \tau_i^2) \\
\tau_i^2 \sim IG(5, 50)
}
ここで、$L$はラプラス分布であり、$IG$は逆ガンマ分布である。このモデルのstanによる実装は以下である。
code_laplace = '''
data {
int N;
real Y[N];
}
parameters {
real theta[N];
real<lower=0> tau[N];
}
model {
Y ~ normal(theta, 1);
theta ~ double_exponential(0, sqrt(tau));
tau ~ inv_gamma(5, 50);
}
'''
また、推定性能を調べる問題設定は以下である1。
\displaylines{
y_i \sim N(\theta_i, 1) \\
\theta_i \sim p_it_3(0, 3) + (1-p_i)\delta_0\\
p_i \sim Beta(1, 4)
}
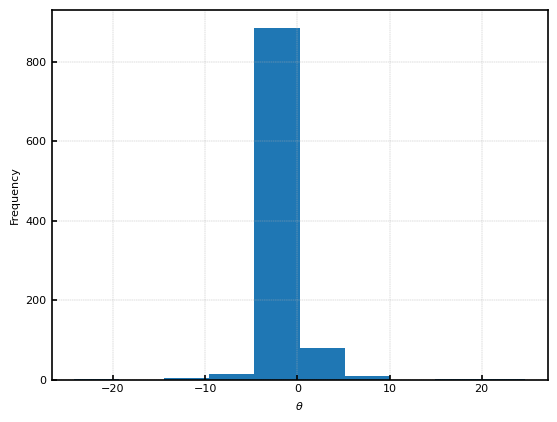
ここで、$t_3$は自由度$3$のt分布、$Beta(1, 4)$はベータ分布、$\delta_0$はディラックのデルタ関数である。生成した1000個の$\theta_i$のヒストグラムを示す。ほとんどが$0$に集中しているが、$-20$から$20$まで薄く分布していることがわかる。
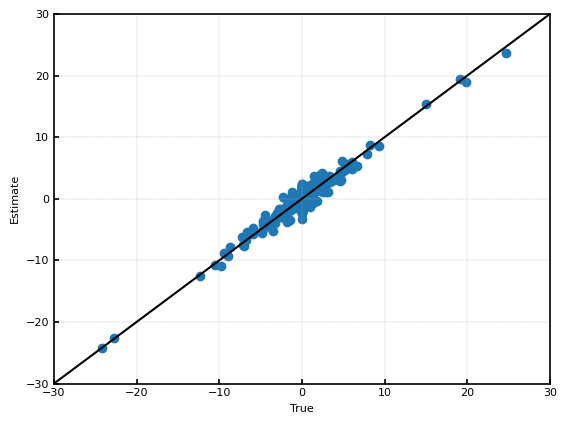
Bayesian Lassoによる推定結果を示す。横軸が真値で縦軸が推定値(事後分布の平均値)であり、完全に推定に成功している場合は45度線上にくる。下の図から、ある程度推定に成功しているが、0付近で推定がばらついていることがわかる。
事後分布の平均値を$\hat{\theta}_i$として、$\sqrt{\frac{1}{n}\sum(\hat{\theta}_i-\theta_i)^2}$により、推定性能を評価する。Bayesian Lassoの$\sqrt{\frac{1}{n}\sum(\hat{\theta}_i-\theta_i)^2}$は、約$0.83$である。$y_i \sim N(\theta_i, 1)$であることを考えると、$y_i$をそのまま推定値に用いるよりもわずかに性能が改善している。
実は、ラプラス分布は裾が$e^{-|x|}$のオーダーで減衰するため裾が薄く、$0$付近の密度の集中も弱い。以下で見る分布は基本的にラプラス分布よりも0付近に密度が集中しており、裾が重い。
3. spike-and-slab
縮小推定の単純なアイデアとして、$0$に集中した分布(これをspikeとよぶ)と裾の重い分布(これをslabとよぶ)の混合分布を使うという方法が考えられる。このような分布のことをspike-and-slabと呼ぶ2。この手法は1980年代に提案され、一つのスタンダードな手法となっている。例えば、Rのベイズ構造時系列パッケージのbstsでも採用されている3。
spikeとしては、ディラックのデルタ関数を用いる場合が最も多いようだが、分散の小さい正規分布やラプラス分布と分散の大きい正規分布やラプラス分布の混合分布を使う場合もある45。
Ishwaran et al.(2005)を参考に、以下のような分散の小さい正規分布と分散の大きい正規分布の混合分布をstanにより実装する。
\displaylines{
y_i \sim N(\theta_i, 1) \\
\theta_i \sim p_i N(0, \tau_i^2) + (1-p_i) N(0, v_0\tau_i^2)\\
\tau_i^2 \sim IG(5, 50) \\
p_i \sim Beta(1, 1)
}
ここで、$v_0$は$0.005$とした。stanによる実装は以下である。
code_sas = '''
data {
int N;
real Y[N];
real v0;
}
parameters {
real theta[N];
real<lower=0, upper=1> p[N];
real<lower=0> tau[N];
}
model {
Y ~ normal(theta, 1);
for (n in 1:N)
target += log_sum_exp(log(1-p[n]) + normal_lpdf(theta[n] | 0, sqrt(v0*tau[n])),
log(p[n]) + normal_lpdf(theta[n] | 0, sqrt(tau[n])));
tau ~ inv_gamma(5, 50);
}
'''
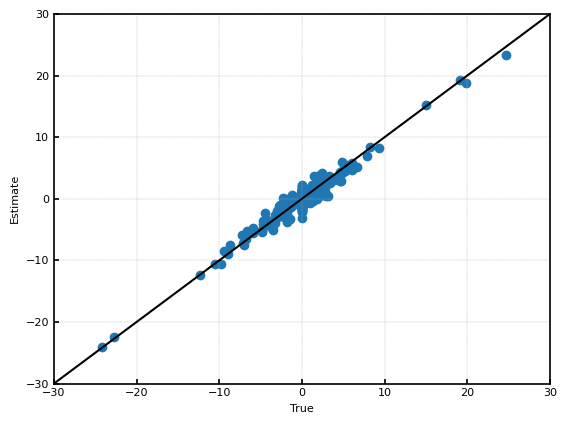
推定結果を示す。このグラフからはBayesian Lassoと推定結果の違いがあまり分からない。
しかし、$\sqrt{\frac{1}{n}\sum(\hat{\theta}_i-\theta_i)^2}$は約$0.60$であり、Bayesian Lassoに比べて、大きく推定性能が改善した。
-
CARVALHO, C. M., POLSON, N. G., & SCOTT, J. G. (2010). The horseshoe estimator for sparse signals. Biometrika, 97(2), 465–480. ↩
-
Mitchell, T. J., & Beauchamp, J. J. (1988). Bayesian Variable Selection in Linear Regression. Journal of the American Statistical Association, 83(404), 1023–1032. ↩
-
Scott, S. L., & Varian, H. R. (2014). Predicting the present with bayesian structural time series. International Journal of Mathematical Modelling and Numerical Optimisation, 5, 4-23. ↩
-
Ishwaran, H. & Rao, J.. (2005). Spike and slab variable selection: Frequentist and Bayesian strategies. The Annals of Statistics, 33(2), 730 - 773. ↩
-
Veronika Ročková and Edward I. George. (2018). The Spike-and-Slab LASSO. Journal of the American Statistical Association, 113:521, 431-444. ↩