#はじめに
以前Q学習についての記事を書いた。そこでは具体的な例として2椀バンディット問題を紹介したがそれは時間発展のない(状態が変わらない)ものであるので時間発展のある問題である倒立振子問題を紹介する。以前の記事とは独立した内容であるのでそれを読む必要はない。
コードはPython3.8.6で書いた。
#ε-greedy法
初めにε-greedy法を説明する。学習の初期段階ではQ値をランダムに生成するため、初期値に依存した決まった行動しか行わずうまく学習できないということがある(Q値のある値が大きく生成され、その地点では決まった行動しかしないなど)。ε-greedy法は以上の問題を解決するための方法の一つである。具体的には確率εでランダムな行動を選択し、確率$(1-\epsilon)$でQ値が最大の行動を選択するものだ。ランダムな行動を起こすこととQ値が最大になるような行動を起こすことはトレードオフの関係になっており、ランダムな行動を起こす回数が増えると学習がうまく進まなくなり、Q値が最大になるような行動を起こす回数が増えると広い範囲の捜索ができなくなる。学習の前半ではランダムな行動を多く起こして多く探索し、学習の終盤ではQ値が最大になるような行動を多く起こして活用を増やすことが理想的である。そのため、εの値を学習が進むにつれて小さくするようにするとより効率よく学習できる。
CartPole
CartPoleとはOpenAI Gymが提供しているゲーム環境の一つで倒立振子に関するゲームである。倒立振子問題とは台車の上に回転軸が固定された棒を立て、台車を左右に動かすことによって棒が倒れないように制御する問題である。CartPoleの様子は以下の通り。
OpenAI Gymのインストールは以下のように行う。
pip install gym
インストール後以下のコードを実行して正常に動くか確認する。
import gym
# 環境の生成
env = gym.make('CartPole-v0')
# 環境の初期か
observation = env.reset()
for t in range(1000):
# 現在の状況を表示させる
env.render()
# サンプルの行動をさせる 返り値は左から台車および棒の状態、得られた報酬、ゲーム終了フラグ、詳細情報
observation, reward, done, info = env.step(env.action_space.sample())
if done:
print("Finished after {} timesteps".format(t+1))
break
# 環境を閉じる
env.close()
私の場合(MacOS Big Sur ver11.1)ImportEroorが起きたが、以下のライブラリをインストールすることで解決できた。
pip install pyglet==1.5.11
次にOpenAI GymにおけるCartPoleについて説明する。
まず台車および棒についての条件は以下の通りである。
・台車の位置:$-2.4\sim2.4$
・台車の速度:$-\inf\sim\inf$
・棒の角度:$-41.8\sim 41.8$
・棒の先端の速度:$-\inf\sim\inf$
これらの初期値はどれも$-0.05\sim 0.05$の間でランダムに生成された数値である。
この環境に対する行動は以下の二つである。
1.台車を左に押す
2.台車を右に押す
報酬はステップごとに「1」与えられ、エピソードが終わる条件は以下の三つである。
1.棒の角度の絶対値が12°以上になる
2.台車の位置の絶対値が2.4以上になる
3.エピソードが200ステップを越える。
学習を完了と見なす条件は100回の連続した試行で195以上の報酬を得られた時である。
より正確に知りたければ条件元であるこれを見ると良い。
##実装(Q学習)
Q学習で棒が倒れないようなQテーブル(各状態と各行動に対応するQ値が書かれた表)を作成する。実装をメイン、エージェント、環境、状態(ブレイン)にわけて行う。
###状態(ブレイン)
まず状態に関するコードついて説明する。ここではQテーブルの更新や行動選択、観測した状態の離散化を行う。観測した状態の離散化はそのままの情報でであると連続した値を持ち無数の状態があるためQテーブルのサイズが大きくなり、学習が困難となるために行う。
import numpy as np
# 各状態の分割数
NUM_DIZITIZED = 6
# 学習パラメータ
GAMMA = 0.99 # 時間割引率
ETA = 0.5 # 学習係数
class State:
def __init__(self, num_states, num_actions):
# 行動数を取得
self.num_actions = num_actions
# Qテーブルを作成 (分割数^状態数)×(行動数)
self.q_table = np.random.uniform(low=-1, high=1, size=(
NUM_DIZITIZED**num_states, num_actions))
def bins(self, clip_min, clip_max, num):
# 観測した状態デジタル変換する閾値を求める
return np.linspace(clip_min, clip_max, num + 1)[1:-1]
def analog2digitize(self, observation):
#状態の離散化
cart_pos, cart_v, pole_angle, pole_v = observation
digitized = [
np.digitize(cart_pos, bins=self.bins(-2.4, 2.4, NUM_DIZITIZED)),
np.digitize(cart_v, bins=self.bins(-3.0, 3.0, NUM_DIZITIZED)),
np.digitize(pole_angle, bins=self.bins(-0.5, 0.5, NUM_DIZITIZED)),
np.digitize(pole_v, bins=self.bins(-2.0, 2.0, NUM_DIZITIZED))
]
return sum([x * (NUM_DIZITIZED**i) for i, x in enumerate(digitized)])
def update_Q_table(self, observation, action, reward, observation_next):
# 状態の離散化
state = self.analog2digitize(observation)
state_next = self.analog2digitize(observation_next)
Max_Q_next = max(self.q_table[state_next][:])
# Qテーブルを更新(Q学習)
self.q_table[state, action] = self.q_table[state, action] + \
ETA * (reward + GAMMA * Max_Q_next - self.q_table[state, action])
def decide_action(self, observation, episode):
# ε-greedy法で行動を選択する
state = self.analog2digitize(observation)
epsilon = 0.5 * (1 / (episode + 1))
if epsilon <= np.random.uniform(0, 1):
# 最も価値の高い行動を行う。
action = np.argmax(self.q_table[state][:])
else:
# 適当に行動する。
action = np.random.choice(self.num_actions)
return action
Qテーブルの初期値はそれぞれ-1~1でランダムに生成させる(0~1でもいい)。離散化に関する処理は台車および棒の条件に即して行う。先ほど紹介したε-greedy法を採用して、εは学習が進むごとに小さくなるようにする。
###エージェント
エージェントに関するコードでは先ほどの状態のコードを呼び出してQテーブルの更新や、行動の選択を行う。
from state import State
class Agent:
def __init__(self, num_states, num_actions):
# 環境を生成
self.state = State(num_states, num_actions)
def update_Q_function(self, observation, action, reward, observation_next):
# Qテーブルの更新
self.state.update_Q_table(observation, action, reward, observation_next)
def get_action(self, observation, step):
# 行動
action = self.state.decide_action(observation, step)
return action
###環境
環境に関するコードでは学習完了の条件や最終的にできたモデルのプレイ動画、報酬をエピソードごとの描画に関する処理を新たに加えエージェントのコードを呼び出すことで学習を行う。試行回数は1000にしたが、学習が終わらない場合試行回数を増やすと良い。
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import animation
import gym
from agent import Agent
# 最大のステップ数
MAX_STEPS = 200
# 最大の試行回数
NUM_EPISODES = 1000
class Environment():
def __init__(self, toy_env):
# 環境を生成
self.env = gym.make(toy_env)
# 状態数を取得
num_states = self.env.observation_space.shape[0]
# 行動数を取得
num_actions = self.env.action_space.n
# Agentを生成
self.agent = Agent(num_states, num_actions)
def run(self):
complete_episodes = 0 # 成功数
step_list = []
is_episode_final = False # 最後の試行
frames = [] # 画像を保存する変数
# 試行数分繰り返す
for episode in range(NUM_EPISODES):
observation = self.env.reset() # 環境の初期化
for step in range(MAX_STEPS):
# 最後の試行のみ画像を保存する。
if is_episode_final:
frames.append(self.env.render(mode='rgb_array'))
# 行動を求める
action = self.agent.get_action(observation, episode)
# 行動a_tの実行により、s_{t+1}, r_{t+1}を求める
observation_next, _, done, _ = self.env.step(action)
# 報酬を与える
if done: # ステップ数が200経過するか、一定角度以上傾くとdoneはtrueになる
if step < 195:
reward = -1 # 失敗したので-1の報酬を与える
complete_episodes = 0 # 成功数をリセット
else:
reward = 1 # 成功したので+1の報酬を与える
complete_episodes += 1 # 連続成功記録を更新
else:
reward = 0
# Qテーブルを更新する
self.agent.update_Q_function(observation, action, reward, observation_next)
# 観測の更新
observation = observation_next
# 終了時の処理
if done:
step_list.append(step+1)
break
if is_episode_final:
es = np.arange(0, len(step_list))
plt.plot(es, step_list)
plt.savefig("cartpole.png")
plt.figure()
patch = plt.imshow(frames[0])
plt.axis('off')
def animate(i):
patch.set_data(frames[i])
anim = animation.FuncAnimation(plt.gcf(), animate, frames=len(frames),
interval=50)
anim.save('movie_cartpole_v0.mp4', "ffmpeg")
break
# 10連続成功したら最後の試行を行う
if complete_episodes >= 100:
print('100回連続成功')
is_episode_final = True
###メイン
環境のコードを呼び出して学習を行う。
from env import Environment
TOY = "CartPole-v0"
def main():
cartpole = Environment(TOY)
cartpole.run()
if __name__ == "__main__":
main()
###結果
最終的に以下のようにCartPoleを制御できた。
報酬は以下のように遷移していった。
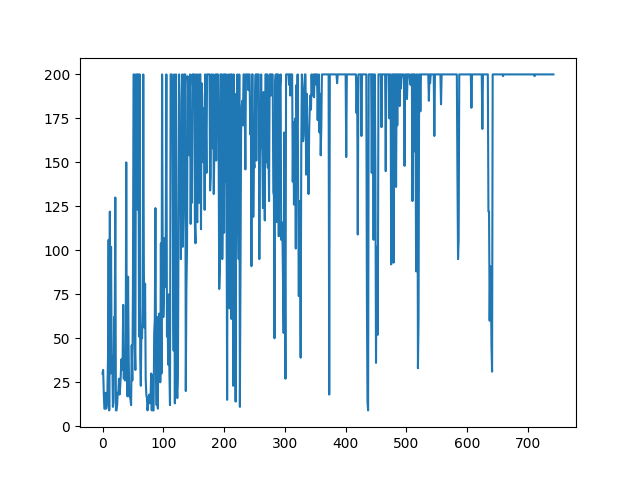
今回のコードでは学習が完了すると学習を止めるが、止めずに続けると報酬の様子は以下のようになる。
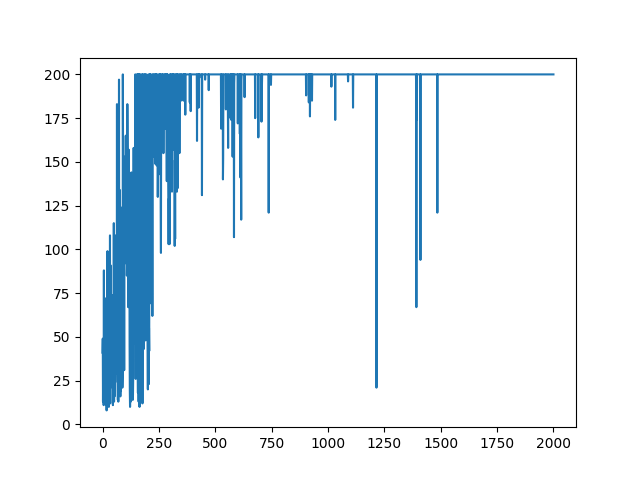
時間経過してもたまに失敗してしまうことが分かる。次に直近100エピソードの報酬の平均およびそのばらつき(標準偏差)を見る。
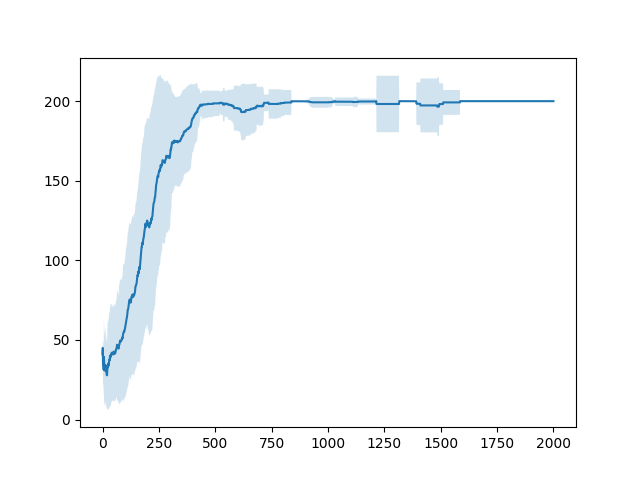
学習ができているか否か判定するにはこちらの方が直感的に分かりやすいことが分かる。
#参考文献
OpenAI Gym
CartPole-v0