どうも、自称人工社会プログラマのKeiです。
Pythonで人工社会シミュレーションの記事に思ったより沢山の研究者・大学院生らしき方々からいいねを頂けて、「マルチエージェントシミュレーション(MAS)って思ったよりやりたい人多いんだなー」と驚いています。
参考: https://www.slideshare.net/zansa/zansa
それはさておきMASを一度でもやったことがあり、かつC++のような速いけど書きにくい言語を避けてPythonのようなスクリプト言語を使っている方なら次のような悩みを一度は抱えたことありませんか?
「Python書きやすくて複雑なモデル組むのもラクなんだけど、やっぱり遅さが気になるんだよな...」
「ん、いや待てCythonなんていう手があるのか。でもなんか難しそうだし使いこなせるかな...」
はい、完全に自分です←
もちろんPythonはよくあるベクトル・行列演算などであればNumpyを使って効率よく計算できるのですが、ことMASに限って言えば大量の四則演算をゴリゴリやるというよりは、全エージェントが意思決定のために何千回何万回と乱数を振り、その結果をif文で細かく条件判定するような処理を繰り返すことが多く、よくあるPythonの高速化テクをなかなか適用しにくいという事情があります。
とは言っても、一度Pythonの書き味を味わってからまたあの不便なC系言語に戻れとか言われても嫌だというのが人情。
という訳で何かいい落とし所はないもんかといろいろ試した末に自分が辿り着いた結論があります。
それは最近話題のJuliaへの移行です。

Juliaは
- Pythonと非常によく似た書きやすい文法
- 数値計算用の豊富なライブラリ(Pythonライブラリも呼び出せる)
- 並列計算の容易さ
- JITコンパイラによるC言語並みの実行速度
を併せ持つという何とも凄まじい言語であり、Pythonの後継として注目を集めるのも納得なわけですが、まだまだユーザーが少なく日本語の文献も少ないという現状があります。とはいえ一度触れてみると、その書き味の良さと圧倒的な実行速度に自分はすっかり酔心してしまいました。
という訳で早速前回同様に囚人のジレンマゲームをJuliaで実装してみて、Pythonの時と比べ書き方にどのような違いがあるのか、またどれくらい高速化できるのかを比較してみたのが今回の記事になります。なおここではJuliaの文法の細かい解説までは行いません。そんなに高度なテクニックも使っていないので、ひとまずstructとfunctionの定義の仕方だけ抑えておいて貰えれば大抵理解できるレベルのコードだと思います。コード全体はGithub にも上げています。
また先に述べておきますが何もかもJuliaだけで済ませられた訳ではありませんでした。特にエージェント達の社会ネットワークの生成にはやはりPythonのNetworkXが手放せず、PyCallというライブラリを用いてJuliaからNetworkXを呼び出して使用しています。一応JuliaにもLightGraphsというNetworkXそっくりのライブラリがあったのですが、こちらは後述するように一部の関数でバグ(?)があったため、もうしばらくバージョンアップを待つことにします...
まずは人工社会の型を定義
はい、いきなりですが今回の実装では前回の記事における実装や一般的なMASのコードとは根本的に異なる点が1つあります。それはエージェント(オブジェクト)一体一体の捉え方です。通常MASと言えば一人のエージェントが持つ内部状態や戦略といった属性値を定義した以下のようなエージェントクラスを用意し、
# Pythonの場合
class Agent:
def __init__(self, state="active", point=0, strategy="tweet"):
self.state = state
self.point = point
self.strategy = strategy
それらを配列の中に詰め込んだ以下のようなものを人工社会として用いるのが定石です。
society = [Agent() for i in range(10000)]
この方法なら1人1人のエージェントがどこにいるのかが明確でコードがとても直感的に書けるので、今回Juliaで実装するときもまず始めはこの方法で実装し、実行時間を計測しました。そして判明したのですが、この方法は(少なくともJuliaで動かす限りは)非常に効率が悪いです。
そこでもう1つの考え方として、エージェント達の情報を以下のようなStructに格納してはどうかと考えました。
mutable struct SocietyType
state::Vector{AbstractString}
point::Vector{Float64}
strategy::Vector{AbstractString}
end
このようにするとi番目のエージェントの状態はstate, point, strategyという配列のi番目に格納された値を参照することで取得できます。
たったこれだけなのですが、実行時間を比較した所全計算時間が通常の6分の1程度 にまで圧縮されました。もしかして前回Pythonで実装してたコードもこの方法にしたら速くなるかも?と思い試してみたのですが、若干は速くなったもののJuliaの時ほど劇的な差はありませんでした。何なんでしょうねこの差はw
何はともあれJuliaではこちらの方が明らかに効率の良い実装だということはわかったので、このやり方で人工社会を表すStructを定義したものが以下になります。
module Society
export SocietyType
mutable struct SocietyType
population::Int # 全エージェントの人数
strategy::Vector{AbstractString} # 現在の戦略、VectorはPythonでいうリスト
next_strategy::Vector{AbstractString} # 次の戦略
point::Vector{Float64} # ゲームで獲得した利得
neighbors_id::Vector{Vector{Int}} # 全エージェントの隣人のID。ネストしたVectorになります。
# Juliaではコンストラクタはこのように定義します
# topologyにはPyCallで呼び出したNetworkXのグラフオブジェクトを代入します
SocietyType(population, topology) = new(population,
["D" for i = 1:population], # Pythonのリスト内包表記がJuliaにも取り入れられています
["D" for i = 1:population], # 最初は全員裏切り戦略で初期化
[0 for i = 1:population], # 全員0点で初期化
[[nb_id+1 for nb_id in topology[i]] for i = 1:population] # ここ注意
)
end
end
注意する点は上にもコメントしてあるようにneighbors_idに入れる値です。今回の実装だとエージェント同士を識別するためのIDはstrategy, pointなどの配列のインデックスです。そしてJuliaではPythonと異なり配列のインデックスは1始まりです。そのため内包表記を使ってneighbors_idを初期化する部分で普通に
[[nb_id for nb_id in topology[i]] for i = 1:population]
と書いてしまうと、topology[i]で返ってくる配列(ノード番号iとリンクを持つ全ノードのIDが入ったリスト)にはPython(NetworkX)で作ったグラフである以上当然ID: 0が含まれており、ID: 0のエージェントとリンクを持つエージェントが自分の隣人達の情報を参照する時に「Juliaの配列に0番目の要素なんてねーよ!」と怒られてしまいます(経験者は語る)。
あとはJuliaのStructだと各属性値に型の指定が要る点もPythonのクラス定義とは異なりますが、このくらいの手間ならCythonやNumbaの型指定と似たようなものなのでそんなに気になりませんね。
戦略適応に関する関数達
こちらに関しては前回Pythonで実装した内容と全く同じものをJuliaで書き直しただけですので、エージェントの定義の仕方が変わったことに対応して全エージェントに対するイテレーションの回し方が少し変わったくらいです。
強いて言うならJuliaでPythonのrandom.sampleに相当するような重複無しのランダムサンプリングを行う関数を見つけるのに少し苦労したのですが、StatsBase というライブラリにちょうど良いのが入っていました。
module Decision
export choose_initial_cooperators, initialize_strategy, count_payoff, pairwise_fermi, count_fc
using StatsBase
# 全人口からその半数を最初に協調(=C)戦略を持つエージェントとしてランダムサンプリングする(重複無し)
function choose_initial_cooperators(population)
init_c = StatsBase.self_avoid_sample!(1:population, [i for i = 1:Int(population/2)])
return init_c
end
# 全エージェントの戦略を初期化(C戦略:D戦略=50:50)
function initialize_strategy(society, init_c)
for id = 1:society.population
society.strategy[id] = ifelse(id in init_c, "C", "D")
end
end
# 全エージェントが獲得する利得を計算
function count_payoff(society, dg, dr)
R = 1 # Reward
T = 1+dg # Temptation
S = -dr # Sucker
P = 0 # Punishment
for id = 1:society.population
society.point[id] = 0
for nb_id in society.neighbors_id[id]
if society.strategy[id] == "C" && society.strategy[nb_id] == "C"
society.point[id] += R
elseif society.strategy[id] == "D" && society.strategy[nb_id] == "C"
society.point[id] += T
elseif society.strategy[id] == "C" && society.strategy[nb_id] == "D"
society.point[id] += S
elseif society.strategy[id] == "D" && society.strategy[nb_id] == "D"
society.point[id] += P
end
end
end
end
# Pairwise-Fermiモデルで全エージェントの戦略を更新
function pairwise_fermi(society)
for id = 1:society.population
opp_id = rand(society.neighbors_id[id]) # 自分の隣人達のIDからランダムに1つ選ぶ
society.next_strategy[id] = ifelse(rand() < 1/(1+exp((society.point[id] - society.point[opp_id])/0.1)), society.strategy[opp_id], society.strategy[id])
end
society.strategy = copy(society.next_strategy)
end
# C戦略を持つエージェントの割合を集計
function count_fc(society)
fc = length([1 for strategy in society.strategy if strategy == "C"])/society.population
return fc
end
end
ifelse関数がちょうどExcelのIF関数みたいな使い勝手で便利です。公式曰く普通にifとelseで書くより速いらしいです。
シミュレーション実行部
上で定義したSocietyTypeとDecisionモジュールの関数達を用いて前回同様にシミュレーションの流れを組み立てていきます。
エージェントたちの社会ネットワークを生成している部分についてはLightGraphs.barabasi_albertを使っても同じものを返してくれると思っていたのですが、これを使うとリンクを1本も持たないノード(つまり他のエージェント達と何の相互作用も起こさないエージェント)がわんさか生成されるということが判明したのでしぶしぶPyCallしてNetworkXに頼っています。この問題さえなければ全部Juliaで書けただけに残念。
include("society.jl")
include("decision.jl")
module Simulation
export run, one_episode
using ..Society
using ..Decision
using CSV
using DataFrames
# あるパラメータ設定の下でゲームを1000回行う。今回計測しているのはこの関数の実行時間。
function run(society, init_c, dg, dr)
initialize_strategy(society, init_c)
init_fc = count_fc(society)
println("Dg: $(dg), Dr: $(dr), Time: 0, Fc:$(init_fc)")
for step = 1:1000
count_payoff(society, dg, dr)
pairwise_fermi(society)
global fc = count_fc(society) # Juliaのfor文は新たな変数スコープを作るので、ここでglobalを付けないと最後にreturnする時にundefinedと怒られる
println("Dg: $(dg), Dr: $(dr), Time: $(step), Fc:$(fc)")
end
return fc
end
# 全パラメータ領域でrunを実行する
function one_episode(episode, population, topology)
society = SocietyType(population, topology)
DataFrame(Dg = [], Dr = [], Fc = []) |> CSV.write("result$(episode).csv") # 計算結果はこのファイルに書き込む
init_c = choose_initial_cooperators(population)
for dg = 0:0.1:1 # 社会ジレンマの強さを変えながらrunを何度も実行する
for dr = 0:0.1:1
fc = run(society, init_c, dg, dr)
DataFrame(Dg = [dg], Dr = [dr], Fc = [fc]) |> CSV.write("result$(episode).csv", append=true) # append=trueとすると上でヘッダーだけ書き込んだcsvファイルの行方向に追記していける
end
end
end
end
# ここからがメイン実行部
using .Simulation
using Random
using PyCall
@pyimport networkx as nx
const num_episode = 100 # アンサンブル平均を取るエピソード数
const population = 10000 # エージェントの人数
const topology = nx.barabasi_albert_graph(population, 4) # エージェントたちの社会ネットワーク。今回も平均次数8のスケールフリーネットワークを使用。
# 100エピソード分計算する
for episode = 1:num_episode
Random.seed!() # 毎エピソード乱数系列を初期化する
one_episode(episode, population, topology)
end
このコードを使い、特に重たいrunの部分の実行時間のベンチマークを取ったものが以下になります。なおJuliaでは@timeマクロを計測したい処理の頭に付けてコードを実行するだけで実行時間が測れます。
比較のために素のPythonとCythonで上に書いたコードと同じものを実行した際の計算時間を並べてみました。
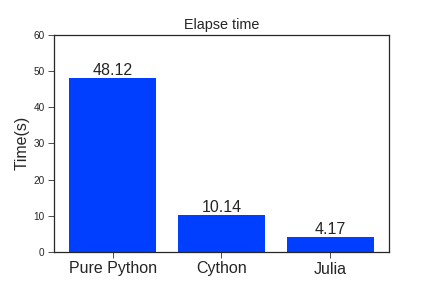
(いずれもDg=Dr=0.1と設定した際にrunに相当する処理を実行)
...たった4秒 !??? Pythonで50秒近くかかってたのに!!!!
そりゃ素のPythonと比較して速くなるのが当然なのは分かっていますが、Cythonと比較してもなおJuliaの方が2倍以上速いという結果になるとは正直予想外でした。まあCython歴の浅い自分が実装したコードなのでそこまで上手く高速化出来ていない可能性もありますが、それでも普通のPythonと同じように(struct部分を除き)何の型宣言も無しでこの速度が出るなら初心者が下手にCythonに手を出すより最初からJuliaで書いたほうが明らかに良いですね。
という訳で、人文系・理工系問わずマルチエージェントシミュレーションに取り組む皆様、上のJuliaのコードを見てそんなに抵抗感を感じなければ、そろそろそろPythonからJuliaに移行して圧倒的な計算スピードを謳歌してみてはいかがでしょうか?