Pythonで人工社会シミュレーション

Keiです。突然ですが、みなさんマルチエージェントシミュレーション(エージェントベースモデリング) ってご存知ですか？

マルチエージェントシミュレーション(よくMASと略されます)とは人間のように内部状態や行動ルールを持ち、自律的に意思決定を行う｢エージェント｣と呼ばれるオブジェクトを多数用いて仮想的な社会を作り、それらを用いて現実の様々な事象をモデル化しようというものです。タイトルにもあるように**「人工社会シミュレーション」**と呼ばれることもあります。

MASがどういう現象の分析で力を発揮するかというと、

1. 注目している現象が複雑で簡単な微分方程式ではシステムの振る舞いを上手く説明できない時
   => 金融市場でのディーラーの振る舞い、Twitter上でのリツイートの伝播など
2. 人々の意思決定に社会ジレンマが存在する時
   => 自分の利益だけ考えるとA戦略が良いけど社会全体のためにはB戦略をとるのが良いみたいな
3. ネットワークで結ばれたもの(人・車・微生物など)同士が相互作用し合う時
   => 噂の広めあい、インフルエンザの伝染など

などです。やり方次第で(十分な計算資源さえあれば)どれだけ複雑な現象であってもシミュレーション可能で、一部の企業ではマーケティングシミュレーションなんかに既に利用されています(興味のある方はマルチエージェントのためのデータ解析とか読んでもらえると)。

そんな便利なMASですが、僕自身大学院に入って最初に先生に言い渡されたMASの課題に取り組もうと思った時にあまり手頃な実装例が見つからずそれなりに苦しんだ覚えがあるので、今回はまず簡単な計算を題材にMASの実装例を紹介していこうと思います。

全体のコードはGithubに載せています。以下に載せているコードは囚人のジレンマゲームのシミュレーションを行うために必要な最低限の部分のみに絞っているため(もちろんこれだけで動きますが)、完全なコードを見たい方はGithubの方を見てください。

シミュレーションモデル

MASを使った進化計算の中で最も基礎的な(それでいて未だに日進月歩のペースで研究が進んでいる)例に囚人のジレンマゲームというものがあるのですが、今回はこれをネットワークで結ばれた1万人のエージェント達で構成される人工社会の中で繰り広げてみることにします。
囚人のジレンマゲームでやっている事は非常にシンプルで、コンピュータ上に生成した無数のエージェント達それぞれに、周囲の隣人エージェントに対して協力する(C戦略)か裏切る(D戦略)かどちらか1つの戦略を選ばせる、ということをひたすら繰り返させるだけです。エージェント達は毎回のゲームでデタラメに戦略を決定しているのではなく、選んだ戦略に応じて得られる"利得(Payoff)"が高い周囲のエージェントの戦略を次のゲームで高確率で真似するようにします。これによってゲーム理論が前提とする"合理的な意思決定"を表現しているわけですね。
ちなみにゲーム理論や囚人のジレンマについてはこちらのサイトに非常に分かりやすくまとまっているので興味のある方はぜひ。

エージェントクラスを用意

まずはマルチエージェントシステムの核となるエージェントクラスを定義しておきます。
エージェントは1人1人が

• 戦略(C or D)
• 次のゲームでの戦略(C or D)
• ゲームで獲得した利得
• ネットワークで結ばれた隣人エージェントのID

を保持し、後述するPairwise-Fermiモデルに基づいて自律的に意思決定を行い毎回のゲームで出す戦略を決定します。

agent.py

import random as rnd
import numpy as np

class Agent:
    def __init__(self):
        self.point = 0.0
        self.strategy = None
        self.next_strategy = None
        self.neighbors_id = []

    def decide_next_strategy(self, agents):
        """Pairwise-Fermiモデルで次のゲームでの戦略を決定する"""

        opponent_id = rnd.choice(self.neighbors_id)  # 戦略決定時に参照する隣人エージェントをランダムに選ぶ
        opponent = agents[opponent_id]

        if opponent.strategy != self.strategy and rnd.random() < 1/(1 + np.exp((self.point - opponent.point)/0.1)):
            self.next_strategy = opponent.strategy
        
    def update_strategy(self):
        self.strategy = self.next_strategy

Pairwise-Fermiモデルとは何ぞや?

エージェントがどういう判断基準に基づいて戦略を変更するのかについてはまだ「絶対このやり方が正しい!」みたいなものは学術界にも存在していないのですが、今回はひとまず進化ゲームの研究で最も広く用いられているPairwise-Fermi Comparisonというモデルを採用しています。
このモデルでは各エージェント達が知人関係を表すネットワーク上で結ばれた隣人の中からランダムに一人を選び、選ばれた対戦相手が自分より高い利得を稼いでいればいるほどより高い確率でその戦略を真似するというものです。念のため数式も書いておきます。

  p_{i\leftarrow\ j} = \frac{1}{1+exp(\frac{\pi_{i}-\pi_{j}}{\kappa})}

この式はエージェントiがエージェントjの戦略を真似する確率を定義していて、πというのはそれぞれのエージェントがゲームの結果獲得した利得です。$\kappa$は温度係数と呼ばれるパラメータで、エージェント達が対戦相手との得点差に対してどれくらい敏感に戦略を変更するのかを決めています。ここでもkappaの値は進化ゲームの研究で広く持ちいられている0.1という値を採用することにします。

シミュレーションクラスを用意

シミュレーションの流れは

1. パラメータ設定(ジレンマ強さ)を更新
2. エージェント達の戦略の初期化(これが最初のゲーム)
3. ゲームで獲得した利得の計算
4. 次のゲームの戦略を決定
5. 戦略比を集計し、値が一定値に収束するまで3→4を繰り返す
6. 全パラメータ領域での計算が終わるまで1〜5を繰り返す。
   のようになっており、以下特に2〜4の部分を重点的に説明していきます。

コンストラクタ

コンストラクタは以下の通りで、全エージェントの生成と初期のC戦略エージェントの番号を用意しています。注意がいる点としては初期C戦略エージェントの番号は1.でパラメータ設定を変更しても同じものを使い回す必要があり、最初にインスタンス変数にセットしてキープしておかなければならない事です。

simulation.py

import numpy as np
import random as rnd
import networkx as nx
import pandas as pd
from agent import Agent

class Simulation:
    def __init__(self, population, average_degree):
        self.agents = self.__generate_agents(population, average_degree)
        self.initial_cooperators = self.__choose_initial_cooperators() 

    def __generate_agents(self, population, average_degree):
        """エージェントをリストに詰め、隣人エージェントのIDをセットする"""

        rearange_edges = average_degree//2
        network = nx.barabasi_albert_graph(population, rearange_edges)

        agents = [Agent() for id in range(population)]
        for index, focal in enumerate(agents):
            neighbors_id = list(network[index])  # list()無しだとgeneratorになってしまうので注意
            for agent_id in neighbors_id:
                focal.neighbors_id.append(agent_id)
        
        return agents

     def __choose_initial_cooperators(self):
        """最初のゲームでC戦略を取るエージェントをランダムに選ぶ"""

        population = len(self.agents)
        initial_cooperators = rnd.sample(range(population), k = int(population/2))

        return initial_cooperators

generate_agentsメソッドの中ではネットワーク上の進化ゲームのシミュレーションでは定番のNetworkXを使うことで、社会ネットワークの生成から任意のエージェントの隣人エージェントのノード番号の取得までを超手短かに記述できています。
また今回ネットワーク構造にはTwitter等のSNSで似たような構造が見られることで有名なBarabashi-Albert Scale Free Networkを用いています。このネットワークは自力で実装しようとするとそれなりに面倒なのですが、NetworkXならたった一行で実装できてしまいます。正直MASをPythonで実装するメリットのほとんどはNetworkXが使える点に尽きます。

戦略の初期化に使うメソッド

エージェント達の戦略の初期化に使うメソッドを以下のように定義します。コンストラクタで決定しておいた初期C戦略エージェントの番号を持つエージェントにC戦略, それ以外のエージェントにD戦略を割り当てます。なお最初のゲームではC戦略とD戦略を取るエージェントの人数比は1:1にしておきます。

simulation.py

    # Simulationクラスの続き
    def __initialize_strategy(self):
        """全エージェントの戦略を初期化"""

        for index, focal in enumerate(self.agents):
            if index in self.initial_cooperators:
                focal.strategy = "C"
            else:
                focal.strategy = "D"

ちなみに上のコードで出てくるfocalというのは"focal agent"の略で、進化ゲーム界隈では戦略更新の最中などで注目しているエージェントを指してfocalと呼び、隣人エージェントや戦略を模倣する相手と区別する事が多いのでこのような変数名をつけています。

ゲームで獲得した利得の計算

毎回のゲームでエージェント達が獲得する利得というポイントを以下の表(利得行列)のように定義しておき、戦略に応じて全エージェントに利得を与えます。表の見方としては、例えば自分も相手もC戦略なら自分は1点獲得、といった感じです。

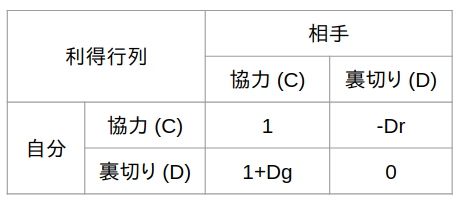
囚人のジレンマゲームでは1回のゲームで獲得できる得点は社会におけるジレンマ強さDgとDr(チキン型ジレンマの強さとスタグハント型ジレンマの強さと言います)の値によって変わるので、以下に定義するcount_payoff関数では引数にDgとDrを渡しています。なお R(Reward), S(Sucker), T(Temptation), P(Punishment)という4種類の得点の名前は進化ゲーム理論で用いられる専門用語で、ジレンマゲームの研究ではこれらの得点の大小関係をどう変えると理想とする社会を作り出せるか、という所に関心があります。

また余談ですが、各エージェントは隣人全員とゲームして得た得点を合計するようになっていて、今回の計算ではネットワーク構造にBA-SFネットワークを採用している関係で、ごく少数存在するものすごく大勢の人と繋がりがあるエージェント(SNS上でのインフルエンサーみたいなエージェント。ハブと言います)が隣人の数だけゲームして大量の得点を稼いでくるので、ハブエージェントの戦略は周囲の隣人エージェント達から非常に真似されやすくなります。インフルエンサーの影響力はリアルだけじゃなく人工社会でも絶大だった。。。

simulation.py

    def __count_payoff(self, Dg, Dr):
        """利得表に基づいて全エージェントが獲得する利得を計算"""

        R = 1       # Reward
        S = -Dr     # Sucker
        T = 1+Dg    # Temptation
        P = 0       # Punishment

        for focal in self.agents:
            focal.point = 0.0
            for nb_id in focal.neighbors_id:
                neighbor = self.agents[nb_id]
                if focal.strategy == "C" and neighbor.strategy == "C":    
                    focal.point += R 
                elif focal.strategy == "C" and neighbor.strategy == "D":   
                    focal.point += S
                elif focal.strategy == "D" and neighbor.strategy == "C":   
                    focal.point += T
                elif focal.strategy == "D" and neighbor.strategy == "D":  
                    focal.point += P

次のゲームの戦略を決定

ここは見たまんまなので特に説明は要らないでしょう。全エージェントにdecide_next_strategyとupdate_strategyを実行させるだけです。

simulation.py

    def __update_strategy(self):
        """全エージェントに戦略を更新させる"""

        for focal in self.agents:
            focal.decide_next_strategy(self.agents)
        
        for focal in self.agents:
            focal.update_strategy()

戦略比の集計

毎タイムステップ全エージェントの得点計算と戦略更新が終わる度に、社会全体に占めるC戦略エージェントの割合(=協調率)を集計してそのダイナミクスを見ることにします。協調率は基本的に計算開始後一旦大きく下がり、その後持ち直してきて、社会ジレンマ(DgとDr)の弱い世界ではそのまま全員が協力エージェントに、ジレンマでガチガチの世界では持ち直しが効かずに全員が裏切り合いを永遠に続ける様子を観察出来ます。

以下では内包表記を使い、C戦略を持つエージェントだけを抽出して作られたリストの長さを全エージェントの人数で割って協調率を出しています。普通にfor文とif文でカウントしたりfilter関数使っても良いんですが、エージェントの人数が1万人くらいまで増えると明らかに内包表記使った方が速くなります。

simulation.py

    def __count_fc(self):
        """C戦略エージェントの割合を計算"""

        fc = len([agent for agent in self.agents if agent.strategy == "C"])/len(self.agents)

        return fc

シミュレーションフローの定義

ここまでで必要な部品は揃ったので、最初に説明した順番の通りに各メソッドを並べていきます。play_gameで一つのパラメータ設定において協調率が収束するまでの計算を行い、それをrun_one_episode内でパラメータ設定を変えて何度も呼び出しています。

simulation.py

    def __play_game(self, episode, Dg, Dr):
        """一つのパラメータ設定で協調率が収束するまで計算"""

        self.__initialize_strategy()
        initial_fc = self.__count_fc()
        fc_hist = [initial_fc]
        print(f"Episode:{episode}, Dr:{Dr:.1f}, Dg:{Dg:.1f}, Time: 0, Fc:{initial_fc:.3f}")

        tmax = 3000
        for t in range(tmax):
            self.__count_payoff(Dg, Dr)
            self.__update_strategy()
            fc = self.__count_fc()
            fc_hist.append(fc)
            print(f"Episode:{episode}, Dr:{Dr:.1f}, Dg:{Dg:.1f}, Time:{t}, Fc:{fc:.3f}")

            ##### 収束判定 #####
            # 100回以上戦略更新を繰り返し、過去100回のゲームで得られた協調率の平均値と次のゲームでの協調率の差が十分小さくなったら計算を打ち切る
            if (t >= 100 and np.absolute(np.mean(fc_hist[t-100:t-1]) - fc)/fc < 0.001) or t == tmax-1:
                fc_converged = np.mean(fc_hist[t-99:t])  # 過去100回分のゲームで得られた協調率の平均値を取る
                break

            # 囚人のジレンマゲームでは全員C戦略 or 全員D戦略の状態に収束しやすいため、そうなったらすぐに計算を打ち切る
            elif fc in [0, 1.0]:
                fc_converged = fc
                break

        print(f"Dr:{Dr:.1f}, Dg:{Dg:.1f}, Time:{t}, Fc:{fc_converged:.3f}")

        return fc_converged

    def run_one_episode(self, episode):
        """全パラメータ領域でplay_gameを実行し、計算結果をCSVに書き出す"""

        result = pd.DataFrame({'Dg': [], 'Dr': [], 'Fc': []})
        self.__choose_initial_cooperators()

        for Dr in np.arange(0, 1.1, 0.1):
            for Dg in np.arange(0, 1.1, 0.1):
                fc_converged = self.__play_game(episode, Dg, Dr)
                new_result = pd.DataFrame([[format(Dg, '.1f'), format(Dr, '.1f'), fc_converged]], columns = ['Dg', 'Dr', 'Fc'])
                result = result.append(new_result)
        
        result.to_csv(f"episode{episode}.csv")

ドライバスクリプトを用意

あとはシミュレーション時のパラメータを定めたドライバスクリプトを使って計算を実行するだけです。なお実際の進化ゲームの研究などでは乱数系列によってシミュレーション結果が大きく変わることがあり得るため、同じ計算を100回くらい実行して全エピソードにおける計算結果のアンサンブル平均をとるということをやるのですが、今回はお試し計算なので計算回数は1回に設定しています。

main.py

from simulation import Simulation
import random

def run():
    population = 10000          # エージェント数
    average_degree = 8          # 社会ネットワークの平均次数
    num_episode = 1             # シミュレーションの試行回数
    simulation = Simulation(population, average_degree)

    for episode in range(num_episode):
        random.seed()
        simulation.run_one_episode(episode)

if __name__ == '__main__':
    run()

これで完成になります。あとはターミナルで

$ python main.py

した後に計算結果が吐き出されるのを待ってもらい、計算が終わったらPandasとSeabornでいい感じのヒートマップを描きましょう。(PandasとSeabornによる可視化の方法も次の記事で書きます)。
ジレンマ強さの異なる121種類の世界が進化を続けた結果、それぞれの世界で最終的に何割のエージェントが利他的な行動を取ることを選択するのかをあたかも神様にでもなったかのような目線で見ることが出来ます。

これであなたも人工社会シミュレーションの虜に...（＊˘︶˘＊）．｡．：＊♡

長くなりましたが、最後まで読んで頂きありがとうございます。Twitterの方でもよくプログラミングと進化ゲームのことつぶやいてるので、良かったらフォローお願いします!

<おまけ> 協調率をヒートマップで可視化した例

BA-SF ネットワーク	正方格子

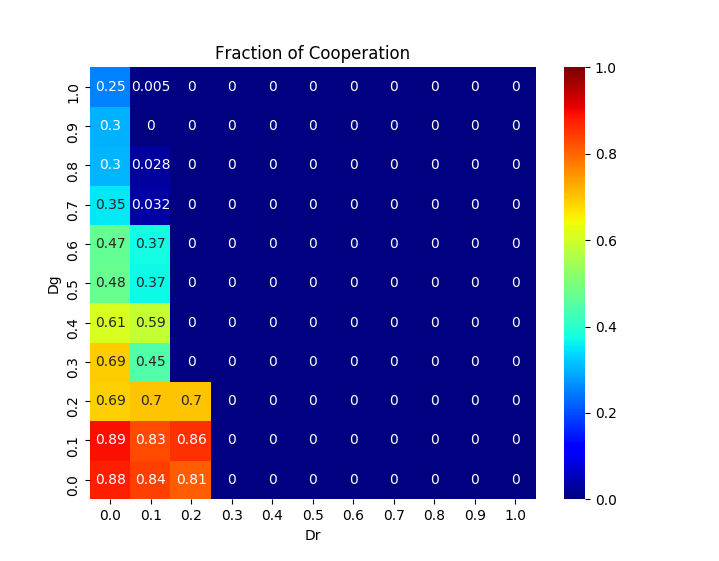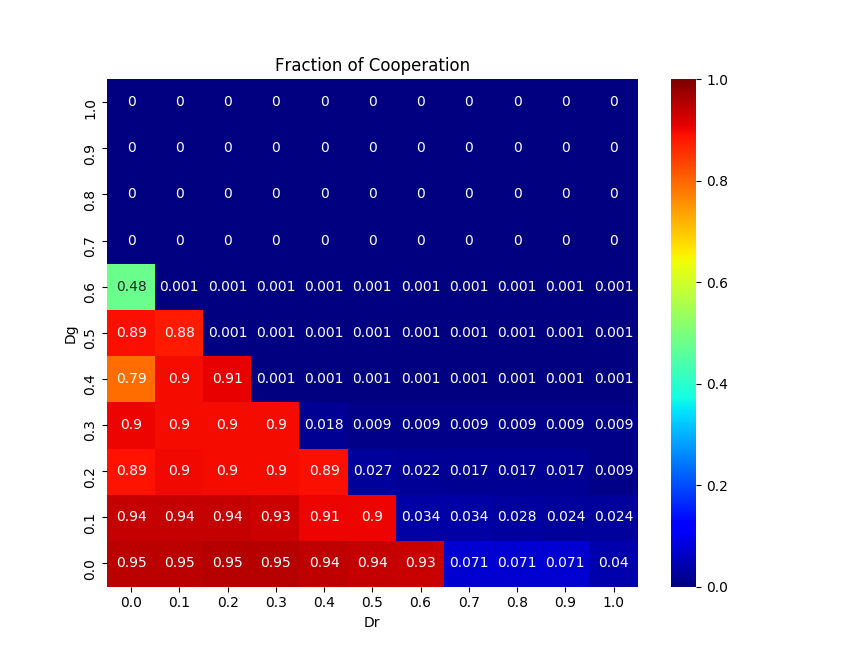エージェントたちの戦略が進化していく様子

協調者のテリトリーが拡大していく様子が分かりやすいようBA-SFネットワークではなく正方格子状のネットワーク構造を仮定し(簡単そうに見えて実は正方格子の方が実装がややこしいので上ではあえてスケールフリーネットワークを使いました)、Pairwise Fermiモデルを使って計算した時の社会が進化していく様子をgifアニメにしてみました。協力戦略を取る人達がじわじわと勢力を拡大していっている様子がよく分かります。

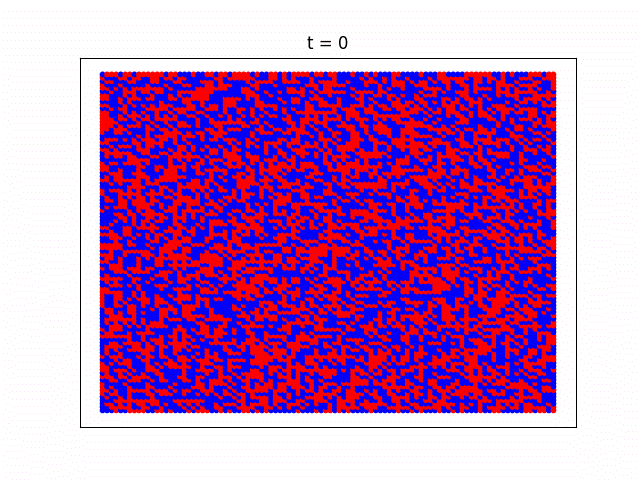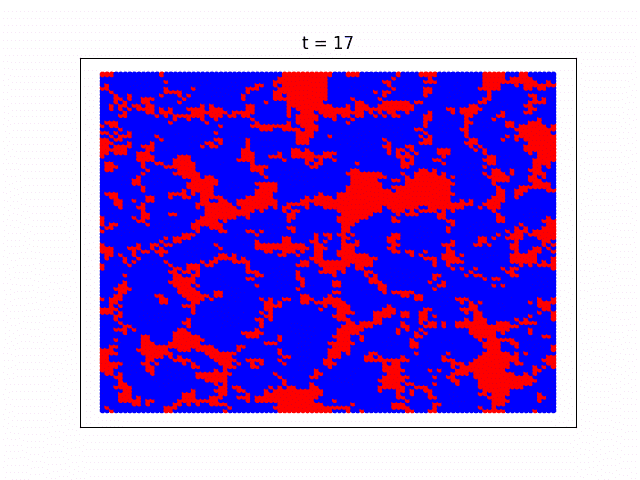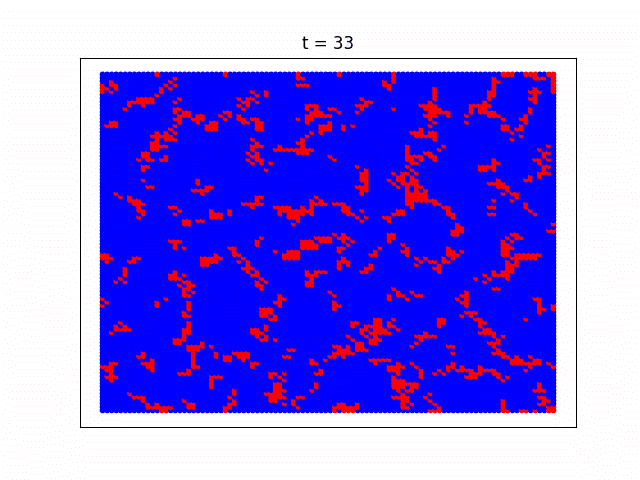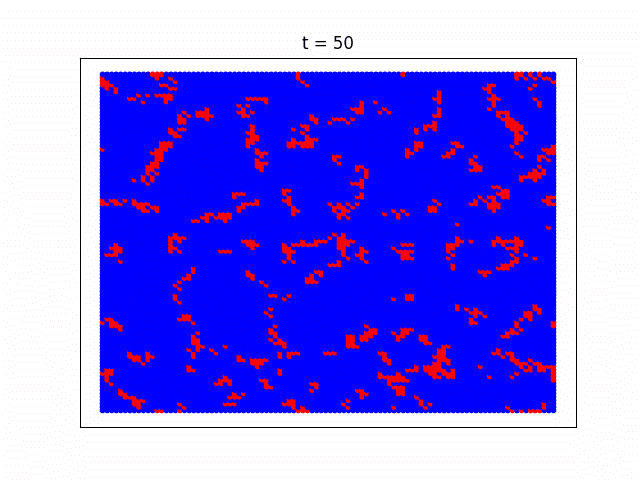
青い部分が協力戦略をとっているエージェント、赤が裏切り者達です。一番最初のゲームの時には協力エージェントと裏切りエージェントはそれぞれ5000人ずつランダムに配置していて、最初は裏切り者たちが徐々に社会を埋め尽くしていきますが、運良く生き残った協力エージェントたちが次第に群れ(=クラスター)を成して裏切り者達の侵攻を防ぎ、最終的には協力エージェントが社会の多数派を占めていく様子が見れます。