こんにちは、Keiです。
前回はPythonで人工社会シミュレーションというテーマで書きましたが、今回はそれの実社会への応用としてマルチエージェントシステムとゲーム理論を用いた感染症のシミュレーションに挑戦したいと思います。要は人工社会上でインフルエンザみたいな病気をぶちまけたらどうなるかを見守ろうという魂胆です。そういえば最近丁度そんなスマホゲームが流行ってましたよね。


実はこのような感染症のシミュレーションは「SIRモデル」と呼ばれるもので、感染アルゴリズムをちょこっと変えるだけで噂や情報の伝播の様子をモデル化できたりするので、最近はTwitterでバズったツイートがどういうメカニズムでRTの波にのってネット上を駆け巡るのか、またどうやったらツイートを効率よく拡散させられるのかなどをこのモデルで調べている人達もいるそうです。
ところで、感染症と言えば当然流行って欲しくないものの筆頭です。そして感染症の流行を抑えるのに最も効果的な手段は人々に前もってワクチン・予防接種等を行ってもらうことです。そこで今回はこのSIRモデルによる通常の感染症シミュレーションに少し手を加え、感染症の流行前にエージェント達がワクチンを打つかどうかの意思決定を行うようにして、より現実的なシミュレーションを行ってみたいと思います。意思決定の部分には例に習ってゲーム理論を用います。以下順番に説明していきます。
エージェントの定義
まずは前回同様エージェントを定義し、知人関係のネットワークで結ばれたエージェント達を多数生成するための関数を用意しておきます。なお今回エージェントには
- 健康状態 (S, IM, I, R の4状態をとる)
- 戦略 (V, NVの2戦略がある)
- 利得 (point)
- 隣人エージェントのID
を属性として持たせます。知人関係のネットワークの生成にはnetworkXを使います。ネットワークの種類は何でも良いのですが、今回も前回に引き続きバラバシ・アルバート スケールフリーネットワークを使用しました。このネットワークはSNSやインターネットを始め現実の至るところで見られる非常に有名なグラフで、特に性感染症の伝播と関係の深い男女関係などもこのネットワークに近いものになっています。
import networkx as nx
class Agent:
def __init__(self):
"""
state = ['S', 'IM', 'I', 'R'] (S: Susceptible, IM: Immuned, I: Infectious, R: Recovered)
strategy = ['V', 'NV'] (V: Vaccinator, NV: Non-vaccinator)
"""
self.state = 'S'
self.strategy = 'V'
self.next_strategy = 'V'
self.point = 0
self.neighbors_id = None
def generate_agents(num_agent, average_degree):
network = nx.barabasi_albert_graph(num_agent, average_degree//2)
agents = [Agent() for agent_id in range(num_agent)]
for agent_id, agent in enumerate(agents):
agent.neighbors_id = list(network[agent_id])
return agents
def count_state_fraction(agents):
"""Count the fraction of S/IM/I/R state agents"""
fs = len([agent for agent in agents if agent.state =='S'])/len(agents)
fim = len([agent for agent in agents if agent.state =='IM'])/len(agents)
fi = len([agent for agent in agents if agent.state =='I'])/len(agents)
fr = 1 - fs - fim - fi
return fs, fim, fi, fr
def count_num_i(agents):
"""Count the number of infected agents"""
num_i = len([agent for agent in agents if agent.state == 'I'])
return num_i
def count_fv(agents):
"""Count the fraction of vaccinators"""
fv = len([agent for agent in agents if agent.strategy == 'V'])/len(agents)
return fv
def count_num_nv(agents):
"""Count the number of non-vaccinators"""
num_nv = len([agent for agent in agents if agent.strategy == 'NV'])
return num_nv
def count_sap(agents):
sap = np.mean([agent.point for agent in agents])
return sap
感染ダイナミクス
次に感染症の伝播の様子を規定する関数達を定義していきます。
条件分岐が多いですがやっていることはそんなに難しくなくて、以下に示すdisease_spreading関数の中で
- 自分はまだ健康(S状態) → 隣人の中に感染者(I状態)がいたら、感染者数に比例する確率で自分も感染してI状態に遷移。感染者一人との接触による感染確率はβという値で設定しています。
- 自分は健康状態でかつワクチンを打っている → そのワクチンがちゃんと効いていれば(Immuned状態になっていれば)感染しない。もし運悪くワクチンが効いていなかったら(S状態なら)ワクチンを打っていない人同様の手順で感染。ワクチンが有効である確率はeffectivenessという値で定めています。
- 自分は既に感染していて回復待ち → 回復確率(gamma)に応じて病気から回復(R状態へ)
- 自分は既に病気にかかった上で免疫を獲得している(R状態) → 何も起こらない。
というアルゴリズムを実装しているだけです。またシーズンの最初の感染源となる人間はワクチン非接種戦略のエージェントの中から5人選ばれることにし、感染状態のエージェントが居なくなるまで全エージェントの状態の遷移を繰り返します。
import random as rnd
import society
def initialize_state(agents, Cr, effectiveness, num_initial_infected_agents=5):
"""
Randomely select initially infected agents from non-vaccinators and
determine the agents who get perfect immunity from vaccinators
"""
non_vaccinators_id = [agent_id for agent_id, agent in enumerate(agents) if agent.strategy == 'NV']
initial_infected_agent_id = rnd.sample(non_vaccinators_id, k = num_initial_infected_agents)
for i, agent in enumerate(agents):
if i in initial_infected_agent_id:
agent.state = 'I'
agent.point = -1
elif agent.strategy == 'V':
agent.point = -Cr
if rnd.random() <= effectiveness:
agent.state = 'IM'
else:
agent.state = 'S'
else:
agent.state = 'S'
agent.point = 0
def disease_spreading(agents, beta, gamma):
"""Calculate SIR dynamics until I agents disappear"""
for day in range(1, 100000):
# Only S or I state agents change their state, IM or R don't change their state!
state_changeable_agents = [agent for agent in agents if agent.state in ['S', 'I']]
next_states = ['S' for i in range(len(state_changeable_agants))]
for i, agent in enumerate(state_changeable_agents):
if agent.state == 'S':
num_infected_neighbors = len([agents[agent_id] for agent_id in agent.neighbors_id if agents[agent_id].state == 'I'])
if rnd.random() <= beta*num_infected_neighbors:
next_states[i] = 'I'
agent.point -= 1
else:
pass
elif agent.state == 'I':
if rnd.random() <= gamma:
next_states[i] = 'R'
else:
next_states[i] = 'I'
# Update state
for agent, next_state in zip(state_changeable_agents, next_states):
agent.state = next_state
fs, fim, fi, fr = society.count_state_fraction(agents)
num_i = society.count_num_i(state_changeable_agents)
print(f'Day: {day}, Fs: {fs:.2f}, Fim: {fim:.2f}, Fi: {fi:.2f}, Fr: {fr:.2f}')
if num_i == 0:
print('Disease spreading finished!')
break
return fs, fim, fi, fr
ワクチンを打つかどうかの意思決定
Epidemics.pyのinitialize_state関数とdisease_spreading関数は途中でエージェント達の利得(point)を計算していますが、これは毎シーズン初めにエージェント達がワクチンを打つかどうかの意思決定を行う際に参照する重要な値で、今回のモデルでは自分がワクチンを打ったかどうか、またその結果病気にかかったかどうかによって獲得する利得を次表のように定めています。このような利得の獲得の仕方をまとめた表はゲーム理論で利得行列と呼ばれます。
| 戦略\健康状態 | 健康 | 感染 |
|---|---|---|
| ワクチン接種 | -Cr | -Cr-1 |
| 非接種 | 0 | -1 |
上の利得行列においてCrはワクチン接種コストと呼ばれる値で、0から1の値を取ります。
見てもらえば分かるように一番高い利得を得られる組み合わせはワクチンを打たずに何とか感染を免れて健康でいるパターン(いわゆるナッシュ均衡に当てはまる)ですので、エージェント達が単に自分1人で意思決定を行う場合はワクチンを打たない戦略が最適戦略ということになります。
ですが感染症の伝播を伴う今回のような状況では意思決定はそんなに単純なものではありません。いつもいつも上手いこと感染を免れられるとは限らないからです。例えワクチン接種コストを支払ってでも、病気にかかって利得を1失うよりワクチンを打って免疫を獲得する方が感染を避けられる可能性が上がり、結果としてより高い利得を維持できるという状況も大いに有り得ます。こればかりは実際にシミュレーションしてみないと最終的に社会全体で何割の人がワクチンを打つことを選ぶのかは分からないのです。
そこで次のような手順で十分に進化した社会におけるワクチン接種者の割合とその時の感染者の割合を求めていくことにします。
- 最初の感染シーズンが始まる前に全エージェントの半分にワクチンを打たせておき、感染ダイナミクスを計算。
- 感染者が居なくなったら感染シーズンが収束したとみなし、次のシーズンでワクチンを打つかどうかを全エージェントに決めさせる。
- 2でワクチンを打つと決めた人にワクチンを打たせ、再度感染ダイナミクスを計算。
- ワクチン接種者の割合に変化がなくなるまで 2 ➔ 3の流れを繰り返す
イメージ的にはこんな感じ↓。
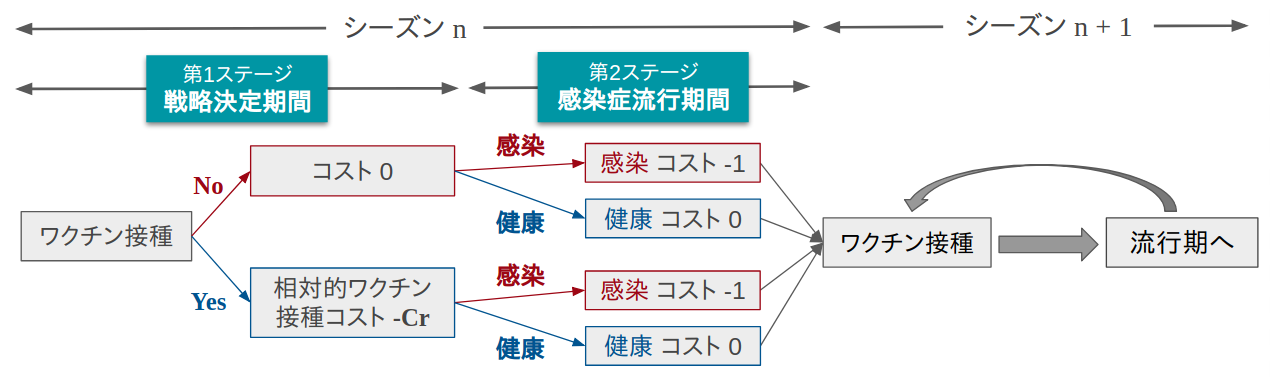
また戦略決定には下図に示すPairwise-Fermi比較と呼ばれる利得比較方法を用います。

以下が戦略決定にまつわる関数達の実装例です。
import numpy as np
import random as rnd
def choose_initial_vaccinators(num_agent):
"""Return agent id list which used for one episode"""
initial_vaccinators_id = rnd.sample(range(num_agent), k = num_agent//2)
return initial_vaccinators_id
def initialize_strategy(agents, initial_vaccinators_id):
"""Initialize the strategy of all agent with the given initial_vaccinators_id"""
for i, agent in enumerate(agents):
if i in initial_vaccinators_id:
agent.strategy = 'V'
else:
agent.strategy = 'NV'
def PW_Fermi(agents):
"""Determine next_strategy of all agents for the next season"""
kappa = 0.1 # Thermal coefficient
next_strategies = [agent.strategy for agent in agents]
# Randomely select one neighboring agent as opponent and determine whether or not copying his strategy
for i, focal in enumerate(agents):
opponent_id = rnd.choice(focal.neighbors_id)
opponent = agents[opponent_id]
if opponent.strategy != focal.strategy and rnd.random() <= 1/(1+np.exp((focal.point-opponent.point)/kappa)):
next_strategies[i] = opponent.strategy
else:
pass
# Update strategy
for agent, next_strategy in zip(agents, next_strategies):
agent.strategy = next_strategy
メイン関数
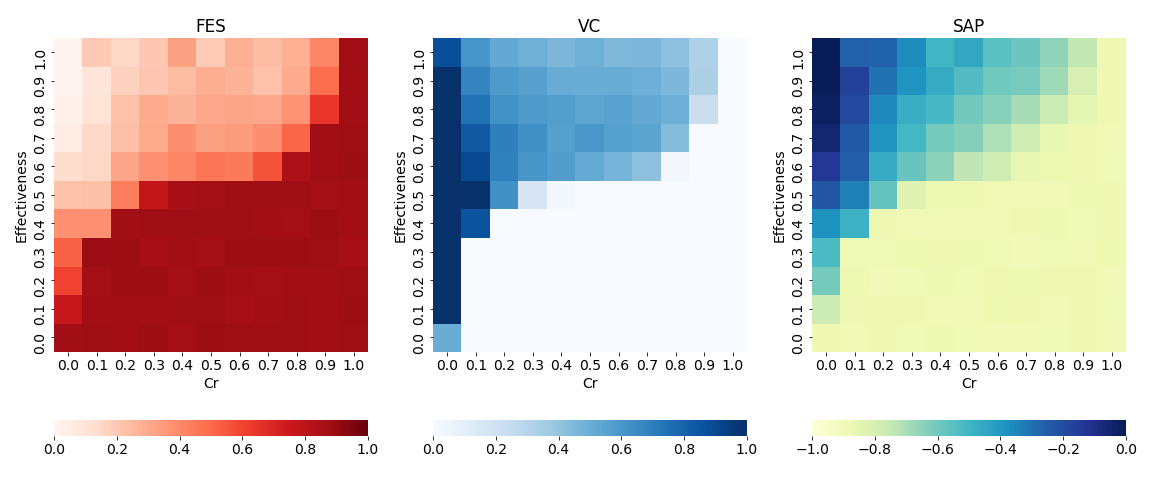
ここまでで計算に必要な部品は揃ったので、後は先程説明したシミュレーションフローに従って計算を実行していきます。ただしワクチン接種コストCrやワクチンが実際に効く確率を表すeffectivenessの値についてはいくつに設定するのが良いという確固たる指標が無いため、2つとも0〜1の範囲内で変化させて色々な条件で計算した結果を相図のようにまとめていくことにします。計算結果として見ていくのは
- 感染者の割合(FES: Final Epidemic Size)
- ワクチン接種者の割合(VC: Vaccination Coverage)
- 全エージェントの獲得した利得の平均値(SAP: Social Average Payoff)
の3つです。
計算の打ち切り条件の部分だけ少しややこしいので日本語でもコメントしています。
import numpy as np
import pandas as pd
import random as rnd
import society
import decision
import epidemics
def main():
### Calcualtion setting ###
num_agent = 10000 # Number of agent
average_degree = 8 # average degree of the social network
beta = 0.14 # Infection probability
gamma = 0.33 # Recovery probability
params_range = np.arange(0, 1.1, 0.1)
max_season = 1000
num_initial_infected_agents = 5
# Prepare agents & DataFrame to store result
agents = society.generate_agents(num_agent, average_degree)
result = pd.DataFrame({'Cr': [],
'Effectiveness': [],
'FES': [],
'VC': [],
'SAP': []
})
# Initialization of random seed and initial vaccinators
rnd.seed()
initial_vaccinators_id = decision.choose_initial_vaccinators(num_agent)
for Cr in params_range:
for effectiveness in params_range:
decision.initialize_strategy(agents, initial_vaccinators_id)
initial_fv = society.count_strategy_fraction(agents)
fv_hist = [initial_fv]
fes_hist = []
sap_hist = []
for season in range(1, max_season+1):
print(f'Cr: {Cr:.1f}, Effectiveness: {effectiveness:.1f}, Season: {season} starts...')
epidemics.initialize_state(agents, Cr, effectiveness)
fs, fim, fi, fr = epidemics.disease_spreading(agents, beta, gamma)
decision.PW_Fermi(agents)
fv = society.count_fv(agents)
num_nv = society.count_num_nv(agents)
sap = society.count_sap(agents)
fes_hist.append(fr)
fv_hist.append(fv)
sap_hist.append(sap)
# ワクチン接種者が増えすぎると初期感染者を選べなくなるのでそこで計算を打ち切る
if num_nv <= num_initial_infected_agents:
fes_eq = fr
fv_eq = fv_hist[-2] # fv_hist[-1]だと計算を打ち切ったシーズンの次のシーズンにおけるワクチン接種率になってしまうので
sap_eq = sap
break
elif (season >= 150 and np.mean(fv_hist[season-100:season-1]) - fv <= 0.001) or season == max_season:
fes_eq = np.mean(fes_hist[season-100:season-1])
fv_eq = np.mean(fv_hist[season-99:season]) # fv_histだけは他2つより要素数が1つ多いので平均を取る範囲が異なる
sap_eq = np.mean(sap_hist[season-100:season-1])
break
new_result = pd.DataFrame([[format(Cr, '.1f'), format(effectiveness, '.1f'), fes_eq, fv_eq, sap_eq]], columns = ['Cr', 'Effectiveness', 'FES', 'VC', 'SAP'])
result = result.append(new_result)
print(f'Cr: {Cr:.1f}, Effectiveness: {effectiveness:.1f}, Season finished with FES: {fes_eq:.2f}, VC: {fv_eq:.2f}, SAP: {sap_eq:.2f}')
result.to_csv(f'result.csv')
if __name__=='__main__':
main()
これで終わりです。あとはターミナルで
python main.py
してください。流石に前回の囚人のジレンマゲームよりは複雑で長くなりましたが、マルチエージェントシステムでモデル化すると病気の伝染の様子をとても直感的に記述できて、かつ非常に自由度の高いモデルを比較的簡単に組めることが伝わっていれば満足です。
計算結果はどうなるの?
上のコードで計算した結果を可視化したのが以下のヒートマップです。CrとEffectivenessの異なる121通りの組み合わせのそれぞれについて、十分社会が進化した後の最終的な感染者割合(FES),ワクチン接種者比率(VC),社会平均利得(SAP)を載せています。基本的にワクチンの値段が高くて(Crが大きい)ワクチンの効き目が弱い時(Effectivenessが小さい時)には誰もワクチンを打ちたがらないので感染者が増えるという直感に合う結果になっています。最後の社会平均利得については、安いのにとても効き目がある素晴らしいワクチンが登場した時(図の左上の領域)が当然みんな一番幸せになれるよね、という事実を反映した結果になっています。