最尤推定量の性質(BLUE)について（統計検定1級 2024の問題を参考に）

本記事の概要

• 最尤推定量が持つ性質（BLUE）について改めて思い出そう
• 数値シミュレーションで確認しよう

はじめに

統計検定1級2024の問題が公開されました。
統計数理の問1は、線形回帰係数の最尤推定量がもつ基本的な性質、いわゆる BLUE について聞く問題です。
本記事では、その性質について改めて整理して、数値シミュレーションをもとに簡単な確認を行います。

統計検定の問題で問われた内容

統計検定の問題の中で問われた内容と、その背景について簡単に整理します。

以下の読み方

せっかくなので、以下のような形でお読みいただけると嬉しいです。

• 統計検定の問題1の(1)～(5)を順にざっと読む。
• 計算などはせずに(1)～(5)の背景を想像する。
  • 「あの性質を聞いてるんだな」とか「なんか見たことあるな」とか「なんのこと？」とか、いろんな感想があると思います。
• それらを何となく整理したしたうえで、以下の記事を読む。

本記事では、ゴリゴリ計算することよりも問題の背景を味わうことを目的としたいので、良ければお試しください。

出題された問題

問題そのものは掲載することができませんので、こちらのリンクからご確認ください。

解説

問題の解答・解説については色々な方が掲載されていると思います。
例えば、@yoschi_s さんのはてなブログで詳しく解説されています。

問題の背景=BLUE

さて、ここからが本題です。

この問題で問われていることの背景は、線形回帰モデルの最尤推定量がもつ BLUE といわれる性質です。

• BLUE(Best Linear Unbiased Estimator：最良線形不偏推定量)

BLUEとはどういう性質か、線形＋不偏＋最良という3つの部分に分けると以下の通りです。

1. 線形推定量：
   $\hat{\theta}=c_{0}+\sum_{n=1}^{N}c_{n}Y_{n}$ という線形和の形で表される推定量
   　
2. 不偏推定量：
   $E[\hat{\theta}]=\theta$ を満たす（期待値が真値 $\theta$ に一致する)
   　
3. 最良線形不偏推定量：
   線形不偏推定量の中で、分散が最小になる推定量

性質1. は推定量の形に関するものです。
性質2. は推定量の期待値が真値に一致するので、バイアスがない推定量ということです。

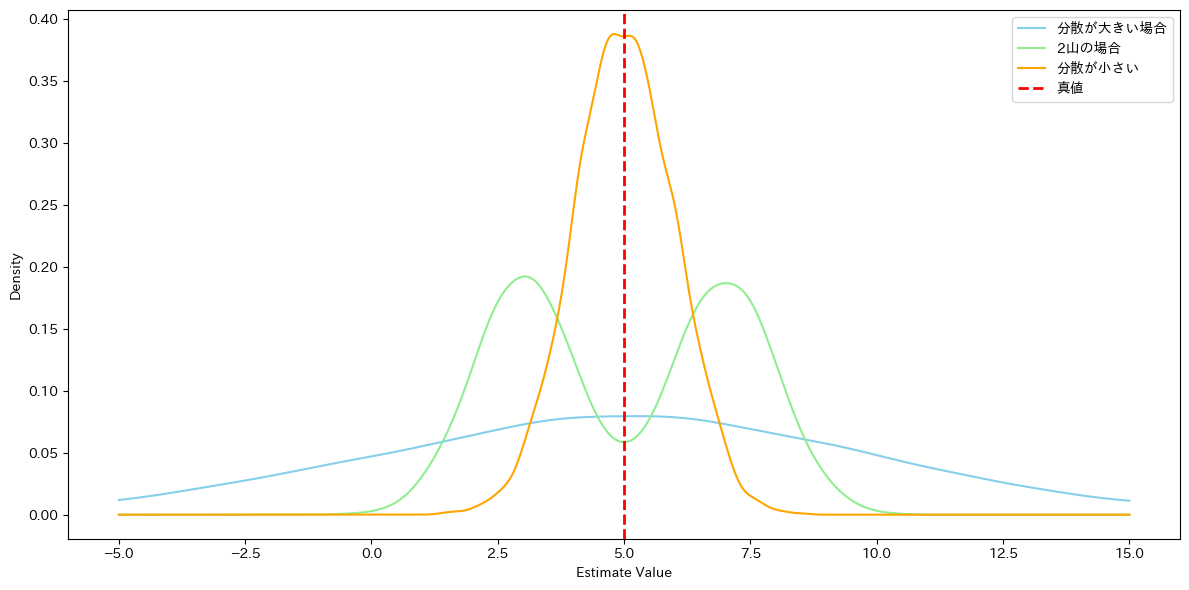
性質2. を満たす時点で推定量としては良さそうですが、期待値が一致するだけでは十分とはいえません。例えば次の図のように、いずれも期待値は$5.0$で分布がまったく違う推定量という場合もありえます。
分散が小さければ真値からのバラつきも小さいため、この場合は黄色の分布をもつ推定量が優れているといえそうです。このように、推定量は期待値に関する性質（不偏性）に加えて、その分散も合わせて評価されます。

つまりどういうこと？？

最尤推定量がBLUEであるとは、
線形不偏推定量の中で分散が最も小さい推定量である
という意味で、最尤推定量はこの性質をもつことが知られています。

このことから、最尤推定量は優れた推定量であると考えられます。

ただし、誤差項の不偏性、均一分散性、無相関性といった仮定を置いています。

ガウス・マルコフの定理

なお、最尤推定量がBLUEであることを示しているのが ガウス・マルコフの定理 です。
ガウス・マルコフの定理についてはこちらが参考になります。

クラーメル・ラオの不等式

不偏推定量の分散に関する重要な内容として、クラーメル・ラオの不等式というものもあります。
簡単のため、推定したいパラメータ $\theta$ を１次元（スカラー）の値としたとき、$\theta$ の不偏推定量 $\hat{\theta}$ について、（いくつかの仮定の下で）以下の不等式が成り立ちます。

　　Var(\hat{\theta}) \geq \frac{1}{I(\theta)}

$Var(\hat{\theta})$ は不偏推定量 $\hat{\theta}$ の分散、$1/I(\theta)$ は $\theta$ のフィッシャー情報量です。

クラーメル・ラオの不等式は、不偏推定量の分散の下限を与える不等式です。言い換えると、次のようになります。

• いろいろある $\theta$ の不偏推定量の分散は、$1/I(\theta)$ よりも小さくすることができない。
• 逆に言えば（対偶を考えれば）、その分散が $1/I(\theta)$ と一致する不偏推定量は、分散を限界まで小さくすることができているので、優れた不偏推定量である、といえる。

先ほど、推定量はその分散でも評価されると書きました。クラーメル・ラオの不等式は、考察したい不偏推定量が、分散の面から言っても優れた推定量であることを示すことに使える不等式です。

問題で問われていることを改めて整理

さてこのあたりで、問題(1)～(5)で問われていることとこれらの性質を対応させてみましょう。
せっかくなので、背景を考えながら問題を読むときのイメージも付記します。

• 問題(1)：対数尤度関数を求める
• 問題(2)：最尤推定量 $\hat{\beta}_{ML}$ が不偏推定量であることを示す
• 問題(3)：回帰係数の真値 $\beta$ の $1/I(\theta)$ を求める
  
  　
• 問題(4)：別の推定量 $\tilde{\beta}$ の期待値と分散を求める
  

• 問題(5)：$\hat{\beta}_{ML}$ と $\tilde{\beta}$ それぞれを用いた検定の検出力を比較
  
  ※推定量の分散が大きいと、第2種の過誤が大きくなり検出力が下がる。

いかがでしょうか？
(5)は検定に関する知識が必要ではありますが、全体を通して不偏推定量の分散について考えている問題であることがわかります。

数値シミュレーション

せっかくなので、数値シミュレーションによって最尤推定量の分散が線形不偏推定量の中で最小であることを簡単に確認してみたいと思います。

シミュレーションで確かめたいこと

統計検定の問題で提示された、2つの線形不偏推定量で比較します。

\begin{align}
\hat{\beta}_{ML}&=\frac{\sum_{n=1}^{N}x_{n}y_{n}}{\sum_{n=1}^{N}x_{n}^2} \\
\hat{\beta}_{Mean}&=\frac{\sum_{n=1}^{N}y_{n}}{\sum_{n=1}^{N}x_{n}} \\
\end{align}

$\hat{\beta}_{ML}$ は、何度も出てきた通り、最尤推定量です。

$\hat{\beta}_{Mean}$ は、問題(4)で提示された不偏推定量です。

それぞれの推定量の分散について、次のことが成り立ちます。

Var(\hat{\beta}_{ML}) \leq Var(\hat{\beta}_{Mean})

このことを、数値シミュレーションで確認します。

シミュレーションコード

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns

# 単回帰モデルのシミュレーション条件
np.random.seed(42)  # 再現性のためのシード値
n = 100  # サンプルサイズ
beta_true = 2  # 真の傾き
sigma = 1  # 誤差の標準偏差

# データ生成
def generate_data(n, beta, sigma):
    x = np.random.uniform(0, 10, size=n)  # 説明変数
    epsilon = np.random.normal(0, sigma, size=n)  # 誤差
    y = beta * x + epsilon  # 目的変数
    return x, y

x, y = generate_data(n, beta_true, sigma)

# 最尤推定量（通常のOLS推定量）の計算
def calculate_mle(x, y):
    beta_mle = np.sum(x * y) / np.sum(x ** 2)
    return beta_mle

beta_mle = calculate_mle(x, y)

# 別の不偏推定量の計算（例: \bar{y}/\bar{x}）
def calculate_alternative(x, y):
    beta_alt = np.mean(y) / np.mean(x)
    return beta_alt

beta_alt = calculate_alternative(x, y)

# 推定量の分散をシミュレーションで比較
n_simulations = 1000  # シミュレーション回数
mle_estimates = []
alt_estimates = []

for _ in range(n_simulations):
    x_sim, y_sim = generate_data(n, beta_true, sigma)
    mle_estimates.append(calculate_mle(x_sim, y_sim))
    alt_estimates.append(calculate_alternative(x_sim, y_sim))

# 結果の可視化 - KDEプロット
plt.figure(figsize=(12, 8))
sns.kdeplot(mle_estimates, label='MLE (OLS)', fill=True, color="blue", alpha=0.6)
sns.kdeplot(alt_estimates, label='Alternative (mean ratio)', fill=True, color="orange", alpha=0.6)
plt.axvline(beta_true, color='red', linestyle='--', label='True Beta')
plt.title('KDE Plot of Estimates')
plt.xlabel('Estimated Beta')
plt.ylabel('Density')
plt.legend()
plt.grid()
plt.show()

# 結果の可視化 - 箱ひげ図
plt.figure(figsize=(12, 8))
plt.boxplot([mle_estimates, alt_estimates],
            labels=['MLE (OLS)', 'Alternative (mean ratio)'],
            patch_artist=True, boxprops=dict(facecolor='lightblue'), medianprops=dict(color='red'))
plt.axhline(beta_true, color='red', linestyle='--', label='True Beta')
plt.title('Boxplot of Estimates')
plt.ylabel('Estimated Beta')
plt.legend()
plt.grid()
plt.show()

# 推定量の分散を計算
def calculate_variance(estimates):
    return np.var(estimates, ddof=1)

var_mle = calculate_variance(mle_estimates)
var_alt = calculate_variance(alt_estimates)

print(f"真値: {beta_true}")
print(f"beta_ML の分散 : {var_mle}")
print(f"beta_Mean の分散: {var_alt}")

シミュレーションの設定を簡単に記します。

• 真のモデル：$y=2.0x+\epsilon_{i},\quad \epsilon_{i}～N(0, 1)$
  • 切片が0の単回帰モデルです。統計検定の問題設定に従いました。
• サンプルサイズ：100
• シミュレーション回数：1000回

推定するのは $x$の係数 2.0です。それぞれの推定量の分布（主に平均、分散）をもとに、比較します。

シミュレーション結果の可視化

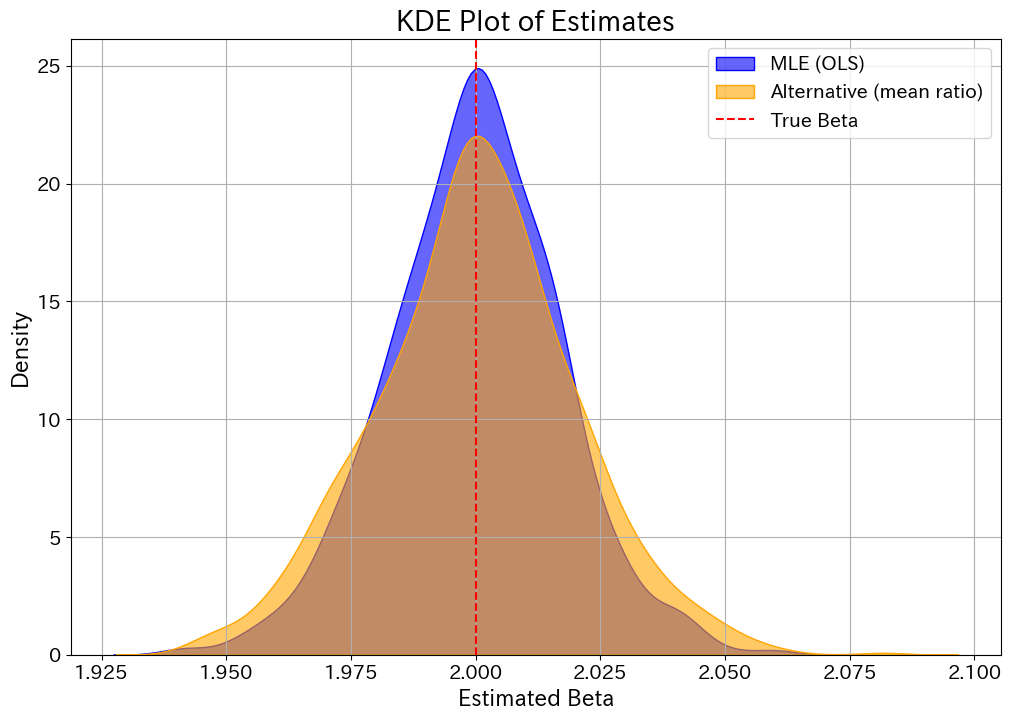
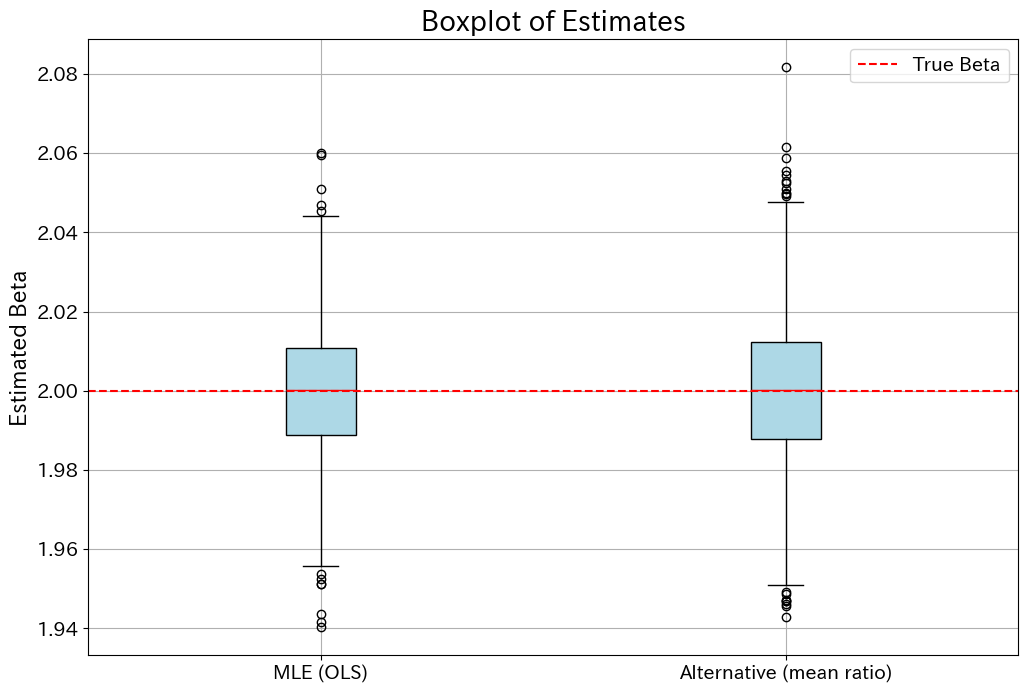
シミュレーション結果を、密度曲線と箱ひげ図で可視化します。

密度曲線

箱ひげ図

どちらの推定量も、平均値で見れば真の値 2.0 を捉えられていることがわかります。
そして$\hat{\beta}_{ML}$ の分布曲線の方が真値あたりで尖っていて、分散が小さくなっているであろうことが読み取れます。

実際に、分散を計算すると以下のようになりました。

推定量	分散
$\hat{\beta}_{ML}$	0.000297780
$\hat{\beta}_{Mean}$	0.000403622

わずかですが、$\hat{\beta}_{ML}$ の方が小さい値になります。
この値自体はサンプルサイズや誤差分散によるのでいろいろ変化し得るものですが、最尤推定量の分散の最小性について少し確認することができました。

といっても、1つの不偏推定量と比較しただけですので、他の不偏推定量との比較もしてみたいところです。

まとめ

本記事では、統計検定の問題をもとに、最尤推定量がもつ性質 BLUE について確認しました。
単に問題を解くだけでなく、本記事を読むことで背景を味わいながら問題を楽しんでいただけていれば嬉しく思います。

参考文献

• 久保川達也. 2017. 現代数理統計学の基礎. 共立出版