概要
配列形式の数独を解くアルゴリズムをSwiftで書いたのでその方法について記事を残します。
いわゆる数独ソルバーです。余談ですが、数独は海外でもSudokuと呼ばれているらしいですね。
コードを書いてみたいが、入力とかを用意するのが面倒な方はLeetCodeの37. Sudoku Solverが同じ内容となっているのでこちらをどうぞ。
関連する記事
Swiftで配列が有効な数独であるかを判定するアルゴリズム
詳細
そもそも数独が何かを知らないと意味が分からないと思うので、まずは数独のルールについて説明します。
数独のルール
数独は、9×9のマスに1から9までの数字を適切に配置するパズルゲームです。以下のルールに従って数字を配置します。
- 各行に1から9までの数字を一度だけ使用する。
- 各列に1から9までの数字を一度だけ使用する。
- 各3×3のブロックに1から9までの数字を一度だけ使用する。
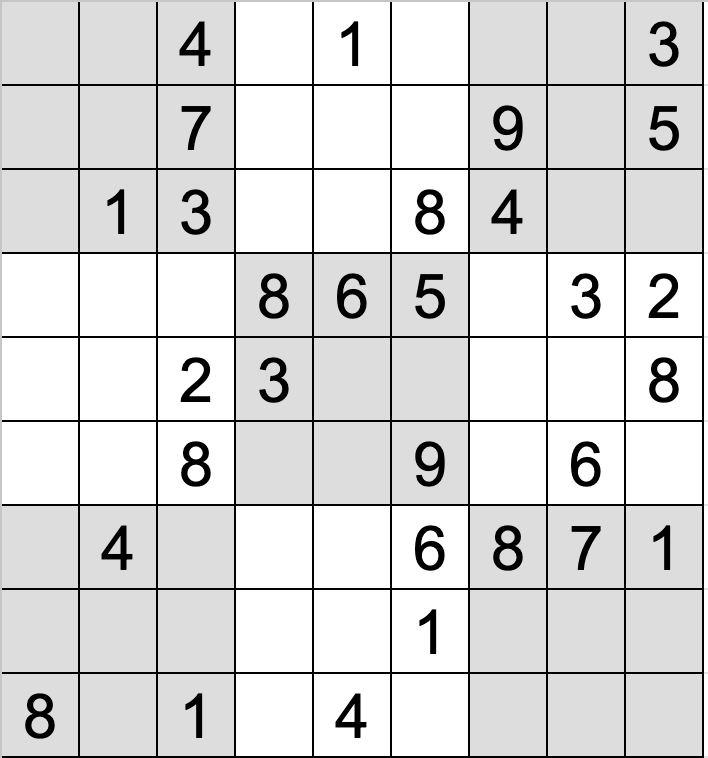
実際の問題では以下のように9×9のマスのうち、特定のマスが埋められた状態のものが与えられます。
一般的には埋められているマスの数が少ければ少ないほど難易度が上がります。
プレイヤーは残りのマスを上記の3点のルールに従って全て埋めます。
今回のアルゴリズムはこのプレイヤーが数独を解くという部分を代わりに行います。
アルゴリズムの実装
今回は数独が二次元配列として渡されます。
例で挙げた画像の場合、以下のような形式となります。
var sudoku: [[Character]] = [
[".",".","4",".","1",".",".",".","3"],
[".",".","7",".",".",".","9",".","5"],
[".","1","3",".",".","8","4",".","."],
[".",".",".","8","6","5",".","3","2"],
[".",".","2","3",".",".",".",".","8"],
[".",".","8",".",".","9",".","6","."],
[".","4",".",".",".","6","8","7","1"],
[".",".",".","3",".","1",".",".","."],
["8",".","1",".","4",".",".",".","."]
]
解法
数独を解くには、バックトラッキングを用いて総当たりで数独の解を探す方法が一般的です。
これは組み合わせが多く存在する場合に、効率的に解を見つけたい時に使用されるアルゴリズムで、代表的な例の一つとして8クイーン問題があります。
バックトラッキングについて
バックトラッキングは、一種の深さ優先探索アルゴリズムです。
問題に対してアプローチを行う過程で解が無効であることが明らかになった時点で、失敗したステップの一つ前のステップに戻って別の方法を試行する「バックトラック」を行います。
数独での例
1.空欄の探索
数独の盤面を左上から右下に向かって走査し、最初に見つかった空欄(配列内の".")を見つけます。
2.数字の試行
空欄に1から9までの数字を一つずつ代入してみます。
代入した数字が数独のルールに従っているかどうかをチェックするため、行、列、および3x3のブロック内でその数字が既に使用されていないかを確認します。(コード内ではチェックのためにisValid関数を使用している)
3.再帰的な探索
ある空欄に対して有効な数字が見つかった場合、その数字を仮に置いてから、再帰的に次の空欄を埋めるために同じ関数(solveSudokuを呼び出している)を呼び出します。
4.バックトラック
再帰的な探索中に解が見つからない場合、つまり、次の空欄に有効な数字がどれも置けない場合には、工程3で置いた数字が間違っていたと判断し、元の空欄に戻って別の数字を試します。
5.解の完成
与えられた数独の盤面のすべての空欄が適切に数字で埋められた場合、数独が解けた解けたという事なので、trueを返して終了します。
すべての数字を試しても解が見つからなかった場合には、falseを返します。
このようなバックトラッキング法は、数独だけでなく他の組み合わせ問題にも応用可能であり、計算機科学における重要なアルゴリズムの一つです。
コード
func solveSudoku(_ board: inout [[Character]]) -> Bool {
for i in 0..<9 {
for j in 0..<9 {
if board[i][j] == "." {
for num in ["1", "2", "3", "4", "5", "6", "7", "8", "9"] {
if isValid(board, i, j, num) {
board[i][j] = num
if solveSudoku(&board) {
return true
}
board[i][j] = "."
}
}
return false
}
}
}
return true
}
func isValid(_ board: [[Character]], _ row: Int, _ col: Int, _ num: Character) -> Bool {
for i in 0..<9 {
if board[row][i] == num { return false }
if board[i][col] == num { return false }
if board[3 * (row / 3) + i / 3][3 * (col / 3) + i % 3] == num { return false }
}
return true
}
以上です。
個人的に有効な数独であるかをチェックする問題よりも難しい問題なので是非解いてみてください。