概要
与えられた配列が有効な数独であるかを判定する方法をSwiftで書いたのでその方法について記事を残します。
コードを書いてみたいが、入力とかを用意するのが面倒な方はLeetCodeの36. Valid Sudokuが同じ内容となっているのでこちらをどうぞ。
詳細
そもそも数独が何かを知らないと意味が分からないと思うので、まずは数独のルールについて説明します。
数独のルール
数独は、9×9のマスに1から9までの数字を適切に配置するパズルゲームです。以下のルールに従って数字を配置します。
- 各行に1から9までの数字を一度だけ使用する。
- 各列に1から9までの数字を一度だけ使用する。
- 各3×3のブロックに1から9までの数字を一度だけ使用する。
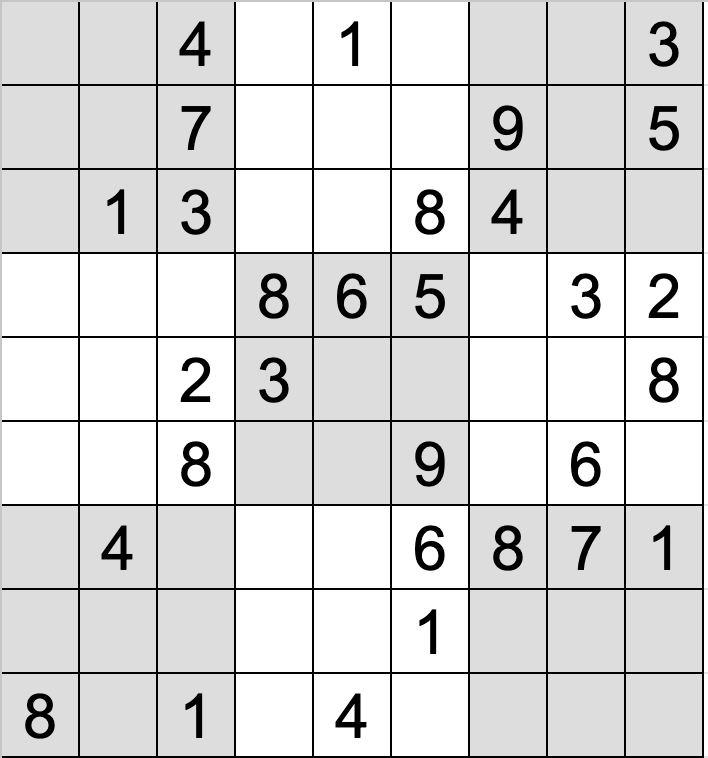
実際の問題では以下のように9×9のマスのうち、特定のマスが埋められた状態のものが与えられます。
一般的には埋められているマスの数が少ければ少ないほど難易度が上がります。
プレイヤーは残りのマスを上記の3点のルールに従って全て埋めます。
アルゴリズムの実装
今回は数独が二次元配列として渡されます。
例で挙げた画像の場合、以下のような形式となります。
let sudoku: [[Character]] = [
[".",".", "4", ".", "1", ".", ".", ".", "3"],
[".",".", "7", ".", ".", ".", "9", ".", "5"],
[".","1", "3", ".", ".", "8", "4", ".", "."],
[".", ".",".", "8", "6", "5", ".", "3", "2"],
[".", ".","2", "3", ".", ".", ".", ".", "8"],
[".", ".","8", ".", ".", "9", ".", "6", "."],
[".", "4",".", ".", ".", "6", "8", "7", "1"],
[".", ".",".", ".", ".", "1", ".", ".", "."],
["8", ".","1", ".", "4", ".", ".", ".", "."]
]
解法1
この問題を解くとき、すぐに思いつく解き方としては以下のようなものがあるでしょう。
func isValidSudoku(_ board: [[Character]]) -> Bool {
for i in 0..<9 {
for j in 0..<9 {
if board[i][j] != "." {
// 1.行チェック
for k in 0..<9 {
if k != j && board[i][k] == board[i][j] {
return false
}
}
// 2.列チェック
for k in 0..<9 {
if k != i && board[k][j] == board[i][j] {
return false
}
}
// 3.ボックスチェック
let boxStartRow = (i / 3) * 3
let boxStartCol = (j / 3) * 3
for row in boxStartRow..<boxStartRow + 3 {
for col in boxStartCol..<boxStartCol + 3 {
if row != i && col != j && board[row][col] == board[i][j] {
return false
}
}
}
}
}
}
return true
}
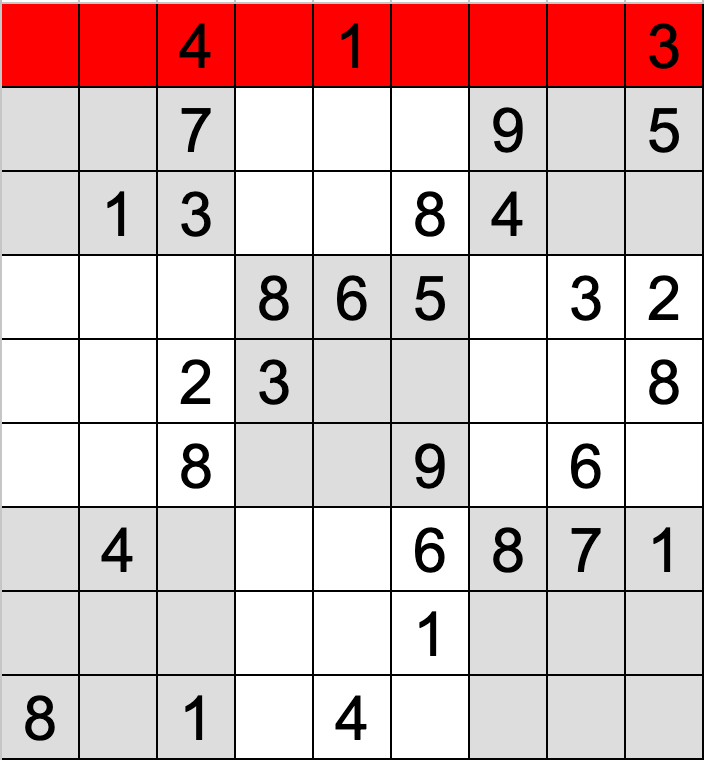
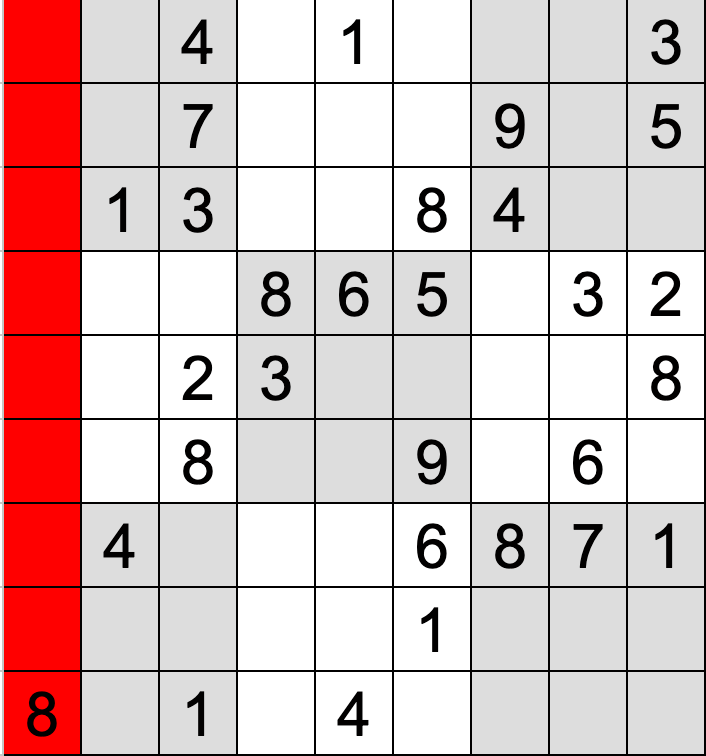
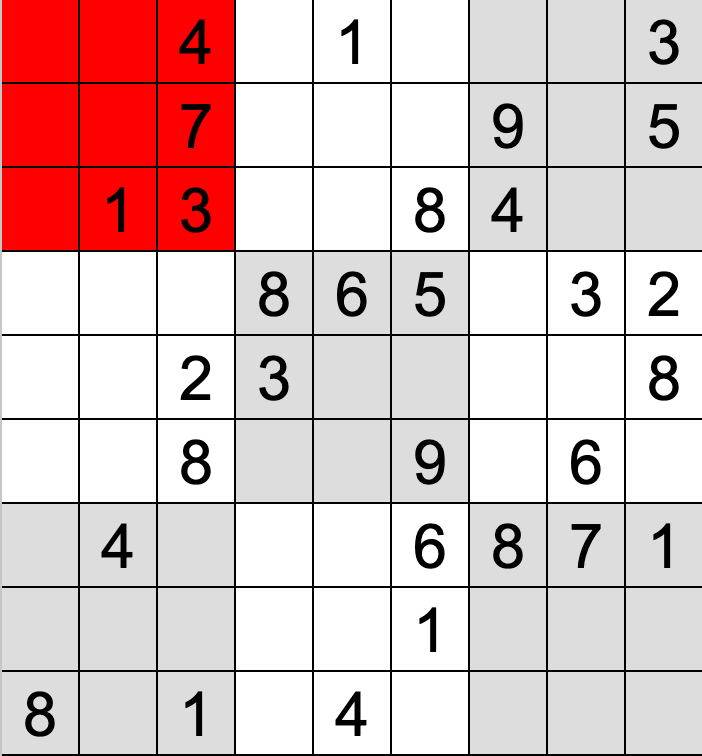
この方法では、行、列、3×3のボックスに対して2重for文の中でさらにfor文(ボックスのチェックは2重for文)を回すことによって行、列、ボックス内に数字の重複がないかをチェックしています。
具体的なイメージは以下の通りです。
それぞれの工程で一つでも数値の重複がある場合には有効な数独ではないと判定できます。
今回は入力が9×9の二次元配列と限定されているため、ではありませんが、4重にfor文を回すとなると、お世辞にも効率が良い解き方とは言えません。
こちらの計算量はO(n^4)となります。
解法2
解法1での問題点は、毎回チェックのために各要素(行、列、ボックス)の全ての値をfor文でチェックしているところにあります。
そこで、計算量を削減するために、毎回チェックするために配列内を走査するのではなく、Setを使用した解き方に切り替えてみます。
以下が修正したコードになります。
func isValidSudoku(_ board: [[Character]]) -> Bool {
let N = 9
var rows = Array(repeating:Set<Character>(),count:N)
var cols = Array(repeating:Set<Character>(),count:N)
var boxes = Array(repeating:Set<Character>(),count:N)
for r in 0..<N{
for c in 0..<N{
let val = board[r][c]
if val == "."{
continue
}
// 1.行チェック
if rows[r].contains(val){
return false
}
rows[r].insert(val)
// 2.列チェック
if cols[c].contains(val){
return false
}
cols[c].insert(val)
// 3.ボックスチェック
let idx = (r/3) * 3 + c / 3
if boxes[idx].contains(val){
return false
}
boxes[idx].insert(val)
}
}
return true
}
毎回愚直に配列内の全ての値をチェックするのではなく、Setでチェックした値を保持し続けることによって、メモリの使用量は多くなりますが、純粋な計算量は削減できます。
こちらの計算量はO(n^2)となります。
計算量の削減と実行時間の相関
実際に計算量が減った、といっても分かりづらいと思うので、解法1と2の実行時間をPlayground上で比較してみます。
解法1と2に対して、先述の二次元配列(sudoku)を渡して実行したところ、以下のように実行時間に差が生まれました。
| 解法1 | 解法2 | |
|---|---|---|
| 実行時間 | 0.04162096977233887 秒 | 0.017665982246398926 秒 |
やはり計算量が少ない解法2の方が実行時間が短くなりました。
正確な差を測るためには試行回数と入力のパターンが足りませんが、計算量を減らすことによって実行時間が短くなることをイメージできるかと思います。