はじめに:冷戦と動的計画法
動的計画法とは何でしょうか?
いきなりですが、日本語版Wikipediaを引用します。
動的計画法(どうてきけいかくほう、英: Dynamic Programming, DP)は、計算機科学の分野において、アルゴリズムの分類の1つである。対象となる問題を複数の部分問題に分割し、部分問題の計算結果を記録しながら解いていく手法を総称してこう呼ぶ。
おそらく、Qiitaを見る人の大半もこのような認識ではないでしょうか。
「あーなんかナップサック問題とか解くんでしょ? 表の数字を端から埋めていくやつ」
というイメージがあるのではないでしょうか(偏見)。
では次に、英語版Wikipediaを見てみましょう。冒頭を日本語訳します。
Dynamic programming - Wikipedia
動的計画法は、数理最適化手法ならびにコンピュータプログラミング手法である。この手法は1950年台にリチャード・ベルマンによって開発され、航空宇宙工学から経済学まで広い分野で応用された。どちらに文脈においても、複雑な問題をより簡単な部分問題へと再帰的に単純化することを指す。ある種の決定問題はこのように分けることはできないが、いくつかの時点にまたがる決定ならば、しばしば再帰的に分けられる。同様に、計算機科学において、もしある問題が部分問題に分けられ、それから再帰的に各部分問題の最適解を見つけることによって最適に解くことができるならば、それは「部分構造最適性を持つ」と言われる。
日本語版よりもちょっと記述が詳しくなりました。ここで注目したいのは、英語版では**「時間的広がりを持つ問題を扱う」**という主張がされている点です。これこそ、「動的計画法」が「動的(dynamic)」と呼ばれているゆえんです。実際、単に「部分問題に分ける」という性質だけでは、いったい動的計画法の何が「動的」なのか伝わりません。そういう意味で、日本語版の記事は今ひとつ説明に物足りなさを感じます(確かに、アルゴリズムとしての動的計画法の応用範囲は、必ずしも時間的広がりを持つ問題に限られているわけではないので、有名無実化しているネーミングではあるのですが……)。
同じく英語版Wikipediaの記事の下の方に、「動的計画法」という名前の由来に関する興味深いエピソードがあります。動的計画法の開発者であるリチャード・ベルマン自身の言葉とされています。
私は(1950年の)秋の四半期をランド研究所で過ごした。私の最初の仕事は、「多段階の決定過程」のために名前を探すことだった。一体、「動的計画法」という名前はどこから来たのだろうか……興味深い質問だ。1950年代は、数学的な研究にとって良い年ではなかった。ウィルソンという名の、とても興味深い紳士がワシントンにいた。彼はアメリカ合衆国の国防長官で、「研究」という言葉に病的なまでの恐怖と憎悪を抱いていた。軽々しく言っているわけではない、正確な表現だ。もし人々が「研究」という言葉を彼の前で使うと、彼は顔が真っ赤になり、暴力的になってしまう。では、「数学」という言葉を彼がどう感じるか……想像できることだろう。ランド研究所は空軍に雇われており、空軍はウィルソンを上司に持っていた。したがって私は、ウィルソンと空軍から、ランド研究所で私が「数学」をやっているという事実を隠さなければならない、そう感じた。どんなお題目、どんな名前を選ぶべきだろうか? まず第一に私は計画立案(planning)、意思決定(decesion making)、思考(thinking)という言葉に興味があった。しかし「計画立案」は、様々な理由によって良い言葉ではない。私はそれゆえ、「計画法(programming)」という言葉を使うことに決めた。そしてこれが動くものであり、多段式であり、時間的に変化するものであるという考えを理解させたかった。「一石二鳥だ!」と私は思った。古典物理において絶対的に正確な意味を持つ単語、「動的(dynamic)」を使おう。それは形容詞としても非常に興味深い性質がある。つまり、「動的」という言葉を侮蔑的な意味で使うことは不可能なのだ。「動的」に侮蔑的な意味を与えるような言葉の組み合わせを考えてみて欲しい……不可能だ! したがって、「動的計画法(dynamic programming)」というのは良い名前だ。私はそう思った。それは連邦議会議員でさえ反対できなかった。だから私はそれを、私の活動のための「傘」として使ったのだ。
偉い人の基礎研究に対する理解のなさは、時と場所を越えてどの組織でも共通する問題のようですね。なお、実際はウィルソンの就任前からベルマンは動的計画法という言葉を論文で使っているので、このエピソードは「盛った」ものだろうと考えられます。
ともあれ、アメリカ空軍の資金的サポートに支えられて「動的計画法」が発展したというのは歴史的事実なわけです。ここで「一体なぜ空軍が?」と疑問に思う方もいらっしゃるかもしれません。これは時代背景を考えてみると、ちょっと面白い構図が浮かび上がってきます。第二次大戦直後のアメリカといえば、東西冷戦。つまり、ソ連との宇宙開発競争が背景にあったわけです。宇宙船を月まで飛ばすためには、限られた燃料の中でうまくスラスター出力を制御し、最適な軌道に乗せなければなりません。「最小の燃料で目的地まで辿り着くにはどのように制御するべきか?」といった時間的広がりを持つ問題は「最適制御問題」と呼ばれますが、これはまさに動的計画法が応用できる問題なのです。
(pdf) APPLICATIONS OF DYNAMIC PROGRAMMING TO SPACE GUIDANCE, SATELLITES, AND TRAJECTORIES
なお、同時期のソ連にはポントリャーギンという盲目の科学者がいて、彼は「動的計画法」とほぼ等価な「最大原理」というものを発見しています(「最小原理」と呼ばれることもあります。問題が最大化を扱うか最小化を扱うかで呼び名が変わります)。幼い頃に失明したポントリャーギンを母親が献身的に支えることで彼は数学者になれたというWikipediaにも載っている有名なエピソードは涙を誘うものがありますが、国と時代を考えると、こちらの話もやはり盛っているのでは……プロパガンダなのでは……という疑いが個人的には拭えません。。。まあ、このエピソードが真実かどうかは抜きにしても、ポントリャーギンの最大原理は非常に優れた美しい理論なので、彼が歴史に名を残すに値する偉大な人間であることは間違いありません。
さて、そもそも何故アメリカとソ連が宇宙開発競争をしていたのかというと、「ロケットの技術はそのままミサイルの技術に軍事転用できるから」……というのは有名な話です。つまり、ヒジョーに穿った見方をすれば、アメリカとソ連はお互いの国土に核ミサイルをぶち込むため、それぞれ最適制御理論の開発に心血を注いだと言えるでしょう。その結果、西側ではベルマンの手によって「動的計画法」が、東側ではポントリャーギンの手によって「最大原理」が編み出されたというわけです。
前置きが長くなりましたが、私が言いたかったのは、「動的計画法=ナップサック問題を効率よく解ける計算アルゴリズムという見方は、間違っちゃあいないけど、最適制御理論としての側面も忘れないであげてね……」ってことです。
問題:工場の生産スケジュールを最適化する
では、具体的に動的計画法を使って最適制御問題、つまり時間的広がりを持つ問題を解いてみたいと思います。
もちろん、そのような問題は無限にいっぱいあるのですが、ここでは次のような問題を考えてみましょう。
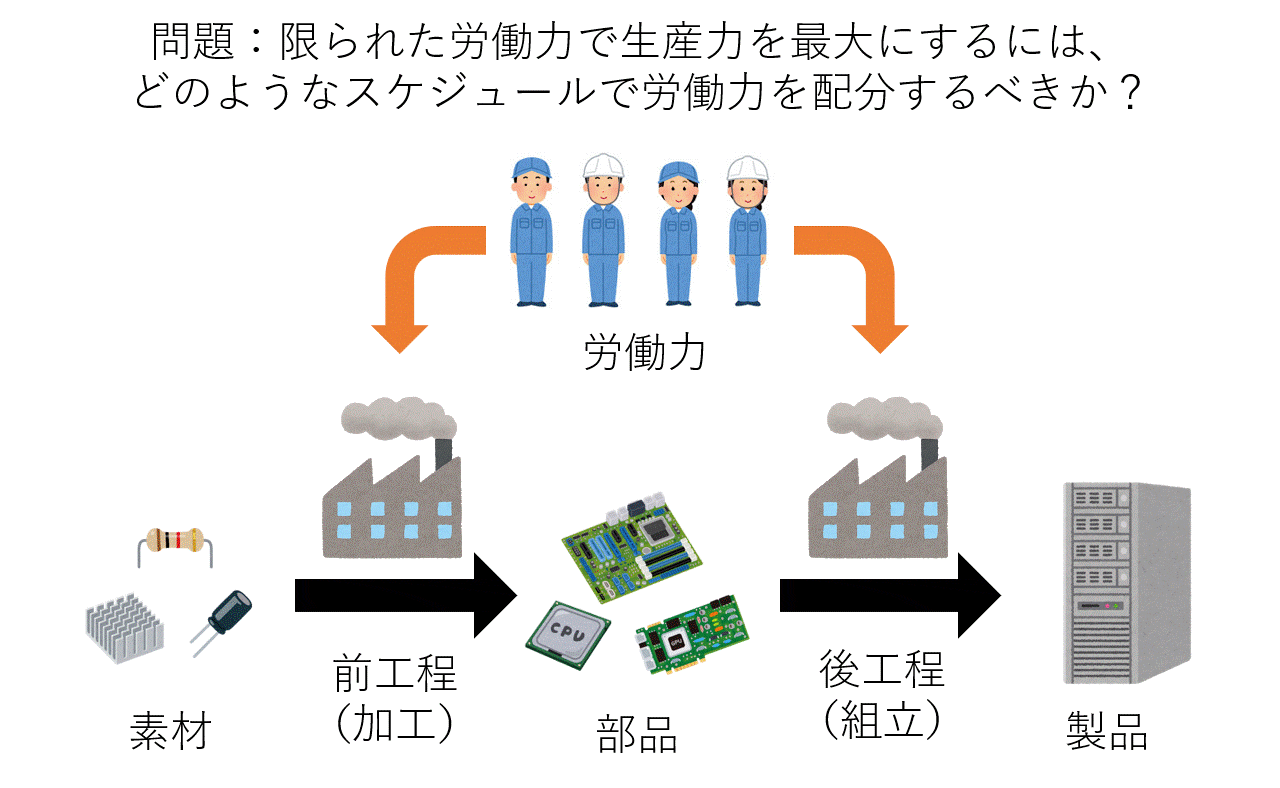
つまり、「素材→(前工程/加工)→部品→(後工程/組立)→製品」という製造工程の生産力を最大にしたいとき、限られた労働力をどのようなスケジュールで前工程と後工程に割り振るべきか?という問題です。自然言語のままだと抽象的すぎるので、微分方程式でえいやっと問題を定式化してあげます。色々バリエーションは考えられますが、今回はやや人工的だけど簡単な問題設定にしておきます:
\max_{E_1, E_2} M_3 (T) \\
\text{subject to} \\
E_1(t)\ge 0,\, E_2(t)\ge 0,\, E_1(t) + E_2(t) = E_{tot}, \\
M_1(0) = M_{tot},\, M_2(0) = M_3(0) = 0,\\
\frac{dM_1}{dt} = -k_1 E_1(t) M_1, \\
\frac{dM_2}{dt} = k_1 E_1(t) M_1 - k_2 E_2(t) M_2, \\
\frac{dM_3}{dt} = k_2 E_2(t) M_2, \\
\text{for }t \in [0,T].\\
ここで、製造業(Manufacture)のMを取って、素材の数を$M_1$、部品の数を$M_2$、製品の数を$M_3$と置き、従業員(Employee)のEを取って、前工程に当てられる労働力を$E_1$、後工程に当てられる労働力を$E_2$と置きました。それぞれ時間$t$の関数で、$t$は$0$から$T$の間を動きます。「初期状態に素材$M_1$だけが$M_{tot}$ある状態で、有限期間$[0,T]$の間に$E_1, E_2$を制御して、最終的にどれだけ$M_3$を生産できるか?」という問題です。$k_1$と$k_2$はそれぞれ前工程、後工程の効率を表すパラメータで、値が大きいほど「その工程が進みやすい」ことを意味しています。従業員の総人数は$E_1+E_2=E_{tot}(定数)$で、常に一定としています。実際にはひとりの同じ従業員が別々の工程を行ったり来たりするということは考えにくいですが、まあ兎に角それぞれの工程を動かす力があり、その力の総数は限られているものだということです。例えば、電力(Electric power)のEと読み直してもOKです。
問題の設定は以上です。
解法:動的計画法(ベルマン方程式)
解法の説明に移りましょう。動的計画法の出番です。
まず、**価値関数(value function)**と呼ばれるものを定義する必要があります。これは問題の形式から自動的に決まります。今回の場合は、次のようなものになります:
$$
V(t,\boldsymbol{M}(t)) \overset{\mathrm{def}}{=} \max_{\boldsymbol{E}[t,T]} M_3(T)
$$
ここで簡単のため$ \boldsymbol{M} = ( M_1,M_2,M_3 ) ,\boldsymbol{E} = (E_1,E_2) $とベクトル表記にしました。また、$\boldsymbol{E}[t,T]$とは、関数$\boldsymbol{E}$の時刻$t$から$T$の値全体を指します。つまり価値関数とは、ある時間のある状態について定まる関数であり、**「それ以降に最適な制御をした場合、どれだけの報酬を得られるか?」**を表す関数です。理論上の最大利得と言ってもいいでしょう。ただしあくまで$t$の関数であることに注意です。問題自体は$t=0$から始まっているので、時刻$t=0$における理論上の最大利得$ V(0,\boldsymbol{M}(0)) $が実際に達成されるべき利得あるいは報酬です。
次に、微小な時間区間$\Delta t$に着目して、価値関数をほんのちょっぴり式変形してみましょう。
V(t,\boldsymbol{M}(t)) = \max_{\boldsymbol{E}[t,T]} M_3(T) \\
= \max_{\boldsymbol{E}(t)} \left[ \max_{\boldsymbol{E}[t+\Delta t,T]} M_3(T) \right] \\
= \max_{\boldsymbol{E}(t)} \left[ V(t+\Delta t,\boldsymbol{M}(t+\Delta t)) \right]
このほんのちょっぴりの式変形こそが動的計画法の真髄であり、この最後の式こそがベルマン方程式と呼ばれるものです。なお、この式を$\Delta t \rightarrow 0$の極限に飛ばしたものは偏微分方程式になり、**ハミルトン=ヤコビ=ベルマン方程式(HJB方程式)**と呼ばれます。HJB方程式からポントリャーギンの最大原理を導くことができますが、今回は詳細を省きます。なお、ポントリャーギン自身は別の方法(ワイエルシュトラスの条件と呼ばれる一種の変分法)で最大原理を導いています。
式変形を解説していきましょう。
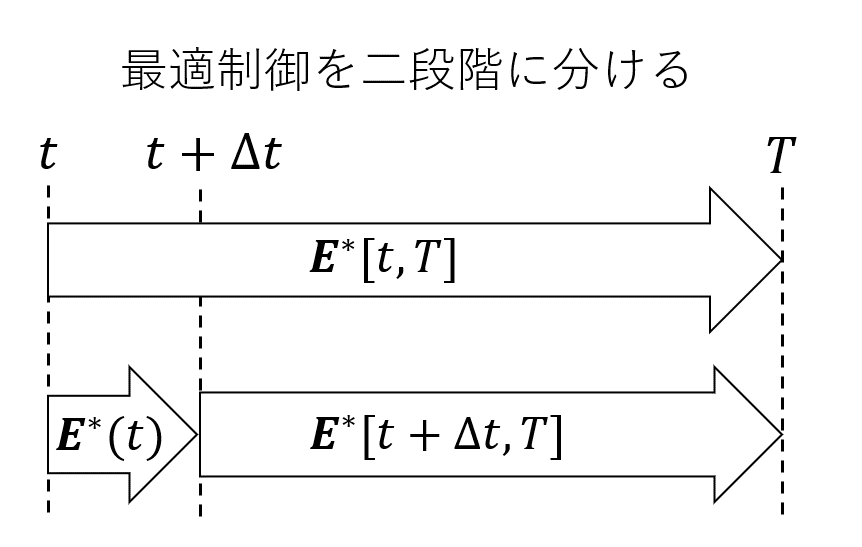
一行目から二行目で、制御(意思決定)を二段階にわけました。つまり、「$t$から$T$までの最適な制御$\boldsymbol{E}^* [t,T]$」は、「『$t+\Delta t$から$T$までの最適な制御$\boldsymbol{E}^* [t+\Delta t,T]$』と『$t$における最適な制御$\boldsymbol{E}^* (t)$』を組み合わせたもの」と同じはずです。この決定は独立にばらばらに行われるものではなくて、入れ子構造(ネスト)になっていることに注意です。$[t+\Delta t,T]$が内側(先に最適化される)で、$t$が外側(後で最適化される)です。
二行目から三行目は、ただ価値関数の定義を適用しただけですが、おかげで価値関数の$t$と$t+\Delta t$における関係、要は漸化式が作れました。ただし「後ろ向き」の漸化式です。高校数学で出てくるような数列の漸化式は「前向き」で、$t+\Delta t$における値を$t$の関数として書けるものがほとんどだったはずですが、ここでは$t$における値を$t+\Delta t$の関数として書いています。そのため、高校数学の前向き漸化式が「最初の値」を必要としていたのに対して、後ろ向き漸化式では「最後の値」を必要とします。
幸い、定義から、価値関数の終端条件は次のように自動的に定まります。
$$
V(T,\boldsymbol{M}(T)) = M_3(T)
$$
これがわかれば後は高校数学です。漸化式は、ある瞬間の最適制御を求めるという小さな最適化問題になっています。この漸化式を$t=T$から逆向きに解いていき、その過程で得られる瞬間瞬間の最適な制御$\boldsymbol{E}^* (t,\boldsymbol{M}(t))$を記憶しておきます(ただし$V$も$\boldsymbol{E}^* $も$t$だけでなく$\boldsymbol{M}$の関数でもあるため、各$\boldsymbol{M}$について求めなければなりません。高校数学でいうと、数列が複数あって相互依存している状態です)。$V$が$t=0$まで求まったら、今度は与えられた初期値$\boldsymbol{M}(0)$を使って今度は順向きに$t=0$から$t=T$までの最適な軌道$\boldsymbol{M}^* (t) $と、その軌道上における最適な制御$\boldsymbol{E}^* (t,\boldsymbol{M}^* (t))$を求めていけばよいわけです。
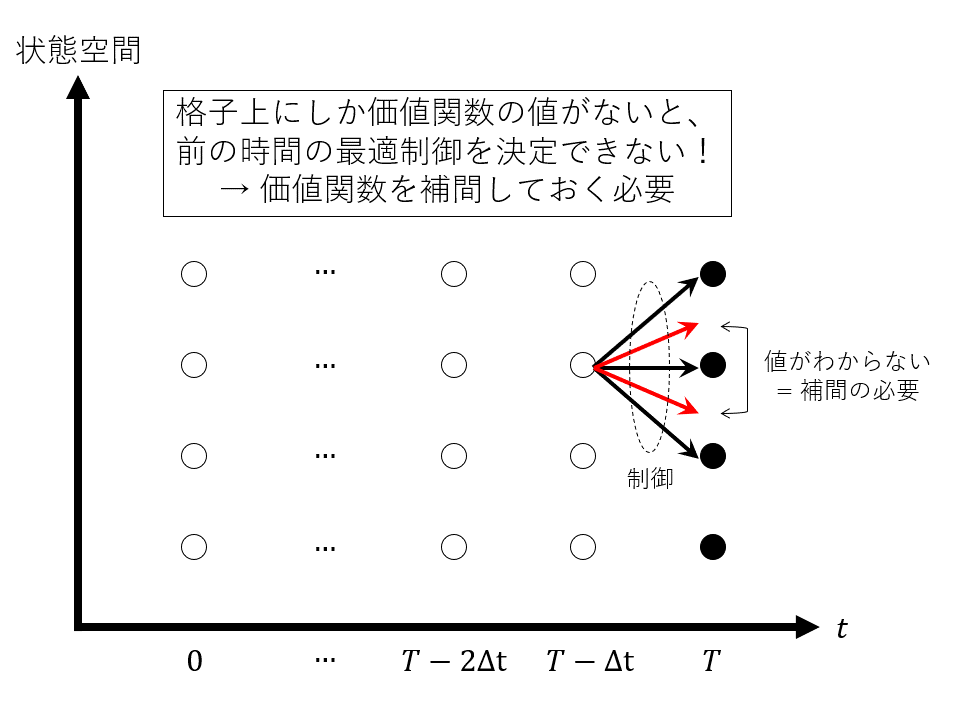
ここまで聞くと「あ~なるほどね~、ナップサック問題の解き方と似てるや~ん。状態変数を離散化すれば、結局は表の穴埋めでしょ?」って感じがするかもしれません。「じゃ、いっちょ数値計算してみっか~」いいでしょうやってみましょう。ところが実際に実装してみようとすると、ひとつの壁にぶつかります。それは今回のように状態変数が連続の問題を扱う場合、格子上だけで求めた$t+\Delta t$における価値関数はスカスカであるため、対応する軌道が取れず、$t$における最適制御の決定ができないという問題です。時間変数の離散・連続とは関係なく、状態変数が連続の場合にこの問題は起こります。漸化式が最適化問題になっているために起こる問題です。
どんなに格子間隔を細かく取っても無駄です。うまく格子点の間だけを推移してくれるケースなど非常に限られています。これは仕方ありません。価値関数を適当に補間するしかないでしょう(軌道を無理やり最近傍の格子点に修正するという手段も考えられそうですが、関数補間の場合よりももっと細かく格子間隔を取る必要が生じるでしょう)。また状態空間の境界(格子点の端っこ)を軌道がはみ出してしまう問題などもありますが、これも価値関数の外挿で対処します(これもやはり軌道の方を修正するという方法が考えられます)。この辺の問題は、以下の資料が参考になるかと思います。
(pdf) 動的計画法を用いた列車運転曲線最適化問題の求解法
(pdf) ある在庫管理問題の動的計画法による解法と CUDAを用いた高速化
解答:必要な物を、必要な時に、必要な量だけ生産する
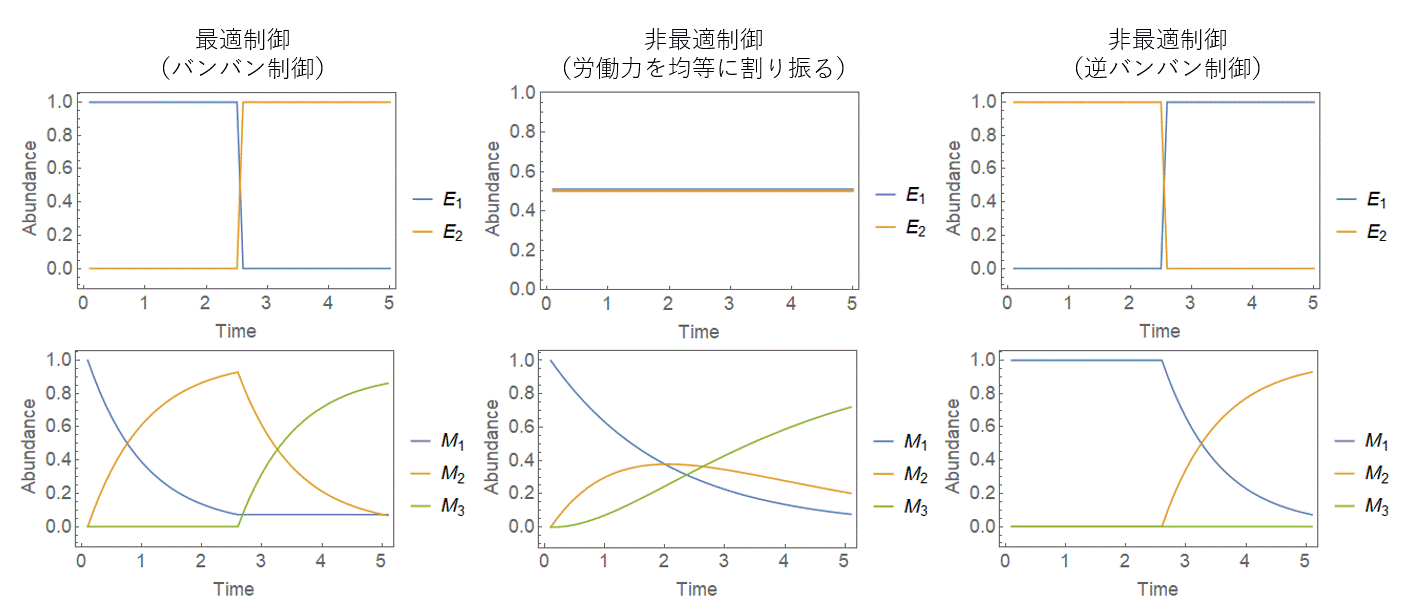
諸問題を乗り越え、どうにかこうにか数値計算をすると、次のような結果が得られます。
ここで、最大時間$T$は5、残りのパラメータはすべて1と置きました($M_{tot}=E_{tot}=k_1=k_2=1$)。左端が最適制御で、右2つは比較のため適当な制御の下での試行を示しています。確かに、左端は右2つよりも最終生産物は多く得られていますが……果たして、この数値的に求めた解は、本当に「最適」なのでしょうか? 幸い、今回の問題はポントリャーギンの最大原理を使って解析的に解くことが出来るので、その解答と比較してみましょう。詳細は省きますが、$k_1=k_2$のとき、答えは非常に簡潔に書けます:
(E^*_1, E^*_2) = (E_{tot}, 0) ~~~ \text{for} ~~~ 0\le t< T/2 \\
(E^*_1, E^*_2) = (0, E_{tot}) ~~~ \text{for} ~~~ T/2\le t< T
確かに、これは動的計画法で求めた最適制御(=左端の図が表している区分的直線)の数式による表現になっています。
こうした急激に変化する制御=バンバン変化する制御は、バンバン制御(bang-bang control)と呼ばれます。馬鹿みたいな名前ですが、れっきとしたテクニカルタームです。時間変数と状態変数が連続であっても、最適制御は不連続になるというのが、バンバン制御の面白いところだと思います。
最後に、得られた最適制御の解釈をしてみましょう。簡単に言うとこの制御は**「計画期間の前半では前工程に全力を注ぎ、後半では後工程に全力を注ぐ」ということになっています。その結果、終端時間における材料・部品の在庫が最少に抑えられ($T$における$M_1,M_2$が非最適制御の場合よりも少ない)、最初にあった材料のほぼすべてが最終生産物に変換されています。後工程で必要となる分しか、前工程では生産しないわけです。この辺はトヨタのカンバン方式(ジャストインタイム生産システム)の理念「必要な物を、必要な時に、必要な量だけ生産する」**に通じるものがあり、直感的にも納得行く解になっているかと思います。
おわりに:ごめんなさい
本記事は制御工学 Advent Calendar 2018の12月23日の記事として用意したものです。……が、筆が遅くて日付を跨いでしまいました。本当にすみません! 本当は最適制御問題において動的計画法を使うことのメリット(確率を扱いやすい)・デメリット(次元の呪いを受けやすい)なども詳しく語りたかったのですが、時間と体力的にもう限界です……投稿させてください……。もしも記事中でなにかトンチンカンなことを言っていたら、遠慮なくコメント欄でご指摘ください。何はともあれ、最後まで読んでいただきありがとうございました!
コード:Mathematica
(*Backward Process*)
Clear[V, Vip];
tmax = 5; \[CapitalDelta]t = 1/10;
Mtot = 1; \[CapitalDelta]M = 1/100;
Etot = 1.; \[CapitalDelta]E = 1/10;
LatticeOffset = \[CapitalDelta]M;
E2[E1_] := Etot - E1;
(*補間関数のための非構造格子の生成:面積ゼロの要素を省く必要あり:境界より少しはみ出しておく*)
FeasibleM =
Flatten[Table[
N@{M1, M2}, {M1, 0, Mtot + LatticeOffset, \[CapitalDelta]M}, {M2,
0, Mtot - M1 + LatticeOffset, \[CapitalDelta]M}], 1];
Needs["NDSolve`FEM`"]
Quiet[mesh = ToElementMesh[FeasibleM]];
good = Flatten@Position[mesh["Quality"][[1]], _?Positive];
mesh2 = ToElementMesh["Coordinates" -> mesh["Coordinates"],
"MeshElements" -> {TriangleElement[
mesh["MeshElements"][[1, 1, good]]]}];
(*DP*)
AbsoluteTiming@Block[{Vtemp, Border},
(*Initialization for feasible area*)
Do[V[t] =
Table[{(*Null*)0., 0.(*Infeasible region*)}, {M1, 0,
Mtot, \[CapitalDelta]M}, {M2, 0,
Mtot - M1, \[CapitalDelta]M}], {t, 0, tmax, \[CapitalDelta]t}];
(*Boundary condition*)
V[tmax] =
Table[{(*Null*)0., N@Mtot - (M1 + M2)(*M3:Terminal cost*)}, {M1, 0,
Mtot, \[CapitalDelta]M}, {M2, 0, Mtot - M1, \[CapitalDelta]M}];
(*Recursion*)
Do[
(*Interpolation of Value function at t+\[CapitalDelta]t*)
(*価値関数の境界だけ手で外挿しておく*)
Vtemp =
Join[Table[
V[t + \[CapitalDelta]t][[1 + M1/\[CapitalDelta]M,
1 + M2/\[CapitalDelta]M, 2]], {M1, 0,
Mtot, \[CapitalDelta]M}, {M2, 0,
Mtot - M1, \[CapitalDelta]M}], {{}}];
Border =
Join[{{V[t + \[CapitalDelta]t][[1, 1 + Mtot/\[CapitalDelta]M,
2]]}}, Table[(
V[t + \[CapitalDelta]t][[M1/\[CapitalDelta]M,
1 + M2/\[CapitalDelta]M, 2]] +
V[t + \[CapitalDelta]t][[1 + M1/\[CapitalDelta]M,
M2/\[CapitalDelta]M, 2]])/
2, {M1, \[CapitalDelta]M, Mtot, \[CapitalDelta]M}, {M2,
Mtot + \[CapitalDelta]M - M1,
Mtot + \[CapitalDelta]M -
M1, \[CapitalDelta]M}], {{V[t + \[CapitalDelta]t][[
1 + Mtot/\[CapitalDelta]M, 1, 2]]}}];
Vtemp = Table[Join[Vtemp[[i]], Border[[i]]], {i, Length@Border}];
Vtemp = Flatten[Vtemp, 1];
Vip = ListInterpolation[Vtemp, mesh2, InterpolationOrder -> 1];
(*Determination of Value function at t*)
V[t] = Table[
(*各格子点において部分問題を解く。MaximalByを使うよりこちらが早い*)
Block[{Vmax, Vnow, Eopt},
Vmax = -Infinity;
Do[
Vnow =
Vip[M1 + \[CapitalDelta]t (-E1 M1),
M2 + \[CapitalDelta]t (E1 M1 - E2[E1] M2)];
If[Vnow > Vmax, Vmax = Vnow; Eopt = E1];
, {E1, 0, Etot, \[CapitalDelta]E}];
{Eopt, Vmax}
]
, {M1, 0, Mtot, \[CapitalDelta]M}, {M2, 0,
Mtot - M1, \[CapitalDelta]M}]
, {t, tmax - \[CapitalDelta]t, 0, -\[CapitalDelta]t}];
]
(*Forward Process*)
(*最後の一点つまりtmaxの入力,E[tmax]はNULLであることに注意*)
Clear[M1D, M2D, M3D, ED]
M1D[0] = Mtot; M2D[0] = 0; M3D[0] = 0;
Do[{
ED[t] =
V[t][[Round[1 + M1D[t]/\[CapitalDelta]M],
Round[1 + M2D[t]/\[CapitalDelta]M], 1]];
M1D[t + \[CapitalDelta]t] =
M1D[t] + \[CapitalDelta]t (-ED[t] M1D[t]),
M2D[t + \[CapitalDelta]t] =
M2D[t] + \[CapitalDelta]t (ED[t] M1D[t] - E2[ED[t]] M2D[t]),
M3D[t + \[CapitalDelta]t] =
M3D[t] + \[CapitalDelta]t (E2[ED[t]] M2D[t])
}, {t, 0, tmax - \[CapitalDelta]t, \[CapitalDelta]t}];
(*表示*)
Grid@Transpose@{{
ListPlot[
Table[{ED[t], Etot - ED[t]}, {t, 0,
tmax, \[CapitalDelta]t}]\[Transpose],
PlotLegends -> {"\!\(\*SubscriptBox[\(E\), \(1\)]\)",
"\!\(\*SubscriptBox[\(E\), \(2\)]\)"}, Joined -> True,
AxesOrigin -> {0, -0.1}, Frame -> True,
FrameLabel -> {"Time", "Abundance"}, ImageSize -> Medium,
LabelStyle -> 18,
FrameTicks -> {{Automatic,
None}, {{Range[0, 50, 10], Range[0, 5, 1]}\[Transpose],
None}}],
ListPlot[
Table[{M1D[t], M2D[t], M3D[t]}, {t, 0,
tmax, \[CapitalDelta]t}]\[Transpose],
PlotLegends -> {"\!\(\*SubscriptBox[\(M\), \(1\)]\)",
"\!\(\*SubscriptBox[\(M\), \(2\)]\)",
"\!\(\*SubscriptBox[\(M\), \(3\)]\)"}, Joined -> True,
AxesOrigin -> {0, -0.1}, Frame -> True,
FrameLabel -> {"Time", "Abundance"}, ImageSize -> Medium,
LabelStyle -> 18,
FrameTicks -> {{Automatic,
None}, {{Range[0, 50, 10], Range[0, 5, 1]}\[Transpose], None}}]
}}