Lua版 ゼロから作るDeep Learning その１１［勾配の算出］

過去記事まとめ

Lua版 ゼロから作るDeep Learning まとめ

はじめに

　今回は原書4章の勾配の部分を実装します。今回の部分は機械学習というよりは基礎的な説明ですので飛ばしても大丈夫です。
　スクリプトは以下の通りです。

gradient_2d.lua

require 'gnuplot'

---勾配算出関数.
-- 入力値に対する多変数関数の勾配を求める
-- @param f 多変数関数 (Type：function)
-- @param x 入力値 (Type：Tensor ※1D Tensor)
-- @return 入力値に対する勾配の値 (Type：Tensor)
function _numerical_gradient_no_batch(f, x)
    local h = 1e-4 -- 0.0001
    grad = x:clone():zero()

    for idx = 1, x:size()[1] do
        local tmp_val = x:float()[idx]
        x[idx] = tmp_val + h --一つの要素だけ動かす
        local fxh1 = f(x) -- f(x+h)

        x[idx] = tmp_val - h 
        local fxh2 = f(x) -- f(x-h)
        grad[idx] = (fxh1 - fxh2) / (2*h)

        x[idx] = tmp_val -- 値を元に戻す
    end

    return grad
end

---勾配算出関数.
-- 入力値（複数）に対する多変数関数の勾配を求める
-- @param f 多変数関数 (Type：function)
-- @param x 入力値 (Type：Tensor)
-- @return 入力値に対する勾配の値 (Type：Tensor)
function numerical_gradient(f, X)
    if X:dim() == 1 then
        return _numerical_gradient_no_batch(f, X)
    else
        local grad = X:clone():zero()

        for idx = 1, X:size()[1] do
            grad[idx] = _numerical_gradient_no_batch(f, X[idx]) --1Dずつ勾配を計算
        end

        return grad
    end
end

---(Σxi^2)他変数関数.
-- @param x 入力値 (Type：Tensor)
-- @return 出力値 (Type：Tensor)
function function_2(x)
    if x:dim() == 1 then
        return torch.sum(torch.pow(x,2))
    else
        return torch.sum(torch.pow(x,2), 2)
    end
end

--{3.0, 4.0}での勾配
print(numerical_gradient(function_2, torch.Tensor({3.0,4.0})))
--{0.0, 2.0}での勾配
print(numerical_gradient(function_2, torch.Tensor({0.0,2.0})))
--{3.0, 0.0}での勾配
print(numerical_gradient(function_2, torch.Tensor({3.0,0.0})))


local x0 = torch.range(-2, 2.5, 0.25)
local x1 = torch.range(-2, 2.5, 0.25)

--{x0[i], x1[j]}での各値に対する勾配(gradx,grady)と関数の値(surface)を計算
local gradx = torch.Tensor(x0:size()[1],x1:size()[1]):zero()
local grady = torch.Tensor(x0:size()[1],x1:size()[1]):zero()
local surface = torch.Tensor(x0:size()[1],x1:size()[1]):zero()
for xi = 1, x1:size()[1] do
    for i = 1, x0:size()[1] do
        gradx[{i,xi}] = numerical_gradient(function_2, torch.Tensor({x0[i], x1[xi]}))[1]
        grady[{i,xi}] = numerical_gradient(function_2, torch.Tensor({x0[i], x1[xi]}))[2]
        surface[{i,xi}] = function_2(torch.Tensor({x0[i], x1[xi]}))
    end
end

--グラフ描写　※x,y軸の目盛りは適当
gnuplot.figure(1)
gnuplot.splot(torch.sqrt(gradx:pow(2)+grady:pow(2))) --勾配の二乗平均
gnuplot.figure(2)
gnuplot.splot(surface) --関数の値

　　
　実行結果は以下の通りです。

実行結果

$ th gradient_2d.lua
 6.0000
 8.0000
[torch.DoubleTensor of size 2]

 0.0000
 4.0000
[torch.DoubleTensor of size 2]

 6.0000
 0.0000
[torch.DoubleTensor of size 2]

　torchの標準でついてくるgnuplotではquiverが描写できないので、代わりにx,yの勾配の根二乗平均を算出してプロットしてみました。ただし申し訳ないのですが、手間暇の関係からx,y軸の目盛りは適当とさせていただきます。10くらいが本来の原点と考えてみてください。
　
　

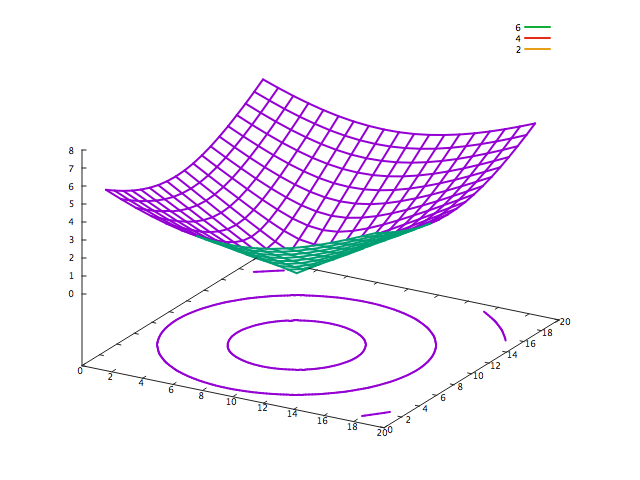
　ついでに関数の値についてのプロットも示します。こちらの方がわかりやすいかもしれません。
　
　

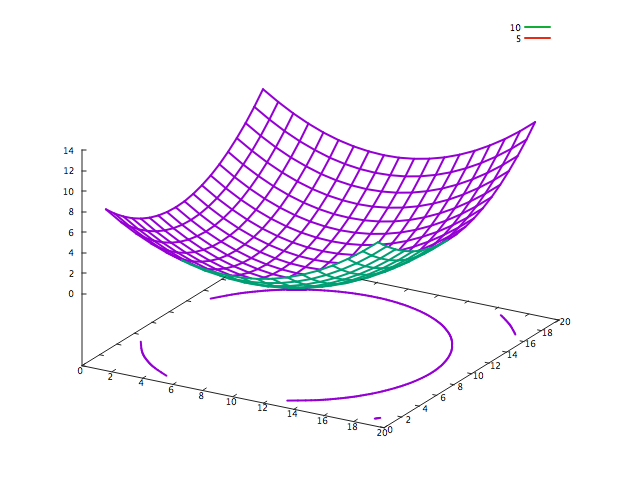
　ちゃんと勾配が計算できてそうですね。

おわりに

　今回は以上です。

　次回は勾配法の場合をみていきたいと思います。やっと機械学習らしい話になるのでやる気になれますね。
　
　ありがとうございました。