はじめに
機械学習の世界ではベイズ最適化を活用した効率的なハイパーパラメータチューニングが当たり前のように使われております。例えば、2015年には東京大学の佐藤先生がベイズ最適化を上手くを活用した実践的な研究成果をご発表されております
この発表で解説されている通り、ハイパーパラメータの選定作業すら機械に任せてしまうことができるため、これ以降もベイズ最適化が昨今の機械学習ブームのさらなる飛躍に貢献していきました。ベイズ最適化が機械学習のハイパーパラメータ選定に使われる理由は大まかに下記の点であるといわれています。
1.ブラックボックス関数(コスト関数)の最大化・最小化を実現できる。
2.グリッドサーチよりもパラメータ調整のための試行回数を大幅に削減できる。
3.確率モデルに基づく方法のため、推定結果の不確かさもモデリングできる。
特に、1番と2番の利点は複雑なコスト関数・対象に対して,なるべく少ない試行回数にて最適解を求解できるという非常に強力な利点といえます。もしこのベイズ最適化を制御系設計のパラメータチューニングに適用できれば、皆様の制御系設計業務の効率化を実現できるかもしれません。しかしながら、制御工学屋さんがベイズ最適化を使おうとすると、大体の人が下記の点で挫折してしまうことがあります。
・統計/確率論に基づく方法のため、確定システムに慣れた制御工学屋には理論がやや難解
・制御系設計向けのサンプルコードが少ない
・ベイズ最適化を制御系設計に適用した事例がそこまで多くないため,例題による実感がわきにくい。
以上の背景のもと、本記事では制御系設計にベイズ最適化を上手く活用していただくことを目指し,なるべく数式を使わずに理論の簡単な部分の解説とサンプルコードを掲載していこうと思います。制御屋さんにとってなじみ深いフィードバック制御器の設計を例題に取り上げ,ベイズ最適化の方法と理屈に関して解説していきます。なお,今回の記事では確率や数式に詳しくない人でも雰囲気をつかめるように,あえて厳密な数式の説明・記載を省略しています。この記事は下記の教科書を参考に作成しておりますので、余力のある方はぜひ参考にしてください。
参考文献:
持橋 大地, 大羽 成征, (2019). ガウス過程と機械学習 (機械学習プロフェッショナルシリーズ), 講談社
問題設定
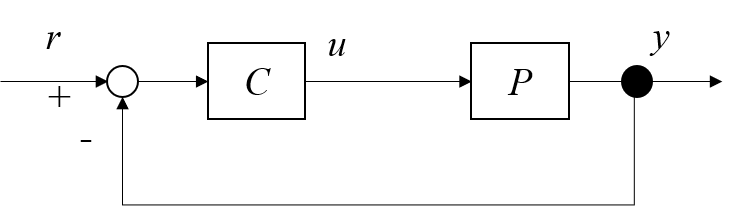
まず,今回対象とするシステムを定義します。Fig.1のフィードバック制御系を考えます。制御対象を未知の特性を有するシステムとしています。制御器の伝達関数$C(s)$は可調整パラメータ$\rho$でパラメタライズされています。閉ループ実験にて,任意のパラメータ$\rho$に対する閉ループ系の出力応答$y(t, \rho)$と入力応答$u(t, \rho)$が得られるとします。例えば,フィードバック制御系における制御系設計では,下記のようなコスト関数
f (\rho):=H(\rho)+\sum_{k=0}^{N}(y(kT_{s},\rho)-r(kT_{s}))^2
を設定することがよくあります。実験データのデータ長が$N$,$T_{s}$がサンプリング時間としています。コスト関数の右辺第二項は目標値と出力間の誤差に関する関数です。右辺第一項は本制御系における制約条件や他の変数に対する罰則項です。もし,最適化における罰則が特になければ$H(\rho)=0$とおいても構いません。今回の問題設定では制御対象の特性が未知のため,パラメータ$\rho$を実際に設定して$y(t, \rho)$を実験にて測定しないとコスト関数の出力$f (\rho)$の値がわかりません。言い換えると,この関数はブラックボックスな関数となっており,机上でのオフラインの数理最適化ができません。したがって,パラメータ$\rho$の値を変えながら何度か実験を繰り返して,$f (\rho)$が十分小さくなるような$\rho$を見つけなければなりません。
以上の問題設定のもと,なるべく少ない実験回数にてコスト関数の出力であるスカラー値を観測しながら,$f (\rho)$が十分小さくなるような$\rho$を見つけることを目指します。なお,ベイズ最適化は関数の形に対して明確な制約があるわけではありません。実際は制御系や要求仕様に応じて,上記の$f(\rho)$以外の形のコスト関数を設定しても問題はありません。
比例制御を通したベイズ最適化の解説
さっそく,ベイズ最適化に関して解説していきます。ここでは,読者の理解を深めるため,もっとも簡単な比例制御の制御系設計を通して解説します。比例制御とPID制御では,可調整パラメータの数が違いますが,どちらの制御系を調整する場合でもベイズ最適化の理屈は同じです。まず,1次元のパラメータ調整の例題を通して,ベイズ最適化の雰囲気をつかんでみましょう。
比例制御におけるゲイン調整問題
Fig.1のフィードバック制御系に対して,制御器の伝達関数$C(s)$が
C(s)=K_{P}
と設定されています。$K_{P}$は比例ゲインであり,$\rho=K_{P}$となります。今回の可調整パラメータです。今回は閉ループ実験にて,任意の$K_{P}$に対する閉ループ系の出力応答$y(t, K_{P})$が得られるとします。今回の制御系では,コスト関数$f(\rho)$を最小化するような比例ゲインを求めることを目指します。この章では,制御系の可調整パラメータが比例ゲインしかないため,以後コスト関数を$f(\rho)$の代わりに$f(K_{P})$と記載しますのでご注意ください。制御対象の特性が未知のため,比例ゲイン$K_{P}$を実際に設定して$y(t, K_{P})$を測定するまで$f (K_{P})$の値がわかりません。したがって,この関数はブラックボックスな関数となっており,机上で最適化できません。比例ゲイン$K_{P}$の値を変えながら何度か実験を繰り返し,$f (K_{P})$が十分小さくなるような$K_{P}$を見つけなければなりません。
以上の問題設定のもと,なるべく少ない実験回数にて$f (K_{P})$が十分小さくなるような$K_{P}$を見つけることを目指します。ただし,比例ゲイン調整におけるパラメータ探索範囲と試行回数は事前に設定しておくものとします。
ベイズ最適化によるゲイン調整の手順
ベイズ最適化におけるゲイン調整の手順としては,まず初期実験を実施します。適当な値の比例ゲイン$K_{1}$を設定して閉ループ実験を実施し,その際のコスト関数のスカラー値$f (K_{1})$を測定しましょう。初期実験の回数は任意の回数で問題ないです。ここでは,適当な値の比例ゲイン$K_{2}$での閉ループ実験も実施し,その際のコスト関数のスカラー値$f (K_{2})$を測定しておきます。
任意の$K_{P}$に対するコスト関数の挙動が何もわからなければ最適化することはできません。したがって,既知の実験結果をもとにコスト関数$f (K_{P})$を推定することを目指します。コスト関数の推定にあたり,$f (K_{P})$がガウス分布に従うと仮定します。数式で表すと,
f (K_{P}) \sim \mathcal{N}(\mu, \sigma)
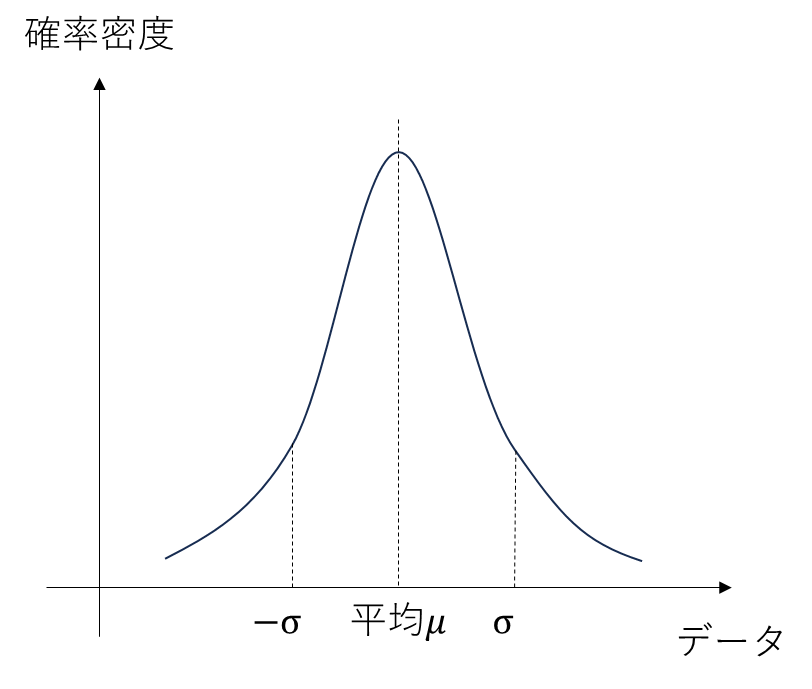
となります。$\mu$が平均,$\sigma$が標準偏差を指します。「ガウス分布ってなに?」と思った方がいらっしゃるかもしれません。ガウス分布とは「正規分布」と呼ばれる確率分布です。おそらく,学校の実験や業務での実験の統計解析等で下記のようなグラフをみたことあるのではないでしょうか? 下記のグラフは横軸が観測データ,縦軸が確率密度(相対的な出やすさ)をあらわしています。ガウス分布(正規分布)とは,観測データがとりうる観測誤差の確率密度を表す分布となります。このガウス分布に従う観測データでは,平均$\mu$の値がもっとも出やすく,平均値から遠い値ほど観測されづらいということになります。コスト関数のスカラー値$f (K_{P})$における確率密度がこのガウス分布の確率密度に従うとします。
以上の仮定のもと,既知の実験結果からコスト関数の推定を試みます。ベイズ最適化では,ガウス過程という方法にてコスト関数を推定します。ガウス過程とは一言でいうと,「既知の実験結果を用いて,ガウス分布に従う未知関数の出力を平均と標準偏差として推定する」関数を指します。マイルドな言い方に直すと,ガウス過程とは「入力に対する出力を確率的に推定する魔法の箱」です。「どうしてそんなことができるんですか?」という疑問が当然出ると思いますが,それを数式で説明すると本記事の尺がまったく足りないので図を使って雰囲気だけお伝えしておきます。
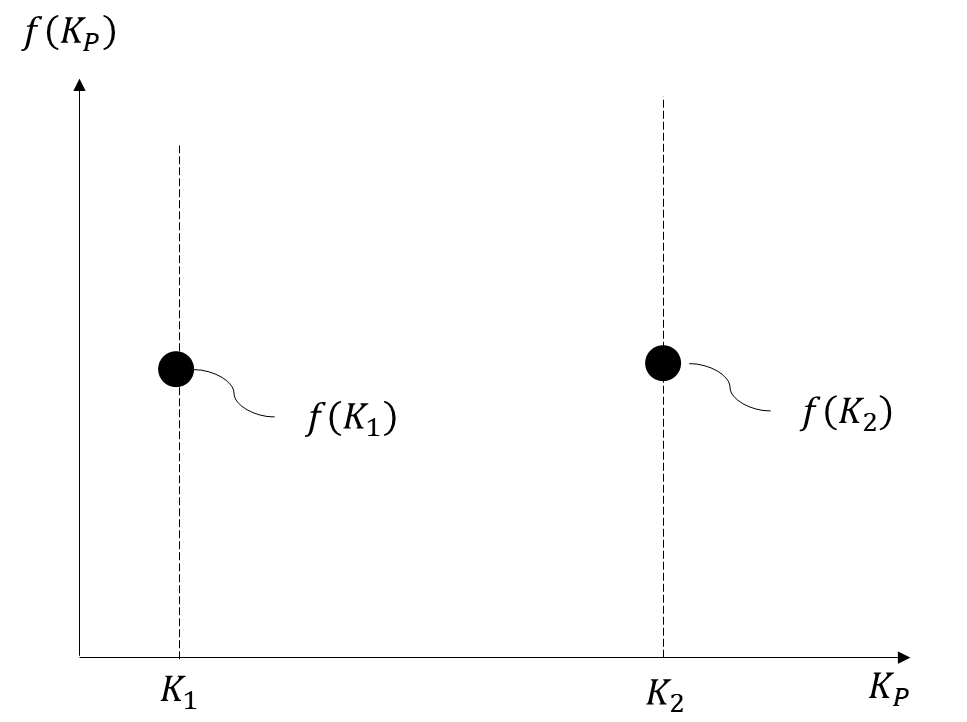
下記に横軸を比例ゲイン,縦軸をコスト関数としたグラフを示します。初期実験で実験済みの$K_{1}$と$K_{2}$に関してはコスト関数のスカラー値である$f(K_1)$と$f(K_2)$が既知なので,下記のようにプロットできます。この2点のデータを使って,コスト関数の比例ゲインに対する挙動を推定してみましょう。
ガウス分布には「ガウス分布に従う関数において,関数への入力が似ていれば関数の出力も似ている」という不思議な特性があります。つまり,上記の図において「$K_{1}$に近い値の比例ゲインを使って実験した場合,$f(K_{1})$に近い値のコスト関数のスカラー値を得られる可能性が高い」ということが成り立ちます。$K_{2}$での実験結果も既知の値となるため,「$K_{2}$に近い値の比例ゲインを使って実験した場合,$f(K_{2})$に近い値のコスト関数のスカラー値を得られる可能性が高い」ということも成り立ちます。これを言い換えると,「$K_{2}$か$K_{1}$に近い値の比例ゲインにおけるコスト関数の値は,標準偏差の小さい推定値として計算できる」「$K_{2}$と$K_{1}$から離れた値の比例ゲインにおけるコスト関数の値は,標準偏差の大きい推定値として計算できる」ということになります。この理屈を利用することにより,既知の実験結果からコスト関数の挙動を推定できます。
ここで新たな疑問として,「ガウス過程によるコスト関数推定の概念はわかったけど,肝心の$\mu$と$\sigma$を定量的にどう計算するの?」と思うかもしれません。$\mu$と$\sigma$の推定には,カーネル関数という関数を使います。カーネル関数を一言で表すと,「入力した二つのサンプルの類似度を共分散として出力する魔法の箱」です。共分散とは相関係数に互いの標準偏差を掛けたものであり,値が正や負に大きいほど相関が高く (似ており),0 に近いほど相関が低い (似ていない) といえます。つまり,サンプル間の類似度のようなものです。このカーネル関数を今回の問題に適用することにより,「実験済みの比例ゲインと未知の比例ゲインの類似度を共分散として出力する」ことができ,任意の比例ゲイン$K_{P}$に対するコスト関数$f(K_{P})$の挙動を平均と分散として推定できます。カーネル関数に関してはだいたいのケースでは,ガウスカーネル
k(K_{P},K'_{P})= \frac{\exp{||K_{P}-K'_{P}||^2}}{2l^2}
を共分散関数として採用することが多いです。$l$はガウスカーネル関数のハイパーパラメータです。カーネル関数の詳細に関しては,下記の記事をご確認いただけると内容がよりわかるかもしれません。
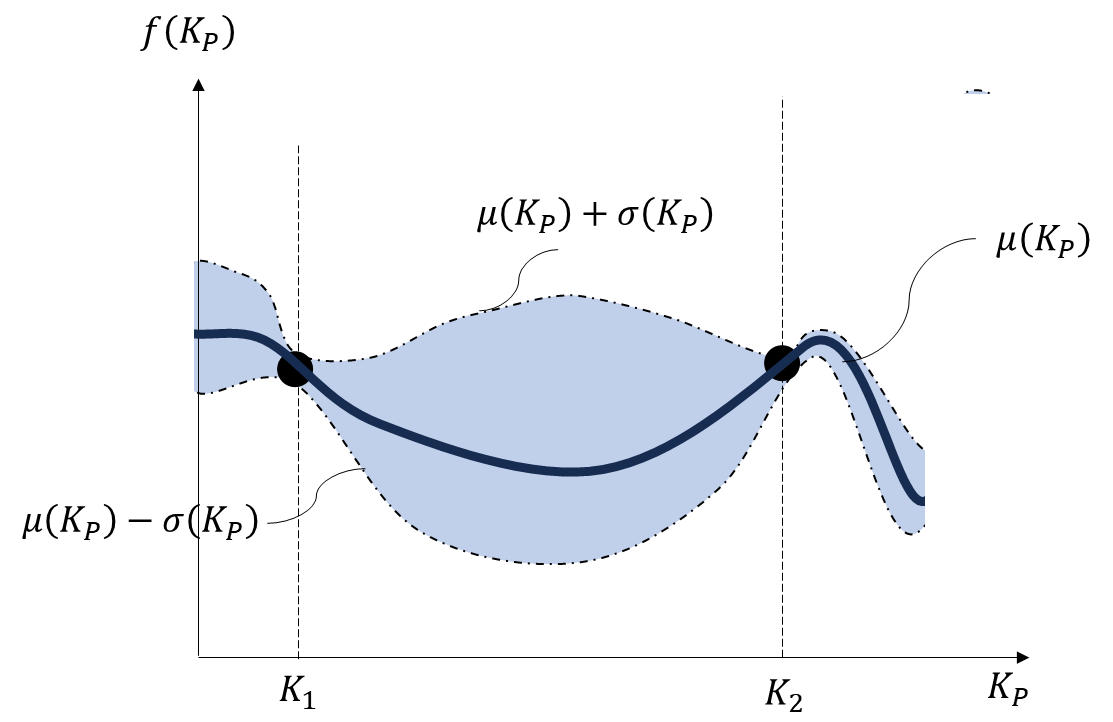
このカーネル関数を使って平均値と標準偏差を既知の実験結果から計算することにより,任意の比例ゲインに対するコスト関数の挙動をFig.4のように推定できます。黒い実線が期待値である平均$\mu(K_{P})$となっています。この実線は既知の実験結果のプロット点を通るような線としてプロットされます。一点鎖線で囲まれている青い部分が不確かさを指しています。一点鎖線$\sigma(K_{P})$の上部分が$\mu(K_{P})+\sigma(K_{P})$であり,下部分が$\mu(K_{P})-\sigma(K_{P})$となります。既知の実験結果のプロット点に近い比例ゲインでの推定値ほど不確かさが小さく,既知の実験結果に遠い比例ゲインほど推定値の不確かさが大きいことがわかります。これがガウス過程によるコスト関数の推定の概念です。コスト関数がガウス分布に従うと仮定することにより,既知の実験結果からコスト関数の挙動を平均と標準偏差として推定できます。
コスト関数を推定できるようになったため,推定結果を用いてコスト関数を最小化するような比例ゲインを調整することを目指します。推定されたコスト関数が確率的なモデルとなっているため,確定モデルにおける数理最適化を用いたパラメータ調整ができません。そこで,ベイズ最適化ではコスト関数の代わりに獲得関数と呼ばれる別の関数を最小(最大)化するようなパラメータ調整を実施します。
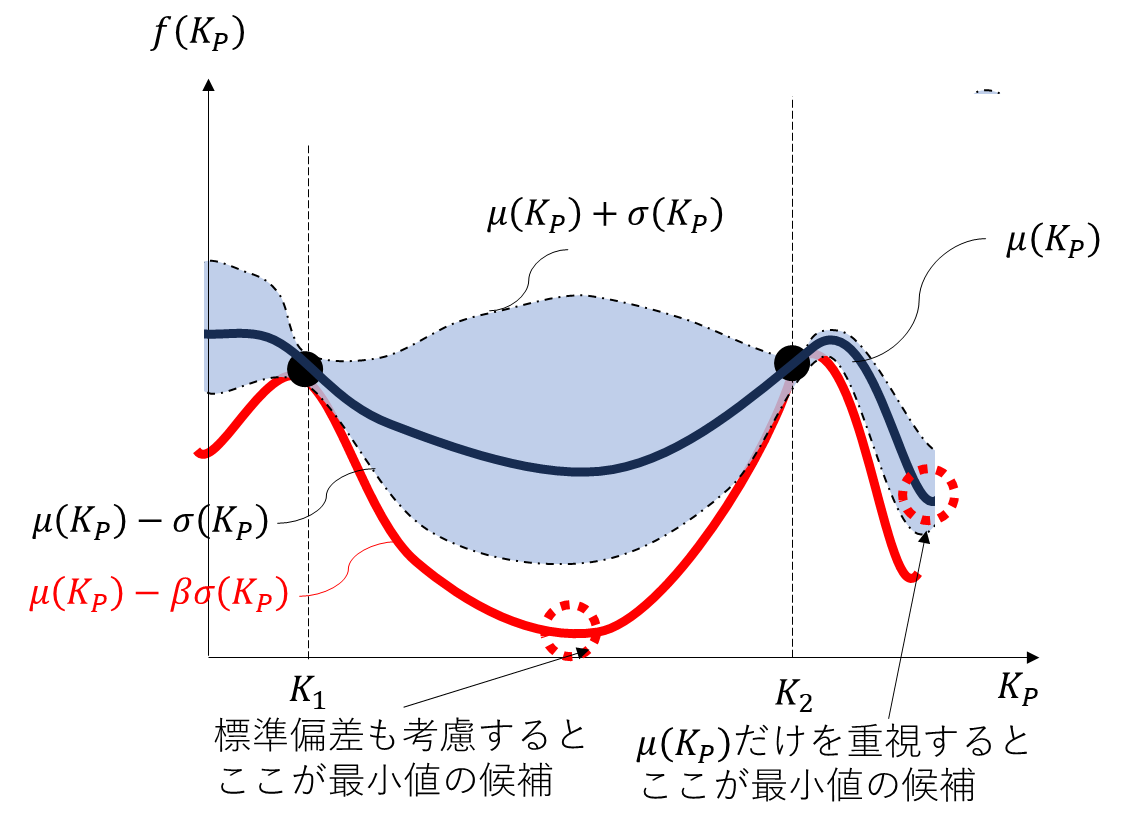
獲得関数にもいくつか種類がありますが,ここでは様々なケースへの適用事例が多いLower confidence boundという関数を使います。Fig.4のコスト関数の推定に関する図を見た際に,みなさんはどのあたりの部分の比例ゲインを選んで実験するでしょうか? 平均値だけをみると,$K_{2}$よりも右側の領域の比例ゲインにて実験すると,コスト関数が小さくするようなゲインが得られるように見えます。一方,$K_{2}$と$K_{1}$の中間値では,コスト関数の推定値における標準偏差が大きいため,コスト関数の返り値を$f(K_{2})$や$f(K_{1})$よりも劇的に削減できるかもしれません。$K_{1}$と$K_{2}$付近のゲインであれば標準偏差が小さいため,コスト関数の返り値を小さくなるようなゲインを見つけられる可能性が高いと思われます。しかしながら,平均値の推定値を鑑みるとコスト関数を劇的に削減するような比例ゲインが求まらない可能性があります。
以上のように,コスト関数の推定値における平均値と標準偏差のトレードオフを考え,バランスのよいパラメータ選定をする必要があります。これがLower confidence boundにおける考え方です。ベイズ最適化では,コスト関数の推定結果における平均$\mu(K_{P})$と標準偏差$\sigma(K_{P})$のどちらを重視してパラメータを選ぶか決めます。具体的には,
a(K_{P})=\mu(K_{P})-\beta \sigma(K_{P})
が最小となるような比例ゲインを選びます。$\beta$がハイパーパラメータとなります。$\beta$を大きくすることにより,標準偏差が大きい区間のパラメータを選びやすくなります。$\beta$を小さくすることにより,平均値が小さい区間のパラメータを選びやすくなります。この獲得関数が小さくなるような比例ゲインを選んでみます。Fig.5のように平均値だけ考えると$K_{2}$よりも大きい比例ゲインを選ぶとよさそうです。ただし,標準偏差まで考慮すると$K_{1}$と$K_{2}$の中間あたりの比例ゲインを選ぶと,獲得関数を小さくするようなゲインが得られるように見えます。
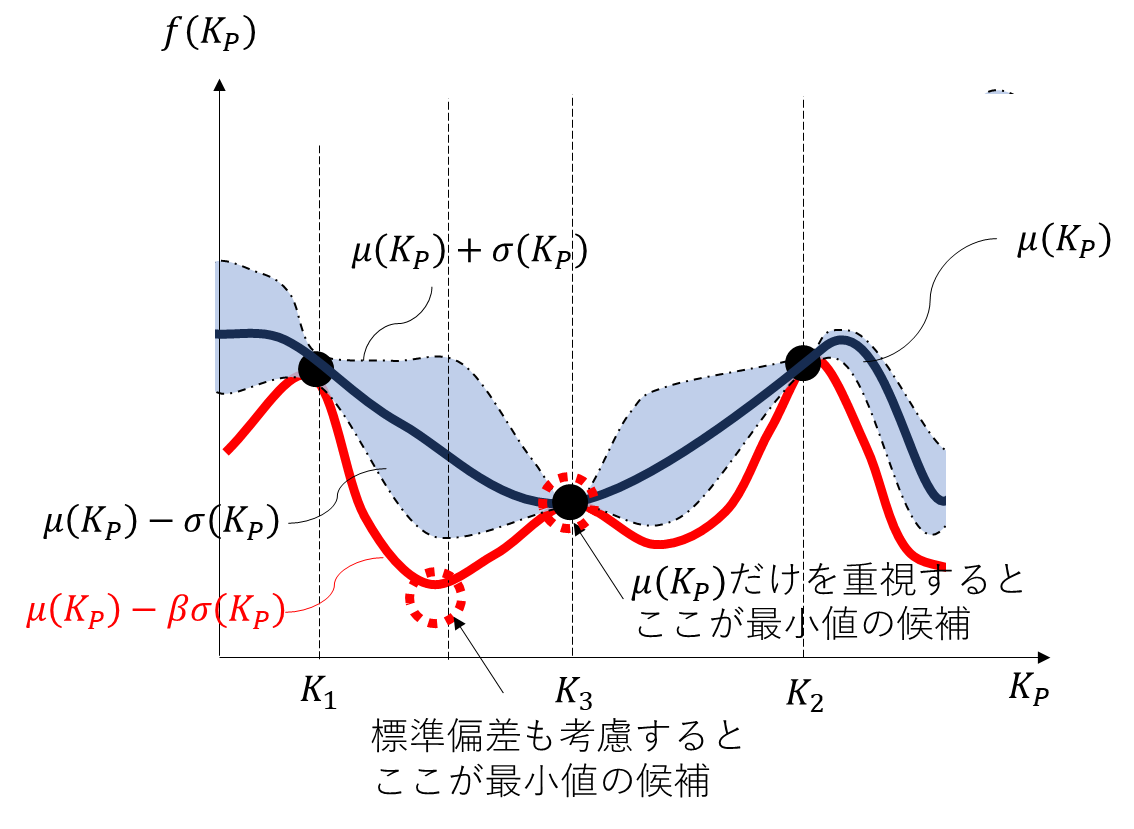
$K_{1}$と$K_{2}$の中間あたりの比例ゲイン$K_{3}$を選んで実験し,実験結果を用いてカーネル関数を更新してコスト関数を再度推定した結果がFig.6のようになったとします。新しい実験結果を得たことにより,平均値と標準偏差の推定結果が変化しています。
再び獲得関数が小さくなるような点を探します。Fig.7で示すように今度は$K_{1}$と$K_{3}$の中間あたりの比例ゲインを選ぶと,獲得関数を小さくするようなゲインが得られるように見えます。
以上のように,既知の実験結果を用いてカーネル関数によるコスト関数の挙動を分散と平均として推定し,獲得関数が小さくなるようなゲインを選びます。選んだゲインにて実験を実施し,新しい実験結果を用いてカーネル関数を更新し,コスト関数の推定を再更新します。そして,再び獲得関数が小さくなるようなゲインを選びます。この手順を所定回数繰り返すことにより,なるべく少ない実験回数にてブラックボックスなコスト関数を最小化する比例ゲインを決定できます。
ベイズ最適化によるパラメータ調整は下記の手順でまとめることができます。
-
初期設定
最大試行回数やカーネル関数・獲得関数の種類などを事前に設定する。また,パラメータ探索の範囲と各関数のハイパーパラメータも事前に設定しておく。 -
初期実験
適当な値の比例ゲイン$K_{1}$を設定して閉ループ実験を実施し,その際のコスト関数のスカラー値$f (K_{1})$を測定する。この実験を複数回繰り返えして,別の値のゲインに対するコスト関数のスカラー値を複数回測定してもよい。 -
コスト関数の推定
既知の結果として,実験済みのn個の比例ゲインのベクトル$K_{P}’=[K_{1}, K_{2},...K_{n}]^T$と実験にて取得したコスト関数のスカラー値のベクトル$f’ (K_{P}’)=[f (K_{1}), f (K_{2}),...f (K_{n})]^T)$を定義する。パラメータ探索範囲における任意の比例ゲイン$K_{P}$に対するコスト関数$f (K_{P})$をカーネル関数を用いたガウス過程回帰で推定する。 -
獲得関数の最小化
手順3)で推定したコスト関数$f (K_{P})$を用いて,$K_{P}$でパラメタライズされた獲得関数の出力を計算する。 -
実験
手順4)で計算した獲得関数を最小化する比例ゲインを設定して閉ループ実験し,コスト関数のスカラー値を取得する。 -
データの更新
新たに取得した比例ゲインとコスト関数のスカラー値を用いて,比例ゲインのベクトル$K_{P}’=[K_{1}, K_{2},...K_{n}]^T$と実験にて取得したコスト関数のスカラー値のベクトル$f’ (K_{P}’)=[f (K_{1}), f (K_{2}),...f (K_{n})]^T)$を更新する。 -
繰り返し
最大試行回数に到達するまで手順3)から6)までを繰り返す。
今回は読者の理解を深めるために比例制御を例として挙げましたが,これがPIDゲインの調整になっても理屈としては同じです。1次元ガウス分布による推定とパラメータ調整を多次元のガウス分布の問題へ拡張することで,PIDゲインをベイズ最適化の手順で調整できます。
PIDゲインの三つのパラメータを調整する場合においても,既知の実験結果を用いたガウス過程によるコスト関数推定を実施し,推定したコスト関数による推定結果に基づいて獲得関数が最小化するようなパラメータを探索します。以上がベイズ最適化のよるパラメータ調整の手順です。
注意事項
ここではベイズ最適化によるいくつかの注意事項に関して説明していきます。すべての点に関して言及できませんが,可能な範囲で読者が参考となるような注意点を記載しておきます。
カーネル関数と獲得関数の選定について
今回の記事では,ベイズ最適化におけるカーネル関数をガウスカーネルに設定しました。一方,実際には問題設定や対象に応じたカーネル関数を設定する必要があります。もしガウスカーネルにて適切なパラメータが求まらない場合,対象の事前知識をもとに適切なカーネル関数を選定する必要があります。例えば,北九州市立大学の藤本先生の研究グループの方では,制御系設計に適したカーネル関数の選定に関する研究が報告されています。必ずしも,今回の記事で紹介したガウスカーネルが適切なカーネル関数となるわけでないことにご注意ください。
参考文献:
佐藤宏樹, & 藤本悠介. (2022). ベイズ最適化による制御器パラメータ調整のためのカーネル関数. 計測自動制御学会論文集, 58(11), 505-511.
獲得関数選定に関しても,本記事で紹介したLower confidence bound以外にも様々な関数が提案されています。獲得関数の選定には推奨の方法があるわけでなく,問題設定によって適切な方法が異なります。今回用いたLower confidence boundは,序盤は標準偏差が大きい箇所を中心にパラメータを選定し,最終的に既知の実験結果付近の最小値を見つけることができます。コスト関数における複数の極小値に囚われることなく大域的な最小値を見つけることに向いているため,著者としてはよく使う方法として紹介させていただきました。
適用可能な制御器に関して
今回の記事では,制御屋さんの皆さんにベイズ最適化の理屈を理解していただくため,比例制御器を例題として取り上げて解説をさせていただきました。前章の末尾でも説明しましたが,ベイズ最適化によるパラメータ調整に関してはPID制御のパラメータ調整にも活用できます。事例として,下記の研究論文においてPIDゲイン調整にベイズ最適化を活用した事例が紹介されています。
参考文献:
中野雄一郎, 藤本悠介, & 杉江俊治. (2019). ベイズ最適化を用いた制御器チューニング—提案と実験検証—. 計測自動制御学会論文集, 55(4), 269-274.
また,ベイズ最適化は出力フィードバック制御器の調整のみでなく,状態フィードバック制御やオブザーバのパラメータ調整にも適用できます。例えば,下記の論文では状態フィードバック制御のLQRの重み調整にベイズ最適化を適用した事例が報告されています(Twitter(X)でとある方からご紹介いただきました)。
参考文献:
Miyamoto, K., She, J., Sato, D., & Yasuo, N. (2018). Automatic determination of LQR weighting matrices for active structural control. Engineering Structures, 174, 308-321.
下記の計測自動制御学会の英文雑誌の方では,オブザーバ設計時のリカッチ代数方程式の重みをベイズ最適化にて自動設計する手法が報告されています。
参考文献:
Yahagi, S., & Suzuki, M. (2023). Intelligent PI control based on the ultra-local model and Kalman filter for vehicle yaw-rate control. SICE Journal of Control, Measurement, and System Integration, 16(1), 38-47.
以上のように,様々な制御系にベイズ最適化によるパラメータ調整を適用できることがわかります。一方,ベイズ最適化も万能な方法でないため,適用が難しい制御対象もあります。ベイズ最適化に限定した話ではありませんが,多数のパラメータを同時に調整するような方法に不向きといわれています。可調整パラメータが大量に存在するような制御系の場合,ベイズ最適化によるパラメータ調整では収束しないことが考えられます。PID制御や状態フィードバック制御程度のパラメータ数では問題ありませんが,Lookup tableを用いた制御のような可調整パラメータが非常に膨大となる制御系にベイズ最適化を適用する場合は注意してください。
事前実験・ハイパーパラメータに関して
ベイズ最適化によるパラメータ調整では,パラメータ探索範囲の設定と事前実験が必要です。他の数理最適化にも共通しますが,パラメータ探索範囲内に最適解が存在しなければ,いくらパラメータ探索してもコスト関数を減らすようなパラメータを得ることができません。一方,パラメータ探索範囲が広すぎると,最大試行回数以内に最適化計算が収束しないことがあります。探索範囲に関しては,制御対象や制御器の事前情報を上手く活用して事前に適切な範囲を設定しておきましょう。事前実験に関しても,適切な実験結果を事前に取得しておくことが推奨されます。ベイズ最適化におけるLower confidence boundにてパラメータ調整する場合,既知の実験結果をもとにコスト関数を推定します。もし,パラメータの探索範囲内をある程度網羅するような事前実験結果が得られていれば,なるべく少ない実験回数にてより最小値に近いパラメータを得ることが期待できます。
例題
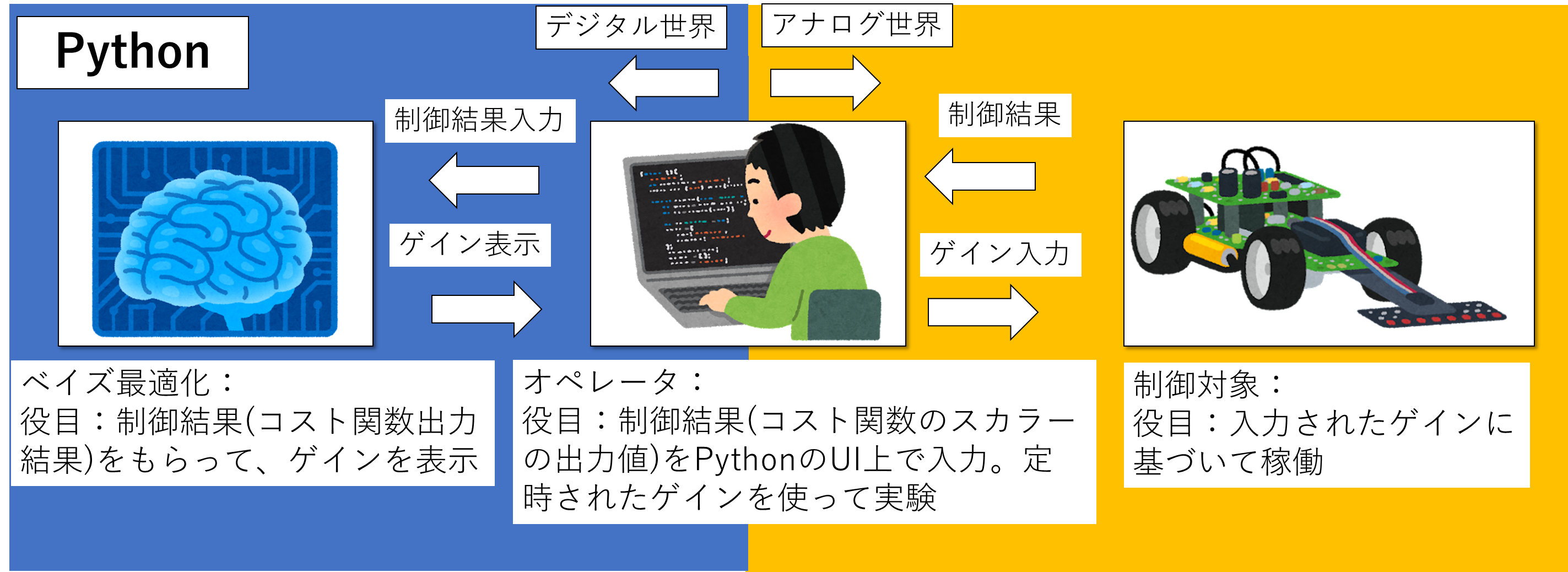
それではサンプルプログラムを通して,実際にパラメータ調整を体感してみましょう。今回はベイズ最適化による実験を実施することを想定し,Fig.8のようなシチュエーションに対応したサンプルプログラムをPythonで作成しました。ベイズ最適化のゲイン計算プログラムを使ってオペレータ(実験者)がゲインを調整することを想定しています。オペレータの役割として,PythonのUI上に表示されたゲインを実験システムに入力して制御対象を稼働させます。実験によって得られた制御結果(実験結果から求めたコスト関数の返り値)をオペレータがPythonのUIを介してベイズ最適化のソフトへ入力することにより,繰り返しのゲイン計算と実験を実施できます。このようなシステムをつくることにより,オペレータの技量に依存せずに制御系のパラメータチューニングができるようになります。オペレータが制御工学に詳しいエンジニアである必要もなくなり,人件費削減や作業員の属人化を解消することが期待できます。
なお,今回の例題ではGpyoptライブラリの関数を使用してベイズ最適化を実施します。Pythonのソフトに関しては本記事の末尾に記載しておきます。ご興味あればぜひご確認ください。
例題1
早速サンプルプログラムを用いて実験をやっていきましょう。現実世界の実機を用いてやっていきたいところですが,読者が手軽に再現検証できるよう伝達関数の数学モデルを制御対象としておきます。簡単な例として次の対象に対するパラメータ調整問題を考えてみましょう。制御対象の伝達関数を
P=\frac{1}{s^{2}+2s+1}
と設定します。また,制御器を一般的なPID制御器:
C=K_{P}
としました。目標値として,単位ステップ信号を設定します。オペレータ目線では,制御対象の特性が未知であり,どのようなゲインを設定すべきかがわかりません。オペレータにできることは,ゲインを実験システムに与えてコスト関数の返り値を計算することだけです。以上の問題設定のもと,ベイズ最適化にゲインを調整することを目指しましょう。ここではコスト関数として
f (K_{P})=\lambda \max(\Delta y(kT_{s}),0)+\sum_{k=0}^{N}(y(kT_{s},K_{P})-r(kT_{s}))^2
を設定します。右辺第一項はオーバーシュートに関する罰則項です。$\lambda$が罰則項の定数重みであり,適当な大きい値にしておけば問題ないです。$\max(\Delta y(kT_{s}),0)$はオーバーシュートが発生した際に,オーバーシュート量に$\lambda$をかけて返り値として返すmax関数です。オーバーシュートしない場合,$\max(\Delta y(kT_{s}),0)=0$となります。コスト関数の重みを$\lambda$=100としました。このコスト関数の設定により,ベイズ最適化にて比例ゲインを調整します。
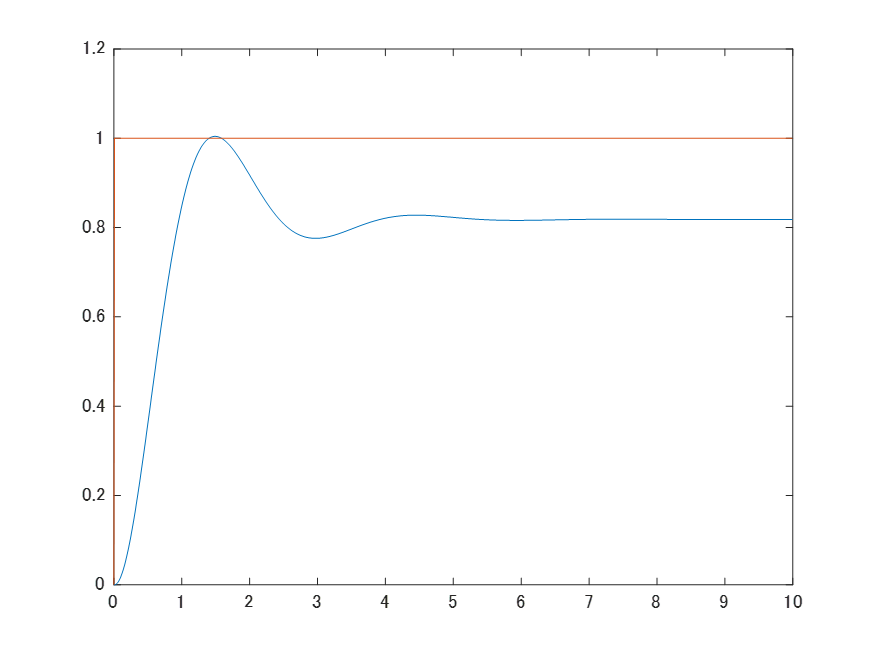
初期実験では,ランダムなゲインを設定して実験し,その後10回程度の試行回数でベイズ最適化によるゲイン調整を実施しました。パラメータの探索範囲を0~10の区間に設定しました。パラメータ探索の刻み幅は0.1としています。ベイズ最適化によるゲイン調整を実施した結果,10回の試行回数にて$K_{P}$=4.5の比例ゲインを得られました。調整後ゲインにて検証した結果が下記のグラフです。青線が出力,橙線が目標値となります。過剰なオーバーシュートを発生させずに目標値と出力の偏差がなるべく小さくなるような制御結果となっております。ベイズ最適化により,比例制御のゲインを調整できることがわかりました。
例題2
例題1では制御器が比例制御器でした。制御対象に積分特性が含まれていないため,比例制御だと内部モデル原理により定常偏差が0となりません。定常偏差が0となるようなフィードバック制御を実現する場合,制御器に積分器を含める必要があります,そこで,制御器を一般的なPID制御器:
C=K_{P}+\frac{K_{I}}{s}+K_{D}{s}
としました。それ以外の問題設定は例題1のままとします。コスト関数も例題1と同じです。可調整パラメータを$\rho=[K_{P},K_{I},K_{D}]^T$として
f (\rho)=\lambda \max(\Delta y(kT_{s}),0)+\sum_{k=0}^{N}(y(kT_{s},\rho)-r(kT_{s}))^2
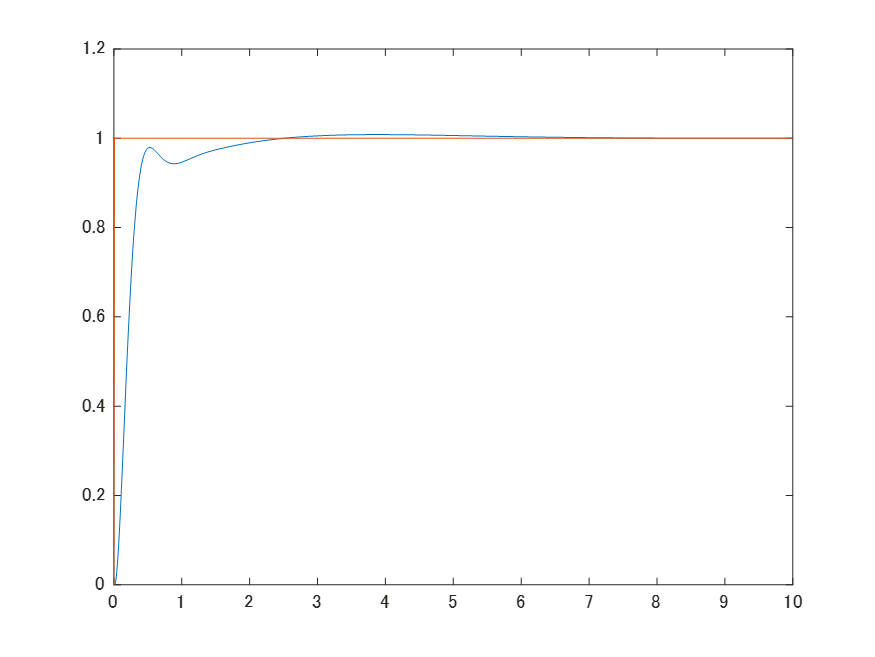
をコスト関数に設定しました。パラメータの探索範囲を0~10の区間に設定しました。パラメータ探索の刻み幅は0.1としています。以上の条件のもと,PIDゲインを調整します。ベイズ最適化によるゲイン調整を実施した結果,15回の試行回数にて$K_{P}$=7.5,$K_{I}$=4.4,$K_{D}$=5.4のゲインを得られました。調整後ゲインにて検証した結果が下記のグラフです。青線が出力,橙線が目標値となります。過剰なオーバーシュートを発生させずに目標値と出力の偏差がなるべく小さくなるような制御結果となっております。内部モデル原理により定常偏差も0となっていることがわかります。以上の結果から,PIDゲインをベイズ最適化にて調整できることを確認できました。余談ですが,今回は制御系にノイズを印加していないため、微分ゲインの値が高めに調整されました。現実の制御対象にベイズ最適化を適用する場合,ノイズの影響で微分ゲインが小さめに調整されるハズなのでご注意ください。
まとめ
本記事では制御系設計にベイズ最適化を上手く活用していただくことを目指し,なるべく数式を使わずに理論の簡単な部分の解説をしました。本記事がベイズ最適化を使った制御系の入門となれば幸いです。今回は制御屋さんにとってなじみ深いフィードバック制御器の設計を例題に取り上げ,ベイズ最適化の厳密な数式の厳密な説明・記載を意図的に省略して説明しました。もし機会があれば,厳密な理屈の深堀やより難しい例題での効果検証なども取り組んでみたいと思います。
サンプルコード
下記にPythonのベイズ最適化によるサンプルコードを記載しておきます。2024/04/29時点でのGoogle colabで動作確認済みのため,もしご興味あれば参考にしてみてください。
# ベイズ最適化プログラム(GpyOpt版 実験用)
# 事前実験無し版
# 作成日2022/11/23
# 更新日2024/04/29
!pip install gpyopt
import numpy as np
from matplotlib import pyplot as plt
import pandas as pd
import GPyOpt
import warnings
warnings.filterwarnings('ignore') #警告を非表示
# 評価関数の定義
def f(x):
kp, ki, kd = x[:,0], x[:,1], x[:,2]
print("next kp =", kp, "next ki =", ki, "next kd =", kd)
score = float(input("Input J : "))
return score
# 最適化するパラメータの下限・上限
# 探索範囲が広すぎると収束に時間必要
xx_p=np.arange(0,10,0.1)
xx_i=np.arange(0,10,0.1)
xx_d=np.arange(0,10,0.1)
bounds = [{'name': 'kp', 'type': 'discrete', 'domain': xx_p},{'name': 'ki', 'type': 'discrete', 'domain': xx_i},{'name': 'kd', 'type': 'discrete', 'domain': xx_d}]
my_bopt=GPyOpt.methods.BayesianOptimization(f=f,domain=bounds,initial_design_numdata=1,acquisition_type='LCB',acquisition_weight=2) #LCB
my_bopt.run_optimization(max_iter=17) #パラメータ探索
# 以下ゲイン表示処理
kp=my_bopt.x_opt[0]
ki=my_bopt.x_opt[1]
kd=my_bopt.x_opt[2]
print(my_bopt.x_opt)
print(my_bopt.fx_opt)
my_bopt.plot_acquisition()
my_bopt.plot_convergence()