Retro*とは
Retro*とは2020年にBinghong Chenらが開発したニューラルネットワークを活用した逆合成解析ツールです(https://arxiv.org/abs/2006.15820)。有機化学において目的の生成物を合成するために必要な反応試薬や触媒、適切な反応条件を決定することは極めて重要です。逆合成解析とはこの目的化合物を効率よく合成するための一連の反応を導き出す作業になります。Retro*ではニューラルネットワークを活用したA*探索アルゴリズムをベースに逆合成解析を効率的に行う方法を提案しています。
目的
本記事ではこのRetro*の原理を解析・理解し、0から予測から学習までを動かすことができるようになることを目標とします。
細かい情報は公式GitHubにも載っていますが、ここでは補足を加えて解説し、動かし方を説明します。
Retro*を使って逆合成経路を予測してみる
ます、Retro*を実装し、実際にRetro*を使って逆合成経路を予測してみました。Retro*は次のコードによって与えた化合物の逆合成経路を予測します。
サンプルコード
from retro_star.api import RSPlanner
planner = RSPlanner(
gpu=-1,
use_value_fn=True,
iterations=100,
expansion_topk=50
)
result = planner.plan('CCCC[C@@H](C(=O)N1CCC[C@H]1C(=O)O)[C@@H](F)C(=O)OC')
まず、Retro*のGitHubに例として挙げられている上記のコードを実行しましたが、逆合成ルートが見つかりませんでした。
そこで次にtargetの化合物をCCOC(=O)c1nc(N2CC[C@H](NC(=O)c3nc(C(F)(F)F)c(CC)[nH]3)[C@H](OC)C2)sc1Cに変えて実行したところ逆合成ルートが見つかり、次の出力得られました。
{
'succ': True,
'time': 4.271811246871948,
'iter': 7,
'routes': 'CCOC(=O)c1nc(N2CC[C@H](NC(=O)c3nc(C(F)(F)F)c(CC)[nH]3)[C@H](OC)C2)sc1C>0.0010>CCc1[nH]c(C(=O)N[C@H]2CCN(C(=O)OC(C)(C)C)C[C@H]2OC)nc1C(F)(F)F.CCOC(=O)c1nc(Br)sc1C|CCc1[nH]c(C(=O)N[C@H]2CCN(C(=O)OC(C)(C)C)C[C@H]2OC)nc1C(F)(F)F>0.9998>CCc1[nH]c(C(=O)O)nc1C(F)(F)F.CO[C@@H]1CN(C(=O)OC(C)(C)C)CC[C@@H]1N|CCc1[nH]c(C(=O)O)nc1C(F)(F)F>0.9916>CCc1[nH]c(C=O)nc1C(F)(F)F.[O-][Cl+][O-]|CCc1[nH]c(C=O)nc1C(F)(F)F>0.9994>CCc1[nH]c(C(OC)OC)nc1C(F)(F)F|CCc1[nH]c(C(OC)OC)nc1C(F)(F)F>1.0000>O=C1CCC(=O)N1Cl.COC(C=O)OC.CCC1(C(=O)C(F)(F)F)SCCCS1.N|CCC1(C(=O)C(F)(F)F)SCCCS1>1.0000>CCC1SCCCS1.CCOC(=O)C(F)(F)F',
'route_cost': 6.905857713253809,
'route_len': 6
}
この出力はそれぞれ'succ'は逆合成探索が成功したかどうか、'time'は探索に要した時間(秒)、'iter'は探索に用いたイテレーションの数、'routes'は逆合成ルート、'route_cost'はこのルートでの逆合成に必要なコスト、'route_len'は逆合成ルートの長さを示しています。実際にこのルートを構造式に起こして見てみると次のようになります。
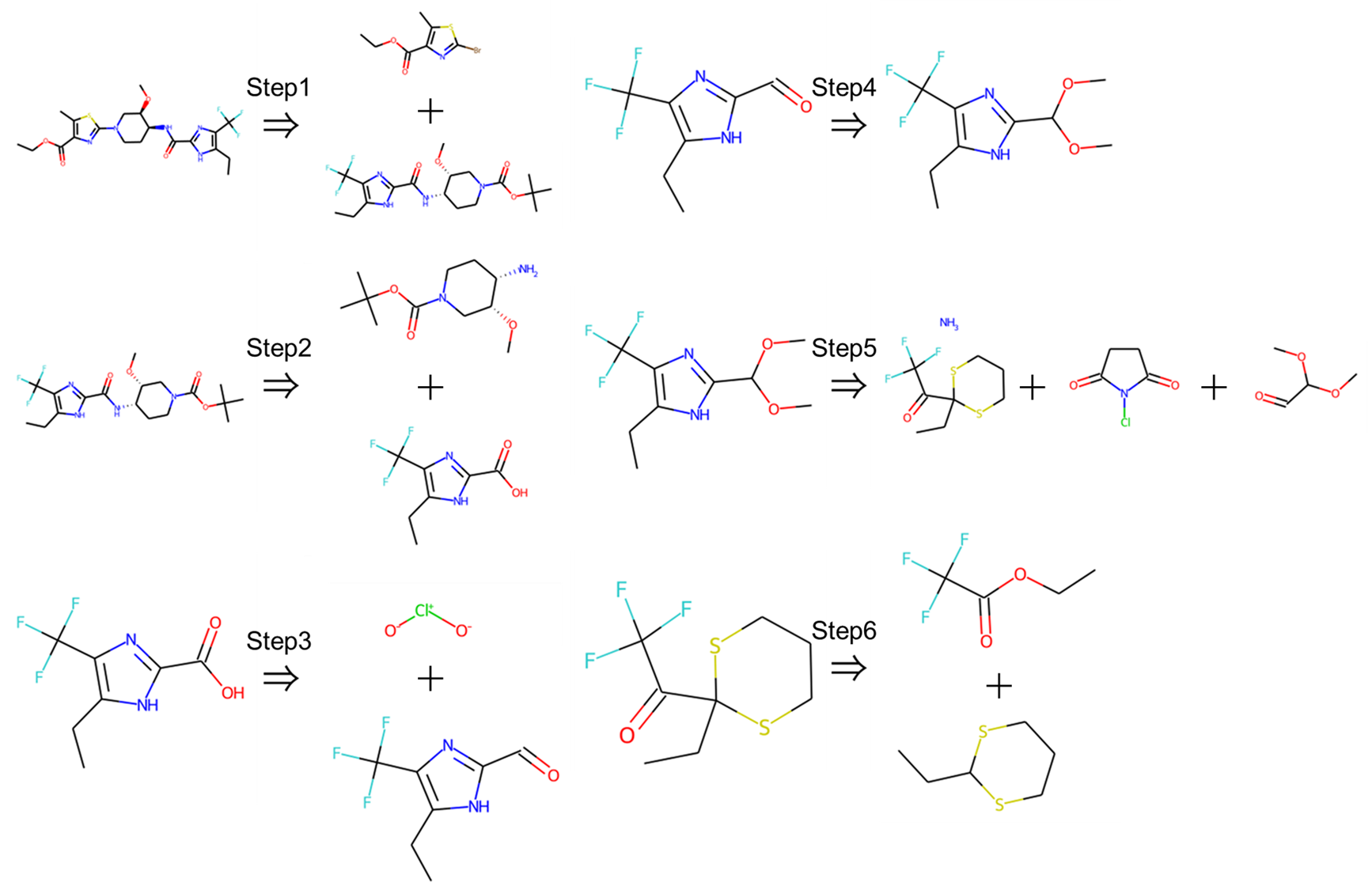
このように市販されているレベルの単純な化合物まで遡り反応ルートを構築できていることがわかります。
しかし、最初の例のように逆合成ルートを導き出せないものもいくつか存在します。そのため、使用の目的によってはさらに多くの反応を学習させたりする必要や、導き出す反応の条件を変更する必要が出てくるかもしれません。そこで、本記事ではその助けになるようRetro*の原理を解析・理解し、0から新たな反応を学習させることを目標としています。
Retro*を理解する
Retro*を0から動かすことを目標に、コードひとつひとつ確認しながらRetro*の理解を深めます。
予測経路を探索するRSPlanner
まず、予測経路を探索するRSPlannerクラスについてみてみます。
RSPlanner
class RSPlanner:
def __init__(self,...):
...
starting_mols = prepare_starting_molecules(starting_molecules)
one_step = prepare_mlp(mlp_templates, mlp_model_dump)
if use_value_fn:
model = ValueMLP(...)
...
model.eval()
def value_fn(mol):
fp = smiles_to_fp(mol, fp_dim=fp_dim).reshape(1, -1)
fp = torch.FloatTensor(fp).to(device)
v = model(fp).item()
return v
else:
value_fn = lambda x: 0.
self.plan_handle = prepare_molstar_planner(
one_step=one_step,
value_fn=value_fn,
starting_mols=starting_mols,
expansion_topk=expansion_topk,
iterations=iterations,
viz=viz,
viz_dir=viz_dir
)
def plan(self, target_mol):
t0 = time.time()
succ, msg = self.plan_handle(target_mol)
if succ:
result = {
'succ': succ,
'time': time.time() - t0,
'iter': msg[1],
'routes': msg[0].serialize(),
'route_cost': msg[0].total_cost,
'route_len': msg[0].length
}
return result
else:
logging.info('Synthesis path for %s not found. Please try increasing '
'the number of iterations.' % target_mol)
return None
RSPlannerクラスは次の5つの関数によって駆動されています。
1. prepare_starting_molecules
これは逆合成解析においてゴールとなる入手可能な化合物のSMILESを指定したファイルから読み込む関数です。csv形式もしくはpkl形式でまとめられた化合物群を読み込みます。Retro*においては出発物質となる化合物はdataset/origin_dict.csvにまとめられています。
この化合物群を追加・変更することで、出発物質の幅を広げたりすることができます。
2. prepare_mlp
1段階反応を予測するニューラルネットワークMLPモデルを読み込む関数です。入力された分子に対してそれを合成可能な反応の候補を出力する関数one_stepを出力します。1段階反応を予測するMLPモデルについての詳細は後述します。
3. value_fn
反応経路の評価を行う関数です。ValueMLPモデルを利用して各反応ステップにおける化合物にスコアを与えます。このスコアはその化合物を合成するコストを表しており、このスコアを利用して最短経路を導き出します。ValueMLPモデルについての詳細は後述します。
4. prepare_molstar_planner
合成経路探索エンジンであるmolstarを分子を指定するだけで合成経路を探索できるようにするplan_handleを作成する関数です。これにより、ユーザーはplan_handle(target_mol)を実行するだけで、Retro*による分子の合成経路を探索ができるようになります。molstarについての詳細は後述します。
5. plan
逆合成予測を行うRSPlannerクラスの逆合成経路探索の実行本体部分となっている関数です。先述したように実際にRetro*を使用する際はplanner.plan(SMILES)の形でこの関数を呼び出し、逆合成解析を行います。メソッドの中ではplan_handleを用いて逆合成解析を行ない、その出力から適切な逆合成経路が見つかれば、辞書型の出力として逆合成経路が提示されます。
{
'succ': True, # 成功したかどうか
'time': X.XX # 探索にかかった時間(秒)
'iter': XX, # 探索にかかったイテレーション数
'routes': {...}, # 逆合成ルート
'route_cost': X.XX, # 逆合成ルート全体のコストの合計(小さいほど良い)
'route_len': X # ルートの長さ(反応ステップ数)
}
もし探索がうまくいかず、逆合成ルートが見つからない場合はその旨がメッセージにより出力されます。
目的の逆合経路が見つからなかった場合はiterationsを増やす、starting_molsの幅を広げるなどの手段をとると良いかもしれません。
1段階反応を予測するMLPモデル
続いて、ある化合物を合成するため1段階の反応を予測するone_stepのニューラルネットワークであるMLPモデルについてみてみます。MLPとはMulti Layer Perceptron(多層パーセプトロン)の略で複数の中間層を持つ機械学習手法の1つです。
Retro*で使われているMLPModelクラスは次のようになっています。
MLPModel
class MLPModel(object):
def __init__(self,state_path, template_path, device=-1, fp_dim=2048):
...
def run(self, x, topk=10):
arr = preprocess(x, self.fp_dim)
arr = np.reshape(arr,[-1, arr.shape[0]])
arr = torch.tensor(arr, dtype=torch.float32)
if self.device >= 0:
arr = arr.to(self.device)
preds = self.net(arr)
preds = F.softmax(preds,dim=1)
if self.device >= 0:
preds = preds.cpu()
probs, idx = torch.topk(preds,k=topk)
rule_k = [self.idx2rules[id] for id in idx[0].numpy().tolist()]
reactants = []
scores = []
templates = []
for i , rule in enumerate(rule_k):
out1 = []
try:
out1 = rdchiralRunText(rule, x)
if len(out1) == 0: continue
out1 = sorted(out1)
for reactant in out1:
reactants.append(reactant)
scores.append(probs[0][i].item()/len(out1))
templates.append(rule)
except ValueError:
pass
if len(reactants) == 0: return None
reactants_d = defaultdict(list)
for r, s, t in zip(reactants, scores, templates):
if '.' in r:
str_list = sorted(r.strip().split('.'))
reactants_d['.'.join(str_list)].append((s, t))
else:
reactants_d[r].append((s, t))
reactants, scores, templates = merge(reactants_d)
total = sum(scores)
scores = [s / total for s in scores]
return {'reactants':reactants,
'scores' : scores,
'template' : templates}
このクラスの中で予測を行っているのはrun関数であり、その関数の中で与えられた化合物xをpreprocessによりfingerprint(arr)に変換し、これを使って学習済みMLPモデルを通して反応テンプレートを予測しスコアを得ます。そして、softmax関数によりスコアを確率に変換し、確率が高い順に与えられたtopK個分のテンプレート(rule)を取り出します。
続いて逆合成反応を疑似的に行う関数であるrdchiralRunTextが化合物xとテンプレートを入力とし、その反応における出発物質となる反応物(reactants)を出力します。この際、予測したテンプレートの確率(softmax確率)を反応物の数で割った値をその反応のスコアとして定義しています。そして、得られた反応物ごとにスコアとテンプレートを整理し、それらをまとめた辞書を返します。この時、スコアについては反応物の重複がある場合はすべての反応のスコアの合計を新たなスコアとするため、再正規化が行われています。また、返り値となる辞書の中では反応物やスコア、テンプレートはmerge関数により、反応物のスコアの高い順に並び替えられています。
候補化合物を評価するValueMLP
次に、反応経路途中の化合物の評価を行う関数value_fnのモデルである。ValueMLPについてみてみます。
これはフィンガープリント(fps)を入力として、その化合物の合成にかかるコスト予測を行う多層パーセプトロン(MLP)モデルです。
Retro*においては次のようなクラスとして定義されています。
ValueMLP
class ValueMLP(nn.Module):
def __init__(self, n_layers, fp_dim, latent_dim, dropout_rate, device):
...
logging.info('Initializing value model: latent_dim=%d' % self.latent_dim)
layers = []
layers.append(nn.Linear(fp_dim, latent_dim))
layers.append(nn.ReLU())
layers.append(nn.Dropout(self.dropout_rate))
for _ in range(self.n_layers - 1):
layers.append(nn.Linear(latent_dim, latent_dim))
layers.append(nn.ReLU())
layers.append(nn.Dropout(self.dropout_rate))
layers.append(nn.Linear(latent_dim, 1))
self.layers = nn.Sequential(*layers)
def forward(self, fps):
x = fps
x = self.layers(x)
x = torch.log(1 + torch.exp(x))
return x
このようにValueMLPはn_layersで指定した数のLinear層->ReLU層->Dropout層を繰り返し、最後に出力サイズが1になるようにLinear層に通し、出力を反応を評価する価値(Value)として扱うためsoftplus関数(log(1 + exp(x)))を用いて出力を0以上の連続値への変換しています。
ValueMLPは次のTrainerクラスを用いて学習されます。
Trainer
class Trainer:
def __init__(self, model, train_data_loader, val_data_loader, n_epochs, lr,
save_epoch_int, model_folder, device):
...
self.optim = optim.Adam(
filter(lambda p: p.requires_grad, self.model.parameters()),
lr=lr
)
def _pass(self, data, train=True):
self.optim.zero_grad()
for i in range(len(data)):
data[i] = data[i].to(self.device)
fps, values, r_costs, t_values, r_fps, r_masks = data
v_pred = self.model(fps)
loss = F.mse_loss(v_pred, values)
batch_size, n_reactants, fp_dim = r_fps.shape
r_values = self.model(r_fps.view(-1, fp_dim)).view((batch_size,
n_reactants))
r_values = r_values * r_masks
r_values = torch.sum(r_values, dim=1, keepdim=True)
r_gap = - r_values - r_costs + t_values + 7.
r_gap = torch.clamp(r_gap, min=0)
loss += (r_gap**2).mean()
if train:
loss.backward()
self.optim.step()
return loss.item()
def _train_epoch(self):
self.model.train()
losses = []
pbar = tqdm(self.train_data_loader)
for data in pbar:
loss = self._pass(data)
losses.append(loss)
pbar.set_description('[loss: %f]' % (loss))
return np.array(losses).mean()
def _val_epoch(self):
self.model.eval()
losses = []
pbar = tqdm(self.val_data_loader)
for data in pbar:
loss = self._pass(data, train=False)
losses.append(loss)
pbar.set_description('[loss: %f]' % (loss))
return np.array(losses).mean()
def train(self):
best_val_loss = np.inf
for epoch in range(self.n_epochs):
self.train_data_loader.reshuffle()
train_loss = self._train_epoch()
val_loss = self._val_epoch()
logging.info(
'[Epoch %d/%d] [training loss: %f] [validation loss: %f]' %
(epoch, self.n_epochs, train_loss, val_loss)
)
if (epoch + 1) % self.save_epoch_int == 0:
save_file = self.model_folder + '/epoch_%d.pt' % epoch
torch.save(self.model.state_dict(), save_file)
上記の学習コードでは、正例(fps)と負例(r_fps)をそれぞれモデルに通し、正例では予測と正解の価値(Value)の誤差(MSE)が小さくなるように学習し、負例では生成物の価値(Value)より十分小さくなるように学習させています。この反応コストは1段階反応予測のMLPモデルによって計算されるスコアをもとに計算されます。(負の対数尤度)これにより誤った反応経路で高い価値(Value)を与え、誤った反応経路を選択しないようにしています。
合成経路探索エンジンmolstar
最後に、Retro*において与えられた分子から合成経路探索を実行するmolstarについてみてみます。
molstarは以下のような関数として定義されます。
molstar
def molstar(target_mol, target_mol_id, starting_mols, expand_fn, value_fn,
iterations, viz=False, viz_dir=None):
mol_tree = MolTree(
target_mol=target_mol,
known_mols=starting_mols,
value_fn=value_fn
)
i = -1
if not mol_tree.succ:
for i in range(iterations):
scores = []
for m in mol_tree.mol_nodes:
if m.open:
scores.append(m.v_target())
else:
scores.append(np.inf)
scores = np.array(scores)
if np.min(scores) == np.inf:
logging.info('No open nodes!')
break
metric = scores
mol_tree.search_status = np.min(metric)
m_next = mol_tree.mol_nodes[np.argmin(metric)]
assert m_next.open
result = expand_fn(m_next.mol)
if result is not None and (len(result['scores']) > 0):
reactants = result['reactants']
scores = result['scores']
costs = 0.0 - np.log(np.clip(np.array(scores), 1e-3, 1.0))
# costs = 1.0 - np.array(scores)
if 'templates' in result.keys():
templates = result['templates']
else:
templates = result['template']
reactant_lists = []
for j in range(len(scores)):
reactant_list = list(set(reactants[j].split('.')))
reactant_lists.append(reactant_list)
assert m_next.open
succ = mol_tree.expand(m_next, reactant_lists, costs, templates)
if succ:
break
# found optimal route
if mol_tree.root.succ_value <= mol_tree.search_status:
break
else:
mol_tree.expand(m_next, None, None, None)
logging.info('Expansion fails on %s!' % m_next.mol)
logging.info('Final search status | success value | iter: %s | %s | %d'
% (str(mol_tree.search_status), str(mol_tree.root.succ_value), i+1))
best_route = None
if mol_tree.succ:
best_route = mol_tree.get_best_route()
assert best_route is not None
if viz:
if not os.path.exists(viz_dir):
os.makedirs(viz_dir)
if mol_tree.succ:
if best_route.optimal:
f = '%s/mol_%d_route_optimal' % (viz_dir, target_mol_id)
else:
f = '%s/mol_%d_route' % (viz_dir, target_mol_id)
best_route.viz_route(f)
f = '%s/mol_%d_search_tree' % (viz_dir, target_mol_id)
mol_tree.viz_search_tree(f)
return mol_tree.succ, (best_route, i+1)
molstarはMolTreeと呼ばれる探索木を反復的に展開することで合成経路を探索します。
MolTreeは出発分子に相当する分子ノードから反応テンプレートに基づいた逆合成反応に相当する反応ノードを展開し、さらにその逆合成の結果生成されるいくつかの分子ノードが新たに形成します。このようにMolTreeは分子ノード->反応ノード->分子ノード->...というノードが繰り返されるツリー構造(AND-OR木)を形成します。
molstarでは次の流れに従ってMolTreeを展開し、逆合成経路を探索します。
-
MolTreeの初期化
MolTreeは初期化時に与えられた出発分子に対応する分子ノードを作成し、これが逆合成経路探索の出発点となります。 -
MolTreeの展開
mol_tree.succがTrueになる、もしくは次の条件に達するまでMolTreeによる探索を繰り返す
2-1. 展開可能なノードが存在しない
2-2. すでに見つかっている探索ルートの'scc_value'より、'search_status'が高くなる
2-3. 指定した反復回数'iterations'に達する - 最適な逆合成経路の探索
mol_tree.succがTrueになった場合、見つかった候補ルートの中から最良のルートを探索します。 - Treeの可視化
viz=Trueの場合ルートを可視化します。 - 探索結果の出力
このような流れに沿ってmolstarはstarting_molsとして与えられた既知の分子にたどりつくように探索木を展開します。
また、2のMolTreeによる探索において、先に紹介した1段階反応を予測するMLPモデル(onestep)と候補反応を評価するValueMLP(value_fn)はその中核となる重要な働きを担っています。
onestepはMolTreeにおいてexpand_fnとして定義され、与えらた分子(分子ノード)に対して、適応可能な逆合成のテンプレートを予測し、疑似的な逆合成を行うことで1段階前の反応基質(reactants)を出力します。この結果に基づき、molstarではMolTreeに新たな反応ノードと分子ノードを構築していきます。
そして、ValueMLP(value_fn)は各分子ノードにおいて、それぞれの分子の合成コストを予測します。そして、この値が反応経路を選ぶ際の基準となり、コストの低いものから反応経路の探索が行われます。そして全体の反応を通じてこのコストの合計の最も低いものが最適な経路として導き出されます。
Retro*を学習させる①~MLPモデル
ここまでで、Retro*の逆合成経路予測の仕組みや流れを解説したので、まずは、逆合成経路予測の肝となるMLPモデル(onestep)の学習を0から行い、新たに構築したモデルを用いたRetro*を使って逆合成経路予測を行ってみます。
MLPモデルは、ある生成物に対して、どの逆合成ルートを適用すべきかを予測するモデルになります。
既存のRetro*ではUSPTOのデータセットが学習に用いられていますが、今回は練習のために別の反応データセットを使います。具体的には、学習用データセットとしてORDのデータセットを用い、簡単のためその中から750個の反応のみを利用してRetro*の学習、および学習したモデルの評価を行います。
まず、学習を行うコードを確認し学習に必要なデータの準備を行います。
MLPモデルを学習するためのコードは次のようになっています。
mlp_train
import os
from collections import defaultdict
from tqdm import tqdm
from mlp_policies import train_mlp
from pprint import pprint
if __name__ == '__main__':
import argparse
parser = argparse.ArgumentParser(description="train function for retrosynthesis Planner policies")
parser.add_argument('--template_path',default= 'data/cooked_data/templates.dat',
type=str, help='Specify the path of the template.data')
parser.add_argument('--template_rule_path', default='data/cooked_data/template_rules_1.dat',
type=str, help='Specify the path of all template rules.')
parser.add_argument('--model_dump_folder',default='./model',
type=str, help='specify where to save the trained models')
parser.add_argument('--fp_dim',default=2048, type=int,
help="specify the fingerprint feature dimension")
parser.add_argument('--batch_size', default=1024, type=int,
help="specify the batch size")
parser.add_argument('--dropout_rate', default=0.4, type=float,
help="specify the dropout rate")
parser.add_argument('--learning_rate', default=0.001, type=float,
help="specify the learning rate")
args = parser.parse_args()
template_path = args.template_path
template_rule_path = args.template_rule_path
model_dump_folder = args.model_dump_folder
fp_dim = args.fp_dim
batch_size = args.batch_size
dropout_rate = args.dropout_rate
lr = args.learning_rate
print('Loading data...')
prod_to_rules = defaultdict(set)
### read the template data.
with open(template_path, 'r') as f:
for l in tqdm(f, desc="reading the mapping from prod to rules"):
rule, prod = l.strip().split('\t')
prod_to_rules[prod].add(rule)
if not os.path.exists(model_dump_folder):
os.mkdir(model_dump_folder)
print(args)
train_mlp(prod_to_rules,
template_rule_path,
fp_dim=fp_dim,
batch_size=batch_size,
lr=lr,
dropout_rate=dropout_rate,
saved_model=os.path.join(model_dump_folder, 'saved_rollout_state_1'))
このコードでは以下の2つのファイルを使用しています。
- 反応のテンプレートファイル(
templates.dat) - テンプレートのルールファイル(
template_rules_1.dat)
これらのファイルの詳細は記述されていませんが、ソースコードから解釈すると、いかに記述する内容で用意すれば学習できることがわかります。
学習に必要な2つのファイルの準備
1. 反応のテンプレートファイル
こちらのファイルは化学反応をSMIRKSという表現で書かれた反応テンプレートと生成物の原子マッピングされたSMILESが入っています。SMIRKSとはSMILESとSMRATSを合わせたような表現で、化学反応を前後の分子を「>>」でつなぎ表現します。そして、反応の前後で同じ原子は同じ番号でマッピングされ、結合が変化するところはSMILES、結合が変化しないところはSMARTSで表現されます。詳しくはこちらの記事を参考にしてください。
[NH2;D1;+0:1]-[c:2]>>O=[N+;H0;D3:1](-[O-])-[c:2] [Cl:1][C:2]1[N:3]=[CH:4][C:5]2[C:10]([CH:11]=1)=[C:9]([NH2:12])[CH:8]=[CH:7][CH:6]=2
[C:5]-[O;H0;D2;+0:6]-[S;H0;D4;+0:1](-[C:2])(=[O;D1;H0:3])=[O;D1;H0:4]>>Cl-[S;H0;D4;+0:1](-[C:2])(=[O;D1;H0:3])=[O;D1;H0:4].[C:5]-[OH;D1;+0:6] [CH2:5]([S:7]([O:4][CH2:3][CH2:2][Br:1])(=[O:9])=[O:8])[CH3:6]
[C:2]-[S;H0;D4;+0:1](=[O;D1;H0:3])(=[O;D1;H0:4])-[O;H0;D2;+0:6]-[C:5]>>Cl-[S;H0;D4;+0:1](-[C:2])(=[O;D1;H0:3])=[O;D1;H0:4].[C:5]-[OH;D1;+0:6] [CH2:10]([S:14]([O:3][CH2:2][CH2:1][Cl:4])(=[O:16])=[O:15])[CH:11]([CH3:13])[CH3:12]
2. テンプレートのルールファイル
こちらのファイルは反応のSMIRKSのみが記載されています。
[NH2;D1;+0:1]-[c:2]>>O=[N+;H0;D3:1](-[O-])-[c:2]
[C:5]-[O;H0;D2;+0:6]-[S;H0;D4;+0:1](-[C:2])(=[O;D1;H0:3])=[O;D1;H0:4]>>Cl-[S;H0;D4;+0:1](-[C:2])(=[O;D1;H0:3])=[O;D1;H0:4].[C:5]-[OH;D1;+0:6]
[C:2]-[S;H0;D4;+0:1](=[O;D1;H0:3])(=[O;D1;H0:4])-[O;H0;D2;+0:6]-[C:5]>>Cl-[S;H0;D4;+0:1](-[C:2])(=[O;D1;H0:3])=[O;D1;H0:4].[C:5]-[OH;D1;+0:6]
[C:5]-[O;H0;D2;+0:6]-[S;H0;D4;+0:1](-[C;D1;H3:2])(=[O;D1;H0:3])=[O;D1;H0:4]>>Cl-[S;H0;D4;+0:1](-[C;D1;H3:2])(=[O;D1;H0:3])=[O;D1;H0:4].[C:5]-[OH;D1;+0:6]
これらのファイルを作るためにORDから200個のユニークなPRODUCTを与える反応を抽出し、extract_template.py(retro_star/retro_star/packages/mlp_retrosyn/mlp_retrosyn/extract_template.py)を使って新たなtemplates.datとtemplate_rules_1.datを作成しました。
extract_template.pyのコードは次のようになっています。
extract_template.py
if __name__ == '__main__':
import argparse
from pprint import pprint
parser = argparse.ArgumentParser(description="Policies for retrosynthesis Planner")
parser.add_argument('--data_folder', default='../data/uspto_all/',
type=str, help='Specify the path of all template rules.')
parser.add_argument('--file_name',default='proc_all_cano_smiles_w_tmpl.csv',
type=str,
help='Specify the filen name')
args = parser.parse_args()
data_folder = args.data_folder
file_name = args.file_name
templates = defaultdict(tuple)
transforms = []
datafile = os.path.join(data_folder,file_name)
df = pd.read_csv(datafile)
rxn_smiles = list(df['rxn_smiles'])
retro_templates = list(df['retro_templates'])
for i in tqdm(range(len(df))):
rxn = rxn_smiles[i]
rule = retro_templates[i]
product = rxn.strip().split('>')[-1]
transforms.append((rule,product))
print(len(transforms))
with open(os.path.join(data_folder,'templates.dat'), 'w') as f:
f.write('\n'.join(['\t'.join(rxn_prod) for rxn_prod in transforms]))
# Generate rules for MCTS
templates = defaultdict(int)
for rule, _ in tqdm(transforms):
templates[rule] += 1
print("The number of templates is {}".format(len(templates)))
# #
template_rules = [rule for rule, cnt in templates.items() if cnt >= 1]
print("all template rules with count >= 1: ", len(template_rules))
with open(os.path.join(data_folder,'template_rules_1.dat'), 'w') as f:
f.write('\n'.join(template_rules))
こちらのコードは、引数として各反応の必要な情報の入ったCSVファイルが入っているのフォルダへのパス(--data_folder)とCSVファイルのファイル名(--file_name)を受け取り、CSVファイルの入っているフォルダ内に、templates.datとtemplate_rules_1.datを作成します。
このとき、入力に必要な各反応の必要な情報の入ったCSVファイルは、id, rxn_smiles, retro_templates, cano_rxn_smilesの列を持つファイルであり各列にはそれぞれ、idの列には各反応の番号、rxn_smilesの列には原子マッピングされたReaction SMILES、retro_templatesの列には各反応のSMIRKS、そしてcano_rxn_smilesの列にはカノニカル化されたReaction SMILESのデータが入っています。
そのため、templates.datとtemplate_rules_1.datを作成するためには、それぞれ、原子マッピングにはRXNMapperを、SMIRKSの生成にはextract_from_reaction(retro_star/retro_star/packages/rdchiral/rdchiral/template_extractor.py)を用い、次のコードにより、ORDから抽出したSMILESのリストから、各反応の必要な情報の入ったCSVファイルを作成する必要があります。
SMILES_to_SMIRKS
from rxnmapper import RXNMapper
from rdchiral.template_extractor import extract_from_reaction
from rdkit import Chem
import pandas as pd
import pickle
def make_canonical_smiles(df):
rxn_list = []
for index, row in df.iterrows():
prod_smiles = row['product_smiles']
prod_mol = Chem.MolFromSmiles(prod_smiles)
canonical_prod = Chem.MolToSmiles(prod_mol)
react_list = []
for i in range(6):
smiles = row[f'smiles{i}']
if smiles != None:
mol = Chem.MolFromSmiles(smiles)
if mol != None:
react_list.append(Chem.MolToSmiles(mol))
canonical_react = '.'.join(react_list)
rxn_smiles = canonical_react + '>>' + prod_smiles
rxn_list.append(rxn_smiles)
return rxn_list
rxn_mapper = RXNMapper()
def rxn_smiles_to_smirks(canonicl_rxn_smiles):
mapped = rxn_mapper.get_attention_guided_atom_maps([canonicl_rxn_smiles])
mapped_rxn = mapped[0]['mapped_rxn'] # → アトムマップ付きReaction SMILES
# 分割(reactants >> products の形式)
reactants, products = mapped_rxn.split('>>')
# rdchiral に渡す dict 構造
reaction = {
'_id': 0, # 必須キーなので適当なIDを付与
'reactants': reactants,
'products': products
}
# SMIRKS を抽出
template_info = extract_from_reaction(reaction)
SMIRKS_temp = template_info['reaction_smarts']
return canonicl_rxn_smiles, mapped_rxn, SMIRKS_temp
with open('data/ord/ord_reaction-sortdata0.pkl', 'rb') as f:
ord_data = pickle.load(f)
rxn_list = make_canonical_smiles(ord_data)
ids = []
rxn_smiles = []
mapps = []
temps = []
for i, canonicl_rxn_smiles in zip(ord_data['internal_id'], rxn_list):
canonicl_rxn_smiles, mapped_rxn, SMIRKS_temp = rxn_smiles_to_smirks(canonicl_rxn_smiles)
ids.append(i)
rxn_smiles.append(canonicl_rxn_smiles)
mapps.append(mapped_rxn)
temps.append(SMIRKS_temp)
dataset = pd.DataFrame({'id':ids, 'rxn_smiles':mapps, 'retro_templates': temps, 'cano_rxn_smiles': rxn_smiles})
dataset.to_csv('data/ord/ord_all_data.csv')
unique_dataset = dataset.drop_duplicates(subset=['retro_templates'])
unique_dataset[0:100].to_csv('data/ord/ord_uique_data100.csv')
このコードでは、まず、事前に用意していたORDのデータセットを読み込みます。このデータセットはORDから読み込んだ750個の反応を含み、生成物のSMILESとその反応物を生成物との類似度をタニモト係数で評価し、生成物に類似しているものから並べたもの、そしてその反応物の収率がまとめられています。
そして、make_canonical_smiles関数により、そのデータセットを入力とし、生成物と6番目までの反応物をそれぞれカノニカル化したSMILESに変換し、「>>」でつないだReaction SMILESのリストを受け取ります。(本来Reaction SMILESは「出発物>反応試薬>生成物」のように表記しますが、今回は出発物と反応試薬をまとめて出発物とし、「出発物>>生成物」の形で表記しています。)
その後、rxn_smiles_to_smirks関数を用いて、それぞれのReaction SMILESを入力とし、カノニカル化したReaction SMILES(canonicl_rxn_smiles)、SMILSから原子マッピングされたReaction SMILES(mapped_rxn)、反応のSMIRKS(SMIRKS_temp)を出力として受けとり、それらをデータフレームに格納します。
最後に、このデータセットの中から同じSMIRKSをもつ反応を削除し、必要な100個の反応をCSVファイルに保存することで、extract_template.pyで必要な各反応の必要な情報の入ったCSVファイルを作成しています。(ここで100個の反応ではなく、ほかの反応を指定することもできるが、mlp_train.pyではTop50のaccuracyを計算しているため、最低でも50個のユニークなSMIRKSが必要になります。)
これにより、extract_template.pyの実行に必要なファイルはそろったので、templates.datとtemplate_rules_1.datを作成します。
!python extract_template.py --data_folder './data/ord/' --file_name 'ord_uique_data100.csv'
追加で必要となるファイルの準備とコードの変更
これにより、学習に必要な2つのファイルがそろったため、mlp_train.pyにより、MLPモデルを学習させようと試みたのですが、次のエラーが発生してしまいました。
FileNotFoundError: [Errno 2] No such file or directory: ‘../data/uspto_all/proc_train_cano_smiles_w_tmpl.csv‘
このエラーは、mlp_train.pyが参照している。mlp_policies.py内で発生しており、該当するファイルが存在していないため発生していました。
そこで、新たにproc_train_cano_smiles_w_tmpl.csv及び、proc_valid_cano_smiles_w_tmpl.csvに相当するファイルを作成する必要がありました。
これらのファイルはMLPモデルの学習に必要なtraining/testデータに相当し、学習に用いる生成物を含む原子マッピングされたReaction SMILESと、ラベルに該当するその反応の逆合成テンプレート(SMIRKS)が必要になります。
そこで、今回は使用したテンプレートデータの作成に利用したORDデータセットを再び利用し、先ほどと同様の流れで、Reaction SMILESとSMIRKSを作成し、学習データとしました。
SMILES_to_SMIRKS
from sklearn.model_selection import train_test_split
with open('data/ord/ord_reaction-sortdata0.pkl', 'rb') as f:
ord_data = pickle.load(f)
rxn_list = make_canonical_smiles(ord_data)
ids = []
rxn_smiles = []
temps = []
for i, canonicl_rxn_smiles in zip(ord_data['internal_id'], rxn_list):
canonicl_rxn_smiles, mapped_rxn, SMIRKS_temp = rxn_smiles_to_smirks(canonicl_rxn_smiles)
ids.append(i)
rxn_smiles.append(canonicl_rxn_smiles)
temps.append(SMIRKS_temp)
dataset = pd.DataFrame({'id':ids, 'rxn_smiles':rxn_smiles, 'retro_templates': temps})
df_train_val, df_test = train_test_split(dataset, test_size=0.1, random_state=42)
df_train, df_val = train_test_split(df_train_val, test_size=0.1, random_state=42)
df_train.to_csv('data/ord/proc_train_cano_smiles_w_tmpl.csv')
df_val.to_csv('data/ord/proc_test_cano_smiles_w_tmpl.csv')
df_test.to_csv('data/ord/ord_test_data.csv')
ここで、proc_train_cano_smiles_w_tmpl.csvとproc_test_cano_smiles_w_tmpl.csvはそれぞれ、学習に用いる学習(train)データと検証(validation)データであり、ord_test_data.csvはモデル評価用データとして保存しています。
このようにして作成した学習・検証データをmlp_policies.pyで使えるように指定したいのですが、ここで用いる学習データのpathはmlp_policies.py内に直接明記されているため、以下のコードのようにtrain_pahtとtest_pathの部分を変更する必要があります。
mlp_policies.py
...
rollout = RolloutPolicyNet(n_rules=len(template_rules),fp_dim=fp_dim,dropout_rate=dropout_rate)
print('num_template_rules:', len(template_rules))
print('mlp model training...')
#train_path = '../data/uspto_all/proc_train_cano_smiles_w_tmpl.csv' <-元のコード
#test_path = '../data/uspto_all/proc_test_cano_smiles_w_tmpl.csv' <-元のコード
train_path = './data/ord/proc_train_cano_smiles_w_tmpl.csv'
test_path = './data/ord/proc_test_cano_smiles_w_tmpl.csv'
X_train, y_train = load_csv(train_path, prod_to_rules, template_rules)
...
MLPモデルの学習
学習・検証データを作成・指定できたため、改めてMLPモデルの学習を行います。
!python mlp_train.py \
--template_path './data/ord/templates.dat' \
--template_rule_path './data/ord/template_rules_1.dat' \
--model_dump_folder './data/ord/'
学習が完了すると、--model_dump_folderで指定したディレクトリにsaved_rollout_state_1_2048_XXXX-XX-XX_XX:XX:XX.ckptのように最良精度を記録したモデルが.ckpt 形式で保存されます。
学習済みMLPモデルの検証
こうして作成したモデルやテンプレートをRSPlannerのmlp_model_dumpやmlp_templatesとして指定し、新たに学習したMLPモデルを用いたRetro*を実行し、その性能を評価しました。
planner = RSPlanner(
gpu=-1,
use_value_fn=True,
mlp_templates=dirpath+'/retro_star/packages/mlp_retrosyn/mlp_retrosyn/data/ord/template_rules_1.dat',
mlp_model_dump=dirpath+'/retro_star/packages/mlp_retrosyn/mlp_retrosyn/data/ord/saved_rollout_state_1_2048_2025-07-14_17:47:53.ckpt',
iterations=100,
expansion_topk=50
)
result = planner.plan('CCOC(=O)c1nc(N2CC[C@H](NC(=O)c3nc(C(F)(F)F)c(CC)[nH]3)[C@H](OC)C2)sc1C')
print(result)
まず、最初に試したのと同様のSMILES(CCOC(=O)c1nc(N2CC[C@H](NC(=O)c3nc(C(F)(F)F)c(CC)[nH]3)[C@H](OC)C2)sc1C)を用いて逆合成予測を行いましたが、イテレーション数が上限に達し、逆合成経路は予測できませんでした。
続いて、学習データ作成時に作成した、学習に用いたORDデータに含まれる分子を用いて作成したモデル評価用データを使って逆合成予測を行いました。その結果、評価用データ中の75個の反応のうち50個(6割以上)の反応において逆合成経路を予測することができました。
これらの予測された逆合成経路を見てみると、少なくとも出発物質に関して
ORDに記載されている反応を用いた合成経路を出力できていることがわかりました。
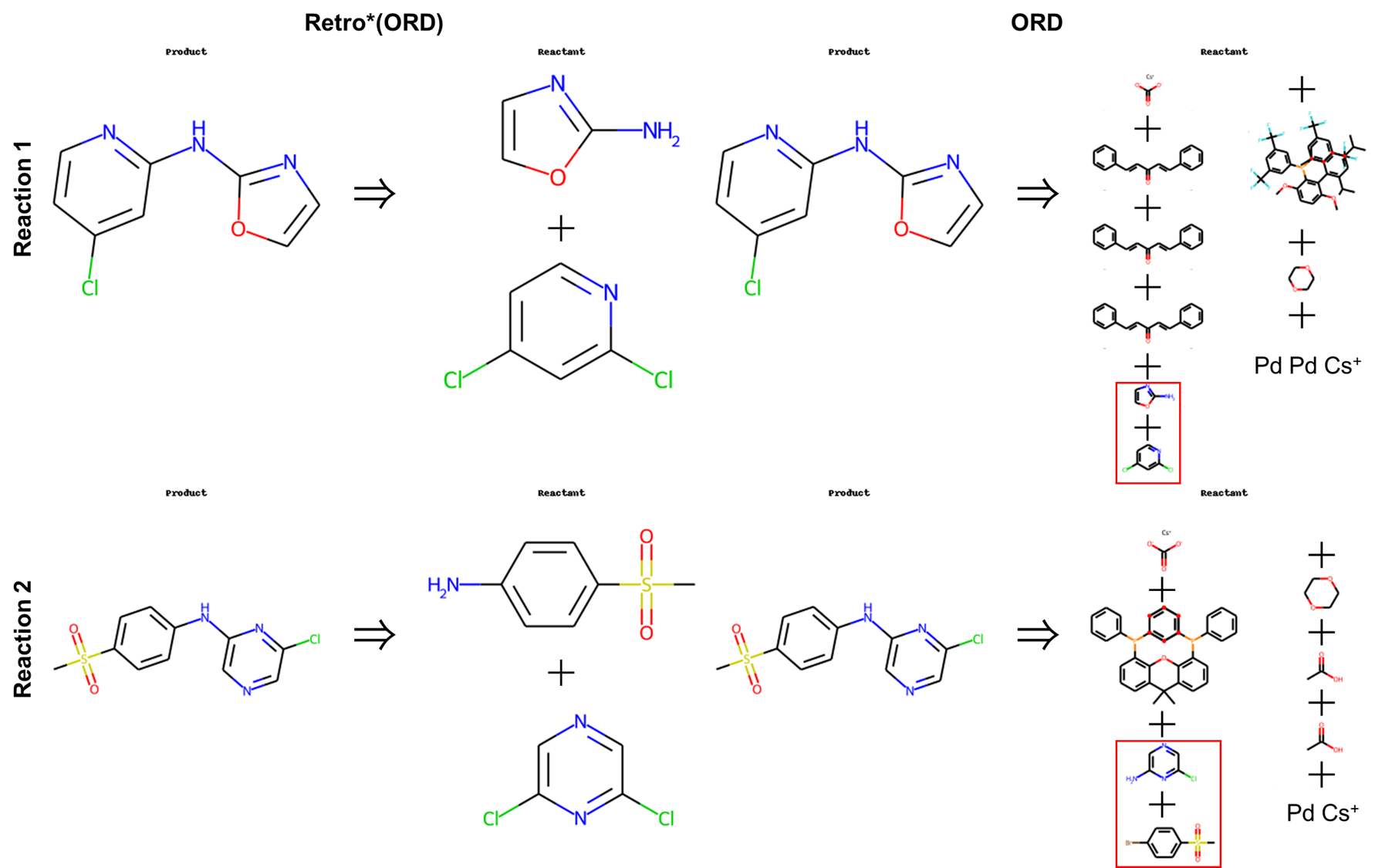
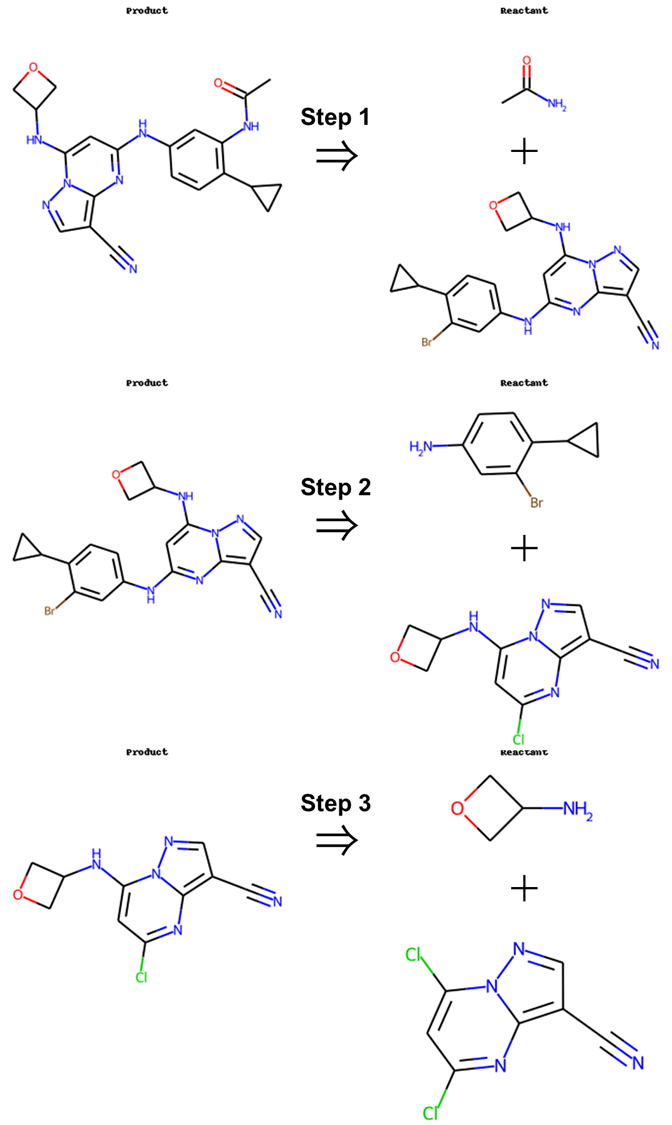
また、ORDは1ステップ反応しか記載されていませんが、今回作成したRetro*では、出発物質がまとめられているorigin_dict.csvに記載がある化合物まで遡って複数ステップのが逆合成経路も導きだせることがわかりました。
予測できなかった反応に対する考察
逆合成経路が予測できなかった残りの25個の反応について、予測ができなった原因を探るため、まず既存のUSPTOのデータセットを用いて学習されたRetro*を使って同じ反応を予測してみました。その結果、すべての反応を予測することができました。
今回の新たにORDのデータセットを用いて学習したRetro*で予測できた結果と比較してみると、ほぼ同じ出発物質を予測できていることがわかりました。
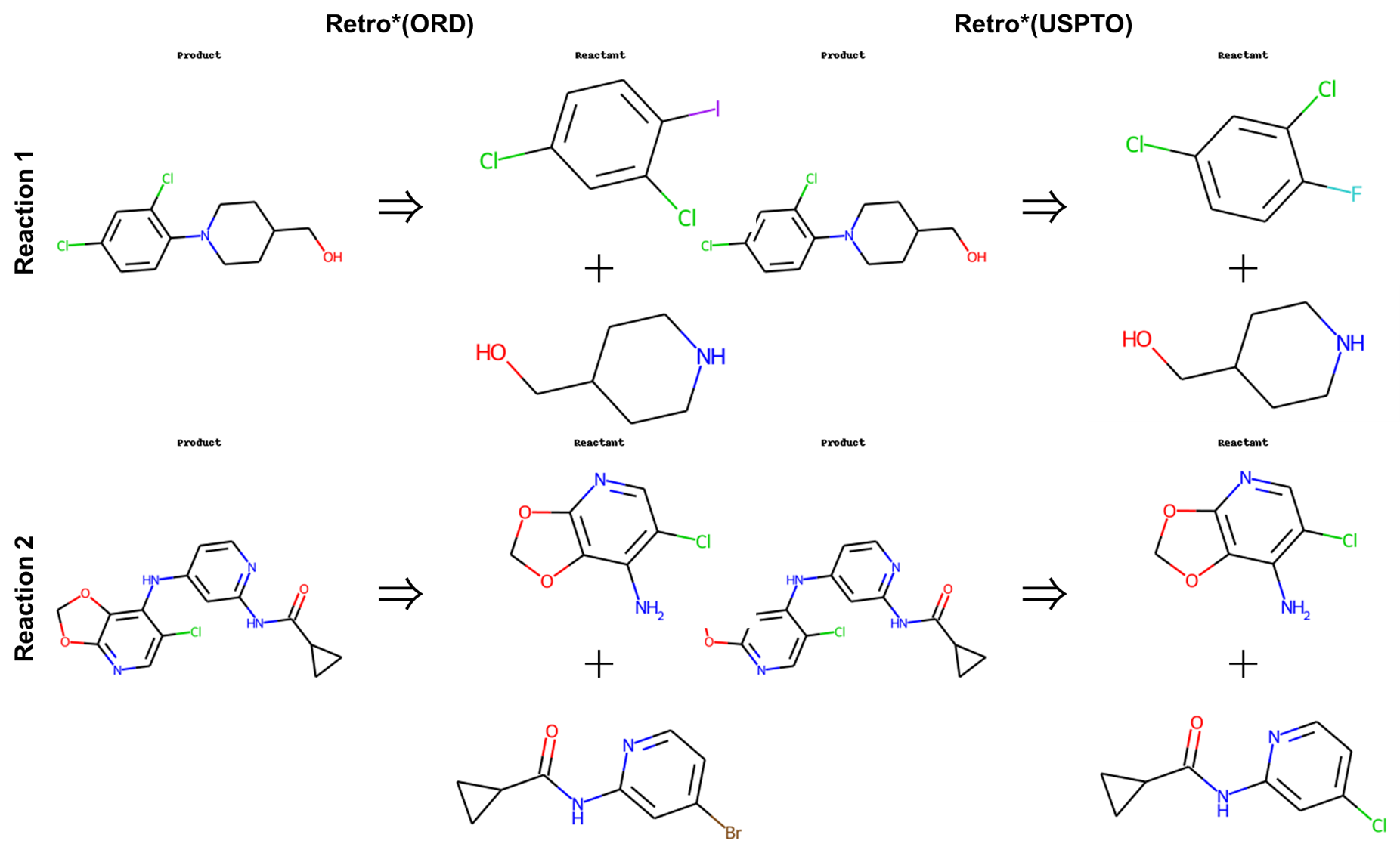
続いて今回使用したORDのデータセットの反応物(Retro*の予測としては出発物質になる。)のSMILESを抽出し、出発物質がまとめられているorigin_dict.csvに追加して、再度逆合成経路の予測を行いました。
その結果、75反応中71反応において逆合成経路を予測することができました。
このことから、origin_dict.csvに記載されている化合物に達するまでに必要な反応が、今回新たに学習させた際に使用したテンプレートデータに含まれていなかったため、逆合成経路予測ができなかったと考えられます。
また、この時、出発物質として選べる分子が増えたため、先ほど複数ステップの逆合成経路が予測されいた反応についても1ステップの逆合成経路予測にとどまっており、その予測された出発物質は、例えば以下のようにORDに記載のものと同一でした。
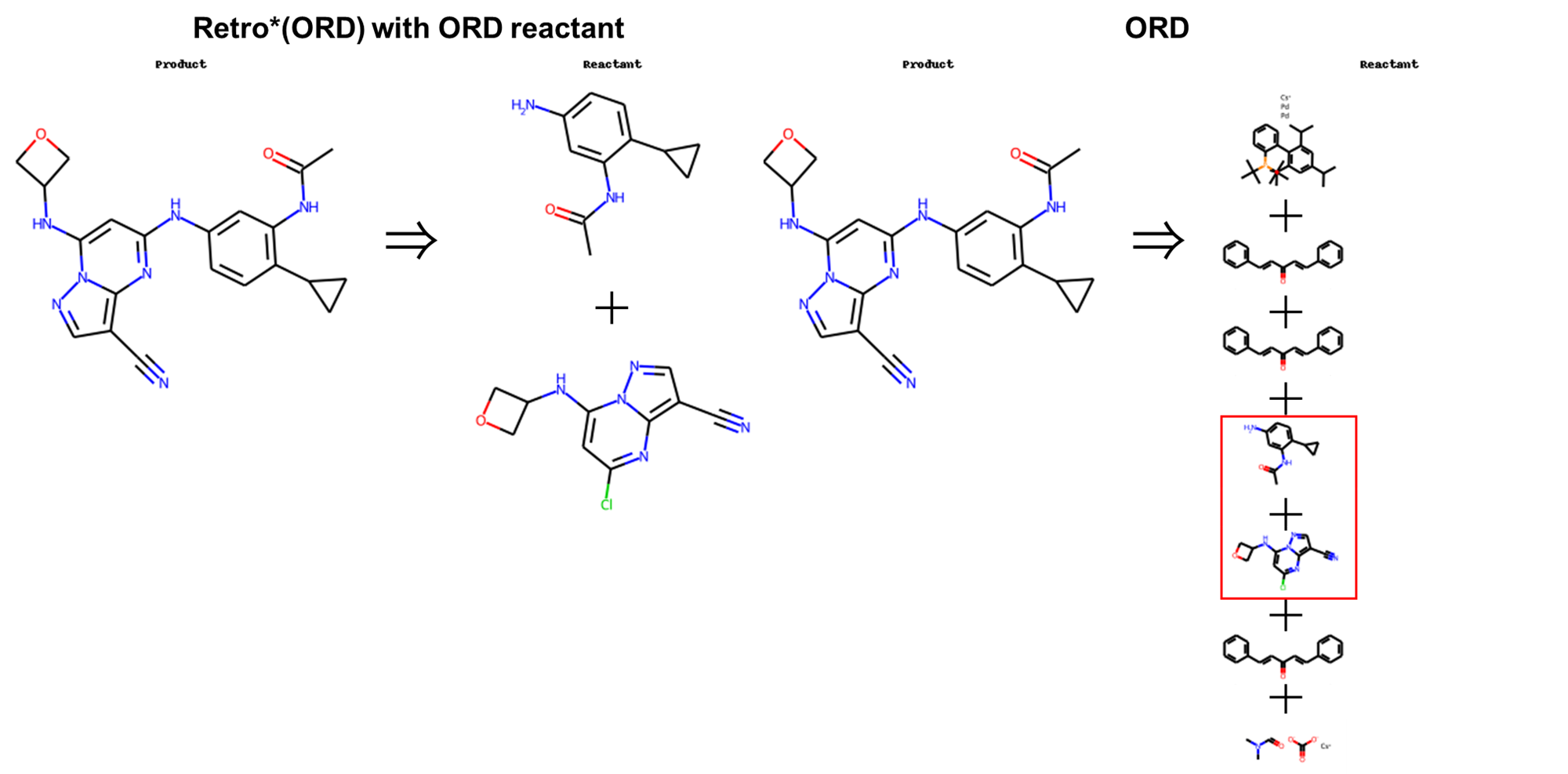
最後に、出発物質がまとめられているorigin_dict.csvにORDのデータセットの反応物(Retro*の予測としては出発物質になる。)のSMILESを追加しても、逆合成経路を予測できなかった4つの反応についてplannerを定義する際に次のようにviz=Trueを指定することで、予測経路を可視化し、その原因を調査しました。
planner = RSPlanner(
gpu=-1,
use_value_fn=True,
mlp_templates=dirpath+'/retro_star/packages/mlp_retrosyn/mlp_retrosyn/data/ord/template_rules_1.dat',
mlp_model_dump=dirpath+'/retro_star/packages/mlp_retrosyn/mlp_retrosyn/data/ord/saved_rollout_state_1_2048_2025-07-14_17:47:53.ckpt',
iterations=100,
expansion_topk=50,
viz=True
)
今回逆合成経路を予測できなかった化合物は次の4つになります。
化合物1: CCOC(=O)C1CC1C(=O)C2=C(C=C(C=N2)N(CC3CC3)C4=CC=C(C5=CC=CC=C54)Cl)OC
化合物2: C1CC2=NN=C(N2C1)C3=CC=C(C=C3)NC4=NC5=C(CN(C[C@H](O5)C6=CC=CC=C6)CCO)C=C4
化合物3: CC1=NN(C=N1)C2=CC=C(C=C2)NC3=NC4=C(CN(C[C@H](O4)C5=CC=CC=C5)C)C=C3
化合物4: CC1=CC(=C(C=C1NC(=O)C)NC2=NC3=C(C=NN3C(=C2)NC4CC4)C#N)F
まず、1つ目の化合物については学習の際に作成したテンプレートに含まれる反応が適応できなかったために、逆合成経路が見つかっていませんでした。予測経路を可視化しか結果は次のようになります。
化合物1
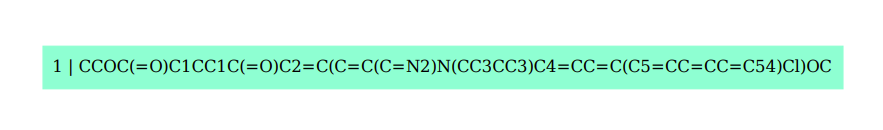
そして残りの3つ反応に関してはテンプレートを適応し逆合成経路は予測できていますが、その結果、ORDに記載されていた化合物と異なる化合物を予測してしまい、そこで得られた化合物から出発物質がまとめられたリストに存在する化合物にたどり着くまでに必要な反応のテンプレートが学習データに存在しなかったため、逆合成経路を見つけることができていませんでした。予測経路を可視化しか結果は次のようになります。
化合物2
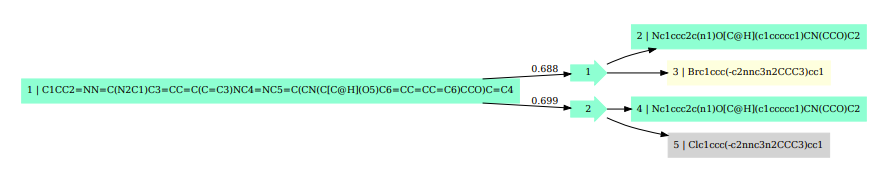
化合物3

化合物4
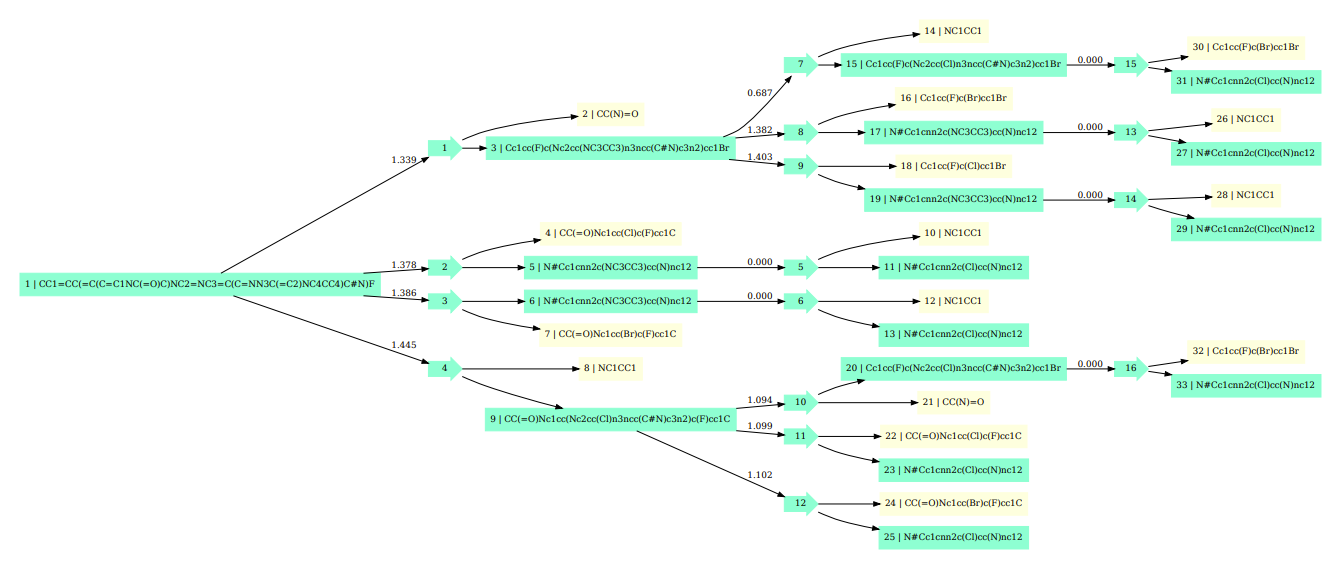
この時SMILESや矢印の色については、灰色がノードがまだ展開されていない状態、緑色は探索が終了した状態、黄色は出発物質がまとめられたリストに存在する化合物であることを示しています。
また、正常に逆合成経路を予測できた反応を可視化すると次のようになり、無事、出発物質がまとめられたリストに存在する化合物までたどり着けた経路については青色で表示されるようになります。
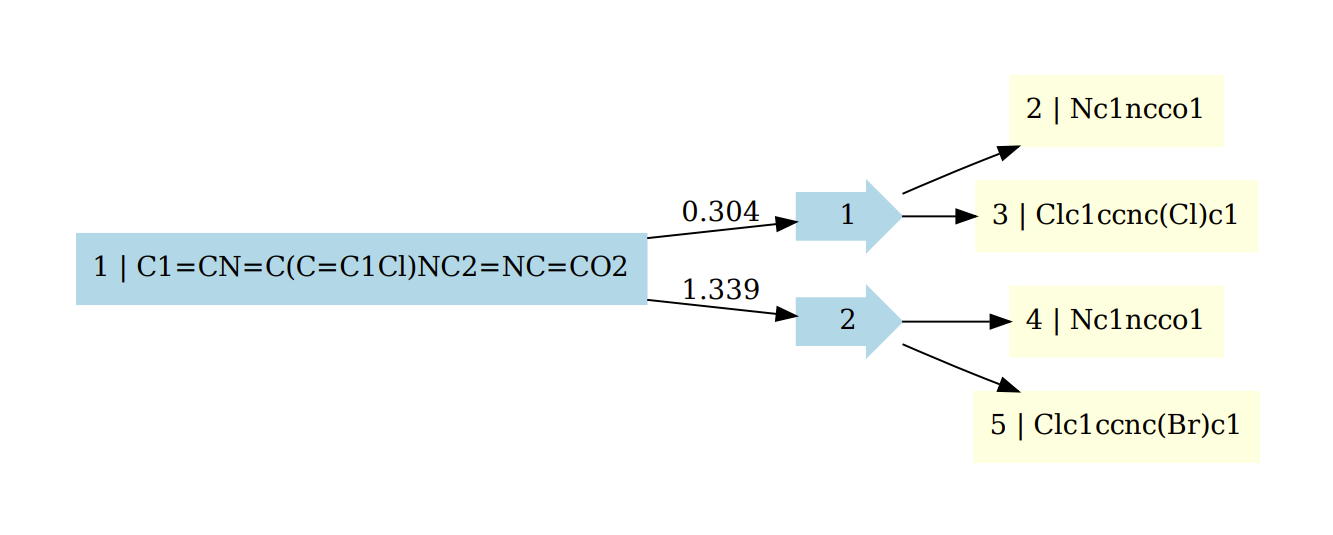
Retro*を学習させる②~Value_MLP
続いて、反応経路途中の化合物のコストを予測するモデルであるValue_MLPの学習を0から行ってみます。Value_MLPは化合物のフィンガープリント(fps)を入力とし、その化合物を合成するのにかかるコストを予測するモデルになります。このモデルの学習には前述したように学習用のTainerクラスが用意されています。また、Retro*のgitにおいても「You can also train your own value function via, python train.py」と記述されており、自分好みのValue関数を作成することができるとわかります。そこで、今回は練習のために先ほど「Retro*を学習させる①」で使用したものと同様の750個の反応からなるORDのデータを利用して、Value_MLPを学習させていきます。
学習に必要なファイルの確認
ValueMLPを学習させるのに必要なファイルをRetro*のgit内で探したのですが、学習に使われている.ptファイル(dataset/train_mol_fp_value_step.pt、dataset/val_mol_fp_value_step.pt)しか見つからず、それをどう作成したのかが不明だったため、今回はその中身の形状やモデル内での使われ方をもとにその中身を推測し、同等のファイルを作成することで、学習に必要なファイルを準備したいと思います。
以下が、dataset/val_mol_fp_value_step.ptの中身になります。
val_mol_fp_value_step.pt
{'n_keys': 6,
'preview': OrderedDict([('fps',
{'byte_size': 32061440,
'dtype': 'uint8',
'nelement': 32061440,
'sample': [0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
'shape': (125240, 256),
'type': 'numpy.ndarray'}),
('values',
{'byte_size': 500960,
'dtype': 'torch.float32',
'nelement': 125240,
'sample': [0.0,
0.0,
0.01931614615023136,
0.0,
0.0,
0.017118854448199272,
0.0,
0.0,
0.0006757445516996086,
0.0],
'shape': (125240, 1),
'type': 'torch.Tensor'}),
('reaction_costs',
{'byte_size': 6618304,
'dtype': 'torch.float32',
'nelement': 1654576,
'sample': [6.907755374908447,
6.907755374908447,
6.907755374908447,
6.907755374908447,
6.907755374908447,
6.907755374908447,
6.907755374908447,
6.907755374908447,
6.907755374908447,
6.907755374908447],
'shape': (1654576, 1),
'type': 'torch.Tensor'}),
('target_values',
{'byte_size': 6618304,
'dtype': 'torch.float32',
'nelement': 1654576,
'sample': [0.01931614615023136,
0.01931614615023136,
0.01931614615023136,
0.01931614615023136,
0.01931614615023136,
0.01931614615023136,
0.01931614615023136,
0.01931614615023136,
0.01931614615023136,
0.01931614615023136],
'shape': (1654576, 1),
'type': 'torch.Tensor'}),
('reactant_fps',
{'byte_size': 1270714368,
'dtype': 'uint8',
'nelement': 1270714368,
'sample': [0, 0, 0, 0, 0, 0, 0, 0, 64, 0],
'shape': (1654576, 3, 256),
'type': 'numpy.ndarray'}),
('reactant_masks',
{'byte_size': 19854912,
'dtype': 'torch.float32',
'nelement': 4963728,
'sample': [1.0, 0.0, 0.0, 1.0, 0.0, 0.0, 1.0, 0.0, 0.0, 1.0],
'shape': (1654576, 3),
'type': 'torch.Tensor'})]),
'type': 'dict'}
上記のように学習に使われているデータはキーとして、fps, values, reaction_costs, target_values, reactant_fps, reactant_masksをもつ辞書形式のデータです。これら6つのデータはそれぞれ
1. fps:2048次元の化合物のフィンガープリントをpackbitsしたデータ
2. values: 予測する値となるその化合物のコスト
3. reaction_costs: 負例となる反応のコスト
4. target_values: 負例と比較するための正例のコスト
5. reactant_fps: 負例反応における反応物のフィンガープリントをpackbitsしたデータ
6. reactant_masks: 有効な負例を判定するマスク行列
であると考えられます。
ここでは、合成にかかるコストにあたる数値を用意できないため、ORDの反応物、生成物、合成収率のデータを利用して、dataset/val_mol_fp_value_step.ptと同様の構造を持つ、合成収率をコストとしたデータセットを作成します。そして、これを用いてValueMLPを学習させることで、合成収率を指標とした逆合成経路予測を行うことを目指します。
学習に必要なファイルの作成
以上の事から、次の6つのデータを持つ辞書型のバイナリファイルの作成を行います。
1. fps:2048次元の化合物のフィンガープリントをpackbitsしたデータ
2. values: 予測する値となるその化合物の合成収率をもとにしたコスト(コストが低いほど収率が良い)
3. reaction_costs: 負例となる反応のコスト(高いコスト)
4. target_values: 負例と比較するための正例のコスト
5. reactant_fps: 負例反応における反応物のフィンガープリントをpackbitsしたデータ
6. reactant_masks: 有効な負例を判定するマスク行列
まず、fpsの作成についてです。fpsに格納される化合物のフィンガープリントは次の関数によって作成します。
morgan_fp_bits
...
def morgan_fp_bits(mol, n_bits, radius):
"""Return uint8 array of shape [n_bits] with {0,1}."""
bv = AllChem.GetMorganFingerprintAsBitVect(mol, radius=radius, nBits=n_bits)
arr = np.zeros((n_bits,), dtype=np.uint8)
DataStructs.ConvertToNumpyArray(bv, arr)
return arr
...
この関数は化合物のMolオブジェクトを受け取り指定した結合距離(radius)及び、ビット数(n_bits)を用いてMorganフィンガープリントを作成し、それをnumpy配列として出力します。今回のケースではradius=2, n_bits=2048を使用しています。
次に、valuesの作成方法は、ORDに記載されている合成収率(yield)の値を用いて、次の関数によって作成します。
yield_to_value
...
def yield_to_value(y_percent, eps):
"""y(%) -> value = -log(max(y/100, eps))."""
y = max(min(float(y_percent) / 100.0, 1.0), eps)
return float(-math.log(y))
...
この関数は百分率で表された合成収率を0から1に規格化し、それを-log(y)の形に変換します。またこの時、最低値としてeps(=0.001)を設定することで、値が無限に発散してしまうことを防ぎます。これにより、0%収率の時値は~6.9078、100%収率の時値は0となり、小さい方が収率の良い値として定義されます。
また、fpsとvaluesの作成時においてあまりにも反応の収率が低い(yield <= zero_threshold=1.0)の反応については、その反応をそのまま負例として扱うこととします。収率の低い反応の反応物をreactant_fpsに加え、負例反応の数を合わせるために、負例反応の数(neg_k)に満たない分はダミー(全て0)のフィンガープリントを追加します。reaction_costsやtarget_valuesには0%収率と同等の-log(eps)=~6.9078を与えます。reactant_masksについては、反応物のフィンガープリントを持つ部分については1をダミーの部分については0を入れています。
low_yield_reaction
...
if y_percent <= zero_thr:
neg_reacts = split_reactants(reac_smi)
neg_smiles_list.append(reac_smi)
rfps, rmask = pack_reactants_fp(
neg_reacts, fp_bits=fp_bits, radius=fp_radius, max_reactants=max_reactants
)
neg_rfps_list.append(rfps)
neg_rmask_list.append(rmask)
neg_rcosts_list.append(margin)
pfp = morgan_fp_bits(pmol, n_bits=fp_bits, radius=fp_radius)
v_fail = float(-math.log(max(min(0.0/100.0, 1.0), eps)))
prod_smiles.append(Chem.MolToSmiles(pmol))
prod_yields.append(y_percent)
product_fps_list.append(pfp)
values_list.append(v_fail)
target_values_rep_list.append(v_fail)
# 2本目以降:ダミーで穴埋め(形状は全ゼロ、maskも0)
for _ in range(neg_k - 1):
neg_smiles_list.append('dummy')
neg_rfps_list.append(np.zeros((max_reactants, fp_bits), dtype=np.uint8))
neg_rmask_list.append(np.zeros((max_reactants,), dtype=np.float32))
neg_rcosts_list.append(margin)
target_values_rep_list.append(v_fail)
# 通常フローはスキップ
continue
...
続いて、reaction_costsの作成についてです。reaction_costsは負例となる反応のコストであるため、0%収率と同等の-log(eps)=~6.9078が与えられます。
そして、target_valuesはその反応におけるvaluesの値が採用されています。
最後に、reactant_fpsとreactant_masksの作成についてです。これらは、次の関数よって作成されます。
make_partial_replace_negative
...
def pack_reactants_fp(reactant_smiles, fp_bits, radius, max_reactants):
"""Return (reactant_fps [max_reactants, fp_bits] uint8, mask [max_reactants] float32)."""
fps = np.zeros((max_reactants, fp_bits), dtype=np.uint8)
mask = np.zeros((max_reactants,), dtype=np.float32)
# 先頭から max_reactants 個だけ使う(超過は切り捨て)
i = 0
for smi in reactant_smiles:
if i >= max_reactants:
break
mol = smiles_to_mol(smi)
if mol is None:
continue # 無効SMILESはスキップ(この位置はゼロベクトルのまま)
fps[i] = morgan_fp_bits(mol, n_bits=fp_bits, radius=radius)
mask[i] = 1.0
i += 1
return fps, mask
def build_negative_pools(df, reactant_col):
"""Group row indices by 'number of reactants' for same-length negative sampling."""
pools: Dict[int, List[int]] = {}
for i, rsmi in enumerate(df[reactant_col].astype(str).tolist()):
n = len(split_reactants(rsmi))
pools.setdefault(n, []).append(i)
return pools
def sample_negative_indices(pools, n_reactants, self_idx, k, rng):
cand = [idx for idx in pools.get(n_reactants, []) if idx != self_idx]
if len(cand) == 0:
return []
if len(cand) >= k:
return rng.sample(cand, k)
# 足りなければ重複許容で補充
return [rng.choice(cand) for _ in range(k)]
def make_partial_replace_negative(df, reactant_col, base_idx, rng,
fp_bits, fp_radius, max_reactants,
pools=None, replace_k=1):
"""正例の反応物を一部入れ替えてネガを作る"""
base_list = [s for s in str(df.iloc[base_idx][reactant_col]).split('.') if s.strip()]
if not base_list:
return None, None
n_r = len(base_list)
rep_cand = []
if pools is not None:
rep_cand = sample_negative_indices(pools, n_r, base_idx, k=replace_k, rng=rng)
if not rep_cand:
# fallback: 全行からランダム
rep_cand = [rng.randrange(0, len(df))]
if rep_cand[0] == base_idx and len(df) > 1:
rep_cand[0] = (rep_cand[0] + 1) % len(df)
neg_list = base_list[:]
for _ in range(replace_k):
j = rng.choice(rep_cand)
alt = [s for s in str(df.iloc[j][reactant_col]).split('.') if s.strip()]
if not alt:
continue
i = rng.randrange(len(neg_list))
neg_list[i] = rng.choice(alt)
rfps, rmask = pack_reactants_fp(neg_list, fp_bits=fp_bits, radius=fp_radius, max_reactants=max_reactants)
return rfps, rmask
...
ここでは、二つの方法によって負例反応の反応物を生成し、それらに基づいてフィンガープリントとマスクを作成します。まず、1つ目の方法では、負例反応として、その生成物をbuild_negative_poolsによってデータセット中のすべての反応物をその数によって分類したpoolsを作成します。そして、これのpoolsの中からsample_negative_indicesによって同じ数の反応物を持つ反応のindexを生成する負例反応の数(k)分生成します。その後、pack_reactants_fpによってmax_reactants個の反応物のSMILESを使ってフィンガープリントを生成します。この時、このネガティブ反応は実在のSMILESを使っているのでマスクの値は1となります。
2つ目の方法では、1つ目と同様にpoolsを作成した後、make_partial_replace_negativeによってフィンガープリントを作成します。ここでは、productを生成する反応の実際の反応物のうち、先頭のSMILESをランダムに抽出した反応の反応物のSMILESに置き換えます。先頭のSMILESを置換する理由は生成物との類似度(タニモト係数)が最も高いため、溶媒や触媒でなく反応の基質である可能性が高いためです。こうしてできた新たな反応物のリストを1つ目と同様にpack_reactants_fpによって処理し、フィンガープリントを作成します。このネガティブ反応も、一部化合物が入れ替わっていますが実在のSMILESを使っているのでマスクの値は1となります。
また、このとき、ネガティブ反応がうまく生成されなかった場合や、生成されたネガティブ反応の数が指定したネガティブ反応の数(k)に満たなかった場合は、以下のようなコードによってダミーのフィンガープリントを作成します。この時、マスクの値は0となります。
dummy_fps
...
rfps = np.zeros((max_reactants, fp_bits), dtype=np.uint8)
rmask = np.zeros((max_reactants,), dtype=np.float32)
...
そして、fpsとreactant_fpsとして作成したフィンガープリントについてはtrain.pyで読み込まれる際にunpackされるようになっているため、以下のようにpack_bitsするようにしています。
pack_bits
...
def pack_bits(arr_float01: np.ndarray) -> np.ndarray:
"""(..., 2048) float{0,1} -> (..., 256) uint8 (packbits)."""
assert arr_float01.shape[-1] == 2048, "last dim must be 2048"
bits = (arr_float01 > 0.5).astype(np.uint8)
return np.packbits(bits, axis=-1)
...
product_fps = np.stack(product_fps_list, axis=0).astype(np.uint8) # [N, 2048]
pack_product_fps = pack_bits(product_fps).astype(np.uint8) # [N, 256]
...
reactant_fps = np.stack(neg_rfps_list, axis=0).astype(np.uint8) # [N*neg_k, max_reactants, 2048]
pack_reactant_fps = pack_bits(reactant_fps).astype(np.uint8) # [N*neg_k, max_reactants, 256]
...
全体のスクリプトは以下のようになります。
build_yield_value_dataset.py
import argparse
import math
import os
import random
from typing import List, Tuple, Dict, Optional
import numpy as np
import pandas as pd
import torch
# RDKit
from rdkit import Chem
from rdkit.Chem import AllChem, DataStructs
# ------------------------------
# Utilities
# ------------------------------
def smiles_to_mol(smiles):
try:
return Chem.MolFromSmiles(smiles)
except Exception:
return None
def canonical_smiles(s):
m = Chem.MolFromSmiles(s)
return Chem.MolToSmiles(m, canonical=True) if m else None
def split_reactants(smiles_concat):
return [s.strip() for s in str(smiles_concat).split('.') if s.strip()]
def pack_bits(arr_float01: np.ndarray) -> np.ndarray:
"""(..., 2048) float{0,1} -> (..., 256) uint8 (packbits)."""
assert arr_float01.shape[-1] == 2048, "last dim must be 2048"
bits = (arr_float01 > 0.5).astype(np.uint8)
return np.packbits(bits, axis=-1)
def morgan_fp_bits(mol, n_bits, radius):
"""Return uint8 array of shape [n_bits] with {0,1}."""
bv = AllChem.GetMorganFingerprintAsBitVect(mol, radius=radius, nBits=n_bits)
arr = np.zeros((n_bits,), dtype=np.uint8)
DataStructs.ConvertToNumpyArray(bv, arr)
return arr
def pack_reactants_fp(reactant_smiles, fp_bits, radius, max_reactants):
"""Return (reactant_fps [max_reactants, fp_bits] uint8, mask [max_reactants] float32)."""
fps = np.zeros((max_reactants, fp_bits), dtype=np.uint8)
mask = np.zeros((max_reactants,), dtype=np.float32)
# 先頭から max_reactants 個だけ使う(超過は切り捨て)
i = 0
for smi in reactant_smiles:
if i >= max_reactants:
break
mol = smiles_to_mol(smi)
if mol is None:
continue # 無効SMILESはスキップ(この位置はゼロベクトルのまま)
fps[i] = morgan_fp_bits(mol, n_bits=fp_bits, radius=radius)
mask[i] = 1.0
i += 1
return fps, mask
def yield_to_value(y_percent, eps):
"""y(%) -> value = -log(max(y/100, eps))."""
y = max(min(float(y_percent) / 100.0, 1.0), eps)
return float(-math.log(y))
def normalize_reactant_set(rsmi):
parts = [p.strip() for p in str(rsmi).split('.') if p.strip()]
can = []
for p in parts:
c = canonical_smiles(p)
if c: can.append(c)
return tuple(sorted(can))
def build_positive_map(df, product_col, reactant_col):
pos = {}
for _, row in df.iterrows():
p = canonical_smiles(str(row[product_col]).strip())
rset = normalize_reactant_set(row[reactant_col])
if p and rset:
pos.setdefault(p, set()).add(rset)
return pos
# ------------------------------
# Negative pools and sampling
# ------------------------------
def build_negative_pools(df, reactant_col):
"""Group row indices by 'number of reactants' for same-length negative sampling."""
pools: Dict[int, List[int]] = {}
for i, rsmi in enumerate(df[reactant_col].astype(str).tolist()):
n = len(split_reactants(rsmi))
pools.setdefault(n, []).append(i)
return pools
def sample_negative_indices(pools, n_reactants, self_idx, k, rng):
cand = [idx for idx in pools.get(n_reactants, []) if idx != self_idx]
if len(cand) == 0:
return []
if len(cand) >= k:
return rng.sample(cand, k)
# 足りなければ重複許容で補充
return [rng.choice(cand) for _ in range(k)]
def make_partial_replace_negative(df, reactant_col, base_idx, rng,
fp_bits, fp_radius, max_reactants,
pools=None):
"""正例の反応物を一部入れ替えてネガを作る"""
base_list = [s for s in str(df.iloc[base_idx][reactant_col]).split('.') if s.strip()]
if not base_list:
return None, None, None
n_r = len(base_list)
rep_cand = []
if pools is not None:
rep_cand = sample_negative_indices(pools, n_r, base_idx, k=1, rng=rng)
if not rep_cand:
# fallback: 全行からランダム
rep_cand = [rng.randrange(0, len(df))]
if rep_cand[0] == base_idx and len(df) > 1:
rep_cand[0] = (rep_cand[0] + 1) % len(df)
neg_list = base_list[:]
j = rng.choice(rep_cand)
alt = [s for s in str(df.iloc[j][reactant_col]).split('.') if s.strip()]
if not alt:
return None, None, None
neg_list[0] = rng.choice(alt)
neg_replace_smi = '.'.join(neg_list)
rfps, rmask = pack_reactants_fp(neg_list, fp_bits=fp_bits, radius=fp_radius, max_reactants=max_reactants)
return rfps, rmask, neg_replace_smi
# ------------------------------
# Main build function
# ------------------------------
def build_dataset(csv_path,product_col,reactant_col,yield_col,fp_bits,fp_radius,max_reactants,neg_k,eps,seed, zero_threshold,neg_partial_ratio=0.5):
rng = random.Random(seed)
zero_thr = float(zero_threshold)
df = pd.read_csv(csv_path)
# 必須列チェック
for col in (product_col, reactant_col, yield_col):
if col not in df.columns:
raise ValueError(f"Column '{col}' not found in CSV.")
# 欠損除去&型
df = df[[reactant_col, product_col, yield_col]].dropna().reset_index(drop=True)
df[yield_col] = df[yield_col].astype(float)
positive_map = build_positive_map(df, product_col, reactant_col)
pools = build_negative_pools(df, reactant_col)
product_fps_list: List[np.ndarray] = []
values_list: List[float] = []
neg_rfps_list: List[np.ndarray] = [] # each: [max_reactants, 2048] uint8
neg_rmask_list: List[np.ndarray] = [] # each: [max_reactants] float32
neg_rcosts_list: List[float] = [] # each: scalar float32
target_values_rep_list: List[float] = []
dropped = 0
margin = float(-math.log(eps)) # 例: eps=1e-3 -> ~6.9078
prod_smiles = []
prod_yields = []
neg_smiles_list = []
def _append_neg(rfps, rmask, smiles_or_none):
# 形状を強制 & None はダミーで埋める
if rfps is None or rmask is None:
rfps = np.zeros((max_reactants, fp_bits), dtype=np.uint8)
rmask = np.zeros((max_reactants,), dtype=np.float32)
smiles = 'dummy'
else:
smiles = smiles_or_none if smiles_or_none is not None else 'dummy'
neg_smiles_list.append(smiles)
neg_rfps_list.append(rfps)
neg_rmask_list.append(rmask)
neg_rcosts_list.append(margin)
target_values_rep_list.append(v)
for idx, row in df.iterrows():
prod_smi = str(row[product_col]).strip()
prod_can = canonical_smiles(prod_smi)
reac_smi = str(row[reactant_col]).strip()
y_percent = float(row[yield_col])
pmol = smiles_to_mol(prod_smi)
if pmol is None:
dropped += 1
continue
n_r = len(split_reactants(reac_smi))
if y_percent <= zero_thr:
neg_reacts = split_reactants(reac_smi)
neg_smiles_list.append(reac_smi)
rfps, rmask = pack_reactants_fp(
neg_reacts, fp_bits=fp_bits, radius=fp_radius, max_reactants=max_reactants
)
neg_rfps_list.append(rfps)
neg_rmask_list.append(rmask)
neg_rcosts_list.append(margin)
pfp = morgan_fp_bits(pmol, n_bits=fp_bits, radius=fp_radius)
v_fail = float(-math.log(max(min(0.0/100.0, 1.0), eps)))
prod_smiles.append(Chem.MolToSmiles(pmol))
prod_yields.append(y_percent)
product_fps_list.append(pfp)
values_list.append(v_fail)
target_values_rep_list.append(v_fail)
# 2本目以降:ダミーで穴埋め(形状は全ゼロ、maskも0)
for _ in range(neg_k - 1):
neg_smiles_list.append('dummy')
neg_rfps_list.append(np.zeros((max_reactants, fp_bits), dtype=np.uint8))
neg_rmask_list.append(np.zeros((max_reactants,), dtype=np.float32))
neg_rcosts_list.append(margin)
target_values_rep_list.append(v_fail)
# 通常フローはスキップ
continue
# 生成物 FP
prod_smiles.append(Chem.MolToSmiles(pmol))
pfp = morgan_fp_bits(pmol, n_bits=fp_bits, radius=fp_radius) # [2048] uint8
product_fps_list.append(pfp)
# 価値ラベル(生成物収率)
prod_yields.append(y_percent)
v = yield_to_value(y_percent, eps=eps)
values_list.append(v)
# ネガティブ生成:同反応物数の他行から neg_k 件
neg_idxs = sample_negative_indices(pools, n_r, idx, neg_k, rng)
added = 0
for j in range(neg_k):
rfps, rmask = None, None
use_partial = (rng.random() < neg_partial_ratio)
if use_partial:
rfps_tmp, rmask_tmp, neg_replace_smi = make_partial_replace_negative(
df, reactant_col, base_idx=idx, rng=rng,
fp_bits=fp_bits, fp_radius=fp_radius, max_reactants=max_reactants,
pools=pools
)
if rfps_tmp is not None:
cand_rset = normalize_reactant_set(neg_replace_smi)
if not (prod_can in positive_map and cand_rset in positive_map[prod_can]):
# 採用
_append_neg(rfps_tmp, rmask_tmp, neg_replace_smi)
added += 1
continue
# ここに来たらフォールバック
use_partial = False
if not use_partial:
if j < len(neg_idxs) and neg_idxs[j] >= 0:
neg_reac_smi = str(df.iloc[neg_idxs[j]][reactant_col]).strip()
cand_rset = normalize_reactant_set(neg_reac_smi)
if prod_can in positive_map and cand_rset in positive_map[prod_can]:
# 衝突: スキップして次へ(added は増やさない)
continue
neg_reacts = split_reactants(neg_reac_smi)
rfps, rmask = pack_reactants_fp(
neg_reacts, fp_bits=fp_bits, radius=fp_radius, max_reactants=max_reactants
)
_append_neg(rfps, rmask, neg_reac_smi)
added += 1
else:
# 候補尽き → ダミー
_append_neg(None, None, None)
added += 1
# 足りない分はダミーで埋める
while added < neg_k:
_append_neg(None, None, None)
added += 1
# まとめて配列化
product_fps = np.stack(product_fps_list, axis=0).astype(np.uint8) # [N, 2048]
pack_product_fps = pack_bits(product_fps).astype(np.uint8) # [N, 256]
values = torch.tensor(values_list, dtype=torch.float32).unsqueeze(1) # [N,1]
pos_df = pd.DataFrame({'SMILES': prod_smiles, 'Value': values_list, 'yield': prod_yields})
# ネガティブは N*neg_k 件の長さ
reactant_fps = np.stack(neg_rfps_list, axis=0).astype(np.uint8) # [N*neg_k, max_reactants, 2048]
pack_reactant_fps = pack_bits(reactant_fps).astype(np.uint8) # [N*neg_k, max_reactants, 256]
reactant_masks = torch.tensor(np.stack(neg_rmask_list, axis=0), dtype=torch.float32) # [N*neg_k, max_reactants]
reaction_costs = torch.tensor(np.array(neg_rcosts_list, dtype=np.float32)).unsqueeze(1) # [N*neg_k,1]
target_values = torch.tensor(np.array(target_values_rep_list, dtype=np.float32)).unsqueeze(1) # [N*neg_k,1]
neg_df = pd.DataFrame({'smiles': neg_smiles_list, 'cost': neg_rcosts_list, 'target_values': target_values_rep_list})
payload = {
"fps": pack_product_fps, # numpy uint8, shape [N, 256]
"values": values, # torch.float32, [N,1]
"reaction_costs": reaction_costs, # torch.float32, [N*neg_k,1]
"target_values": target_values, # torch.float32, [N*neg_k,1]
"reactant_fps": pack_reactant_fps, # numpy uint8, [N*neg_k, max_reactants, 256]
"reactant_masks": reactant_masks, # torch.float32, [N*neg_k, max_reactants]
# 参考情報
"meta": {
"num_rows_in_csv": int(len(df)),
"num_used_products": int(product_fps.shape[0]),
"num_negatives": int(reactant_fps.shape[0]),
"neg_k": int(neg_k),
"fp_bits": int(fp_bits),
"packed_bytes": int(fp_bits // 8 if pack_bits else 0),
"fp_radius": int(fp_radius),
"max_reactants": int(max_reactants),
"eps": float(eps),
"margin": float(margin),
"dropped_rows": int(dropped),
}
}
return payload, pos_df, neg_df
def main():
ap = argparse.ArgumentParser(description="Build yield-based ValueMLP dataset (.pt) from CSV")
ap.add_argument("--csv", required=True, help="Path to CSV with REACTANT, PRODUCT, yield")
ap.add_argument("--output", required=True, help="Output .pt file path")
ap.add_argument("--reactant_col", default="REACTANT")
ap.add_argument("--product_col", default="PRODUCT")
ap.add_argument("--yield_col", default="yield")
ap.add_argument("--fp_radius", type=int, default=2)
ap.add_argument("--max_reactants", type=int, default=3)
ap.add_argument("--neg_k", type=int, default=8)
ap.add_argument("--eps", type=float, default=1e-3)
ap.add_argument("--seed", type=int, default=42)
ap.add_argument("--zero_threshold", type=float, default=0.0,
help="Threshold in PERCENT for zero/failed yields (e.g., 0.0 or 0.5)")
ap.add_argument("--neg_partial_ratio", type=float, default=0.5,
help="部分置換ネガの割合 [0..1]")
args = ap.parse_args()
payload, pos_df, neg_df = build_dataset(
csv_path=args.csv,
product_col=args.product_col,
reactant_col=args.reactant_col,
yield_col=args.yield_col,
fp_bits=2048,
fp_radius=args.fp_radius,
max_reactants=args.max_reactants,
neg_k=args.neg_k,
eps=args.eps,
seed=args.seed,
zero_threshold=args.zero_threshold,
neg_partial_ratio=args.neg_partial_ratio,
)
os.makedirs(os.path.dirname(os.path.abspath(args.output)) or ".", exist_ok=True)
pos_df.to_csv('ord_positive_data.csv', index=False)
neg_df.to_csv('ord_negative_data.csv', index=False)
torch.save(payload, args.output)
meta = payload["meta"]
print(f"Saved: {args.output}")
print(f"- products: {meta['num_used_products']} negatives: {meta['num_negatives']} (neg_k={meta['neg_k']})")
print(f"- dropped rows: {meta['dropped_rows']} margin={meta['margin']:.4f} eps={meta['eps']}")
print(f"- fps dtype={payload['fps'].dtype}, reactant_fps dtype={payload['reactant_fps'].dtype}")
if __name__ == "__main__":
main()
このコードを用いて以下のように自作したORDのデータセットからValueMLPの学習に必要なバイナリファイル(yield_value_train.pt, yield_value_valid.pt)を作成しました。(trainとvalidのデータはあらかじめ9:1の比で分けてあります。)
python build_yield_value_dataset.py \
--csv ./data/ord_valid_data.csv \
--output ./data/yield_value_valid.pt \
--reactant_col REACTANT \
--product_col PRODUCT \
--yield_col yield \
--fp_bits 2048 \
--fp_radius 2 \
--max_reactants 5 \
--neg_k 8 \
--eps 1e-3 \
--seed 42 \
--zero_threshold 1.0 \
--neg_partial_ratio 0.5
今回はnegk=8を指定しているので1反応につき8つの負例反応が追加されます。例えば今回作成したデータの内訳は次のようになりました。
train: products: 675 negatives: 5400
valid: products: 75 negatives: 600
作成したtrainデータの中身は以下のようになっています。
yield_value_train.pt
{'n_keys': 7,
'preview': OrderedDict([('fps',
{'byte_size': 172800,
'dtype': 'uint8',
'nelement': 172800,
'sample': [64, 0, 0, 0, 1, 0, 0, 0, 4, 0],
'shape': (675, 256),
'type': 'numpy.ndarray'}),
('values',
{'byte_size': 2700,
'dtype': 'torch.float32',
'max': 6.907755374908447,
'mean': 2.2183196544647217,
'min': -0.0,
'nelement': 675,
'sample': [0.2427087128162384,
6.907755374908447,
2.3096096515655518,
6.907755374908447,
0.7782694101333618,
1.3257638216018677,
6.907755374908447,
1.715354084968567,
0.6234345436096191,
1.9449106454849243],
'shape': (675, 1),
'type': 'torch.Tensor'}),
('reaction_costs',
{'byte_size': 21600,
'dtype': 'torch.float32',
'max': 6.907755374908447,
'mean': 6.907755374908447,
'min': 6.907755374908447,
'nelement': 5400,
'sample': [6.907755374908447,
6.907755374908447,
6.907755374908447,
6.907755374908447,
6.907755374908447,
6.907755374908447,
6.907755374908447,
6.907755374908447,
6.907755374908447,
6.907755374908447],
'shape': (5400, 1),
'type': 'torch.Tensor'}),
('target_values',
{'byte_size': 21600,
'dtype': 'torch.float32',
'max': 6.907755374908447,
'mean': 2.2183196544647217,
'min': -0.0,
'nelement': 5400,
'sample': [0.2427087128162384,
0.2427087128162384,
0.2427087128162384,
0.2427087128162384,
0.2427087128162384,
0.2427087128162384,
0.2427087128162384,
0.2427087128162384,
6.907755374908447,
6.907755374908447],
'shape': (5400, 1),
'type': 'torch.Tensor'}),
('reactant_fps',
{'byte_size': 6912000,
'dtype': 'uint8',
'nelement': 6912000,
'sample': [0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
'shape': (5400, 5, 256),
'type': 'numpy.ndarray'}),
('reactant_masks',
{'byte_size': 108000,
'dtype': 'torch.float32',
'max': 1.0,
'mean': 0.8105555772781372,
'min': 0.0,
'nelement': 27000,
'sample': [1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0],
'shape': (5400, 5),
'type': 'torch.Tensor'}),
('meta',
{'n_keys': 11,
'preview': OrderedDict([('num_rows_in_csv', {'repr': '675', 'type': 'int'}),
('num_used_products', {'repr': '675', 'type': 'int'}),
('num_negatives', {'repr': '5400', 'type': 'int'}),
('...', '8 more keys')]),
'type': 'dict'})]),
'type': 'dict'}
metaデータが入っているため、keyの数が増えていますが、それを除けば、Retro*で使われていたものと同じ型になっていることがわかります。reactant_fpsやreactant_masksの第2次元が5であるのはmax_reactants=5を指定したためです。(おそらくRetro*ではmax_reactants=3)
ValueMLPの学習
こうして、ValueMLPを学習させるのに必要な学習・検証データが作成できたため、train.pyを用いてValueMLPを学習させます。
!python train.py
学習が完了すると--save_folderで指定した場所に各epochにおけるモデルがepoch_x.ptの形で保存されます。このうち、logを見ながら、最も性能のよかったepochのモデルをbest modelとし、名前を変更しておきます。
これで、ValueMLPの学習は完了です。
学習済みValueMLPの検証
こうして作成したValueMLPの学習済みモデルをRSPlannerのvalue_modelとして指定することで、今回作成したValueモデルを使用したRetro*を実行し、その動きを確かめてみました。
planner = RSPlanner(
gpu=-1,
use_value_fn=True,
value_model='best.pt',
iterations=100,
expansion_topk=50
)
result = planner.plan('CCOC(=O)c1nc(N2CC[C@H](NC(=O)c3nc(C(F)(F)F)c(CC)[nH]3)[C@H](OC)C2)sc1C')
print(result)
print(result == None)
まず、最初に試したのと同様のSMILES(CCOC(=O)c1nc(N2CC[C@H](NC(=O)c3nc(C(F)(F)F)c(CC)[nH]3)[C@H](OC)C2)sc1C)を用いて逆合成予測を行いました。その結果、逆合成経路解析が完了し、次の出力が得られました。
{'succ': True,
'time': 4.551497220993042,
'iter': 7,
'routes': 'CCOC(=O)c1nc(N2CC[C@H](NC(=O)c3nc(C(F)(F)F)c(CC)[nH]3)[C@H](OC)C2)sc1C>0.9844>CCOC(=O)c1nc(N2CC[C@H](N)[C@H](OC)C2)sc1C.CCc1[nH]c(C(=O)O)nc1C(F)(F)F|CCOC(=O)c1nc(N2CC[C@H](N)[C@H](OC)C2)sc1C>0.6764>CCOC(=O)c1nc(N2CC[C@H](NC(=O)OC(C)(C)C)[C@H](OC)C2)sc1C|CCc1[nH]c(C(=O)O)nc1C(F)(F)F>0.9916>[O-][Cl+][O-].CCc1[nH]c(C=O)nc1C(F)(F)F|CCOC(=O)c1nc(N2CC[C@H](NC(=O)OC(C)(C)C)[C@H](OC)C2)sc1C>0.9445>CO[C@@H]1CNCC[C@@H]1NC(=O)OC(C)(C)C.CCOC(=O)c1nc(Br)sc1C|CCc1[nH]c(C=O)nc1C(F)(F)F>0.9994>CCc1[nH]c(C(OC)OC)nc1C(F)(F)F|CCc1[nH]c(C(OC)OC)nc1C(F)(F)F>1.0000>O=C1CCC(=O)N1Cl.CCC1(C(=O)C(F)(F)F)SCCCS1.N.COC(C=O)OC|CCC1(C(=O)C(F)(F)F)SCCCS1>1.0000>CCOC(=O)C(F)(F)F.CCC1SCCCS1',
'route_cost': 0.47280222598984545,
'route_len': 7}
これを構造式に起こすと次のようになります。
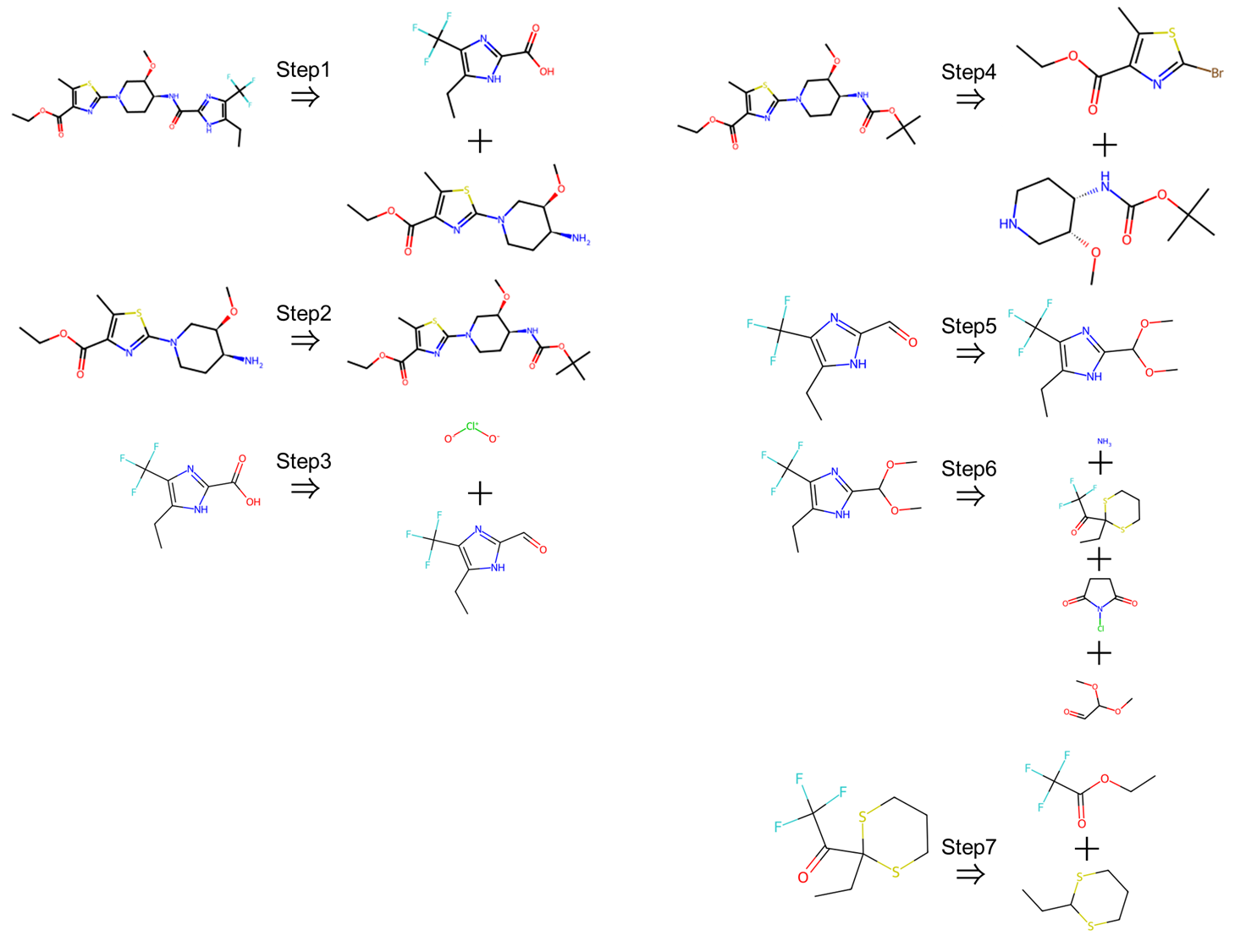
最終的に得られる出発物質は同じですが、Value関数が変わったことにより、それを得るまでの経路が異なり、ステップ数も1つ増えていることがわかります。
ORDで学習したValueMLPの考察
以上のように、新たなデータセットを用いてValueMLPを0から学習し、学習させたモデルをValue関数として用いて逆合成経路を予測させることができました。
ここで、Retro*はValue関数を用いなくても逆反応経路を予測できるため、以下のような設定で同様のSMILES(CCOC(=O)c1nc(N2CC[C@H](NC(=O)c3nc(C(F)(F)F)c(CC)[nH]3)[C@H](OC)C2)sc1C)の予測を行い比較してみました。
planner = RSPlanner(
gpu=-1,
use_value_fn=False,
iterations=100,
expansion_topk=50
)
result = planner.plan('CCOC(=O)c1nc(N2CC[C@H](NC(=O)c3nc(C(F)(F)F)c(CC)[nH]3)[C@H](OC)C2)sc1C')
print(result)
その結果、逆合成経路解析が完了し、次の出力が得られました。
{'succ': True,
'time': 4.511084079742432,
'iter': 7,
'routes': 'CCOC(=O)c1nc(N2CC[C@H](NC(=O)c3nc(C(F)(F)F)c(CC)[nH]3)[C@H](OC)C2)sc1C>0.9844>CCc1[nH]c(C(=O)O)nc1C(F)(F)F.CCOC(=O)c1nc(N2CC[C@H](N)[C@H](OC)C2)sc1C|CCc1[nH]c(C(=O)O)nc1C(F)(F)F>0.9916>CCc1[nH]c(C=O)nc1C(F)(F)F.[O-][Cl+][O-]|CCOC(=O)c1nc(N2CC[C@H](N)[C@H](OC)C2)sc1C>0.6764>CCOC(=O)c1nc(N2CC[C@H](NC(=O)OC(C)(C)C)[C@H](OC)C2)sc1C|CCc1[nH]c(C=O)nc1C(F)(F)F>0.9994>CCc1[nH]c(C(OC)OC)nc1C(F)(F)F|CCOC(=O)c1nc(N2CC[C@H](NC(=O)OC(C)(C)C)[C@H](OC)C2)sc1C>0.9445>CCOC(=O)c1nc(Br)sc1C.CO[C@@H]1CNCC[C@@H]1NC(=O)OC(C)(C)C|CCc1[nH]c(C(OC)OC)nc1C(F)(F)F>1.0000>N.CCC1(C(=O)C(F)(F)F)SCCCS1.O=C1CCC(=O)N1Cl.COC(C=O)OC|CCC1(C(=O)C(F)(F)F)SCCCS1>1.0000>CCOC(=O)C(F)(F)F.CCC1SCCCS1',
'route_cost': 0.47280222598984545,
'route_len': 7}
これを構造式に起こすと次のようになります。
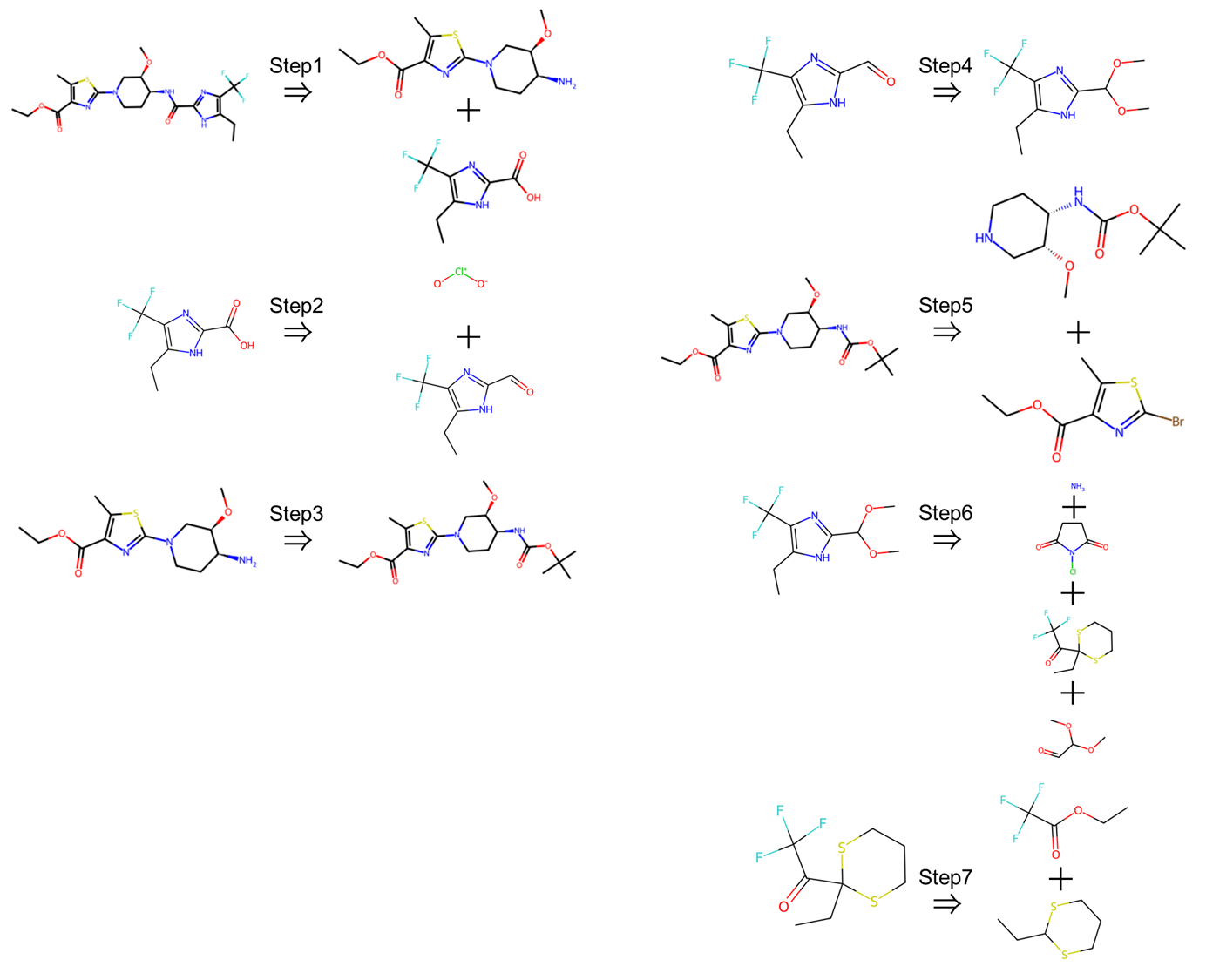
このように、最終的に得られる出発物質は既存のRetro*や今回新たに学習させたValuMLPを用いたRetro*と同じ化合物が得られました。また合成ルートに関しては出力される順番が異なるものの、今回新たに学習させたものと同じルートが出力されました。
今回のValuMLPの学習は小規模なORDのデータセットを使った練習の学習であるため、逆反応予測にはあまり大きな影響を与えることができず、Value関数なしの状態とほぼ同じ結果を与えたのだと考えられます。
ORDを用いて0から学習したRetro*を動かしてみる
最後に今回0から学習しなおしたMLPモデルとValueMLPを組み合わせて、すべてORDを用いて0から学習したモデルを使ったRetro*を動かしてみます。
これまでと同様にORDで学習したMLPモデルとそれに用いたテンプレートはmlp_model_dumpとmlp_templatesで指定し、ValueMLPモデルについてはvalue_modelで指定します。逆合成経路を予測する化合物はMLPモデルの検証の際に用いたこちらのSMILES(CC(=O)NC1=C(C=CC(=C1)NC2=NC3=C(C=NN3C(=C2)NC4COC4)C#N)C5CC5)で表される化合物を使い、以下のコードで実行しました。
planner = RSPlanner(
gpu=-1,
use_value_fn=True,
value_model='best.pt',
mlp_templates=dirpath+'/retro_star/packages/mlp_retrosyn/mlp_retrosyn/data/ord/template_rules_1.dat',
mlp_model_dump=dirpath+'/retro_star/packages/mlp_retrosyn/mlp_retrosyn/data/ord/saved_rollout_state_1_2048_2025-07-14_17:47:53.ckpt',
iterations=100,
expansion_topk=50
)
result = planner.plan('CC(=O)NC1=C(C=CC(=C1)NC2=NC3=C(C=NN3C(=C2)NC4COC4)C#N)C5CC5')
print(result)
その結果、次の逆合成経路が予測されました。
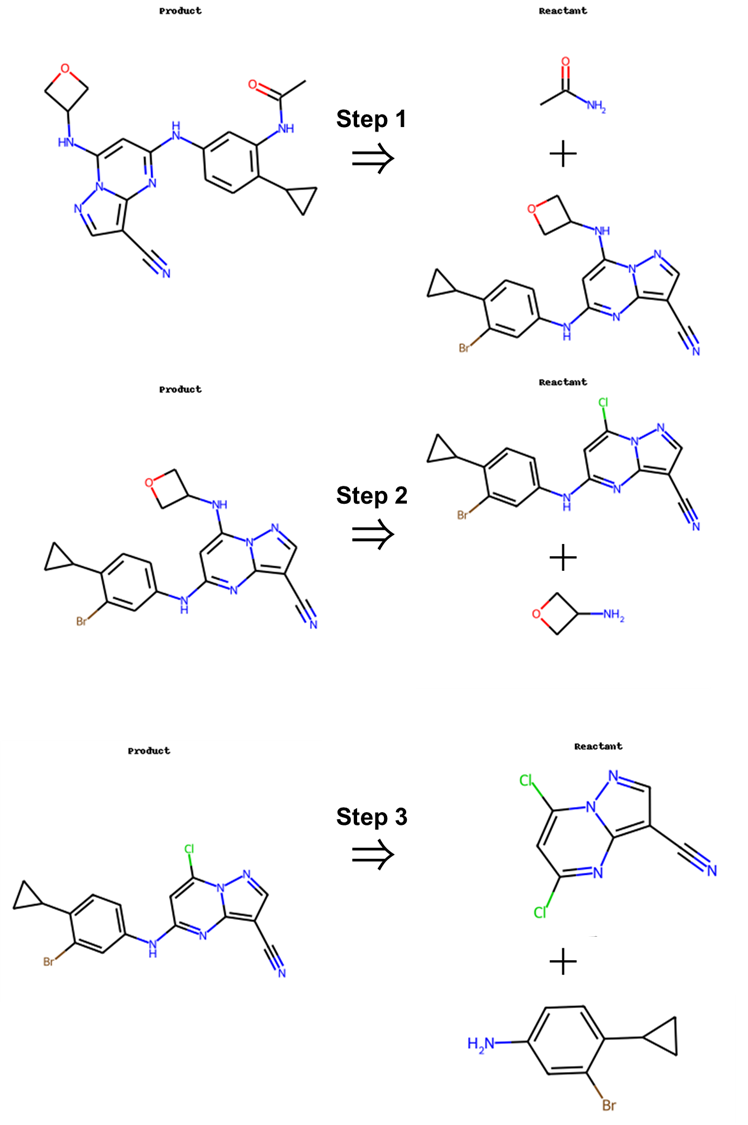
このようにORDで学習したMLPモデルとValueMLPを用いたRetro*(Retro*(ORD+value))では、MLPモデルの検証の際に、ORDで学習したMLPモデルと既存のValueMLPを用いたRetro*(Retro*(ORD))の出力とはやや異なる経路が予測されています。
viz=Trueを指定し、予測経路を可視化してみると、予測されているツリーの構造はほぼ同じですが、Retro*(ORD)では展開され、青色になっていたノードが、未展開のグレーのままになっていることがわかります。
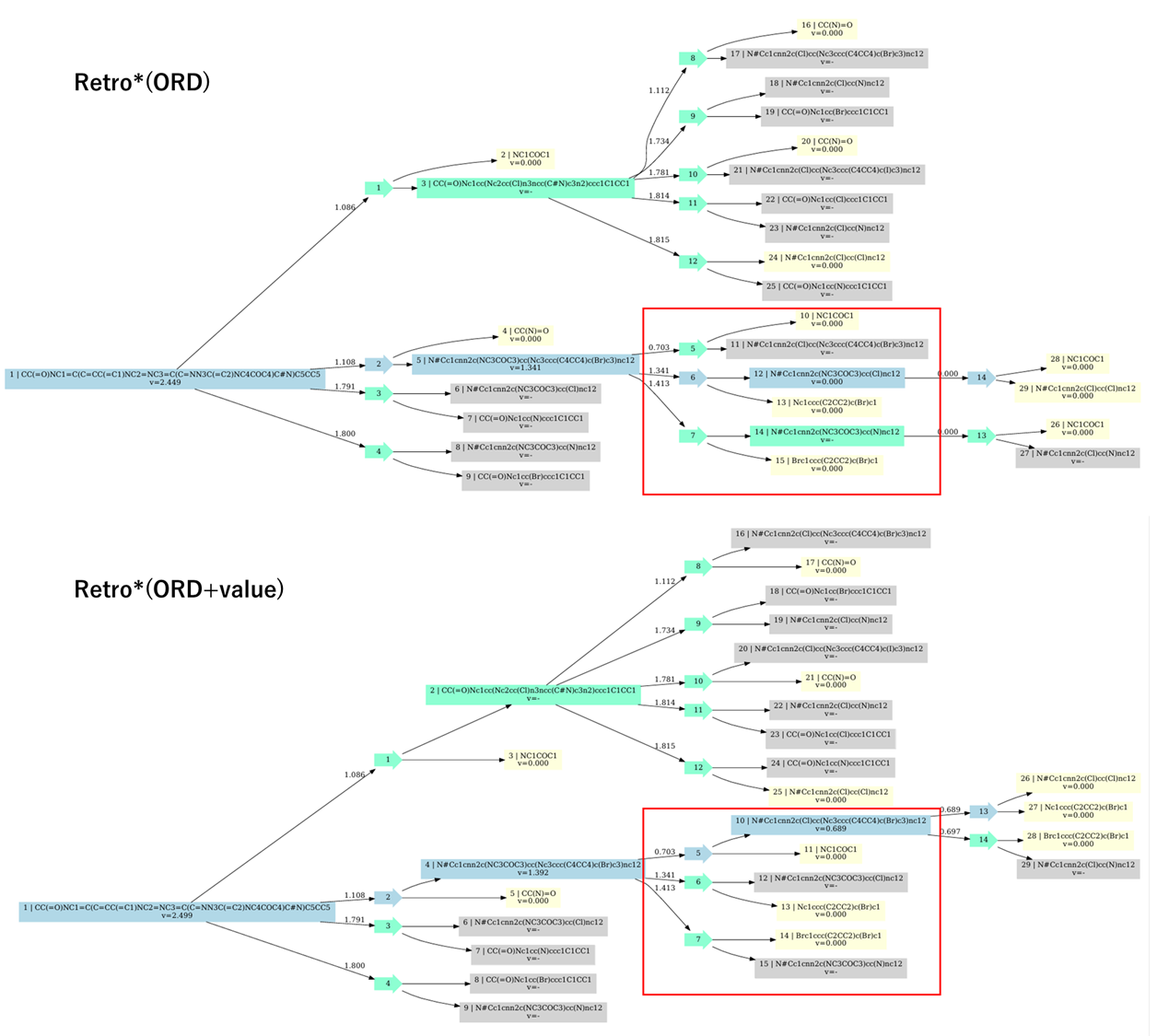
これは、既存のValueMLPと新たに学習したValueMLPとの間で展開するノードの優先度が異なり、これにより予測された逆合成ルートが変わったと考えられます。
まとめ
今回はRetro*を0から動かすことを目標に、Retro*の実装、コード解析・理解、MLPモデルおよびValueMLPの学習を行いました。
現在、逆合成経路予測を行うツールは様々なものがあり、今回紹介したテンプレートベースの探索アルゴリズムを利用したRetro*のほかにも大規模言語モデルを利用したBatGPT-ChemやRetroSynFormerなど様々なものがあります。
近年、主に研究・開発が進められている大規模言語モデルを利用したはRetro*のようにテンプレートを必要としないため、汎用性が高く、未知の反応にも適応しやすいという強みがあります。一方で、これらのモデルはその構造が複雑であったり、学習に膨大なデータが必要であったりとその仕組みを解釈し応用するのは困難です。そこで、今回はモデルの構造が比較的わかりやすく、解釈・応用のしやすいRetro*を用いて、その実装・解析、MLPの学習を通して、その拡張性を検討しました。
この記事の作成にあたり、Value関数については、今回の試行ではあまり大きな変化は見られなかったものの、MLPモデルについては学習に用いるテンプレートを拡張することで、それまでに対応できなかった反応にも適応することがわかりました。また、それに加え、逆合成解析のゴールとなる出発物質の種類を調整することで、それぞれのニーズに合ったRetro*を生成できるのではないかと思います。
(この記事は研究室インターンで取り組みました:https://kojima-r.github.io/kojima/)