はじめに

目的

本ページの目的は不均衡なデータに対処するため Balanced Random Forests の高速なチューニングを試みる。

本ページを読み終えて理解すること

Balanced Random Forests のパラメータチューニングが可能となる。
Balanced Random Forests のパラメータチューニングにより不均衡データに対処可能な機械学習モデルを構築する。
Balanced Random Forests の学術的な背景に触れる。

インストール方法

Balanced Random Forestsのパッケージを利用した日本語のサイトもないようなので下記の方法を掲載(あったら教えてください)。
- pip install -U imbalanced-learn または conda install -c conda-forge imbalanced-learn
- 参考

分析対象データ : 不均衡なクレジット不正利用データ

データ (Kaggle)
- ダウンロード先：Credit Card Fraud Detection
- データの説明
  - 2013年9月にヨーロッパのカード保有者がクレジットカードで行った取引のデータ
  - 284,807 件の取引の内、492件の不正利用が発覚
    - いわゆる不均衡データ
    - 但し書き
      - 本データは一般的なPCでは膨大な計算量がかかり、パラメータチューニングが困難になる。そこで、一部データを抽出してチューニングに焦点を当てる。
  - クレジットカードの利用情報はプライバシーに関わるため、主成分分析により処理された形で特徴量V1からV28がデータに含まれている
    - ただし、時間と合計金額は主成分分析により変換されていない。
  - 分類対象の変数: Class
    - 不正の場合は 1
    - それ以外の場合は 0
- 分析の目的
  - クレジットカードが不正利用されたかどうかを分類可能か？

分析手法

前回は Weight Random Forests (WRF) のパラメーターチューニングを行なった。
- WRFは実はパラメーターチューニングに時間がかかる。前回はおおよそ 16コアマシンで2時間程度だった
今回は Balanced Random Forests (BRF)のパラメーターチューニングを行う。
- WRFと同程度のパラメーターの組み合わせを、16コアマシンで10分程度かかった(20倍程度計算時間が異なる。ただし、クラスラベルの比率に影響するため注意が必要)。

学術的な背景

Chen, Chao, Andy Liaw, and Leo Breiman. “Using random forest to learn imbalanced data.” University of California, Berkeley 110 (2004): 1-12.
- WRF と BRF は Chen et al., 2004にて、不均衡データ分類問題に対処するために提案された。
  - WRFでは不均衡データ分類問題に対処するためコスト重視の学習に焦点をあてた。
    - 構築したモデルを評価する際に、少数派のクラスへの分類を誤ると、重い罰則が科される。
  - BRFでは不均衡データ分類問題に対処するためサンプリング手法に焦点をあてた。
    - 決定木を構築する際に、クラスラベルの比率を考慮してbalanced down-sampled data (例えばクレジットカードの不正利用の数に正常利用の数を合わせる) を利用する。
- これらをPythonで実現するためにはimblearn.ensemble.BalancedRandomForestClassifierが必要

実験

パッケージ読み込み

import numpy as np
import pandas as pd
#from sklearn.model_selection import train_test_split
#from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier
from imblearn.ensemble import BalancedRandomForestClassifier
from sklearn.model_selection import StratifiedKFold, cross_validate
# CatBoostを利用した分類
#from catboost import CatBoostClassifier
#import lightgbm as lgb
#import xgboost as xgb
from sklearn.model_selection import GridSearchCV
# 指標を計算するため
from sklearn.metrics import accuracy_score, cohen_kappa_score, balanced_accuracy_score, make_scorer, f1_score, recall_score
# 見た目を綺麗にするもの
import matplotlib.pyplot as plt
import seaborn as sns
import pprint, pydotplus
from pylab import rcParams
# 保存
from sklearn.externals.joblib import dump
from sklearn.externals.joblib import load

データの読み込み

重要変数
- tata_setは機械学習の用語である特徴量（もしくは特徴変数) を表す
- target_setは機械学習の用語であるクラス (分類対象)を表す

data = pd.read_csv("creditcard.csv")
pd.set_option('display.max_rows', 10)
#print(data.columns) # データの列名確認
# 今回のデータでは、計算量が膨大すぎるのでデータを削減する。現在　284,807 rows × 31 columns
np.random.seed(seed=1)
data = data.sort_values('Class')
# 正常な利用件数を2000件抽出
tmp1 = data.loc[data.loc[:,'Class'] == 0,:].sample(2000) # 
# 不正利用された300権を抽出
tmp2 = data.loc[data.loc[:,'Class'] == 1,:].sample(300)
class_weight_data = {0:1, 1:2300/300}
print(class_weight_data)
data = pd.concat([tmp1,tmp2]) 
#display(data)
target_set = data['Class'] 
data_set = data.loc[:,'V1':'Amount']
#print(target_set,type(target_set)) # クラスラベルの確認
print(data_set,len(data_set.columns)) # 特徴量の確認

BRF グリッドサーチによるチューニング

BRFのパラメータはおおよそ次の通りである。

n_estimators: 木の数 (著者の経験的には 500 から 1000 程度
max_features: 決定木を成長させる際に利用する特徴変数の数 (著者の経験的には sqrt(扱う特徴変数の数)前後
min_samples_leaf:
- リーフ(末端のノード)を構成するのに必要なサンプル数。
min_samples_split: 図解ありの説明な場合はここを参照
- ノードに含まれるサンプルの数が、min_samples_splitに指定された値以上の場合は、決定木の分岐をさらに進める。
max_depth
- 木の大きさを設定する。max_depthの値が大きい場合は過学習を引き起こす傾向がある。
sampling_strategy:imblearn.ensemble.BalancedRandomForestClassifierの翻訳
- 'majority': resample only the majority class; 大多数を占めているクラスのみ再度サンプリング
- 'not minority': resample all classes but the minority class; 少数派のクラス以外の全てのクラスから再度サンプリング
- 'not majority': resample all classes but the majority class; 大多数を占めているクラス以外の全てのクラスから再度サンプリング
- 'all': resample all classes; 全てのクラスから再度サンプリング
- 'auto': equivalent to 'not minority'; 'not minority'を同じ

%%time
model = BalancedRandomForestClassifier(random_state = 43,
                               n_jobs = -1,
                               oob_score=True)
# パラメーターを設定する
param_grid = {"n_estimators": [100,300,500], # 2000まではいらない
              "max_features": [3, 5, 7, None],
#              "class_weight": ['balanced','balanced_subsample',class_weight_data,None],
              "sampling_strategy": ['auto','not majority','majority','all'],
              "min_samples_leaf":  [1, 2, 4],
              "min_samples_split": [2, 5, 10],
              "max_depth": [5,10,None] 
             } 
skf = StratifiedKFold(n_splits=5,
                      shuffle=True,
                      random_state=0)
# パラメータチューニングをグリッドサーチ
grid_result = GridSearchCV(estimator = model,
                           param_grid = param_grid,
                           scoring = make_scorer(cohen_kappa_score), #accuracy, balanced_accuracy
                           cv = skf,
                           return_train_score = True,
                           n_jobs = -1)

grid_result.fit(data_set, target_set)
dump(grid_result,"bmodel_grid_small_data_detil.sav")
reload_best_model = load("bmodel_grid_small_data_detil.sav")

Wall time: 13min 27s

結果のまとめ

先に結果をまとめる

精度
- WRFの精度は 0.916
  - 参考:前回の記事Weight Random Forests (WRF) のパラメーターチューニングを
- BRFの精度は 0.912
パラメータチューニングの時間
- WRFは2.5時間程度
- BRFは0.15時間程度
  - BRFはダウンサイジングされたサンプルを利用するため、高速になる。
  - しかも、それほど精度は変化しないが、1%前後の精度を競うのであればWRFを利用した方が良さそう。
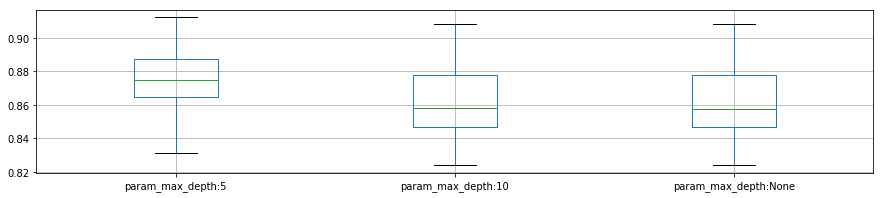
最適なパラメータ
- 'max_depth': 5,
- 'max_features': 3,
- 'min_samples_leaf': 1,
- 'min_samples_split': 2,
- 'n_estimators': 500,
- 'sampling_strategy': 'not majority'
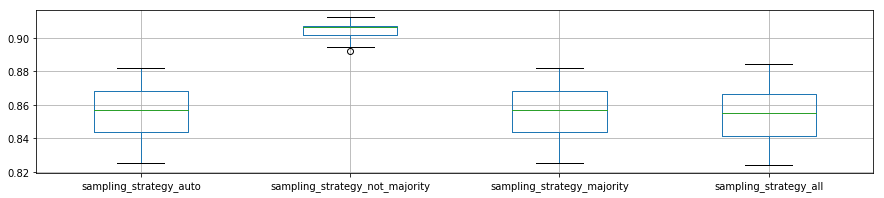
重要なパラメータ
- 'sampling_strategy':
  - 本ページで利用したデータでは'not majority'だけを選べばいいことがわかる。
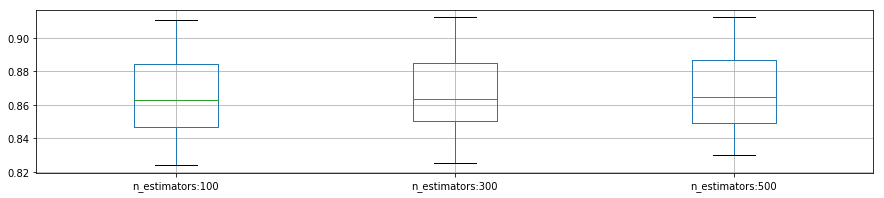
- n_estimators:
  - 決定木を何本作成するかを決めるパラメータのため、増やせば増やすほど計算時間が増加
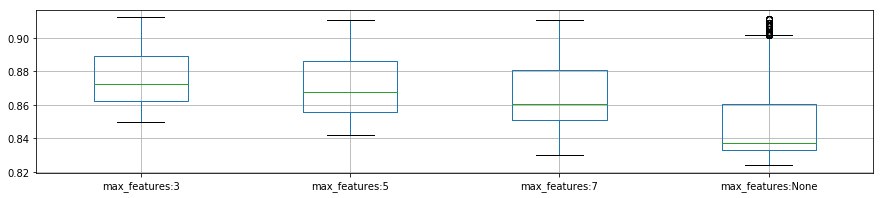
- max_features:
  - 決定木を成長させる際に必要な特徴量の集合の要素数なので、増やせば増やすほど計算時間が増加

#reload_best_model = load("bmodel_grid_small_data_detil.sav")
# ベストな分類器を抽出
pprint.pprint(reload_best_model.best_estimator_)
# ベストなパラメータを抽出
pprint.pprint(reload_best_model.best_params_)
# ベストな正解率を抽出
pprint.pprint(reload_best_model.best_score_)
# 各種途中結果を抽出
pprint.pprint(reload_best_model.cv_results_)

reload_best_model.cv_results_.keys()

dict_keys(['mean_fit_time', 'std_fit_time', 'mean_score_time', 'std_score_time', 'param_max_depth', 'param_max_features', 'param_min_samples_leaf', 'param_min_samples_split', 'param_n_estimators', 'param_sampling_strategy', 'params', 'split0_test_score', 'split1_test_score', 'split2_test_score', 'split3_test_score', 'split4_test_score', 'mean_test_score', 'std_test_score', 'rank_test_score', 'split0_train_score', 'split1_train_score', 'split2_train_score', 'split3_train_score', 'split4_train_score', 'mean_train_score', 'std_train_score'])

各パラメータの変化と精度

plot_p_data = pd.DataFrame( {"n_estimators:100":reload_best_model.cv_results_["mean_test_score"][reload_best_model.cv_results_["param_n_estimators"] == 100],
                             "n_estimators:300": reload_best_model.cv_results_["mean_test_score"][reload_best_model.cv_results_["param_n_estimators"] == 300],
                             "n_estimators:500": reload_best_model.cv_results_["mean_test_score"][reload_best_model.cv_results_["param_n_estimators"] == 500]}
                          )
rcParams['figure.figsize'] = 15, 3
plot_p_data.boxplot()
plt.show()
plot_p_data = pd.DataFrame( {
                             "max_features:3": reload_best_model.cv_results_["mean_test_score"][reload_best_model.cv_results_["param_max_features"] == 3],
                             "max_features:5": reload_best_model.cv_results_["mean_test_score"][reload_best_model.cv_results_["param_max_features"] == 5],
                             "max_features:7": reload_best_model.cv_results_["mean_test_score"][reload_best_model.cv_results_["param_max_features"] == 7],
                             "max_features:None": reload_best_model.cv_results_["mean_test_score"][reload_best_model.cv_results_["param_max_features"] == None]}
                          )
plot_p_data.boxplot()
plt.show()
plot_p_data = pd.DataFrame( {"sampling_strategy_auto":reload_best_model.cv_results_["mean_test_score"][reload_best_model.cv_results_["param_sampling_strategy"] == "auto"],
                             "sampling_strategy_not_majority": reload_best_model.cv_results_["mean_test_score"][reload_best_model.cv_results_["param_sampling_strategy"] == "not majority"],
                             "sampling_strategy_majority": reload_best_model.cv_results_["mean_test_score"][reload_best_model.cv_results_["param_sampling_strategy"] == "majority"],
                             "sampling_strategy_all": reload_best_model.cv_results_["mean_test_score"][reload_best_model.cv_results_["param_sampling_strategy"] == 'all']}
                          )
plot_p_data.boxplot()
plt.show()
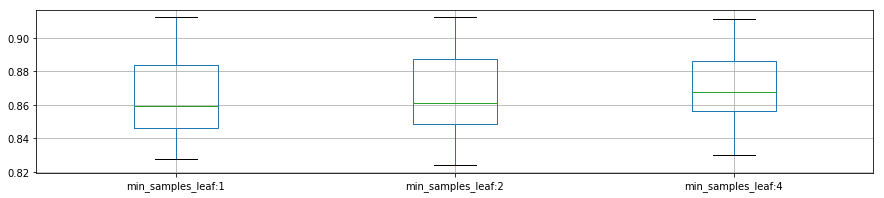
plot_p_data = pd.DataFrame( {"min_samples_leaf:1":reload_best_model.cv_results_["mean_test_score"][reload_best_model.cv_results_["param_min_samples_leaf"] == 1],
                             "min_samples_leaf:2": reload_best_model.cv_results_["mean_test_score"][reload_best_model.cv_results_["param_min_samples_leaf"] == 2],
                             "min_samples_leaf:4": reload_best_model.cv_results_["mean_test_score"][reload_best_model.cv_results_["param_min_samples_leaf"] == 4]}
                          )
plot_p_data.boxplot()
plt.show()
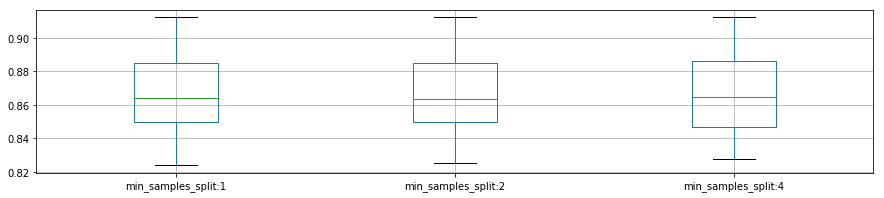
plot_p_data = pd.DataFrame( {"min_samples_split:1":reload_best_model.cv_results_["mean_test_score"][reload_best_model.cv_results_["param_min_samples_split"] == 2],
                             "min_samples_split:2": reload_best_model.cv_results_["mean_test_score"][reload_best_model.cv_results_["param_min_samples_split"] == 5],
                             "min_samples_split:4": reload_best_model.cv_results_["mean_test_score"][reload_best_model.cv_results_["param_min_samples_split"] == 10]}
                          )
plot_p_data.boxplot()
plt.show()
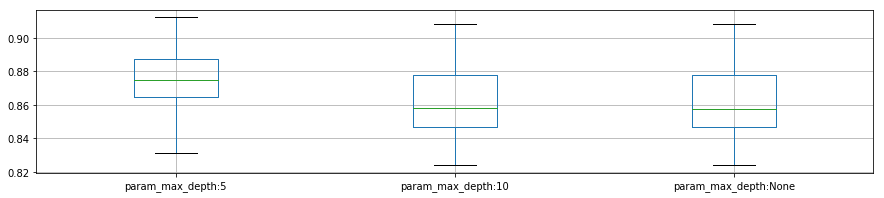
plot_p_data = pd.DataFrame( {"param_max_depth:5": reload_best_model.cv_results_["mean_test_score"][reload_best_model.cv_results_["param_max_depth"] == 5],
                             "param_max_depth:10": reload_best_model.cv_results_["mean_test_score"][reload_best_model.cv_results_["param_max_depth"] == 10],
                            "param_max_depth:None": reload_best_model.cv_results_["mean_test_score"][reload_best_model.cv_results_["param_max_depth"] == None]}
                          )
plot_p_data.boxplot()
plt.show()

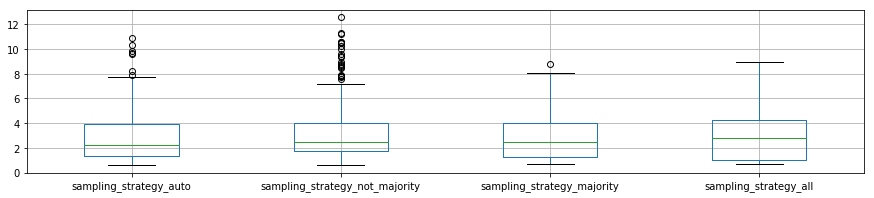
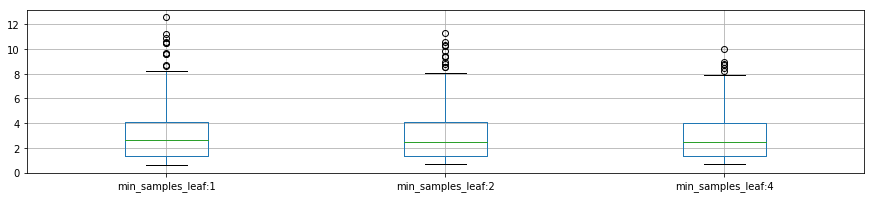
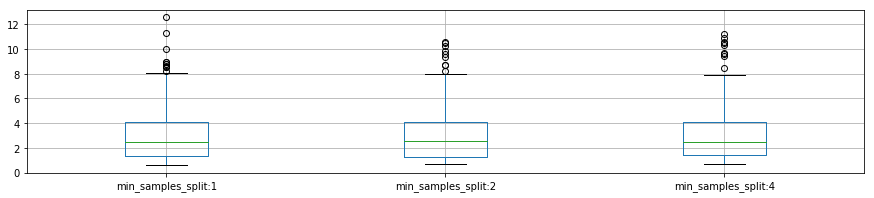
各パラメータの計算時間の分布

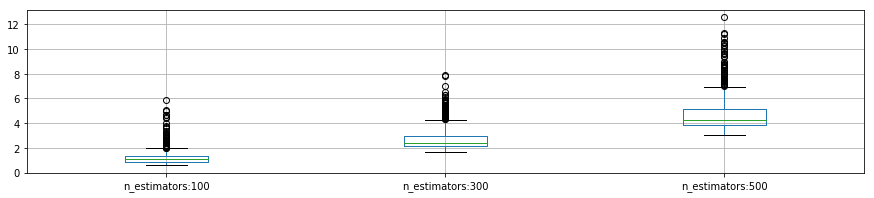
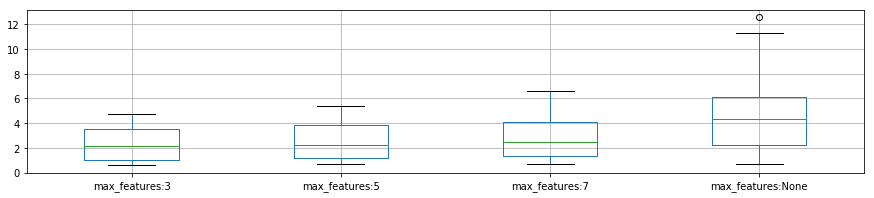
n_estimators と max_features はそれぞれの値が増加すると、計算時間が著しく増える

plot_p_data = pd.DataFrame( {"n_estimators:100":reload_best_model.cv_results_["mean_fit_time"][reload_best_model.cv_results_["param_n_estimators"] == 100],
                             "n_estimators:300": reload_best_model.cv_results_["mean_fit_time"][reload_best_model.cv_results_["param_n_estimators"] == 300],
                             "n_estimators:500": reload_best_model.cv_results_["mean_fit_time"][reload_best_model.cv_results_["param_n_estimators"] == 500]}
                          )
plot_p_data.boxplot()
plt.show()
plot_p_data = pd.DataFrame( {
                             "max_features:3": reload_best_model.cv_results_["mean_fit_time"][reload_best_model.cv_results_["param_max_features"] == 3],
                             "max_features:5": reload_best_model.cv_results_["mean_fit_time"][reload_best_model.cv_results_["param_max_features"] == 5],
                             "max_features:7": reload_best_model.cv_results_["mean_fit_time"][reload_best_model.cv_results_["param_max_features"] == 7],
                             "max_features:None": reload_best_model.cv_results_["mean_fit_time"][reload_best_model.cv_results_["param_max_features"] == None]}
                          )
plot_p_data.boxplot()
plt.show()
plot_p_data = pd.DataFrame( {"sampling_strategy_auto":reload_best_model.cv_results_["mean_fit_time"][reload_best_model.cv_results_["param_sampling_strategy"] == "auto"],
                             "sampling_strategy_not_majority": reload_best_model.cv_results_["mean_fit_time"][reload_best_model.cv_results_["param_sampling_strategy"] == "not majority"],
                             "sampling_strategy_majority": reload_best_model.cv_results_["mean_fit_time"][reload_best_model.cv_results_["param_sampling_strategy"] == "majority"],
                             "sampling_strategy_all": reload_best_model.cv_results_["mean_fit_time"][reload_best_model.cv_results_["param_sampling_strategy"] == 'all']}
                          )
plot_p_data.boxplot()
plt.show()
plot_p_data = pd.DataFrame( {"min_samples_leaf:1":reload_best_model.cv_results_["mean_fit_time"][reload_best_model.cv_results_["param_min_samples_leaf"] == 1],
                             "min_samples_leaf:2": reload_best_model.cv_results_["mean_fit_time"][reload_best_model.cv_results_["param_min_samples_leaf"] == 2],
                             "min_samples_leaf:4": reload_best_model.cv_results_["mean_fit_time"][reload_best_model.cv_results_["param_min_samples_leaf"] == 4]}
                          )
plot_p_data.boxplot()
plt.show()
plot_p_data = pd.DataFrame( {"min_samples_split:1":reload_best_model.cv_results_["mean_fit_time"][reload_best_model.cv_results_["param_min_samples_split"] == 2],
                             "min_samples_split:2": reload_best_model.cv_results_["mean_fit_time"][reload_best_model.cv_results_["param_min_samples_split"] == 5],
                             "min_samples_split:4": reload_best_model.cv_results_["mean_fit_time"][reload_best_model.cv_results_["param_min_samples_split"] == 10]}
                          )
plot_p_data.boxplot()
plt.show()
plot_p_data = pd.DataFrame( {"param_max_depth:5": reload_best_model.cv_results_["mean_test_score"][reload_best_model.cv_results_["param_max_depth"] == 5],
                             "param_max_depth:10": reload_best_model.cv_results_["mean_test_score"][reload_best_model.cv_results_["param_max_depth"] == 10],
                            "param_max_depth:None": reload_best_model.cv_results_["mean_test_score"][reload_best_model.cv_results_["param_max_depth"] == None]}
                          )
plot_p_data.boxplot()
plt.show()

Balanced Random Forestsのパラメーターチューニングを試みる。