hashアルゴリズムとハッシュ値の長さ一覧（＋ハッシュ関数の基本と応用）

Last updated at 2024-12-13Posted at 2018-06-01

「ハッシュ値の衝突」（コリジョン）や「データの改ざん」などの対策で、ベストなハッシュ・アルゴリムを判断するために、ハッシュ値の「長さ」や「速度の目安」一覧が欲しい。

ハ ... ... ハッシュ？
... ってか、ハッシュって、そんなにおいしいの？圧縮された暗号とちゃうん？

TL; DR _{^{_{^{（今北産業）}}}}

この記事はハッシュ関数の出力結果を桁数ごとに、まとめたものです。
- ハッシュ関数の各々の「アルゴリズムが最大何文字・・の 16 進数で返してくるか」の事前確認に利用ください。
マスター、一番強いヤツをくれ。
- バランス優先
  - 👉 sha3-512（64 Byte, 128桁, 2020/12/22 現在）
  - OS やプログラム言語間の互換性・強度・速度の一番バランスが取れているハッシュ・アルゴリズムで強いヤツ。使いやすさなら、SHA3-256。
  - 互換性？
    ここでいう互換性とは「どの言語でも標準・・で大抵は実装しているアルゴリズム」のことです。NIST が制定している Secure Hash Algorithm（略して SHA）のうち、最新版のアルゴリズムであるため、汎用性がとても高いです。最強は SHA3-512 なのですが、現実的で使いやすいのは SHA3-256 でしょうか。
    1 世代前の SHA-2 であっても、SHA256 や SHA512 であれば目くじらたてる必要はありません。しかし、SHA-2 は 20 年前のアルゴリズムであり、クラウドの演算力やブロックチェーンのマイニング・ファームのハッシング演算力が 10 年で激増していることに留意します。というのも 2 世代前の、SHA-1 の効率的な衝突方法の論文が発表されてから Google がそのクラウド演算力を使い実際に衝突例を見つけたこともあり、同系統のアルゴリズムである SHA-2 も両手を広げて安全とは言えなくなったからです。ちなみに、別系統のアルゴリズムである新世代の SHA-3 ですが、NIST が長らく実施していた、量子コンピューター演算にも耐性のある暗号アルゴリズム合戦 "PQC"(Post-Quantum Cryptography) でも、勝者は内部処理の一部でハッシュ関数に SHA3 を使っています。
  - _{^{注意: SHA-3 のライブラリに本家 libXKCP を使っている場合、脆弱性が発見されているので、修正パッチの当たった最新のものを使ってください。OpenSSL 版をベースにしたライブラリなら大丈夫ですが、やはり最新版を使うのをオススメします。}}
    - SHA-3 ライブラリの脆弱性について
      
      2022/10/20 に、SHA-3 のオリジナルを作った Keccak チームが提供している libXKCP ライブラリで、バッファオーバーフローの脆弱性が発見されています。（CVE-2022-37454、CWE-680）
      
      libXKCP の fdc6fef0 のコミットで修正パッチが当たっているので、ライブラリを最新のものにしてください。
      
      PHP
      
      7.4.33 以降で対応
      
      8.0.25 以降で対応
      
      8.1.12 以降で対応
      
      Python (cPython)
      
      3.11 以降で対応（libXKCP の SHA-3 から OpenSSL の SHA-3 に変更）
      
      Debian のパッケージ対応状況
      
      CVE-2022-37454 Tracker | Secrurity Tracker @ debian.org
      
      なお、OpenSSL をベースとしたライブラリには今回の CVE-2022-37454 は問題ありませんが、OpenSSL にもバージョンによって異なる脆弱性があります（CVE-2022-3602、CVE-2022-3786）。
      
      また、この脆弱性を「SHA-3 に脆弱性があった」と記載しているクリックベイトな記事もありますが、実装方法に問題があっただけで、SHA-3 のアルゴリズム自体に脆弱性が見つかったわけではありません。いずれのライブラリを使うにしても最新のライブラリを使うようにしてください。
      
      参考文献
      
      SHA-3 Buffer Overflow @ Nicky Mouha
      
      CVE-2022-37454 @ CVE Report
      
      Buffer overflow in sponge queue functions | Security Advisories | XKCP @ GitHub
      
      #105 Incorrect integer comparisons and buffer overflows | Issue | XKCP @ GitHub
      
      #98517 [CVE-2022-37454] Buffer overflow in the _sha3 module in python versions <= 3.10 | cPython @ GitHub
      
      「XKCP SHA-3」に脆弱性 - 「Python」「PHP」などにも影響 @ Security NEXT
      
      PHPにアップデート、複数脆弱性を修正 @ Secrurity NEXT
- 速度優先
  - 👉 BLAKE3（64 Byte, 128桁, 2021/09/02 現在）
  - OS やプログラム言語間の互換性より「速度優先」の新参ハッシュ・アルゴリズム。
  - 速度優先？
    速度だけを求めると他にもあるのですが、本当に速度だけ・・を求めると沼にハマるので注意しましょう。
    と言うのも、「ハッシュ化しています」と言った途端、常にセキュリティや他の OS・アプリ・プログラム言語とのコラボレーションで比較されるため、選択のバランスが難しいからです。
    例えば、爆速だけどニッチなアルゴリズムを使うと、他のプログラム言語では実装されていなかったりして検証しずらかったりすると、悲しいかな、下手すると「爆速だけど信用できない」といったレッテルを貼られたりします。
    有志による速度や強度の測定に SMhasher などもあり、論文や多言語での実装なども考慮しながら、自分の環境での実測値をベースに総合的に判断する必要があります。
    さて、BLAKE3 は、上記 SHA-3 になり損ねたSHA-3選抜ファイナリストの BLAKE2 の後継です。2021/07/25 に v1.0 をリリースしたばかりの新参であるため、大半の OS やライブラリで査読中などにより標準で実装されていないものが多くあります。そのため、本記事の一覧に含めていません。とは言え、BLAKE2 の知名度・認知度から言っても BLAKE3 はメジャーな（公的機関にも採用されうる）アルゴリズムの 1 つと言っていいでしょう。
    強度は SHA3-256 と同程度とアナウンスされていますが、爆速です。Go 版だと実測で FNV1 より 6 倍以上速かったです ... まじか。
    ちなみに、セキュリティ目的ではない（暗号学的ハッシュを求めない）のであれば、xxHash の xxHash3 (XXH3) が BLAKE3 以上に圧倒的な速度を誇っているので、そこそこ互換性があり CRC より速くて代替となるハッシュを求めている人にはオススメです。[実装言語]
    もし、OS 間やプログラム言語間の互換性をまったく無視するのであれば rapidhash（wyhash の後継）といった C++ に特化したアルゴリズムもあり、沼にハマること受け合いです。
- パスワード目的
  - 👉 Argon2 @ Wikipedia（2015 年 PHC 勝者, 可変長, 2021/03/01 現在）
  - パスワード・ハッシュ^{^[?]}の強度で一番強いアルゴリズム
    _{^{（速いとは言ってない）}}
  - NIST で推奨されている PBKDF2 は強くないの？
    
    NIST の 800-132「パスワードに基づく鍵の導出に関する推奨」で PBKDF2 が推奨されていることからか、パスワードの保存に PBKDF2 を使うケースが見られます。しかし、PBKDF2 は「パスワードの保存」には推奨されていません。
    
    「Password-Based Key Derivation Functions（PBKDF、鍵導出関数）」と「Password Hashing Functions（パスワードハッシュ関数）」は、いくつかの意味合いの違いがあります。
    
    PBKDF は、主にパスワードから安全な鍵（キー）を導出するために使用される関数です。一般的には、鍵派生関数（Key Derivation Function）とも呼ばれます。PBKDF2 はその一例であり、パスワードから派生キーを生成するために使用されます。例えば、パスワードに紐づいたデータの保存や、認証などの紐付け目的で鍵（キー）を派生させるために広く採用されている関数です。しかし、PBKDF は主に鍵を導出することが目的であるため、パスワードを安全に保存するためには追加の手順が必要です。
    
    一方、「パスワードハッシュ関数」は、パスワードをハッシュ値に変換するために使用されます。パスワードハッシュ関数は通常、パスワードの安全な保存に使用され、パスワードの平文を保存することなく、ハッシュ値を比較することで認証を行います。
    
    パスワードハッシュ関数のうち、Argon2id は、PHC 勝者であるパスワードハッシュ関数です。Argon2id は、パスワードをハッシュ化する際にメモリベースの関数として設計され、高いセキュリティレベルと耐性を持っています。
    
    総括すると、PBKDF2 は鍵派生のための関数であり、パスワードの保存には適していません。一方、Argon2id はPHCで優勝した安全なパスワードハッシュ関数であり、パスワードの安全な保存に使用することができます。
TS; DR ではハッシュ関数を完全に理解した気になれる基礎知識と応用例が読めます。
- 読み物です。いささか長いので、ゴロ寝して読んでください。セキュリティ学や暗号学以前の基礎きそ、つまりハッシュ関数の基本中の基本を説明しています。
  読み終わると、ハッシュ使いになった気になり、ブロックチェーン^[?]（台帳式分散データベース）の仕組みの理解、NFT^[?]（分散所有権管理システム）の仕組みが完全に理解できた気になります。さらには IPFS^[?]（分散ファイル・システム）が使える気になります。git（分散バージョン管理システム）が使える人にはおすすめ。

ハッシュ関数とは：ハッシュ関数の基本・特徴
なんで長さなの？：ハッシュ関数の応用
n バイトって HEX 文字列で最大何文字だっけ？：
- 単純に n を２倍してください。
  _{^{１バイト＝0xFF、例：4バイト＝HEXで8桁＝FF FF FF FF}}
なに？4DrlX のような短いハッシュ値を作りたい？：
- ハッシュ値を n 進数に変換して頭の数文字を使うのがいいかも。
この記事は、「❤︎」（旧 LGTM）が付くたびに、何かしら見直したり、手を加えてスパイラル・アップさせています。そのため適宜内容が変わります。変更通知も送りませんので、ストックくださった方はお暇な時に、また覗きに来てください。

ハッシュ・アルゴリズムとビット長の一覧
（ハッシュ値の長さ一覧）

ハッシュ・アルゴリズム一覧

このセクションは WIP です

たくさん「❤︎」を頂いたので "List of hash functions" @ Wikipedia の和訳+自分なりに調べた備考を載せていきたいと思います。が、途中でバテたので「❤︎」がつくたびに少しずつ充実していきたいと思います。

チェックサム系（Check Sum, 誤り検出符号）

アルゴリズム名（関数名含む）	データ長	算出タイプ（系統）	備考
sum8	8 bits	sum	`sum8` は、いわゆる「単純なチェックサム」の代表的なアルゴリズムの 1 つ。検証したいデータを 8 ビットの左シフト、つまり頭から 1 バイト（8 ビット）単位で取り出して得られた数値を加算していき、その合計値に SUM8 のハッシュ値をさらに加算すると、最終合計の末尾 8 ビットが `0` になるアルゴリズム。 SUM8 の値の作り方は、同じように検証データを頭から 8 ビットごとにシフトしながら得た値を加算していき、合計の下位 8 ビットを取り出す。取り出した値をビット反転させてから 1 を加えた値の下位 8 ビット（2 の補数）を SUM8 の値（ハッシュ値）として使う。ハッシュ値と言いながら、ただの足し算である。そのため、速い。ポイントは、SUM 値は合計の下位 8 ビットの補数（それを足すと 1 桁上がる値）になるため、確認側は、すべて加算していき末尾 n 桁が `0` であるか確認するだけなので、実装も楽で処理も速い。_{^{（オンラインで計算を見てみる, Go）}} このように、単純な足し算であるため、データの並び順は関係なくなり（`1+2+3 = 2+1+3`）、0 の並んだデータの違い（`1+0+0+0+1 = 1+1`）も検知できない。つまり `sum` 系は `0` の多いデータや 1 バイト文字の並びに弱いアルゴリズムである。そのため衝突し（異なる引数で同じ値を返し）やすく、意図的な改竄かいざんには極めて弱い。しかし、データ破損の検出率自体は単純計算で 99.6% 以上あり、計算しやすく高速であるため、簡易な誤り検出で速度が必要な場合に使われる。TCP/IP の IP パケットを転送（ルーティング）する際の確認などで使われる。
sum16	16 bits	sum	上記の 16 ビット版
sum24	24 bits	sum	上記の 24 ビット版
sum32	32 bits	sum	上記の 32 ビット版
BSD checksum (Unix)	16 bits	sum	`BSD checksum` は、巡回シフトによる巡回符号のチェックサム・アルゴリズムである。巡回シフトとは、ビット並びを 1 ビットずらし、押し出されたビットを反対側の頭もしくは末尾に持ってくるビット操作である（右巡回のシフト例: `1011` → `1101` → `1110` → `0111` → `1011` → ... 以下同文）。古くから BSD に実装されており sum コマンドなどで使われている。BSD checksum （16 ビット版）の値の作り方は、検証したいデータを上位から 16 ビットずつ読み込み加算していくが、加算する前に合計値を右巡回シフトする。その右巡回シフトした合計値に、読み込み値を加算したら合計値を 16 ビットにトリミングする。つまり、合計値の末尾 16 ビットを抜き出したもの（16 bit なら `1111111111111111` のマスクを AND 演算したもの）を現在の合計値とする。データの読み込みが終わったら、それをチェックサム型のハッシュ値とする。ゆうて、やっていることは、やはり足し算なのである。 `BSD checksum` は `sum32` よりは強いものの、後述する `CRC-32` 型の `cksum` コマンドよりもエラー検知が弱く、`sum32` `CRC` 同様に改竄かいざん耐性はない。つまり、データ（ワード）の順序の変更や、すべてのビットがゼロに設定されたワードの挿入または削除など、一度に多くのビットに影響するいくつかの一般的なエラーを検出できないため「単純なチェックサム」の部類に入る。
SYSV checksum (Unix)	16 bits	sum	巡回シフトによる巡回符号のチェックサム・アルゴリズム。System V の初期から実装されており sum コマンドなどで使われている。CRC-32 型の `cksum` コマンドよりもエラー検知が弱く、CRC 同様に改竄かいざん耐性はない。「単純なチェックサム」の部類に入る。
fletcher-4	4 bits	sum	`Adler-32` の原型ともなったチェックサム・アルゴリズム。単純なチェックサムよりも計算コストは高くなるものの信頼性が高い。`fletcher` の値の具体的な作り方は fletcher-16 で説明するが、n ビットごとに読み込んだ入力データを、2 組の変数に各々異なる組み合わせで加算を行い、定数で剰余演算したものを繰り返し行う。最終的にその 2 組みを上位ビットと下位ビットに割り当てたものがハッシュ値である。また、`fletcher` のハッシュ値を使ったデータの破損の確認は、ハッシュ値からさらに得られる値を、オリジナルのデータに付け加えて同じ `fletcher` の関数に通すと値がゼロになることで、データ破損を検証できる。fletcher-8 や fletcher-16 は TCP のチェックサムのオプションの 1 つにも採用されている¹。Solaris 系のファイルシステムのチェックサムとしても採用されている。使われる定数には、素数の積（合成数）を利用したバリエーションがある。
fletcher-8	8 bits	sum
fletcher-16	16 bits	sum	Go 言語によ実装サンプルを見る
fletcher-32	32 bits	sum
Adler-32	32 bits	sum	zlib の圧縮ライブラリの圧縮や展開／解凍のチェックのために fletcher-16 を改善して開発された。信頼性と引き換えに高速性を追求しているタイプ。同じ長さの CRC よりも速い。信頼性は fletcher-16 と fletcher-32 の中間くらい。IETF の RFC1950 で定義されており、素数の剰余（mod)を利用している。
xor8	8 bits	sum	LRC（Longitudinal Redundancy Check、水平冗長検査）とも呼ばれ、計算方法は ISO 1155 で定義されている。`sum8` に似ているものの、加算時に 8 ビット（`0xFF`）のマスクを合計値にかけることで合計値がオーバーフローしないことと、チェックサムを算出する際の 2 の補数の算出時に `XOR` を使っているのが特徴。具体的には合計にマスク値（`0xFF`）を `XOR` 後 +1 し、下位 8 ビットをチェックサムとする。`XOR8` も `sum8` 同様に 8 ビットごとの加算値に、さらにチェックサム値を加えると末尾 8 ビットが `0` になる。_{^{（オンラインで計算を見てみる, Go）}} ISO 7816 に準拠した IC カードの読み取りや、インターネットの PPP 接続時のシリアル信号（RFC1134）のチェックに使われている。
Luhn algorithm	1 decimal digit	sum
Verhoeff algorithm	1 decimal digit	sum
Damm algorithm	1 decimal digit	Quasigroup operation

CRC 系（Cyclic Redundancy Check, 巡回冗長検査）

アルゴリズム名（関数名含む）	データ長	算出タイプ（系統）	備考
cksum (Unix)	4 Byte (32 bit)	CRC	名残で `checksum` と付いているが、POSIX:2008 (IEEE Std 1003.1-2008) に準拠した CRC-32 アルゴリズムを使ったコマンドであるため CRC に分類される。改竄かいざん耐性はなく、簡単に衝突（ことなる値で同じ出力に）させることができる。
CRC-8	1 Byte (8 bit)	CRC	いわゆる CRC（Cyclic Redundancy Check、巡回冗長検査）系の典型的なアルゴリズムの 1 つ。CRC の `Cyclic`（巡回）は、`CRC-n` の場合、データを上位から n ビットぶんを 1 ビットずつズラしながら参照して演算していくため「巡回」と呼ばれる。前述のチェックサム系アルゴリズムが足し算（加算）をベースにしているのに対し、割り算（除算）をベースにしているアルゴリズムで、余りをハッシュ値とする特殊な剰余算である。 CRC の演算のポイントは 2 つあり、その「割る方の値」（以下「除数」、`divisor`）の算出方法と、実際の CRC の計算方法である。除数の値は定数が使われるが、複数のバリエーション（タイプ）があり、いずれも多項式を用いて算出された定数である。いずれのタイプの除数でも、長さは n ビット + 1 の長さである。（CRC-8 の場合は 9 ビット） CRC の計算方法は「割り算の筆算」（乗除法）に近い方法を使う。つまり、対象の値の左から除数と同じ桁数ぶんを割り、その結果を反映させて 1 桁ずらしてを繰り返す方法に近く、割る代わりに XOR する。具体的には CRC-8 の場合、まずデータの上位 8 ビットを参照し、その値の左端の 1 ビットが 1 の場合は除数と XOR した値と入れ替える。0 の場合は何もしない（次に進む）。次に参照先を右に 1 ビットずらして同様に 8 ビットぶんを参照することを一番右に辿り付くまで繰り返す。つまり、進めるごとに値の左端がどんどん 0 になっていく（具体例）。そして、最終結果の下位 8 ビットが CRC-8 の値として使われる。 CRC 系は隣り合わせのデータを参照していくため、`sum` 系に比べるとデータの並び順に強いものの、離れた位置の違いは検知しにくい（同じ答えになることがある）。そのため、改竄かいざん耐性はないが、バースト（突発的な強いノイズ）などによる一部のビット並びが変わった場合の検知には強いため、シリアル通信のチェックサム値としても使われる。
CRC-16	2 Byte (16 bit)	CRC	CRC の 16 ビット版。シリアル通信系プロトコルのデータチェックによく使われる。除数として使う定数の算出に使われる多項式には、やはりバリエーションがあり、CRC-16 は 22 個が知られている。有名なバリエーションとして、`CRC-16-IBM` の `X¹⁶+X¹⁵+X²+1` は USB や PLCのチェックに使われ、`CRC-16-CCITT` の `X¹⁶+X¹²+X⁵+1` は Bluetooth や SD カードなどのチェックで使われる。_{^{（オンラインでCRC-16-IBMの計算を見てみる, Go）}}
CRC-32	4 Byte (32 bit)	CRC
CRC-32 MPEG-2	4 Byte (32 bit)	CRC
CRC-64	8 Byte (64 bits)	CRC

Adler-32 は CRC であると思われていますが、実質的にはチェックサムの部類に分類されます。

Universal hash function families

アルゴリズム名（関数名含む）	データ長	算出タイプ（系統）
Rabin fingerprint	variable	multiply
tabulation hashing	variable	XOR
universal one-way hash function
Zobrist hashing	variable	XOR

Non-cryptographic hash functions

アルゴリズム名（関数名含む）	データ長	算出タイプ（系統）	備考
Pearson hashing	8 bits (or more)	XOR/table
Paul Hsieh's SuperFastHash[1]	32 bits
Buzhash	variable	XOR/table
Fowler–Noll–Vo hash function (FNV Hash)	32, 64, 128, 256, 512, or 1024 bits	xor/product or product/XOR
Jenkins hash function	32 or 64 bits	XOR/addition
Bernstein's hash djb2	32 or 64 bits	shift/add or mult/add or shift/add/xor or mult/xor
PJW hash / Elf Hash	32 or 64 bits	add,shift,xor
MurmurHash	32, 64, or 128 bits	product/rotation
Fast-Hash	32, 64 bits	xorshift operations
SpookyHash	32, 64, or 128 bits		see Jenkins hash function
CityHash	32, 64, 128, or 256 bits
FarmHash	32, 64 or 128 bits
MetroHash	64 or 128 bits
numeric hash (nhash)	variable	division/modulo
xxHash	32, 64, 128 bits	product/rotation
t1ha (Fast Positive Hash)	64 and 128 bits	product/rotation/XOR/add
pHash	fixed or variable		see Perceptual hashing
dhash	128 bits		see Perceptual hashing
SDBM	32 or 64 bits	mult/add or shift/add	also used in GNU AWK

Keyed Cryptographic Hash Functions

アルゴリズム名（関数名含む）	データ長	算出タイプ（系統）
BLAKE2	arbitrary	keyed hash function (prefix-MAC)
BLAKE3	arbitrary	keyed hash function (supplied IV)
HMAC
KMAC	arbitrary	based on Keccak
MD6	512 bits	Merkle tree NLFSR
One-key MAC (OMAC; CMAC)
PMAC (cryptography)
Poly1305-AES	128 bits	nonce-based
SipHash	32, 64 or 128 bits	non-collision-resistant PRF
HighwayHash	64, 128 or 256 bits	non-collision-resistant PRF
UMAC
VMAC

Unkeyed cryptographic hash functions

アルゴリズム名（関数名含む）	データ長	算出タイプ（系統）
BLAKE-256	256 bits	HAIFA structure[14]
BLAKE-512	512 bits	HAIFA structure[14]
BLAKE2s	up to 256 bits	HAIFA structure[14]
BLAKE2b	up to 512 bits	HAIFA structure[14]
BLAKE2X	arbitrary	HAIFA structure,[14] extensible-output functions (XOFs) design[15]
BLAKE3	arbitrary	Merkle tree
ECOH	224 to 512 bits	hash
FSB	160 to 512 bits	hash
GOST	256 bits	hash
Grøstl	up to 512 bits	hash
HAS-160	160 bits	hash
HAVAL	128 to 256 bits	hash
JH	224 to 512 bits	hash
LSH	256 to 512 bits	wide-pipe Merkle–Damgård construction
MD2	128 bits	hash
MD4	128 bits	hash
MD5	128 bits	Merkle–Damgård construction
MD6	up to 512 bits	Merkle tree NLFSR (it is also a keyed hash function)
RadioGatún	arbitrary	ideal mangling function
RIPEMD	128 bits	hash
RIPEMD-128	128 bits	hash
RIPEMD-160	160 bits	hash
RIPEMD-320	320 bits	hash
SHA-1	160 bits	Merkle–Damgård construction
SHA-224	224 bits	Merkle–Damgård construction
SHA-256	256 bits	Merkle–Damgård construction
SHA-384	384 bits	Merkle–Damgård construction
SHA-512	512 bits	Merkle–Damgård construction
SHA-3 (subset of Keccak)	arbitrary	sponge function
Skein	arbitrary	Unique Block Iteration
Snefru	128 or 256 bits	hash
Spectral Hash	512 bits	wide-pipe Merkle–Damgård construction
Streebog	256 or 512 bits	Merkle–Damgård construction
SWIFFT	512 bits	hash
Tiger	192 bits	Merkle–Damgård construction
Whirlpool	512 bits	hash

ハッシュ値の長さ一覧と速度の目安

すべて同じメッセージをハッシュ化したもの（「Hello Qiita!」のハッシュ値）なのに、ハッシュ値の長さ、つまりビット長が同じでも値がまったく異なることに注目ください。

^{_{🐒 各アルゴリズムの PHP 7.2.6 での計算速度も記載していますが、環境だけでなく PHP のバージョンによってかなり速度が異なります。速度は目安程度にご利用ください。まずは強いアルゴリズムで組んでから、「推測するな、測定せよ」の精神でご自分の環境に最適化することをお勧めします。
なお、SHA-3 に含まれる SHAKE256 などの可変長のアルゴリズム、および SHA-3 の最終選考まで残った BLAKE2 や、その後続で爆速と噂の BLAKE3 は、まだライブラリが枯れて（OS やプログラム言語で浸透）していないため含めていません。}}

仕様

検証環境：macOS HighSierra（OSX 10.13.6）, PHP 7.2.6（cli）, MacBookPro Early 2015, 2.7GHz Corei5, Mem 8GB 1867MHz DDR3
ハッシュするメッセージ：「Hello Qiita!」
ループ回数：1,000,000 回（100 万回）
速度：上記ループの 10 回ぶんの平均値
並び順：桁数の少ない順 → 速い順
メッセージダイジェストは横スクロールをさけるため 8 桁（4バイト）ごとのブロックに分けています。
測定のソースコード @ Paiza.IO

8 桁のハッシュ値

アルゴリズム	バイト長	速度	ハッシュ値
`fnv132`	`4 Byte`	`0.157887 sec`	`b04649f6`
`fnv1a32`	`4 Byte`	`0.157962 sec`	`129b42dc`
`adler32`	`4 Byte`	`0.165301 sec`	`1bf5042e`
`crc32`	`4 Byte`	`0.169681 sec`	`dd54ff69`
`crc32b` `(IEEE)`	`4 Byte`	`0.172050 sec`	`ad6adc0d`
`joaat`	`4 Byte`	`0.173369 sec`	`2cbbf315`

16 桁のハッシュ値

アルゴリズム	バイト長	速度	ハッシュ値
`fnv164`	`8 Byte`	`0.168120 sec`	`97bfaffd` `885daad6`
`fnv1a64`	`8 Byte`	`0.176964 sec`	`07c72cc2` `7b5f8b5c`

32 桁のハッシュ値

アルゴリズム	バイト長	速度	ハッシュ値
`md4`	`16 Byte`	`0.284748 sec`	`e2500f3f` `1eb028a4` `563ca3d4` `35028996`
`md5`	`16 Byte`	`0.337097 sec`	`7c414ef7` `535afff2` `1e05a36b` `1cfc9000`
`tiger128,3`	`16 Byte`	`0.341727 sec`	`60bd4df9` `e039716f` `07c9ecd4` `4c203d34`
`tiger128,4`	`16 Byte`	`0.397596 sec`	`7c20d9b5` `d9e79da7` `b5241a08` `a353018a`
`ripemd128`	`16 Byte`	`0.553369 sec`	`0ff7eaf1` `38540680` `8e92e642` `28a79243`
`haval128,3`	`16 Byte`	`0.954699 sec`	`a8fe5c62` `4c856077` `d07db6bc` `9a7f1275`
`haval128,4`	`16 Byte`	`1.027350 sec`	`b5ee64c0` `6a003d55` `65108356` `08c6a34c`
`haval128,5`	`16 Byte`	`1.197690 sec`	`ad189ff3` `183c9cfe` `cf5a39e3` `45ba95f8`
`md2`	`16 Byte`	`4.762099 sec`	`8cd3c9c1` `f1079b15` `639ddab1` `2227d400`

40 桁のハッシュ値

アルゴリズム	バイト長	速度	ハッシュ値
`sha1`	`20 Byte`	`0.348829 sec`	`5d8793ae` `d96d808a` `b6af8e47` `5ce244e8` `a604e478`
`tiger160,3`	`20 Byte`	`0.367638 sec`	`60bd4df9` `e039716f` `07c9ecd4` `4c203d34` `6f07e46a`
`tiger160,4`	`20 Byte`	`0.399170 sec`	`7c20d9b5` `d9e79da7` `b5241a08` `a353018a` `bf178a02`
`ripemd160`	`20 Byte`	`0.694799 sec`	`99a6c172` `52ae4e64` `e8d22853` `c54ee2ad` `44089160`
`haval160,3`	`20 Byte`	`0.900242 sec`	`aba140dc` `e20ac7a2` `615053de` `4336e343` `37a49b46`
`haval160,4`	`20 Byte`	`1.033398 sec`	`6bc4fecd` `c33d5d21` `14c695ff` `f449d333` `58f3030d`
`haval160,5`	`20 Byte`	`1.197252 sec`	`d87a41cb` `73469426` `42faf2ae` `7d62e81a` `eba5dcc6`

48 桁のハッシュ値

アルゴリズム	バイト長	速度	ハッシュ値
`tiger192,3`	`24 Byte`	`0.394713 sec`	`60bd4df9` `e039716f` `07c9ecd4` `4c203d34` `6f07e46a` `9c308ef7`
`tiger192,4`	`24 Byte`	`0.410200 sec`	`7c20d9b5` `d9e79da7` `b5241a08` `a353018a` `bf178a02` `0a74f3fb`
`haval192,3`	`24 Byte`	`0.874294 sec`	`e2b0c018` `6b1cc119` `0eebe1be` `9d61953d` `2dd78ba4` `8136086c`
`haval192,4`	`24 Byte`	`1.031765 sec`	`7540fa22` `a5714124` `cf942e1b` `31a890b9` `bb59d58c` `e5a61157`
`haval192,5`	`24 Byte`	`1.211350 sec`	`e4a6b10a` `d8286eaf` `8cb3f225` `950c2f93` `b6fdab8c` `601626c8`

56 桁のハッシュ値

アルゴリズム	バイト長	速度	ハッシュ値
`sha224`	`28 Byte`	`0.713225 sec`	`d72d6ef7` `0a788b3e` `7f720b5d` `88f20a13` `bf161c31` `b260fd34` `6573094d`
`sha3-224`	`28 Byte`	`0.817025 sec`	`e833eab3` `4fbefbe8` `9e44dcf1` `d4ea9990` `10981761` `22f51708` `df9cd9d0`
`sha512/224`	`28 Byte`	`0.825188 sec`	`e205b15d` `16eda0ce` `e195d210` `73edca14` `a69198e9` `0070b9b0` `09f7cb16`
`haval224,3`	`28 Byte`	`0.842655 sec`	`a69049ca` `88565098` `a6f5e2bc` `adb22980` `e59da983` `9a779b63` `c214e019`
`haval224,4`	`28 Byte`	`1.045480 sec`	`090b25d0` `e8a0f5ef` `ecf6b683` `5be72fe5` `6913b34e` `2d086922` `3b1ac5d1`
`haval224,5`	`28 Byte`	`1.209415 sec`	`5343b4b1` `a16119c5` `dcd7726e` `53128841` `fecb7607` `88e9008f` `6c6f2cb6`

64 桁のハッシュ値

アルゴリズム	バイト長	速度	ハッシュ値
`ripemd256`	`32 Byte`	`0.574046 sec`	`e0fe9c49` `b1a59fae` `47096909` `83e62829` `4887b161` `5722a62c` `2c4187be` `816b058d`
`sha256`	`32 Byte`	`0.668654 sec`	`e863d36c` `24ada694` `fa77454b` `33e8f9b9` `545d372a` `ae251e87` `79fc25df` `16943fed`
`sha3-256`	`32 Byte`	`0.824698 sec`	`cedaea23` `33478d77` `bc9ed3e3` `3303f455` `85af1917` `4a451ce9` `3029fedc` `dd4d1ecb`
`sha512/256`	`32 Byte`	`0.833001 sec`	`aaa2e875` `112de9b6` `1744d4a0` `ae757e40` `cd12008a` `0f3948fb` `7c42a8cd` `48c361b8`
`haval256,3`	`32 Byte`	`0.845439 sec`	`5f788c8a` `5359387b` `acf7bf60` `ff4dd08d` `e7176205` `a0aae1ce` `4f485b40` `126c0d2f`
`haval256,4`	`32 Byte`	`1.048196 sec`	`4ebb9e6f` `a6c045b0` `cbba419e` `f06ac973` `b2fd4914` `f746e142` `bb6b840f` `bd836158`
`haval256,5`	`32 Byte`	`1.218753 sec`	`c99614ae` `a2985f43` `f480d029` `bcb7974b` `f5aface5` `8730c9d6` `f3141a67` `58270431`
`gost`	`32 Byte`	`1.828385 sec`	`667f4328` `0ff9e0a5` `9c15de57` `022becf3` `cd1a48f8` `d37a165c` `87576b6f` `814fa482`
`gost-crypto`	`32 Byte`	`1.849877 sec`	`7ebf0f97` `0f1246b6` `aea110d7` `32cbcdfd` `b0169cf1` `7336bae7` `814e99f1` `8abfbd21`
`snefru`	`32 Byte`	`2.841073 sec`	`ad081810` `0ab15234` `b13b8d09` `ad0c519a` `35469221` `adbf8c5f` `a71594ca` `f7dfddc2`
`snefru256`	`32 Byte`	`2.850217 sec`	`ad081810` `0ab15234` `b13b8d09` `ad0c519a` `35469221` `adbf8c5f` `a71594ca` `f7dfddc2`

80 桁のハッシュ値

アルゴリズム	バイト長	速度	ハッシュ値
`ripemd320`	`40 Byte`	`0.725499 sec`	`6d152e32` `fee2b979` `024b8cff` `e416c898` `16032680` `779f7c3a` `93c9aa26` `35441245` `8d4a9010` `ad8fdfa5`

96 桁のハッシュ値

アルゴリズム	バイト長	速度	ハッシュ値
`sha384`	`48 Byte`	`0.831855 sec`	`b10497cf` `49601678` `4d8413a4` `662983a8` `dc4ac470` `039ea755` `d5ec985f` `1aab04ee` `26dc3d67` `71bbe404` `75ea7d13` `5a97ba58`
`sha3-384`	`48 Byte`	`0.835068 sec`	`e83e54ee` `323dafb5` `ca2d800f` `d479e1cc` `94502362` `93d5ad74` `36228519` `aa657ea3` `d1da8bb6` `2d07035d` `ec1ece2f` `428ec8dc`

128 桁のハッシュ値

アルゴリズム	バイト長	速度	ハッシュ値
`sha3-512`	`64 Byte`	`0.851400 sec`	`9d1aaed0` `79bac194` `6a5fbafb` `4285ec5b` `dcf0053a` `9e005590` `46884a14` `8f28fcb9` `02441b49` `cb3a8277` `5834a244` `4dd183ed` `a36cee90` `0f5662f8` `2353fae7` `e7111740`
`sha512`	`64 Byte`	`0.860255 sec`	`cac9036c` `1dd3652f` `c550e99a` `4ec2b066` `d69d6a40` `a369bc85` `e3078960` `e6f26012` `4138f5d0` `f4e9a6e0` `47dfb833` `c9dd9b33` `76d02d49` `be37de26` `dd6234d4` `e79cc09e`
`whirlpool`	`64 Byte`	`1.041927 sec`	`488c6cd6` `eccb5348` `8a7c7617` `8c89d514` `16b8eb2b` `88a30b79` `71f1f176` `70e27659` `fc477cd9` `6ade86e4` `b6176c5e` `f2f67068` `89606786` `4ce15443` `eff90733` `fd4fcf4c`

TS; DR _{^{最速のDBキー検索を求めて with SQLite3}}

ハッシュ値の衝突は別のアルゴリズムでは衝突しない _{^{_{^{（限りなく）}}}}

衝突のイメージ

// 値が微妙に異なる $a と $b
$a = 'xxxxxxxxx..1..xxxxxxxxx'; // 長ったらしい文字列 a
$b = 'xxxxxxxxx..0..xxxxxxxxx'; // 長ったらしい文字列 b

$result_sha1 = ( hash('sha1', $a) === hash('sha1', $b) );
$result_md5  = ( hash('md5',  $a) === hash('md5',  $b) );

// $result_sha1 --> true, 偶然にも衝突が発生！
// $result_md5  --> false, アルゴリズムが異なると衝突しない（可能性が高い）

古くはダウンロード・ページなどでファイルの改ざんや破損がないかを比べるのに使われていたり、身近なところではアクセス・トークンの作成、いつもお世話になっているパッケージマネージャーのパッケージ管理、データベース（以下 DB）のクラスタリングや負荷分散、みんな大好き Git のコミットID にも使われている「ハッシュ関数」。

Linux のニッチで老舗のパッケージマネージャーである Nix では、ハッシュ値を全面的に使うことで依存関係を徹底的に管理しています。最近、頭角を現している Linux の異端児 NixOS は、その仕組みを OS レベルで使う（カーネル含む全てのシステム・ファイルをハッシュ値ベースで管理し、シンボリック・リンクを貼り替える）ことで、異なるバージョンのテストやトライ＆エラーをしやすくしています。

また、後述する IPFS、ブロックチェーンや、そのマッシュアップで新型コロナの頃に話題になった NFT などでは要かなめの関数とも言えるなど、ハッシュ関数は、今後もさまざまな場面で活躍が期待される関数です。

この記事では、「ハッシュ関数の基本と基礎知識」、そして「ハッシュ関数を活用した SQLite3 の 1 つのアイデア」をシェアしたいと思います。

_{^{🐒 2021/02/19 追記: Qiita の Markdown の仕様変更により、今まで <details> タグで「必要な人だけみれる」ように隠していた基本的な情報も表に表示されています。そのため、やたら長い記事になっています。

🐒 2021/03/05 追記: Qiita の Markdown で、<details> タグの仕様変更は β 版の一時的なものだったらしいのですが、また再々編成するのも面倒なので、そのまま表示した状態にします。と言うのも、Qiita は編集時に数文字打つたびにプレビューを更新するので、これだけ長文の記事になると秒単位で動作が重くなります。そのため、重複する説明も多く、やたら長い記事のままになっています（近々 git でオープンソースにしようか考えています）。

目次を見て、ハッシュ関数の基本や活用方法は「完全に理解した」と感じた方は、本題の「長さを知ったところで何？」まで、スキップしてください。答えを先に言っちゃうと「データのハッシュ値 n 桁を SQLite3 の rowid に使う」って模索した時の話しです。それでも読んでみようという方は、ゴロ寝でもしながら読んでください。よく寝れると思います。私も書いていて寝ちゃいます。}}

ハッシュ関数を完全に理解した気になるコマケーこと

ハッシュ関数の基本と特徴

先に、一言で恐れずに言うなら「ハッシュ値・はデータの指紋」です。

つまり「データのハッシュ化」と言うのは「データから情報の指紋を採取すること」みたいなもので、データの暗号化でも圧縮でもないのです。

もちろん、データなので指を持ちません。そのため「指紋」よりは、ハッシュ値はデータの「情報紋」と言ってもいいかもしれません。

人間の指紋が特定の個人を識別するために使われるように、データの指紋（ハッシュ値）も特定のデータを識別するのに使われます。

符号化された情報、つまりコンピューターが認識できるデータ（0 と 1 のビットで表現できる情報）であればテキストであろうが、画像であろうが、プログラムであろうが、そのデータからハッシュ値を得ることができます。

人間の指紋は、それ自体からは直接本人を特定できませんし、個人情報を持ちません。しかし、本人の指紋と「比較」したり「対応表」さえあれば、誰の指紋であるか特定できます。そして、そこから DB で個人情報と紐づけることができます。とは言え、本人を特定できたとしても指紋からは本人を復元（クローンを作成）できません。

ハッシュ値も似ています。ハッシュ値だけでは元の値はわかりませんが、ハッシュ値を比較したり、対応表さえあれば元の値を特定できます。また、それをもとに（キーとして）DB に紐づけることもできます。さらに、ハッシュ値を知っていても、ハッシュ値そのものからは元の値を復元できません。

「復元できない」というのは、逆算できない・計算で割り出せないということです。例えば「割り算の余り」（剰余）からは、元の値がわからないのと似ています。

固定長のIDを作る例

$max = 100;     // IDの長さ（最大値は99）
$message = 123; // メッセージを数値化したもの（文字コードなど）
$hash = $message % $max; // 123 を 100 で割った余り（必ず 00 〜 99 の固定長）

print_r($hash); // 23 <-- 余りが 23 になる組み合わせは無限にあるため
                //        message を見つけるには行動学的なアプローチ
                //        が必要になる

そして、同じ指紋を持つ 2 人は必ず 1 ペア以上いる（0 %ではない）ように、異なるデータなのに同じ指紋（ハッシュ値）を持つデータは必ず作れます。_{^{（簡単とは言ってない）}}

先の例で言うと、メッセージが異なっても同じ余りになるようなイメージです。

余りが衝突する例

$secret = 100;

$message = 123;
print_r($message % $secret); // 23

$message = 323;
print_r($message % $secret); // 23

もちろん、実際には、こんな簡単な式は使われません。

しかし、とてつもなく弱いながらも関数化すれば立派な「ハッシュ関数」です。ただ、実用には耐えない「アルゴリズム」と「ハッシュ値の長さ」の、なんちゃってハッシュ関数である、というだけです。

つまり、同じ「データの指紋」を持つ確率や識別の精度が内部のアルゴリズムやハッシュ値の長さに依存する、この「謎の箱」がハッシュ関数です。

では、ハッシュ関数の基本を「正しく」知ろうと Wikipedia を開くも、何を言っているのかわかりません。

ハッシュ関数 @ Wikipedia

これは法律や音楽理論や機械学習などのドキュメントと同じように、「同じプロトコルの人向けのドキュメント」だからです。

例えば、「変数」や「配列」と言う用語がわからないのにソート・アルゴリズムの説明を覗きに行ったり、メモリアドレスやポインタが理解できていないのに高速化ドキュメントを読んだり、ビットや XOR がわからないのに TCP や JPEG の仕様書を覗くようなものです。

もしくは「デスクトップを右クリックしてプロパティを開いてください」と説明したら、「日本語でおk」と相手がブチキレたことはないでしょうか。同じようなものです。

つまり、ハッシュ関数を正しく知ろうとするとプログラミングの基礎だけでなく「数学」や「暗号学」の基礎知識も必要なのです。そして端的に伝えようとすると、ある程度の基礎知識を相手に求めることになるものなのです。

この記事は、ゴロ寝読みでもいいので、一通り読んでから、再度 Wikipedia の記事を読み直してみてると「（読める ... 読めるぞ）」となることを期待しています。

学問こわい（暗号学・数学こわい）

さて「数学や暗号学の基礎知識も必要」とは言ったものの、暗号学の世界は調べれば調べるほど「暗号化・復号」といった世間一般が思うことを超え、いまや「暗号＝セキュリティ」と同義なんだなと痛感します。

そして（数学含む）基礎知識がない人から「本当に安全なのか」「なぜ安全と言えるのだ」と言ったことを説明するには、数式で証明して見せるしかありません。言葉で説明すると、今度は言葉が独りひとり歩きするといった機械学習のエンジニアの方と話している時と似たジレンマを垣間見ます。

言葉の独り歩きと言えば、機械学習のディープラーニング系の話題で「研究者も、なぜそうなるのかわからない」と報道されるのを目にしたことがあると思います。そのため「作ってる本人たちすら理解できない謎の技術」的に思われがちです。

しかし、「わからない」というのは「仕組みはわかっているが、キチガイじみたと言うより、天文学的な組み合わせのパターンを機械にさせているため、なぜその組み合わせにたどり着いたのかがわからない」という略なのです。理解していないわけではないのです。

組み合わせの怖さを知らないという方は、「フカシギおねえさん」「組み合わせ爆発」「巡回セールスマン問題」と言ったキーワードで調べてみてください。

そして「では、仕組みを素人にもわかるように説明せよ。三行で。」みたいな、仕組み（理論や理屈）を理解する気もない、結果だけが欲しいせっかちさんが言うものだから、「なんかわからんけど、すごい」という認知と、AI という言葉が一人歩きして、世間との用語の乖離かいりに悩んでいるそうです。

「AI が〜 AI が〜」と騒ぐのは、機械学習の学者からすると「『なんか知らんけど、時代らしい』というだけで付けた、電気ブランやデジタル・パーマみたいなもんが溢れかえっている」らしいです。

まぁ、確かに時代ではあるのですが、ぶっちゃけ 👌資金がないと、まともな研究やモデル作成はできません。そのため流行ってくれないと予算も出ないし、説明した（正した）ところで動くものだけで、仕組みに興味がない相手に時間を割くのも無駄と言うのが現状らしいです。

我々プログラマーの世界で言えば、「デジタル化」は「符号化であって、電子化のことではない」と思いつつも「デジタル化＝電子化」という世間の認知に流されないといけない歯痒さに似ています。もしくは「（えぇぇ。それはクラウドとチャうヤろ）」といった感じでしょうか。

上記 「デジタル化」は「符号化であって、電子化のことではない」 について、思いのほかカチンときた人が多いみたいで、SNS で「トランジスタも電子制御なんだから電子化と言っても間違いじゃない」という感じのツッコミを数件いただきました。

補足しますが、ここで言う「デジタル化」とはディジット、つまり数えられるくらいまで情報量を落とすことを言います。

アナログ・データの内容が「0b1011」と表現できるなら、囲碁の石を「●◯●●」と並べて置いたり「/-//」と壁に傷をつけても、その数（情報）は過不足なく相手に正確に伝えたり、残すことができるという意味です。同様に、アナログであっても波の幅を「広い・狭い・広い・広い」とさせれば、アナログ信号でデジタル情報を伝えられます（いわゆる地デジ）。

アナログを「坂」だとすると、デジタルは「階段」のようなもので、「なんとか山の●合目で待ってる」より「なんとか山の●段目で待ってる」の方が正確に伝わるイメージでしょうか。

つまり、必ずしも電気もしくは電子機器でないとデジタル化できないというわけではないのです。それらを使った方が、何かと楽だし、速いというだけなのです。

また、「数えられる」という点で「デジタル化」を「量子化」とも言ったりしますが、ことハッシュ関数における説明においては「量子化」という言葉を使うのは好きではありません。後述しますが、ある種のハッシュ関数（特に暗号がらみ）では天敵とも言える量子コンピューターの話で、わけわかめになるからです。同じ「量子」ですが、「佐野量子」くらい違いがあるのに、勝手に紐づける人が多いからです。

この記事では、例えば画像をスキャンしただけのものは「電子化」、画像からデータを抜き出し解釈できるもの（例えば OCR データ）を「デジタル化」と呼びます。これは後述する「電子署名」と「デジタル署名」の違いで重要だからです。

さて、暗号学の世界も我々のようなパンピーが解釈した内容が微妙に間違ったまま広まっているため、動くものだけで仕組みには興味がない相手に、基礎から教えたり間違いを正す時間を割くのも無駄と感じるようです。

偉そうにゆうて、筆者も数学や暗号学に強いわけではありません。

しかも、エンジニアと言うよりは猿人に近いのえんじんにnearなので、1 つの公式より 500 文字のソースコードを見せてもらった方が理解できるのです。

そこで、bash などを触ったり、自分で何かしらのプログラム言語で俺様関数を作ったことがあればわかるプログラマー的な表現方法で「知っておいた方が良いハッシュの基礎知識」を説明したいと思います。

なお、この記事にはサンプル・プログラムはあるものの、計算式やアルゴリズムの詳細はありません。また、セキュリティーの記事でもありません。むしろ暗号学やセキュリティー以前・・の基礎知識レベルです。「割り算の余り」や「変数」が理解できていれば十分です。

あくまでも筆者が考える、実動作するものを通して理解する「ハッシュ関数の基礎きそ概論がいろん」的なものです。そのため、丁寧に説明しているつもりですが、いささかくどい・・・部分があります。

ジャンクフード的な記事ですが、自分なりに「ハッシュ関数が好きになる話題や実例」を、てんこ盛りにしていますので、ゴロ寝でもしながらスマホでお読みください。

この記事では、さまざまな用語と、その概要を説明しています。そして、それらの用語がつながって（点と点が線になって）行くさま・・を楽しんでいただければと思います。

また、興味のあるキーワードが出て来たら自分なりに掘り下げて、より正確なものに堀り下げて欲しいと思います。キーワードの概要を理解した上で各種文献をご覧になると、より理解度が高まった、そんな記事になるといいなと思います。

そして間違いを見つけたら、戻ってきて、こっそりコメント欄に書いていただけると嬉しいです。

また、この記事は「❤︎（旧 LGTM）」が付くたび、その時折で得ている知識や間違いを整理するつもりで更新・修正しています。書き出さないと理解できないサガなので、1 つの情報として気軽にお読みください。

「ハッシュ」の意味と「ハッシュ関数」の定義

さて、ハッシュ関数の説明の前に「ハッシュ」の意味と、この記事における「ハッシュ関数」の定義をしないといけません。

というのも、後述しますが一般的に「ハッシュ関数」という言葉は「暗号学的ハッシュ関数」を暗あんに指していることが多いからです。

そのため「ハッシュ関数のアルゴリズムとして CRC を含めるのは違うんジャマイカ^🔈」と言う方もいると思います。

鋭い。

確かに、CRC はチェック・サムの親戚みたいなものだし、正しくは「ジャメイカ^🔈」です。

しかし、それに固執しすぎるとセキュリティにばかり目が行ってしまい、「ハッシュ」の用語の理解だけでなく、「ハッシュ関数」の利用方法を狭めてしまいます。

特に、「データの類似性」をハッシュ値にする「知覚ハッシュ」（Perceptual Hash）の理解の妨げや、機械学習において「ハッシュ化してトークンを作成する」と言われ「機械学習に暗号が使われている」といった誤解にも繋がりかねません。

「ハッシュ」とは何か

myArray["foo"] = "bar"; などの連想配列の「ハッシュ・テーブル」や、JSON オブジェクトなどの「ハッシュ」（添字配列）と聞いて、「（ハッシュって何だろう）」と調べたら、やたら暗号や数学の話しが出てきて、そっ閉じされた方も多いと思います。

それでは「ハッシュ」とは何でしょう。

ハッシュ関数の「ハッシュ」は「hash」と書き、単純に日本語に訳すと「ごた混ぜ」「細コマ切れ」「台無しにする」などの意味があります。

しかし、その語源を辿ると面白いルーツがわかります。

美術の古典技法で「hatch」という平行線で描画する技法があり、フランス語の「hach^🔈」から来ています。日本の漫画などでもペン画の基本となっている技法ですね。


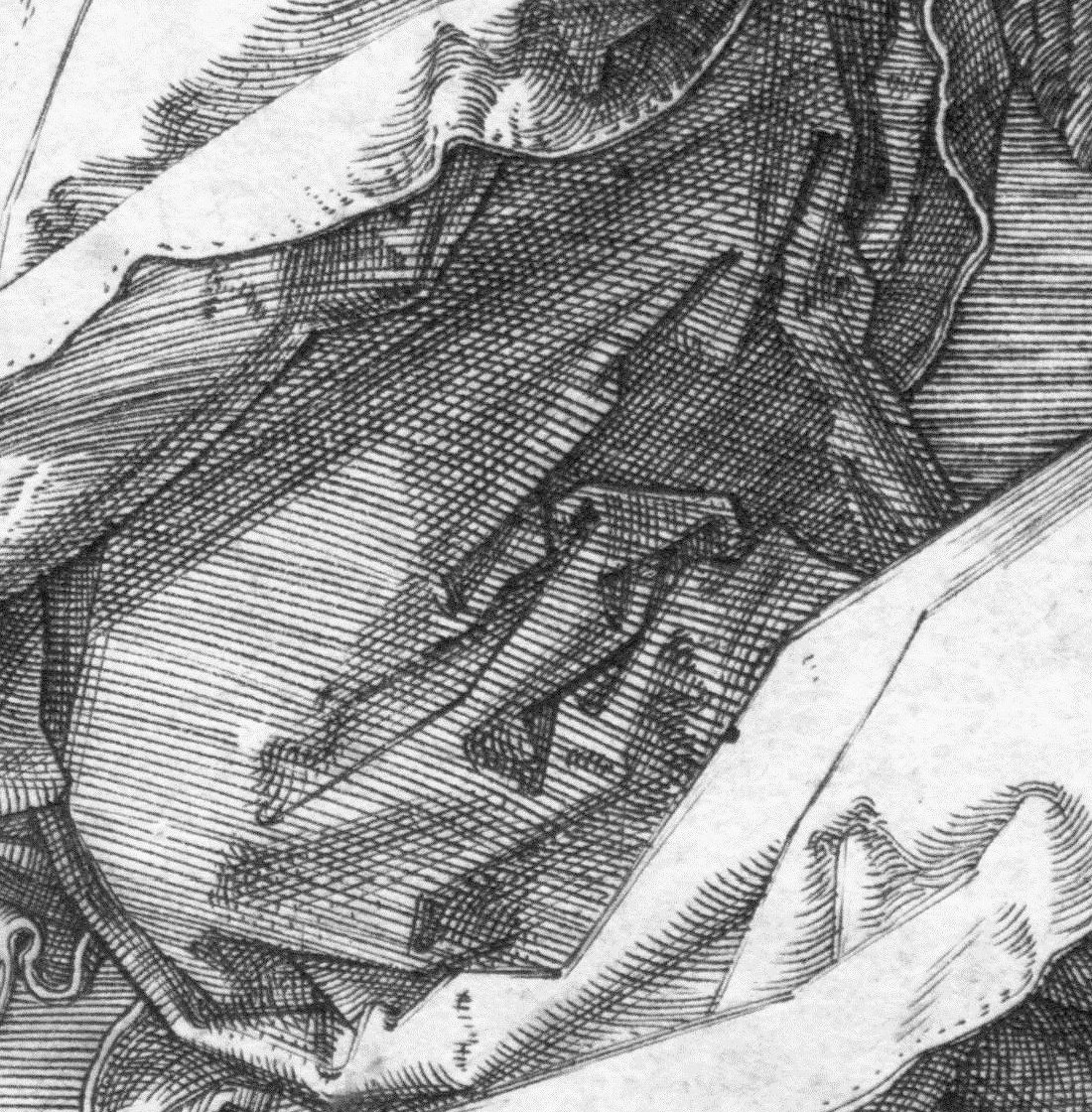ハッチング技法の例（Wikipedia 「ハッチング」より）

諸説あるものの、そこから英国イギリス英語では平行線で構成された「井いの字」や「二にの字」のような状態のものを hatch もしくは hash と呼ぶようになりました。潜水艦や宇宙船の「ハッチを開ける」などのハッチも「井いの字型の出入り口」であったことから来ています。

そして英国では電話の「＃」キーを「ハッシュ・キー」と呼ぶようになりました。これが現在の「ハッシュ・タグ」（ハッシュ記号 ＃ によるタグ付け）の語源です。肉やジャガイモなどを、縦横に井いの字カットしていき、細切れになったものを「hashed 〜（ハッシュドなんとか）」と呼ぶのも同様の語源です。

転じて、データをコマ切れにして、それ単体では全体がわからないものをコンピュータの世界では「ハッシュ」と呼びます。

例えば Javascript などの Hash map や、Redis などの hash といった、どうみても連想配列か JSON のオブジェクトにしか見えないものを「ハッシュ」と呼んでいるのも、データ全体を細分化したものだからです。

ID	Name	Age
001	Alice	32
002	Bob	33
003	Charlie	16

上記データの Redis におけるハッシュ（1 件のデータ。行のこと）。

Key	Value
ID	001
Name	Alice
Age	32

しかし、この程度の細分化では個々のデータを寄せ集めれば元の形に戻ってしまいます。角切りステーキのようなイメージです。ハンバーグのミンチ肉のように、復元ができないレベルまで分割して都合のいいサイズで使いたい場合に使われるのが「ハッシュ関数」です。

🐒 ちなみに「ミンチ肉」などの「ミンチ」は、ラテン語の「小ささ」の意である「minutia」が、フランスで「mincier」になり、英国の「mince」になったものです。「分ふん」の minute や「小さい」の mini がミンチ肉と同じ語源なのも面白いですね。

「ハッシュ関数」の定義

データをコマ切れにするなど、「それ単体では全体がわからないデータをハッシュと呼ぶ」ことはわかりました。

そして、ハッシュ・マップなどは寄せ集めれば全体が見えてしまうので、そもそも元の形に復元ができないレベルまで細分化（ミンチ状態に）して、都合のいいサイズにしたい時に使うのがハッシュ関数ということもわかりました。

以上を踏まえて、この記事における「ハッシュ関数」の用語の定義をしたいと思います。

A hash function is any function that can be used to map data of arbitrary size to fixed-size values.

（Hash Function @ Wikipedia より）

【筆者訳】
ハッシュ関数とは、任意のサイズのデータを固定サイズの値にマッピングするために使用できる関数全般のことを言います。

つまり、どのような内部処理の考え方アルゴリズムの関数であっても「その関数を通すと固定長のデータで返ってくる関数」を、この記事ではハッシュ関数と呼びます。広義（広い意味）でのハッシュ関数ですね。

「ハッシュ関数」とは何か

何はともあれ「ハッシュ関数は、任意のデータを渡すと『ハッシュ値』と呼ばれる値が返ってくる関数のこと」です。

... ... まぁ、そうですよね。

でも「ただの関数である」という認識は意外に重要なのです。

機械学習などで「ニューラル・ネットワーク」とか見聞きする際、「○」がたくさんの線でつながっている図を見て、怖いと感じた方もいると思います。

実は、あの「○」って関数やメソッド（クラス関数）のことなんです。

そして関数の出力を、別の関数の引数に「配列で渡している」のが「線」なんです。

しかも「○」の関数は「引数に重みを付けて足し算してフィルターにかけるだけ」といった「単細胞かよっ！」と言いたくなるような単純な処理をするだけだったりします。

そう考えながら見ると単純です_{^{（簡単とは言ってない）}}。

「ハッシュ関数」も、なんだかんだ言っても結局のところ「ただの関数」なのです。

「函数」つまり「引数が同じなら期待する値が出てくる謎の函はこ」です。そして「ハッシュ値なる謎の値」が戻り値であると言うだけです。（「ハッシュ値」については後述します）

ほとんどのプログラム言語で「ハッシュ関数」は実装されていますが、使用できるアルゴリズム函の中身は環境によって異なります。標準ライブラリ（最初から同梱されているモジュールなど）に含まれているかに依存するからです。

「ハッシュ値」とは何か

さて、ハッシュ関数の戻り値である「ハッシュ値とは何か」の前に、以下の "beef" および "beef1" という文字列をハッシュ値にした例をご覧ください（一見、ランダム関数のようにも思えますが違いは後述します）。

本記事で使用する言語は、bash と PHP です。コマンドが 1 行でおさまると言うだけで選びました。どちらの言語も知らなくても、やっていることは同じなので気楽に構えてください。文字列を関数に渡して出力しているだけです。プログラムの文法などは深く考えずに「単純に何をしているか」に気付けば十分です。

bash は openssl コマンド、PHP では hash() 関数を使ってハッシュ化しています。また、利用するアルゴリズムは md5 と sha512 です。

ポイントは、bash php に限らず、どのプログラム言語を使っても以下の 3 つは同じことに注目です。

数値（16 進数）の文字列で返ってくる。
アルゴリズムと引数が同じ場合は結果も変わらない。
塩を 1 足すだけで結果が大きく変わる。

ハッシュド・ビーフの例

引数が同じなら結果も毎回同じミンチ肉

$ # 粗挽き牛ミンチ
$ echo -n 'beef' | openssl md5
34902903de8d4fee8e6afe868982f0dd

$ # 粗挽き牛ミンチ
$ echo -n 'beef' | openssl md5
34902903de8d4fee8e6afe868982f0dd

言語が違っても同じアルゴリズムと引数なら同じミンチ肉

$ # 粗挽き牛ミンチ（Bash）
$ echo -n 'beef' | openssl md5
34902903de8d4fee8e6afe868982f0dd

$ # 粗挽き牛ミンチ（PHP）
$ php --run 'echo hash("md5", "beef");'
34902903de8d4fee8e6afe868982f0dd

具材を変えてみる

$ # ハッシュド・ポテト
$ echo -n 'poteto' | openssl md5
147f31c730caa77f8a3440e549264a2e

$ # トマト・ペースト
$ echo -n 'tomato' | openssl md5
006f87892f47ef9aa60fa5ed01a440fb

引数を少し変化させる（味付けしてみる）

$ # 粗挽き牛ミンチ ＋ 1g の塩入り（beef1）
$ salt=1; echo -n 'beef'$salt | openssl md5
30017279d6a5bac241e764eeed261dd8

$ # 粗挽き牛ミンチ ＋ 1g の塩入り（コックが違っても同じレシピなら同じ味）
$ php -r '$salt=1; echo hash("md5", "beef" . $salt);'
30017279d6a5bac241e764eeed261dd8

より細かいアルゴリズムに変えてみる

$ # 絹ごし牛ミンチ
$ echo -n 'beef' | openssl sha512
8cd8bb0cef938ef9cd054c2c2cb965e83310ab5c197cb5fc8f35892a44c1a028bac9e1bcd6248580fa2739cc96074885ea3ee116ef35c2d8f6124270aeff50b7

$ # 絹ごし牛ミンチ（コマンドの言語が違っても同じアルゴリズムと引数なら同じミンチ肉）
$ php -r 'echo hash("sha512", "beef");'
8cd8bb0cef938ef9cd054c2c2cb965e83310ab5c197cb5fc8f35892a44c1a028bac9e1bcd6248580fa2739cc96074885ea3ee116ef35c2d8f6124270aeff50b7

$ # 絹ごし牛ミンチ ＋ 1g の塩入り
$ salt=1; echo -n 'beef'$salt | openssl sha512
a528829f370819123ad3fb04d8066b77ec79ce6eddad07e5b2c925bbd9b2e699e73428d23315875c29b45500b8c767262cf5546e33974e4f7a6102abd1bb045e

$ # 絹ごし牛ミンチ ＋ 1g の塩入り（コックが違っても同じレシピなら同じ味）
$ php -r '$salt=1; echo hash("sha512", "beef" . $salt);'
a528829f370819123ad3fb04d8066b77ec79ce6eddad07e5b2c925bbd9b2e699e73428d23315875c29b45500b8c767262cf5546e33974e4f7a6102abd1bb045e

オンラインで動作をみる (PHP, Bash, Go, Python3) @ paiza.IO

Windows の PowerShell でも試してみる

Windows 11 の標準コマンドでハッシュ値を確認するには certutil と Get-FileHash コマンドがあります。

certutil は多機能である（証明書の無効化操作といったクリティカルな機能も含む）ため、単純にファイルのハッシュ値を確認するだけなら Get-FileHash を使うことが推奨されています。

Get-FileHashの構文

Get-FileHash [オプション] <ファイルのパス>

# 使用例
Get-FileHash -Algorithm SHA512 foo.pdf

問題は Get-FileHash は「ファイル」のハッシュ値に特化していることです。そのため、「文字列」のハッシュ値を知りたい場合は直接使えないので、工夫が必要になります。

文字列を一旦ファイルに書き出してから実行

PS C:\Users\KEINOS\OneDrive\Desktop> # 改行なしで "beef" のテキストを作成
PS C:\Users\KEINOS\OneDrive\Desktop> "beef" | Out-File beef.txt
PS C:\Users\KEINOS\OneDrive\Desktop> Get-FileHash -Algorithm MD5 ./beef.txt

Algorithm      Hash                                 Path
---------      ----                                 ----
MD5            34902903DE8D4FEE8E6AFE868982F0DD     C:\Users\KEINOS\OneDrive\Desktop

スクリプト内で文字列をハッシュ化したい場合は、一旦ストリームに文字列を書き込み、ストリーム経由で読み込ませる必要があります。

beef.ps1

PS C:\Users\KEINOS\OneDrive\Desktop> # スクリプトの中身
PS C:\Users\KEINOS\OneDrive\Desktop> get-content ./beef.ps1
$stringAsStream = [System.IO.MemoryStream]::new()
$writer = [System.IO.StreamWriter]::new($stringAsStream)
$writer.write("beef")
$writer.Flush()
$stringAsStream.Position = 0
Get-FileHash -InputStream $stringAsStream -Algorithm MD5 | Select-Object Hash

PS C:\Users\KEINOS\OneDrive\Desktop>　# スクリプトの実行
PS C:\Users\KEINOS\OneDrive\Desktop> . ./beef.ps1

Hash
----
34902903DE8D4FEE8E6AFE868982F0DD

参考文献：「例 4: 文字列のハッシュを計算する」 | Get-FileHash | リファレンス | PowerShell @ learn.microsoft.com

PowerShell 検証バージョン

PS C:\Users\KEINOS\OneDrive\Desktop> $PSVersion::PSVersion

Major  Minor  Patch  PreReleaseLavel  BuildLabel
-----  -----  -----  ---------------  ----------
7      4      1

さて、上記を見ると beef の原型はありませんが、ハッシュ値の対応表があれば、元は beef もしくは beef1 であることは確認できそうです。

ハッシュしたてのビーフはミミズにしか見えませんが、成分表（？）上は同じでも「原型を留めていない状態を数値の文字列にした値」がハッシュ値です。

非可逆な感じは、「覆水盆に返らず」でも「水である」ことはわかるようなイメージでしょうか。

とは言え、ハッシュ値は「値」とあるように数値です。しかし、10 進数の値のままだと人間（エンジニア）が扱いづらいので短くするため、一般的に 16 進数の「数値の文字列」で返してきます。ハッシュ関数のオプションによっては文字列型でなく、バイナリ（バイトデータ型）のまま取得できるものもありますが、いずれにしても「数値として認識できる値」で返ってきます。

そして、どのようにミンチ（ハッシュ）にするかが「アルゴリズム」になります。

カードをシャッフルするかのように何度も XOR をする物もあれば、データを 1 バイトずつ読み込みながらゴニョゴニョしたりと、どのアルゴリズムも使用目的や思想によって設計が異なります。

暗号学的ハッシュ関数とチェックサム的ハッシュ関数

ハッシュ関数の戻り値である「ハッシュ値」を生成するには、本記事の一覧で紹介しているように、色々なアルゴリズムがあります。

各々異なった思想や目的で設計されていますが、いずれのアルゴリズムでも「引数が同じであれば戻り値も同じ」「どんな長さのデータでも固定長のデータにする関数」という点は変わりません（例え演算結果が 1 と短くても、最大値は決まっているため「パディング」と言って、頭をゼロで埋めて固定長にします。それに輪を掛けて、SHA-3 の SHAKE256 のように任意の長さで取得できるアルゴリズム、つまり可変長のアルゴリズムもありますが、引数が同じであれば同じ値が返ってきます）。

「ハッシュ関数」の種類

ハッシュ関数には大きく 2 つの種類があります。

暗号学的ハッシュ関数と、それ以外です。

ハッシュ関数によっては、暗号化にも使われている考え方アルゴリズムを利用したものがあります。これを「暗号学的ハッシュ関数」と呼びます。恐れずに言うと「セキュリティー目的で使われるハッシュ関数のこと」です。

先述しましたが、ハッシュ関数には以下の 2 つの特徴があります。

同じ結果になる: アルゴリズムと引数が同じ場合は、同じハッシュ値が返ってくる。
同じ長さの値になる: ハッシュ値は固定長の数値で返ってくる（一般的に n 桁の HEX 文字列）※1

そして「暗号学的ハッシュ関数」の場合は、これに輪をかけてさらに大きな 3 つの特徴が加わります。

同じハッシュ値にならない: 異なる引数を、同じハッシュ値にするのは限りなく難しい。
逆算ができない: ハッシュ値から元の値（引数の値）は計算式による算出ができない。※2
予測が困難である: 入力の規則性に対して出力に規則性があってはならず、ハッシュ値から元の値の予測は難しい。※2

※1）本記事未掲載である SHAKE256 などの一部のアルゴリズムでは「任意の長さの戻り値が得られる」可変長で返すものがあります。しかし「引数が同じ場合は、戻り値も同じ」と言う点で、同じ引数であれば毎回同じ値、つまり同じ長さで返ってくるのは変わりません。ちなみに SHAKE256 の 256 は出力のビット長ではなく、内部で使われる強度です。
※2）無限ループ（総当たり攻撃）による算出や辞書攻撃による予測の場合除く。逆に言えば「暗号学的ハッシュを利用しない」アルゴリズムは、暗号学的ハッシュと比べ、より予測・衝突可能になります。衝突や暗号学的ハッシュに関しては後述します。

異なる値なのに、ハッシュ化すると同じ値になることを「衝突」（コリジョン）と言います。

しかし、同じ衝突でも「あるハッシュ値と同じハッシュ値になる値を探す」のと「同じハッシュ値になる異なる 2 つの値を探す」のでは種類が違います。

「自分と同じ指紋の人を探す」のと「同じ指紋を持つ 2 人を探す」のでは確認する数が違うのと同じです。研究する上で、これらの違いは重要なため、専門家同士が迅速に疎通できるように各々に専門用語が付いているので Wikipedia や専門記事を読んでも難しく感じるのです。

暗号学的ハッシュ関数について、セキュリティ（暗号学）専門の方の説明を聞いても、わかるようでわからない説明に感じます。「... ... 美学」と説明されるような小難しさです。

「なぜ小難しい言い方をするのだろう」と思い、備忘録として、この記事を書き始めたわけですが、単純に「（その業界の）勉強不足」という語彙力のなさなのでした。とほほ。

まとめると、ユーザー目線だと「暗号学的ハッシュ関数」は、データの改竄かいざん検知に強い「データの同一性」が重視されたハッシュ関数であるのが特徴です。つまり、異なるデータが同じハッシュ値になりづらいアルゴリズムとも言えます。

ランダム関数とハッシュ関数

さて、ハッシュ関数に触れ始めるとランダム関数との違いが気になってきます。

ハッシュ関数とランダム関数は、どちらも戻り値の予測が難しいゴタ混ぜな数値を返します。しかも、ランダム関数（擬似乱数）も、シード値が同じ場合は「毎回同じ結果になる」のです。

ランダム関数は、同じ値になる戻り値を「均等にランダムに返そうとする」ことが目的です。つまり、出力結果に偏りかたよりがないようにランダムに値を出力しようとします。そのため、ランダム性の性能は、OS やライブラリやハードウェアに依存するため、シード値が同じでも、すべての環境で同じ値が返ってくる保証がないのです。

反面、ハッシュ関数の場合は「アルゴリズムと引数が同じなら、どの環境でも毎回同じ結果になる」という点がランダム関数と異なります。

さらに、ハッシュ関数の場合（特に暗号学的ハッシュ関数）は、「入力値が異なるなら、なるべく同じ値の戻り値にならないように返そうとする」点も異なります。

暗号化とハッシュ化

さて、「暗号学的ハッシュ関数」と言われて「暗号学・的？暗号的でなく？」と思った方も多いと思います。

これは、暗号学の考え方を取り入れた、セキュリティ用途に使われるハッシュ関数だからです。

「暗号学的ハッシュ関数」は後から出てきたのですが、現在は他を凌駕りょうがし、ハッシュ関数と言えば暗号学的ハッシュ関数を暗黙的に指すことも多くあります。

ハッシュ関数は「暗号の世界」でも、とてもよく使われる関数で、暗号化する際にも内部でよく使われます。

そのためか、ハッシュ関数を「データを暗号化する関数の一種」のように説明しているブログもありますが、違います。ハッシュ関数自体は暗号化をするものではありません（後述しますが、関連はあります）。

確かに、元データとハッシュ値の対応表を別途用意していれば、対応表を暗号の解読コード表としても使えるため「暗号用途」には使えます。

しかし、暗号は「可逆」、つまり元に戻せる（復号できる）とわかっているから暗号と呼ばれます。

反対にハッシュ関数は「非可逆」、つまり「元には戻せないことが特徴」であるため、ハッシュ化は暗号化ではありません。

くどいのですが、この違いは意外に重要なのです。

と言うのも、ハッシュ関数を知らないし興味もない相手に説明するのが面倒たいへんなため「暗号の一種です」と言ってしまうものだから「ハッシュ値を復号したい」という人が後を断ちません。「ハッシュ化」=「暗号化 + 圧縮」と勘違いさせてしまうパターンです。

これは、「アーカイブ」を「圧縮」と説明されるものだから「tar でアーカイブしたのに、サイズが小さくならない」と勘違いするような、小さなことかもしれません。しかし、そのようなクレームを入れる人は「ハッシュ値から復号して欲しい」と要望するのです。

また、「暗号学的ハッシュ関数」を説明する時に「暗号学的な特性をもたなければいけない」という言葉からも誤解が生まれているようです。

「（暗号の特性ということは復号できるんだな）」と。

できません。

おそらく、大半のハッシュ関数初心者が勘違いすることではないでしょうか。かく言う私もそうでした。

ここで重要な用語の認識があります。「暗号」です。

と言うのも、先に「暗号は復号できる（元に戻せる）とわかっているから暗号と呼ばれます」と言いました。実は、これは「パソコン」を「計算機」と言ってしまうくらいの語弊があります。

現在「暗号」と付くものは「セキュリティ」と同義です。どちらも「何かを他者から守るもの」と考えれば、しっくりくると思います。

つまり、暗号化・復号だけを暗号と呼ぶのではなく、暗号学を駆使したセキュリティ技術も「暗号」と呼ばれます。

例えば、後述するビットコインなどのハッシュ値の塊かたまりみたいなものでも「暗号資産」と呼ぶのも最さいたる例です。

「暗号資産」と言うのは「暗号化された資産」という意味ではなく「暗号学でセキュリティが強化・保護された資産」という意味なのです。ゼロ知識証明などの最先端の暗号技術が駆使されているのです。

「ゼロ知識証明」を恐れずに一言で説明すると「自分が持っている数値を相手に知らせることなく、相手はその値が正しいことを知ることができる技術」です。

例えば、暗号資産における「ゼロ知識証明」は、支払いや振り込みなどで口座の残高を相手（もしくは仲介者）に知らせずとも「必要なぶんの残高はある」と相手に数学的に証明することで取り引きを成立させるものです。

つまり、相手の口座残高に関する知識（情報）がゼロでも、確実に残高があると（数学的に）確信が持てるという点でデビットカードのような取り引きを可能にします。

「んな、アホな。なんか詐欺っぽい」と思うかもしれません。私も思いました。しかし、後述する公開鍵暗号も「自分が持っている数値（秘密鍵）を相手に知らせることなく、相手はその値が正しいことを知ることができる技術」だったりします。

しかも暗号資産は、後述するブロックチェーンにより、これに加えて取り引きの透明性と堅牢性（改竄かいざんへの耐性など）が加わるため、暗号資産の技術は注目を浴びているのです。マスメディアが言うような法定通貨の代替となるからではありません。

そもそも日本において、法定通貨の代わりとなるデジタル通貨は、すでに日常で使われています。V ポイント（旧 T ポイント）、楽天ポイント、d ポイント、Suica といったポイント・システムです。ビットコインと違い、直接現金化（換金）できませんが、既存のポイントシステムの方が（自社システムのため）決済処理も速く、日常の利便性は高いのです。

日本国内でビットコインが日常に浸透しないのは、ドルを普段使いしないのと同じ理由です。すでに信用に足る、高速決済可能なポイントシステムやクレジットなどの独自決済システムが浸透しているためです。沖縄で米ドルが使えるのは、円と同じくらい信用があり利用価値があるからです。

逆に言えば、自国の法廷通貨が信用できないため、金（Gold）や安定した外貨に頼るケースでは、ビットコインなどの暗号資産は普段使いされます。ロシア、中国やエルサルバドルが良い例でしょう。暗号資産が日常の決済手段ではなく、ドルのように為替かわせ寄りの印象があるのはそのためです。

このように、セキュリティに関係したハッシュ関数の使い方も広義の意味で「暗号」の一部だったりします。

そのため、この「現在の暗号の常識」を認識している人が言う「ハッシュ化は暗号の一種です」というのは、実は間違っていないのです。問題は、その常識を認識していない人にも同じように説明してしまうためなのです。

英語であれば cipher、encryption、cryptography は違うものなのですが、日本語に翻訳されるものはすべて「暗号」や「暗号化」と翻訳されるのが問題かもしれません。日本語難しい。

日本語が難しいと言えば、翻訳の問題も「ハッシュ関数が暗号の一種という誤解」に関係があると思います。

暗号の論文をわからないながらも読むと "〜 by one-way encryption using hash ..." という言い方が多く出てきます。

丁寧に訳すと「... の、逆算による復号が難しい暗号化を行うためにハッシュ値で〜する」という意味です。

しかし、基本がわかっている人には長ったらしい説明であるため「一方向暗号をハッシュで行う」みたいに訳してしまうのだと思います。

後述する「一方向性関数」を理解して、じっくりと咀嚼そしゃくすれば訳は間違ってはいないとわかるのですが、パッと「一方向暗号をハッシュで行う」と言われると「ハッシュ関数で一方向に暗号化する」と捉えてしまいそうです（ました）。

また、暗号学の世界では、2 つの固定長のデータを 1 つの非可逆な固定長データとして出力する関数を「One-way compression function」（一方向性圧縮関数）と呼びます。「非可逆な固定長データにする」という点から、これらの関数を「hash function」とも呼ぶことがあるため、「暗号化＋圧縮＝ハッシュ値」と誤解のある説明になりがちなのだと思います。

さて、以上を踏まえると「暗号学的ハッシュ関数」が意味することは「セキュリティ目的で使われるハッシュ関数」と言えます。

とは言っても、以下の条件に「暗号でも使われる考え方」（アルゴリズム）を利用しているハッシュ関数というだけのことです（重要なのですが）。

「A → （処理） → B」としたとき
1. 「B から A がバレてはいけない」
2. 「C から B が作成できてはいけない」

このような「片方向の処理は簡単だが、逆方向は難しい」系の関数（A → B は簡単だが B → A は難しい値を返すもの）を One-Way Function一方向性関数と言います。

「一方向性関数」自体は概念的なもので、具体的にこれ・・というものは存在しません。

例えば「大きな素数を掛け算して自然数を返す」関数などが近いものです。なぜなら、逆の「（大きな値の）自然数から素数を算出する処理」は大変だからです。

他にも「割り算の余り」、つまり剰余（MOD や %）などもよく使われます。なぜなら逆の「余りだけから考えられる元の値の組み合わせ」は無限にあるからです。(A * B) % C = D の場合、D のループするパターンを見れば C は予測できても A B の組み合わせは無限にあります。

bashによる、逆算できないし可能性は無限大だけど、めちゃ衝突する、なんちゃって俺様ハッシュ関数

hash(){
    str="$1" OPTIND=1 # 入力を取得
    prime=257         # 秘密の定数
    sum=0             # 割られる数

    # 入力文字ごとにループ
    while   getopts : na  -"$str"
    do
        ascii="$(printf '%d\n' "'$OPTARG")"   # ASCII コードを 10 進数で取得
        sum=$(( sum + ascii ))                # 割られる数に加算
    done

    h="$(( $(( $sum * $prime )) % 100 ))" # 加算値に秘密の定数を掛けて割った余り
    printf "%s:\t%02d\n" "$str" "$h" # 2 桁で出力 (00〜99)
}

オンラインで動作をみる @ paiza.IO

このように「一方向性関数」の考え方は暗号化の処理には重要です。そしてハッシュ関数も一方向性的な性質を持っているため、暗号処理やセキュリティ関連でも、よく使われるのです。

暗号学的ではないアルゴリズム（破損と類似の検知）

これまでの話しをまとめると、「暗号学的ハッシュ」は他のアルゴリズムと比べて「非可逆性」と「同一性」を重視したアルゴリズムです。つまり、「異なるデータが同じハッシュ値にならないこと」を目的としたタイプと言えます。

逆に「暗号学的ではない・・ハッシュ関数」も数多くあります。

主に、暗号（セキュリティ）目的ではなく「データの状態」を確認するためのものです。例えば、非可逆性や同一性よりも「データが壊れていないかの確認」を目的としたタイプです。

つまり、異なるデータが同じハッシュ値になる可能性が高いことを承知の上で、あくまでも手元のデータが壊れていないかを確認するためのものです。有名なものでは CRC などがあります。

ハッシュ値を「データの指紋」だとすると、暗号学的ハッシュ関数に比べ CRC などは「指紋の種類（渦巻き状、ひづめ状、弓形状、変形状など）の確認しかできない程度のもの」と言えるかもしれません。「渦巻き状であるか」は確実に識別できるも、渦巻き状の指紋の人は多い、みたいなイメージです。

ここで「『壊れてない = 改ざんされていない』とした場合、セキュリティ目的で使用しとるやないかーい」と感じた方もいると思います。鋭い。
シャーペンの芯をドアに挟はさんでおき、割れていたら部屋に入られたと検知できる話しを聞いたことはないでしょうか。「データが壊れていないかの確認」とは、シャーペンの芯が割れていないかと同じです。つまり、それ自体はセキュリティではなく、応用がセキュリティなのです。そのため、セキュリティ（暗号）の世界は奥が深いのです。

他にも「暗号学的ハッシュ関数ではない・・」ものに、aHash, pHash, dHash, wHash, NeuralHash などがあります。

これらは Perceptual Hash（知覚ハッシュ）と呼ばれ、「感覚的に似たようなデータかの確認」を目的としたタイプです。

つまり、データの破損や完全な同一性の確認よりも、データの特徴・パターンをハッシュ値にすることで似たようなデータは近い数値、もしくは似たビットの並びになるのが「知覚ハッシュ」です。

知覚ハッシュは、主に画像や音楽といったマルチメディア関連の類似コンテンツの検知に使われます。他にも、最近では「類似論文の検出」や、機械学習において「類似データの生成や推論にも使えないか」といった研究も盛んです。

例えば LLM などでは、単語や語句の関連性を空間軸として、単語や語句を多次元空間に配置します。


_{^{"Word embeddings and how they vary" @ ミシガン大学 AI ラボより}}

すると、類似した文は類似した関係値を持つことになります。その関係値をマッピングしたもの（ハッシュ値とは言わず、Embeddings と呼ばれる配列データ）を、DB の検索キーとしてコンテンツの自然文検索（Semantic Search）に活用したりしています。

知覚ハッシュの具体例として、類似画像の検知で有名な pHash を実際に見てみるとピンとくるかもしれません。

以下の 3 つの画像は人間が見ると「似たようなデータ」です。しかし、暗号学的ハッシュやチェックサム的ハッシュの場合は、1 ビットでも異なるとまったく異なるハッシュ値になります。


MD5: 1776fb44ba995fff55ef3498f289b3ba	MD5: abd3a65a92022c0b1cb37b1d5bafb53e	MD5: 060eeab60cc578367f8cd22731a5774e

対して、Perceptual Hash（知覚ハッシュ）はデータの類似性をハッシュ値にする（数値化する）試みです。例えば、先の画像を 64bit長（16桁）の pHash に通した場合、以下のように同じハッシュ値になります。


pHash-64: ab85f430d0c3d35e	pHash-64: ab85f430d0c3d35e	pHash-64: ab85f430d0c3d35e

また、解像度（出力ビット長）を高めると、違いは出てくるものの、ほぼ似た値になります。


pHash-256: `abfd856df40a30b7` `d081c3e0d2745e0a` `8f56cc0783c35c1f` `8e9b3cf8926d36e8`	pHash-256: `abfd856df40a30b7` `d083c3e0d2745e0a` `8f56cc0783c35c1f 8e993cf8926d36e8`	pHash-256: `abfd856df40a30b7` `d081c3e0d2745e0a` `8f56cc0783c35c1f` `8e9b3cf8926d36e8`

Go言語で実装を見る

package main

import (
	"fmt"
	"image"
	"image/jpeg"
	"os"

	"github.com/corona10/goimagehash"
)

const (
	file1         = "qiitan_color1.jpg"
	file2         = "qiitan_color2.jpg"
	file3         = "qiitan_mono.jpg"
	imgShrinkSize = 8 // 8 -> 64bit pHash, 16 -> 256bit pHash, must be 2^N
)

func main() {
	img1, err := getImg(file1)
	panicOnError(err)

	img2, err := getImg(file2)
	panicOnError(err)

	img3, err := getImg(file3)
	panicOnError(err)

	hash1, err := goimagehash.ExtPerceptionHash(img1, imgShrinkSize, imgShrinkSize)
	panicOnError(err)

	hash2, err := goimagehash.ExtPerceptionHash(img2, imgShrinkSize, imgShrinkSize)
	panicOnError(err)

	hash3, err := goimagehash.ExtPerceptionHash(img3, imgShrinkSize, imgShrinkSize)
	panicOnError(err)

	fmt.Printf("hash1: %x\n", hash1.GetHash())
	fmt.Printf("hash2: %x\n", hash2.GetHash())
	fmt.Printf("hash3: %x\n", hash3.GetHash())
}

func getImg(imgPath string) (image.Image, error) {
	file1, err := os.Open(imgPath)
	if err != nil {
		return nil, err
	}

	defer file1.Close()

	return jpeg.Decode(file1)
}

func panicOnError(err error) {
	if err != nil {
		panic(err)
	}
}

さて、この pHash の仕組みをザクっと説明すると「画像をモノクロ（グレースケール）に変換して、中央値からの濃淡の変化をパターンにし、固定長の配列にマッピングしたもの」です。

とは言え、単純に低解像度のモノクロ・モザイク画像を配列にしたものではありません。JPEG や MP3 の圧縮などでも使われる、差分の違いをパターン化するアルゴリズムを使っています。

ここで言う「パターン化」とは、数値の変化を波と見なし「複数の波が組み合わさったもの」として、単純な波（サイン波）に分解することを言います。そして各々の波の成分をマッピングしたものをハッシュ値とします。

伝わるかわかりませんが、電子音楽で言うシンセ音源と逆のことをするイメージです。各々のオシレーターの設定値（パラメーター）をマッピングしたようなもの、みたいな。もしくはフーリエ変換ってやつです。

そして、どれだけ類似しているかをハミング距離で計測します。

ハミング距離というのは、同じ長さの 2 つのデータを比較した時、違いが少ないほど距離が近い（類似している）とする考え方です。

具体的には、並びの違う箇所の数を距離とします。例えば、2 つのハッシュ値を xor した値（2 つが異なる場合は 1 にする処理）のビットの数を数え、1 の出現数が少ないほど距離が近いと考えます。

go によるハミング距離の実装例

func HammingDistance(a, b []uint64) (int, error) {
	if len(a) != len(b) {
		return -1, errors.New("different length of input")
	}

	dist := 0

	for i := range a {
		// (a xor b) した結果のビットが 1 の数を加える
		dist += bits.OnesCount64(a[i] ^ b[i])
	}

	return dist, nil
}

IMG1	IMG2	IMG3	IMG4

pHash-256: abfd856df40a30b7 d081c3e0d2745e0a 8f56cc0783c35c1f 8e9b3cf8926d36e8	pHash-256: abfd856df40a30b7 d083c3e0d2745e0a 8f56cc0783c35c1f 8e993cf8926d36e8	pHash-256: abfd856df40a30b7 d081c3e0d2745e0a 8f56cc0783c35c1f 8e9b3cf8926d36e8	pHash-256: e6bac719ba453ae6 e4123961c1ae319e 92f063b6c79064f9 c647b6d0924f6666
IMG1 との距離: 0	IMG1 との距離: 2	IMG1 との距離: 0	IMG1 との距離: 122

Go のソースコードをみる

main.go

package main

import (
	"errors"
	"fmt"
	"image"
	"image/jpeg"
	"math/bits"
	"os"

	"github.com/corona10/goimagehash"
)

const (
	file1         = "qiitan_color1.jpg"
	file2         = "qiitan_color2.jpg"
	file3         = "qiitan_mono.jpg"
	file4         = "keinos_logo.jpg"
	imgShrinkSize = 16 // 8 -> 64bit pHash, 16 -> 256bit pHash, must be 2^N
)

func main() {
	images := []string{file1, file2, file3, file4}

	lenImages := len(images)
	hashes := make([][]uint64, lenImages)

	for index, imgPath := range images {
		img, err := getImg(imgPath)
		panicOnError(err)

		pHashed, err := goimagehash.ExtPerceptionHash(img, imgShrinkSize, imgShrinkSize)
		panicOnError(err)

		hashes[index] = pHashed.GetHash()
		fmt.Printf("hash #%d: %x\n", index, hashes[index])
	}

	for i := range lenImages {
		for j := range lenImages {
			if i == j {
				continue
			}

			dist, err := HammingDistance(hashes[i], hashes[j])
			panicOnError(err)

			fmt.Printf("Distance between #%d and #%d: %d\n", i, j, dist)
		}
	}
}

func HammingDistance(a, b []uint64) (int, error) {
	if len(a) != len(b) {
		return -1, errors.New("different length of hashes")
	}

	dist := 0

	for i := range a {
		dist += bits.OnesCount64(a[i] ^ b[i])
	}

	return dist, nil
}

func getImg(imgPath string) (image.Image, error) {
	file1, err := os.Open(imgPath)
	if err != nil {
		return nil, err
	}

	defer file1.Close()

	return jpeg.Decode(file1)
}

func panicOnError(err error) {
	if err != nil {
		panic(err)
	}
}

ちなみに、類似画像のハッシュについて、英語ですが以下の動画が参考になります。

SPED Talk Image Hashing @ Youtube
論文: AN IMAGE SIGNATURE FOR ANY KIND OF IMAGE | PDF by パロアルト研究所 @ ペンシルベニア州立大学
- 論文の説明動画: Ryan Henderson - One in a billion: finding matching images in very large corpora @ Youtube

何はともあれ、いずれのハッシュ・アルゴリズムであっても「データを特定する指紋のようなもの」であることがポイントです。

破損チェック

先に述べた CRC や fnv などの「データが壊れていないかの確認」に使われる値は「チェックサム」とも呼ばれます。

しかし、学術的には「CRC」と「チェックサム」は別物です。各々のアルゴリズムが存在するからです。面倒臭いのが、実用面でチェックディジット的に使われる値全般を「チェックサム」と呼ぶことがあることです。

チェックディジットというのは、例えば、バーコードの最後の 1 桁の数値（ディジット）などです。


データは“123”、チェックディジットは“6”のバーコード（「チェックディジットとは」バーコードのしくみ @ キーエンスより）

上の例では、バーコード・リーダーは値 "1236" を読み取ると「最後の 1 桁を除く値（ここでは "123"）をゴニョゴニョと計算したら最後の 1 桁（ここでは "6"）と同じになるか」と確認することで正常に読み取れたか確認します。

他にも、身近なところではクレジット・カードの番号にもチェックデジットが付いています。カード自体が有効であるかを確認する前に、そもそも入力された（読み取った）番号が正常に読み取れたか確認する必要があるからです。カード会社によってチェックに使われるアルゴリズムは異なりますが、有名なところでは Luhn アルゴリズムがあります。

Go で Luhn アルゴリズムの動作を見てみる @ Go Playground

このように、最後の数値、つまり読み取りエラーを検知するのに使われる数値がチェックディジットです。

そして、ハッシュ値を似たような目的のために使われる場合に「チェックサム」と呼ばれることがあります（「SHA-256 なのにチェックサム足し算って、なぜに？」と思ったことがある人は多いのではないでしょうか）。

そのため、アルゴリズムとしての「チェックサム」と、用途としての「チェックサム」があることに注意します。この記事では CRC およびチェックサムの両アルゴリズムを「チェックサム的・アルゴリズム」と総称します。

なお、暗号学的アルゴリズムに比べ、チェックサム的アルゴリズムは速いものの、改竄かいざんに弱く、パターンが表れやすい傾向があります。

特に改竄に対しては、とてつもなく弱いです。

異なる値なのに簡単に衝突させる（同じハッシュ値にさせる）ことができてしまいます。これは、意図しないコードを差し込むことができるということでもあります。

例えば「foo」というコードに「this is a bad code」というコードを差し込みつつ、「0x1ff172ec」という調整を加えることで、同じハッシュ値にすることができてしまいます。

package main

import (
	"fmt"
	"hash/crc32"
)

func main() {
	// Expected code
	goodCode := "foo"
	hashGolden := crc32.ChecksumIEEE([]byte(goodCode))
	fmt.Printf("Good: %x\n", hashGolden)

	// Inject malicious code "this is a bad code" with adjustment value
	badCode := goodCode + "\nthis is a bad code\n\x1f\xf1r\xec"
	hashHacked := crc32.ChecksumIEEE([]byte(badCode))
	fmt.Printf("Bad : %x\n", hashHacked)
	//
	// Output:
	// Good: 8c736521
	// Bad : 8c736521
}

オンラインで動作を見る @ GoPlayground

これは、チェックサム的アルゴリズムが「たとえ演算結果から元のデータは逆算できなかったとしても、データの改竄がしやすい」と言うことです。

つまり、ハッシュ値のやりとりを傍受された場合に、内容は分からずとも「はは〜ん」と流れを読まれ、いじられてしまう可能性がある、と言うことでもあります。

そのため「流れてきたデータに問題はないか」の確認に、「破損チェック」にはチェックサム的アルゴリズムを使い、「改竄チェック」には暗号学的アルゴリズムを使う、といった特徴に合わせた適材適所の判断が必要になります。

とは言え「数マイクロ秒の差が売り上げに大きく影響する」など、よほどシビアな条件でない限り、暗号学的アルゴリズムを使うのがいいでしょう。暗号学的アルゴリズムはチェックサムとしても使えるからです。（逆はできない）

使うなら SHA-2 系の SHA-512 や SHA-3 系の SHA3-256 などの強めのアルゴリズムなら、なおベストです。処理時間などのコストが許す限りベターなものを選びましょう。組み上がってからベストなものに調整して行った方がいいと思います。便利で丁度いいサイズの MD5 アルゴリズムを大事な局面で使っていると暗号警察がやってきますよ。

CRC をハッシュ関数のアルゴリズムに含める理由

この記事で CRC などのチェック・サム的アルゴリズムを、ハッシュ関数のアルゴリズムに含めた理由ですが、単純に List of Hash Functions に含まれており、たいていのプログラミング言語のハッシュ関数が使うモジュールに含まれているからです。

List of Hash Functions @ Wikipedia

ここで先の「チェックサム的ハッシュ関数はハッシュと呼んでいいのか問題」が出てきます。つまり「CRC やチェックサムはハッシュではない」と言う話しです。

CRC が「ハッシュではない」と言われる主な理由に 2 つあります。

CRC は多項式で足したり XOR しただけの値だから「予測困難」とは言えない。
CRC は「誤り検出訂正」にも使えるので、元に戻せるから「逆算不可」とは言えない。

暗号学的ハッシュと比べパターンが現れやすいことから、最初の「予測困難とは言えない」はわかります。次に 2 の「誤り検出訂正に使える」ですが、「ん？訂正」と思われるかも知れません。

CRC は Cyclic Redundancy Check（巡回冗長検査）の略です。つまり Check（検査）とあるため、誤りを「検出」するためのもので「訂正」には使えないと重いコンダラ状態だったのですが、なんと訂正にも使えるそうです。

Bitfilters | Mathematics of Cyclic Redundancy Checks @ Wikipedia

_{^{🐒 ちなみに「誤り検出訂正」ですが、コンピュータではデータが壊れていた場合に自動修復する機能が、そこかしこで使われています。例えば CD や HDD の読み込みや通信のパケットなどです。英語なのですが、以下の動画が基本的な考え方をわかりやすく説明しています。}}

_{^{Hamming codes and error correction | 3Blue1Brown @ YouToube（英語）}}
- _{^{ハミング符号 @ Wikipedia（日本語）}}

しかし、これはデータを修復する時に CRC のアルゴリズム（考え方）が使えることがあるだけで、「CRC のアルゴリズムでハッシュ化する」のとは根本的に目的が違います。

そうすると、次に「いや、そもそもチェックサムなんだからハッシュとは言えない」と言う、最初の議論が出てきます。

これは「学術寄りの正しい目線」と「一般定義されたユーザ目線」の違いのようなものです。なぜなら、確かに厳密な意味では CRC の値はハッシュ値ではないからです。この議論は、海外の掲示板や SNS でもしばし見受けられます。

しかし、これはプログラムで言う「文字列データ」と「バイナリ・データ」の違いを「文字列だってバイナリだから」と言う議論や、「ランダムと言ってもランダムではない」と言った議論と似た性質を持っています。ユーザーと、内部（の仕組み）を知るものの間での食い違いです。

「ドローンの研究をしています」と言っているのに「ラジコンの研究をしてるんですって」とか言われたり、「モニタと睨にらめっこ」してるのに「テレビばかり見てる」と言われれば、正したくなると思います。どうやら、専門家から見れば、それくらいのモヤモヤ感がある違いらしいのです。

いまどき CRC なんて使い所あるの？

SHA-2 や SHA-3 などのツヨツヨなハッシュ・アルゴリズムを知ってしまうと、CRC などのチェックサム的アルゴリズムなんかオワコンと思われがちです。

ところが、意外なところで使われるのがデーターベース（以下 DB）の負荷分散処理です。

例えば、リクエストされたキー（key）に対してバリュー（value）を返すだけの連想配列のような、キー・バリュー型の DB では、負荷を分散するために使われます。

と言うのも、リクエスト数やデータ量が多くなった場合、複数のノードにデータを分ける必要が出てきます（ここで言うノードとは、複数台で 1 つのサービスを提供している場合の 1 台のことです）。

この時、どの DB ノードにデータを保存するか・リクエストするかを決めるのに、リクエストされたキーをハッシュ関数に通し、その値をノードの台数で割った余り（余剰、mod）を使います。

nodeCount = 3                    // 3台の DB ノードでクラスタリングする
nodeID  = crc16(key) % nodeCount // 0〜2 の ID に分けられる

リクエスト毎に接続先を順番に切り替えるラウンドロビン方式を発展させた考え方で、リクエスト・キーが同じなら決まったノードに転送できます。メリットとしては、ラウンドロビンのように全てのノードが同じデータを持つ必要がありません。

しかし、このままだとノードの増減にフレキシブルに対応できないので、ノードに複数の ID をあらかじめマッピングしておきます。そして、ノードが増えたらマッピングしたデータの一部を移動させます。この考え方を利用した、有名なところでは Redis などがあります。

Overview of Redis Cluster main components | docs @ redis.io

「ハッシュ値」と「暗号」の関係

さて「ハッシュ化は暗号化ではない」とは言ったもののハッシュ値は暗号と密に関係しています。

これは、ハッシュ値は暗号データの担保情報としても使われるためです。

特に暗号通信においては「切っても切れない関係」にあります。公開鍵・秘密鍵暗号では、公開鍵を担保する情報としても使われるからです。他にも、後述しますが、お互いの秘密鍵を共有せずに相手の公開鍵から共通の鍵を作成する際にも、ハッシュ関数が活用されたりします。

🐒 【余談】「公開鍵・秘密鍵暗号」とは

^{「公開鍵・秘密鍵暗号」とは、ペアとなる A と B の２つの鍵があり、片方の鍵で暗号化したものは、もう片方の鍵でしか復号できないタイプの暗号です。

　つまり A 鍵で暗号化したものは同じ A 鍵では復号できません。ペアとなる B 鍵でしか復号できません。また、その逆もしかり・・・です。

　この特徴により、片方の鍵を公開しておき、その公開している鍵で相手に暗号化してもらえれば、もう片方の鍵を持つものでなければ復号できないデータが作れます。鍵を公開してるのに、安全に暗号通信やファイルのやりとりが行える魔法が使えます。鍵を公開してるのに、です。

　ちなみに「鍵」とは、実質的に、いわゆるパスワードと同じ役割をするものです。ワード（単語）ではなく、覚えられないくらいの長い不規則な文字列、もしくはそれをファイルにしたものを「鍵」と呼びます。そして一般的なパスワードとの違いは自分で決められるものではないことです。伝わるかわかりませんが、「復活の呪文」をファイルに落としたようなものです。（具体的な鍵の例 @ GitHub）

　しかし、本質的には「〜のカギとなる」や「キーポイント」のように「重要な部分を引き出すもの」を「鍵KEY」と言います。配列の「key」（鍵）なども、「value」（価値）を引き出す同様の意味です。そのため「鍵」という単語が出てきたら「暗号関連」と言う思い込みを捨てて「キー鍵がないと値が引き出せないもの」と考えるようにしましょう。

　さて、公開鍵・秘密鍵暗号で重要なのが A 鍵と B 鍵は「親」と「子」の関係になっていることです。「親の鍵」からは同じ「子の鍵」は何度でも作成できますが、その逆（子から親の鍵）は作成できません。

　そのため「親」の鍵で暗号化したデータは同じ「親」の鍵では復号できませんが、復号に必要な「子」は作れてしまうということです。つまり、ユーザーは「親の鍵」さえ大切に保管しておけばよく、必要な時に「子の鍵」を作成し、外部に「子の鍵」を公開するのが一般的です。

　このことから親の鍵を「秘密鍵」、子となる鍵を「公開鍵」と呼びます。秘密鍵は「シークレット・キーSecret Key」もしくは「プライベート・キーPrivate Key」、そして公開鍵は「パブリック・キーPublic Key」とも呼ばれます。

　注意点として、「秘密鍵」「公開鍵」は必ずしも暗号化・復号に使うための鍵を指すわけではありません。

　「value」（価値）を引き出すのに必要な「key」（鍵）のうち、公開するものを「公開鍵」、公開してはいけないものを「秘密鍵」と言います。暗号化に使わないものでも、秘密鍵や公開鍵が存在します。例えば署名鍵などです。たまたま、暗号化に使う鍵も著名に使えるというだけです。

　そのため、公開鍵暗号と言いながらも、片方の鍵で署名したものは、もう片方の鍵でしか検証ができないタイプの暗号（セキュリティ）技術も「公開鍵暗号」の 1 つです。

　さて、俗に言う「データの暗号化」ですが、「公開鍵で暗号化」し「秘密鍵で復号する」といった説明の記事が多いのですが、暗号化自体はどちらの鍵でもできますし、反対の鍵で復号できます。　アプリから見れば、鍵が違うだけで、やっていることは復号というだけです。

　とは言え、自分の秘密鍵でデータを暗号化しても公開鍵が一般に公開されている以上、誰でも公開鍵で復号できてしまう時点で、セキュリティとしては「何の対策にもなっていない」と同義です。つまり、データサイズが無駄に大きい、素人にはオススメできないファイルができるだけです。そういった意味で「公開鍵で暗号化」し「秘密鍵で復号する」といった説明がされているのです。

　それでは「公開鍵を一般公開せずに、安全な方法で相手に渡せば」という場合は、やっていることは共通鍵暗号と変わりません。つまり、共通鍵暗号を使った方が復号も速く、データも軽く済みます。

　「この世の全てを、そこにおいてきた」と、秘密鍵で暗号化したお宝の公開鍵をどこかに隠しておき、ネットの海を航海させるような場合にしか効果はないでしょう。その場合であれば、共通鍵のように、お宝を入れ替えて同じ共通鍵で再暗号化されることはないからです。

　不特定多数ではなく特定の相手であれば、もうひと工夫することでセキュリティ的な対策に変貌します。

　それは、「二重に暗号化すること」です。つまり、自分の秘密鍵で暗号化したデータを、さらに相手の公開鍵で暗号化するのです。これの何が「セキュリティ的な対策」になるかと言うと、相手は自身の秘密鍵で復号したのち、送信者の公開鍵でさらに復号することで、確実に 2 者間に限定した暗号データをやりとりできます。逆に、単純に「自分が保証したデータである」ことを公言（証明）したいのであれば、秘密鍵で署名する方が効果的でしょう。

　さて、この２つの鍵（公開鍵と秘密鍵）ですが、一般的（？）な方法として素数の概念が活用されています。

　例えば、自然数 15 を素因数分解すると 3 と 5 です。しかし、3 という数からは 15 はわかりません。3 の素数を持つ自然数（正確には合成数）は無限にあるからです。また、同様に 5 からも 15 はわかりませんが、3 と 5 からは 15 が簡単にわかったり、15 と 3 からは 5 が作成できるような考え方から、さらに工夫されています。もちろん他のアルゴリズムもあり、どれも難しすぎてわかりません。

　しかし「公開鍵・秘密鍵暗号」は欠点も持っています。「大きなデータの暗号化が苦手」なのと「遅い」ことです。特に大きなデータを暗号化する場合は、データをチャンク（ぶつ切り）にしてから各々を個別に暗号化して 1 つにくっ付ける必要があり、復号も逆の手順が必要であるため結構なコストが発生します。サイズも必要以上に大きくなります。

　逆に従来の１つのパスワード（鍵）で暗号化および復号できる暗号方式を「共通鍵暗号」と呼びます。決して「共通鍵暗号」がオワコンと言うわけではありません。

　「共通鍵暗号」は強いアルゴリズムでも処理速度が速く、「公開鍵・秘密鍵暗号」と比べデータサイズが小さいという特徴があります。現在では、大きなファイルの復号や、復号に速度が求められる場合は「共通鍵暗号」で暗号化し、その共通鍵を「公開鍵・秘密鍵暗号でやりとりしておく」もしくは「お互いが相手の公開鍵と自身の秘密鍵から生成する」というハイブリッドな手法が多くとられます。

　暗号の話し自体は、この記事のスコープ（範囲）から外れるため、興味を持たれた方は以下の記事が勉強になります。}

2つの公開鍵暗号(公開鍵暗号の基礎知識） @ Qiita

さて、このハッシュ関数の「非可逆」な特徴は、一般的に「パスワードの保存」などに使われます。

「パスワードの管理」で、皆が通る道に「パスワードをどうやって保存するか」の葛藤があります。

ユーザーのパスワードを生で保存する（そのまま保存する）のはもってのほか。暗号化するにしても秘密鍵が漏洩したら全てのパスワードがわかってしまうため元も子もありません。また、各々のパスワードに対して秘密鍵を作成しても、秘密鍵の DB が漏洩したら同じことです。

しかし、管理側で求められるのは「ユーザーが事前に決めたパスワード」と「ログインで入力されたパスワード」が同じであるかの確認だけです。

「パスワードはサーバーに保存しておきたくない」、でも「パスワードが登録したものと同じか確認したい」という、覚えたくないけど答えられるようになりたい暗記パンみたいなワガママをハッシュ関数は実現します。

具体的には「パスワードをハッシュ化して保存する」ことで可能です。

パスワードが正しいかの確認はハッシュ値を比較すれば良く、「ハッシュ値が流出したとしても元のパスワードはわからない」だけでなく「管理者すら元のパスワードはわからない」といったメリットがあるからです。パスワード流出事件があると「自分たちでもわからない状態で保存されているから云々うんぬん」という話しがでるのもこのためです。

このようなエンコード（特定のルールに従って変換）した値でやりとりする仕組み、つまりオリジナルを隠蔽したままの（デコードする必要のない）状態で、確認のやりとりをする仕組みを「一方向暗号」と呼んだりします。しかし、あくまでもハッシュ値を「暗号セキュリティ用途」として使っているだけです。繰り返しますが、ハッシュ化=暗号化ではありません。

しかし、単純にハッシュ化したからといって安心はできません。

まず、ハッシュ関数のアルゴリズムに CRC のようなチェックサム的アルゴリズムを使ってしまうと、簡単に衝突する（異なるパスワードなのに同じハッシュ値になりやすい）だけでなく、わざと衝突させて改竄する攻撃にまったく耐性がありません。

そのため、後述する salt（塩）を使ったテクニックも役に立ちません。しかし、CRC や checksum は改竄耐性がない以前に、そもそも用途が違います。

次に、「鳩の巣原理」という「鳩の巣箱が鳩の数より少ない場合は、必ず 1 つ以上の巣箱で衝突する鳩がいる」という原理があります。椅子取りゲーム的なものです。

つまり、ハッシュ値のビット長が短かいほど、同じ原理で衝突しやすくなります。

では「暗号学的ハッシュ関数など、ハッシュ値のビット長が長ければ安心か」と言うと、安心できません。

「誕生日のパラドックス」と呼ばれる、「意外に衝突する」というジレンマの問題。
暗号学的アルゴリズムであっても MD5 や SHA-1 のように「合理的に衝突させる方法が見つかっているアルゴリズム」がある。

実は、上記以上の問題があります。

「引数が同じ場合は戻り値も同じ」という、もう１つのハッシュ関数の特徴により流出したデータがハッシュ化されていても意味をなさないことがあるからです。

具体的には、別途パスワード・リストなどがあった場合です。

なぜならパスワード・リストからパスワードをハッシュ化して同じ値を探せばいいからです。つまり「辞書攻撃が使える」ということにもなります。

例えば Folding@home で有名な、バークレー大学の BOINC を使った分散コンピューティングのプロジェクトの 1 つに "Free Rainbow Tables" というものがあります。

これは、注意喚起のために作成された、ハッシュ関数の逆引きを可能とする、数テラバイト規模の巨大な辞書（レインボーテーブル）です。

他にも、過去に流出したメールアドレスとパスワード、32 億件をアーカイブした COMB データなども存在し、その後の流出したものを含めると 150 億件以上のデータが検索可能となっています。つまり、全世界の人口（80億）の約 2 倍近くのパスワードが「表の世界」であっても確認できることになります。

例えば、この記事のサンプルに出てくる 34902903de8d4fee8e6afe868982f0dd（beef を MD5 でハッシュ化したもの）でも、筆者のショボいマシンでも 10 秒以内で総当たり解析できてしまいます。

HashCat を使って34902903de8d4fee8e6afe868982f0ddを解析する

HashCat はオープンソースのパスワード・リカバリー・ツールです。用語ファイルを使った解析だけでなく、総当たりによる解析機能を持っています。
下部で 34902903de8d4fee8e6afe868982f0dd:beef と解析できていることに注目ください。

$ # 総当たり（-a 3)で MD5(-m 0)を解析する
$ time hashcat -a 3 -m 0 "34902903de8d4fee8e6afe868982f0dd"
hashcat (v6.2.6) starting

METAL API (Metal 263.9)
=======================
* Device #1: Intel(R) Iris(TM) Graphics 6100, skipped

OpenCL API (OpenCL 1.2 (Aug 17 2023 05:46:30)) - Platform #1 [Apple]
====================================================================
* Device #2: Intel(R) Core(TM) i5-5257U CPU @ 2.70GHz, 4064/8192 MB (1024 MB allocatable), 4MCU
* Device #3: Intel(R) Iris(TM) Graphics 6100, skipped

Minimum password length supported by kernel: 0
Maximum password length supported by kernel: 256

Hashes: 1 digests; 1 unique digests, 1 unique salts
Bitmaps: 16 bits, 65536 entries, 0x0000ffff mask, 262144 bytes, 5/13 rotates

Optimizers applied:
* Zero-Byte
* Early-Skip
* Not-Salted
* Not-Iterated
* Single-Hash
* Single-Salt
* Brute-Force
* Raw-Hash

ATTENTION! Pure (unoptimized) backend kernels selected.
Pure kernels can crack longer passwords, but drastically reduce performance.
If you want to switch to optimized kernels, append -O to your commandline.
See the above message to find out about the exact limits.

Watchdog: Temperature abort trigger set to 100c

Host memory required for this attack: 1 MB

The wordlist or mask that you are using is too small.
This means that hashcat cannot use the full parallel power of your device(s).
Unless you supply more work, your cracking speed will drop.
For tips on supplying more work, see: https://hashcat.net/faq/morework

Approaching final keyspace - workload adjusted.           

Session..........: hashcat                                
Status...........: Exhausted
Hash.Mode........: 0 (MD5)
Hash.Target......: 34902903de8d4fee8e6afe868982f0dd
Time.Started.....: Sun Mar 24 15:29:11 2024 (0 secs)
Time.Estimated...: Sun Mar 24 15:29:11 2024 (0 secs)
Kernel.Feature...: Pure Kernel
Guess.Mask.......: ?1 [1]
Guess.Charset....: -1 ?l?d?u, -2 ?l?d, -3 ?l?d*!$@_, -4 Undefined 
Guess.Queue......: 1/15 (6.67%)
Speed.#2.........:   313.1 kH/s (0.01ms) @ Accel:512 Loops:62 Thr:1 Vec:4
Recovered........: 0/1 (0.00%) Digests (total), 0/1 (0.00%) Digests (new)
Progress.........: 62/62 (100.00%)
Rejected.........: 0/62 (0.00%)
Restore.Point....: 1/1 (100.00%)
Restore.Sub.#2...: Salt:0 Amplifier:0-62 Iteration:0-62
Candidate.Engine.: Device Generator
Candidates.#2....: s -> X
Hardware.Mon.SMC.: Fan0: 42%
Hardware.Mon.#2..: Temp: 46c
**snip**

34902903de8d4fee8e6afe868982f0dd:beef

**snip**

Started: Sun Mar 24 15:29:04 2024
Stopped: Sun Mar 24 15:29:13 2024

real	0m9.168s
user	0m1.211s
sys	0m0.576s

それくらい、単純に「ハッシュ化しただけ」では安心できないものなのです。

ハッシュしただけでは味気ないので塩を足そう

さて、ハッシュ関数や暗号関数を触っていくと「salt」という言葉が出てきます。一般的に「ソルト^🔈」と発音し、日本語で「塩」のことです。

コンピューターの世界で salt は、各々のデータに加えるランダムな数値や文字列のことを指します。先の例で言えば beef に加えた salt=1 です。

料理でいう「塩加減」のように「同じ具材でも塩の加減１つで味が変わるため、毎回調整が必要で加減も秘伝hidden」と言ったイメージが近いのですが、「塩土化」、つまり「戦時中の敵国が占領地の土地に塩を撒いて使えなくする」から来ている説もあるようです。

これまでの例のように、salt の値は「データの前」もしくは「データの後ろ」につなげてハッシュ化する方法によく使われます。

$a = hash( 'md5', $data . $salt); // 後から塩を足す
$b = hash( 'md5', $salt . $data); // 先に塩を足す

bashでの例

data='beef'
salt='1'

# 先に塩を足す（"1beef"）
hash_prepend_salt=$(echo -n "${salt}${data}" | openssl md5)
echo $hash_prepend_salt; # b14ab03be97e0b8deb2fa930cfdd4f4a

# 後から塩を足す（"beef1"）
hash_append_salt=$(echo -n "${data}${salt}" | openssl md5)
echo $hash_append_salt;  # 30017279d6a5bac241e764eeed261dd8

上記のように、salt を加えるとハッシュ値が変わるのは当然として、前後の salt を入れ替えるだけでもハッシュ結果が大きく異なります。

では、前に足すか、後ろに足すか、どちらのパターンが良いのでしょう。

塩は後から足そう

料理の場合、味を見て後から塩を足すのが基本であるように、単純に salt をデータに足す場合も、後から足すようにしましょう。

$a = hash( 'md5', $data . $salt); // 👍 ベター
$b = hash( 'md5', $salt . $data); // 👎 問題あり

これは、Length extension attack（「伸長攻撃」）と呼ばれるハッシュ値の衝突攻撃に弱いからです。

特に、MD5, SHA-1 や SHA-2 などの Merkle–Damgård と呼ばれる構造を使うハッシュ関数の場合についてまわります。発音は「マークル・ダンガード」のようです。ヒーロー・ロボットのような名前ですが、ブロック・チェーンに興味のある方は、この名前と salt を覚えておいてください。後から出てきます。

さて、この「伸長攻撃」攻撃を恐れずに短く説明すると以下の通りになると思います。

Y = hash( salt . X ) の X と Y がわかっている場合、salt の長さがわかれば salt が逆算できなくても Y = hash( salt . X . Z) の計算ができる。（. は文字列の結合子）

そのため Z に良しからぬ文字列を入れて Y の値を同じにすることができる可能性がある。

ソルトとハッシュ関数だけでパスワードをハッシュ化するのが微妙な理由 @ Qiita
Length Extension Attack ツール "Hash Extender" @ GitHub
- salt を secret、X を data、Y を signature、Z を append に置き換えて README をご覧ください。
- このツールの作者のブログに詳しい計算方法が載っています。
  Everything you need to know about hash length extension attacks @ SkullSecurity

逆に Y = hash( X . salt) と後に付け加える場合は、この攻撃を回避できます。「味付けは後から行う」（salt を加えるのは後）と覚えておきましょう。

塩だけでなく胡椒も足そう

この「salt」（塩）は基本的に個々のデータに加えるのですが、DB の場合、全体に加える「pepper」（胡椒）と呼ばれる値もあります。

ソルト（暗号化）@ Wikipedia 日本語
ペッパー（暗号化）@ Wikipedia 英語

例えば、下記はプレーンな（加工や手を加えていない素すの状態の）パスワード情報です。偶然にも user1 と user2 のパスワードが同じです。

ユーザ名	パスワード
user1	`passw0rdA`
user2	`passw0rdA`

上記だと流出時にバレバレなので、次のようにパスワードに塩・胡椒して味付けします。

passwdとsaltとpepperの文字列変数をつなげてMD5でハッシュ化する例

$passwd_hashed = md5($passwd . $salt . $pepper);

ここでは可読性のために脆弱な MD5 を使いますが、パスワード保存に MD5 が使われることはありません。

DB の保存で考えると、定数に pepper='pepperA' と設定しておき、テーブルは以下のようなイメージになります。

ユーザ名	パスワード
user1	`7915e17989dcbb1d2132c1d207ef9e1d`
user2	`5ee508cb664f91000826933e626cd5df`

ユーザ名	ソルト
user1	`saltA`
user2	`saltB`

DB ファイル自体が流出したらテーブルをわけても同じことであるため、パスワードとソルトを同じテーブルに格納する場合もあります。どこに格納するかは運用の考え方しだいだと思います。

「ならば、ソルト値を別 DB に保存してリスク分散しなきゃ」と言った、沼にハマったのであれば、以下の記事を一読することをオススメします。

ソルト付きハッシュのソルトはどこに保存するのが一般的か @ Qiita

さて、全体に胡椒を加えるpepper値を使うメリットは、DB のファイルが流出した場合の迅速な対応が取れることと、全体のコントロールを取りやすいことです。

pepper の定数が流出していなければ、流出した DB の salt 値からだけでは保存されたハッシュ値を算出するのは大変なので、2 つ目のブロック防壁としては機能します。しかし、攻撃者が予めダミーのアカウントでパスワードを登録しておけば、パスワードと salt 値はわかることになるので、pepper 値の算出は時間の問題となります。

このような事態の場合、まずは「ユーザー全員にパスワードを再設定をしてもらうこと」が最優先です。そこで、pepper 値を変えれば、すべての保存値と計算が合わなくなるので全体をロックできます。

この胡椒を効かせる方法は、アイデア次第で色々と使えます

ログイン時の cookie の ID などでも使われるテクニックで、不審なログインを複数ユーザーで検知した場合に、pepper 値を変えることで、全員を強制的に再ログインさせることができます。

他にも、定期的に pepper 値を変えて、その後「更新した・しない」でアクティブ・ユーザーを確認したり、アプリに興味のないユーザーをふるい・・・にかけたりするのにも利用できます。スマホのアプリでも定期的に再ログインさせられ、舌打ちしたことがあると思いますが、アレです。

もちろん、スマホの OS のアップデートやセッションの期限切れによるものもありますが、「更新」という名において、いささかダークなパターンにも利用される可能性があるということです。

また、実際に salt や pepper 値を使う場合は以下のように、より複雑にシェイクします。

"saltA" などの単純な文字列でなくランダムな数値や文字列を使う
アルゴリズムを sha256 や sha512 などのより複雑なアルゴリズムを使う
hash('sha256', hash('sha256', $value)) と二重・三重にハッシュ化させたりする（時に数万回）

🐒 3 番目のループですが「Key stretching」（ストレッチング）と呼ばれる「総当たり攻撃対策」の 1 つです。

一言で説明すると「1 回の処理に手間をかけさせる対策」です。

主にローカル（流出先）での「総当たり攻撃」の対策で、1 回ハッシュ値を算出するのに手間をかけさせることで、最終値を見つけるまでの時間を伸ばす（ストレッチする）と言う手法です。

例えば、平均して 1 秒かかるくらいに何度も（時に数万回も）ハッシュ関数に通した最終的なハッシュ値を保存して使います。

これにより、1 回のログインに 1 秒かかるものの、総当たり攻撃時には 1 秒に 1 つしか確認できないということでもあります。これにより、攻撃の回数を劇的に減らせます。

他にも、サーバ側で行うストレッチングに「遅延」があります。

例えば、リクエストを受けてハッシュ値を確認する際のタイミングに、わざと sleep を入れて遅延させ、「リトライ回数の制限」と組み合わせることで 1 回の攻撃に手間をかけさせることで総当たり攻撃をし辛くさせます。

ログインなどで、成功するとサクッと入れるのに、間違えると「DB を総なめしてるのかな？」的に反応が遅くなるのを感じたことがあると思いますが、アレがストレッチングです。

この「ストレッチング」は、後述するブロック・チェーンにも「nonce 探索」として活用されています。

パスワード・ハッシュとは

さて、ここまではパスワードの保存に関する話がメインでした。

しかし、本記事はセキュリティのための記事ではありません。あくまでもハッシュ関数の基礎知識と「活用」に関する記事です（「結構、セキュリティ（暗号）の話しをしとるやないかい」と思うかもしれませんが、我々の世界でいう「HDD と SSD の説明と違い」を説明している程度の内容らしいです）。

「安全なパスワード保存」にハッシュ値を使いたいのであれば、パスワード管理専用の関数やフレームワークが各々のプログラム言語には数多くあります。一般的にハッシュ値をパスワード管理に特化したものを「パスワード・ハッシュ」と呼びます。

自分で実装するよりは、それらを利用した方が楽らくだし、何より安全です。例えば PHP の場合であれば password_hash() という、まんま・・・の関数があります。

先の「ストレッチング」のように「パスワード・ハッシュ」は計算のしづらさ（面倒くささ）に重点をおいているので、速度の速さと強度が重視される「ハッシュ関数」とは目的が違います。

2021/03/01 現在、最強のパスワード・ハッシュは Argon2 と思われます。2013 年から 2015 年にかけて行われた PCH というパスワード・ハッシュの競技会で優勝したのが Argon2 だからです。

Argon2 には、Argon2i と Argon2d の大きく 2 つあります。

Argon2i は、処理時間やハードの電圧など物理的に観察して情報を盗むサイドチャンネル攻撃に耐性があり、Argon2d は、GPU 攻撃（単純な計算の並列処理）に強い耐性があるアルゴリズムです。そして、両方を備えたアルゴリズムが Argon2id です。

例えば PHP 7.3 以降では両方に対応した PASSWORD_ARGON2ID が使えます。（オンラインで動作をみる @ paiza.IO）

また、Go の場合は golang.org/x/crypto/argon2 の公式パッケージが使えます。いささか使いづらいので、手前味噌ですが、使いやすくしたパッケージ "go-argonize" も用意しました。どのように使うのかの参考にしてみてください。

セキュリティの記事ではないとは言え、セキュリティが心配でハッシュ関数を勉強に来たという方は、かの Web セキュリティのバイブルとも言える「徳丸本」で有名な徳丸先生の Youtube 動画チャンネルを入り口とする（フォローする）ことをお勧めいたします。その上でバイブルの１冊くらいは持っておくと良いと思います。

ぶっちゃけ、こんなジャンクで基本的な内容の記事を読むより、先生の本や e ラーニングのコースを受講された方が実装の役に立ちます。

徳丸浩のウェブセキュリティ講座 @ Youtube
先生の e-ラーニングサービス @ Security Campus [説明動画]
徳丸本「体系的に学ぶ安全なWebアプリケーションの作り方第2版」
〜脆弱性が生まれる原理と対策の実践〜
- ISBN-10: 4797393165
- https://amazon.co.jp/dp/4797393165/ @ Amazon
- ここ 1 年の「徳丸本」に関する Qiita 記事 @ Google

これから使うなら SHA-3

パスワード以外のデータのハッシュ化に強いアルゴリズムが欲しいと悩んだら、とりあえずは「SHA3-512」を選ぶといいでしょう。次点で、SHA3-256 でしょう。OS やプログラム言語間で互換性が高い（汎用度が高い）中では、一番強いハッシュ・アルゴリズムだからです。（2020/10 現在）

ぶっちゃけ SHA-2 の SHA-256 や SHA-512 でも実用としては現状十分です。

しかし、SHA-2 は 20 年以上前のアルゴリズムであること、脆弱性（合理的な衝突方法）が発見されている SHA-1 の親戚であること、今後の演算力の向上により SHA-2 も時間の問題であることから、移行が推奨されていることを知る必要があります。

これから実装するのであれば SHA-1 や SHA-2 とはまったく違う概念のアルゴリズムで SHA-2 の後継と正式に制定された SHA-3 の利用を検討する価値はあると思います。

ここまでに SHA-1、SHA-2、SHA-3 といった「SHA なんとか」が、ちょいちょい出てきました。SHA（シャー）は "Secure Hash Algorithm" の略で NIST が作成・制定・推奨するハッシュ・アルゴリズム全般を指します。
例えば SHA-2 は SHA-224、SHA-256、SHA-384、SHA-512 の総称で、各々ハッシュ値の長さ（ビット長）のバリエーションを表しており、Merkle–Damgård 構造をベースに作成されたものです。
同様に SHA-3 も、ビット長ごとにバリエーション（SHA3-256 など）があり、 Keccak アルゴリズムをベースに作成されたものの総称です。SHA-3 には、任意の長さのハッシュ値を得られる SHAKE128 と SHAKE256 があり、128 や 256 はハッシュ値の長さではなく、その内部強度を表しています。
ちなみに NIST は、米国の国内標準規格の制定団体のことです。世界標準規格の ISO（そのうち日本語に訳され適用したものが JIS）が「製品やサービスの品質や安全性の向上を図るための規格」であるのに対し、NIST の規格は（冷戦時代に重要視された）「セキュリティと国土安全保障」が、より強く意識されています。
そのため、以前までは米国政府の安全保障局（NSA）が作成したアルゴリズムを制定していました。しかし、近年は「世界中の暗号学の研究者から安全性を高く評価された暗号技術」が選定されるようになったため、NIST 制定の暗号アルゴリズムやハッシュ・アルゴリズムは、インターネットの事実上の標準（デファクト・スタンダード）として使われています。つまり、RSA、AES、SHA といった NIST 制定のアルゴリズムは誰でも知ってるし、使えるという状況であるということです。

とは言え、強いアルゴリズムほど複雑さが増すため処理速度やレスポンスの問題も出て来ます。

どの程度複雑化させるのかも運用の考え方しだいになると思います。一旦強いもので組んでから、予算・運用コスト（計算コスト）・UX と相談しながら、測定しながら低い方へ検討してください。（「憶測するな、測定せよ」です）

いずれにしても、引数に $salt や $pepper およびハッシュ化のループ回数という、絶対公開しない要素加えることで予測を難しくさせているのです。

もちろん salt 値や pepper 値が流出してしまうと意味がありません。シオシオのパーです。つまり、秘密鍵と同じくらい扱いには気をつけないといけないので、「ハッシュ化しても安心できない」とわかると思います。

塩に工夫をして秘密の共通レシピを作ろう（簡易共通鍵の作り方）

さて、元のデータに秘伝hiddenの salt 値を加えてハッシュ化することで、元のデータのハッシュ値を隠蔽いんぺいすることができました。

ここで、salt 値を「外部に公開してはいけない値」なおかつ「元の値を引き出す・特定するために使われる値」とすると、salt は秘密鍵keyと同じ定義を持つことにお気づきでしょうか。

この salt 値を使った仕組みをさらに工夫すると、2 者間でお互いの秘伝hiddenの salt 値から共通の salt 値を作成することができます。

つまり、俗に言う「共通鍵」のようなものが、お互いの秘密鍵salt値から作成することができるのです（鋭い人はお気づきかもしれませんが、そうです「ディフィー・ヘルマン鍵共有」のことです）。

注意点として、このような使い方の値を salt とは呼びません。ここでのポイントは「お互いの秘伝hiddenの値を相手に知らせなくても、加え方次第で共通の鍵が作成できる」という点です（ゆうて、足し算的なことをしているだけなのですが）。

さて、基本的な仕組みですが、数式を使うと頭がチャンポンしちゃうので「色をチャンポンする」と例えると理解しやすかったです。

と言うのも、データに salt 値を加えてハッシュ関数でゴチャ混ぜにするというのは、別の見方をすると「とある色」に「俺様カラー」の絵具を混ぜるようなものとも言えます。

そこで「共通鍵の作り方の流れ」を、まずは色を使った概念図で全体を把握したいと思います。

下図における「共通色」は Alice と Bob が事前に合意している色、「秘密色」は各々がランダムに選んだ色、と考えながら下の図を見てください。

ここでのポイントは「秘密色の交換をしていない」ことと、「色を混ぜているだけ」です。


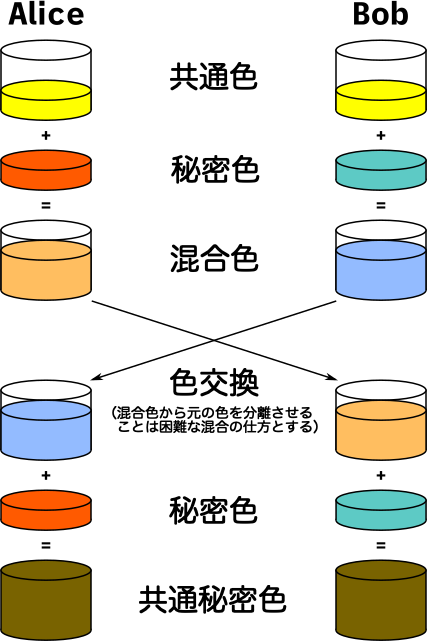_{^{"Diffie–Hellman key exchange" @ 「ディフィー・ヘルマン鍵共有」の英語版 Wikipedia より筆者による日本語訳}}

色で概念を捉えたとは言え、コードで書かないと理解できないタイプなので、上記を Bash で再現してみました。

いささか分かりづらいですが、"yellow" "red" "green" の文字列を MD5 で数値化し、上記の図の通り足し算しているだけです。Alice.sh と Bob.sh がお互いの秘密色（xxxSecretColor）を参照（受け取って）いないことに注目してみてください。

オンラインで動作を見る @ paiza.IO

鋭い人は「えー。でもお互いに同じ『共通色』を持っているんだから、『相手から受け取った混合色 - 共通色』と引き算すれば相手の秘密色がわかっちゃうじゃん」と気づくでしょう。

かく言う私は、自分で bash で実装してみて初めて気づきました。足し算でなく掛け算であっても同じです。割っちゃえばいいので。

上記図にある色交換のコメントで「混合色から元の色を分離させることは困難な混合の仕方とする」とあります。

つまり、2 つの値をゴニョゴニョと混ぜて 1 つの値を出すことを「色を混ぜる」と表現しているのですが、単純な足し算や足し算の連続（掛け算）は「分離させることが簡単な混合の仕方」ということになります。

では、色交換した値を自分の秘密色で hash(<色交換した相手の色> + <自分の秘密色>) のようにハッシュすれば良いかというとダメで、塩を前に足すか・後に足すかで大きく変わってしまうからです。

そこで再登場するのが割り算の余り。そう、mod（剰余、%）です。

X は、A と B を掛けて Y で割った時の余り

X := (A * B) % Y // X から見ると、Y は予測できても、A と B の組み合わせは謎

つまり「割り算の余りからは、元の組み合わせを得ることは困難」という性質を使って「元の色（値）の組み合わせに分離させることは困難」という状況を作ります。そして B を秘密色、A と Y の 2 つを共通色とするのです。

ここで、アホみたいな話しですが「a * b は b * a と同じ結果になる」という算数を思い出してください。

そして、同様に下記の 2 つは同じ結果になります。

(a³)² = (a * a * a) * (a * a * a) = a^3*2 = a⁶
(a²)³ = (a * a) * (a * a) * (a * a) = a^2*3 = a⁶

これは数学的に表現すると (a^x)^y = (a^y)^x = a^xy, x = 3, y = 2 と表せます。落ち着いて見比べれば何てことないことを、短く表現しているだけです。

さて、この a^x と a^y を上記の色の概念図で交換される混合色とした場合、a が共通色、x と y が各々の秘密色とできそうです。

すると、各々算出する「共通秘密色」（共通の値 a^xy）は (a^x)^y と (a^y)^x と計算できそうです。

しかし、これでは（ただの掛け算なので）余りよろしくありません。

そこで両辺を同じ値 p で割った余りを出してみます。以下の 4つは同じ値になるのがおわかりでしょうか。

(a^x)^y % p
(a^y)^x % p
a^xy % p
a^yx % p

これで「共通秘密色」が流出しても、a^x もしくは a^y の算出は難しくなります。

つまり、a とペアになる値 p を用意し、この 2 つの値をセットで「共通色」（事前に合意している色）とできそうです。

この考え方、つまり「掛け算の順番を変えても同じ値になる」「掛け算の結果が同じなら、それをさらに同じ値で割っても余りは同じになる」が、共通の秘密鍵を作成する際の基本となります。

とは言え、上記で問題なのが「お互いが a と p を知っていること」です。

交換しあった混合色（a^x もしくは a^y）から相手の秘密色の値（x と y）は算出できてしまいます。受け取った混合色を、結果が 1 になるまで a で割った回数が相手の秘密色だからです。

なんか、振り出しに戻ってきてしまいました。

そこで、相手に渡す混合色を p で割った余りにしたらどうでしょう。

旧混合色 % p = 新混合色
- a^x % p = X
- a^y % p = Y

これであれば、お互いが a と p を知っていても X や Y からは、秘密にしている x と y の色（値）の算出は劇的に難しくなります。

つまり、受け取った新しい混合色を各々は以下のように計算して、共通秘密色を算出することになります。

色交換後の共通秘密色の算出（新バージョン）
- (Y)^x % p = (a^y % p)^x % p = 共通秘密色
- (X)^y % p = (a^x % p)^y % p = 共通秘密色

果たして「割った余りを、さらに割った余り」が同じ値になるのでしょうか。

それでは、以上を踏まえて Alice と Bob の公開鍵を改めて作ってみましょう。今度は、足し算ではなく割り算の余り、つまり mod（剰余）を使ってみます。

まずは、Alice と Bob は秘密鍵として、各々ランダムな値を決めます。ここでは、わかりやすいように Alice の秘密鍵を a、Bob の秘密鍵を b とします。

a = 4 // Alice の秘密鍵（ランダムな値）
b = 3 // Bob の秘密鍵（ランダムな値）

次に、事前に合意している 2 つの値（共通色）として、g と p の値を決めます。変数なので、x と y にしてもいいのですが、気分です。なんか、みんなこの変数名を使いたがるので。

// 事前に合意した値（セットで共通色とする）
g = 5
p = 23

g と p の値ですが、本来はバカでかい素数を元に作られるのですが、わかりやすくするために 5 と 23 にします。

ちなみに、g は generator の略で乱数関数で言うところの seed 値的な役割をする値で素数です。p は prime（素数）の略です。ここでは「事前に合意している 2 つの定数 g と p がある。どうやら素数らしい」程度に考えておいてください。

それでは、まずは Alice の公開鍵（混合色、pubA）を作ってみましょう。

事前に合意している g と p を元に、自身の秘密鍵（a）を使って計算するのですが、計算方法は以下の通りです。g を a 回掛けて、p で割った余りを公開鍵としているだけです。

pubA = (g)^a % p

同様に、Bob も公開鍵（混合色、pubB）を秘密鍵（b）を使って計算します。

pubB = (g)^b % p

次に、各々が公開鍵を交換（相手の公開鍵を参照）して、秘密の共通鍵の計算をします（commonA と commonB）。計算式は以下の通り。

Alice の計算
- commonA = (pubB)^a % p
Bob の計算
- commonB = (pubA)^b % p

共通鍵の計算といっても、秘密鍵を作った際の g を相手の公開鍵と入れ替えただけです。見比べてみてください。

それでは、実際に代入して（a = 4, b = 3, g = 5, p = 23 で）計算してみましょう。すると、共通の秘密鍵は同じ値になります。

公開鍵（混合色）の計算
- pubA = (g)^a % p = 5⁴ mod 23 = 4 ... Alice の公開鍵
- pubB = (g)^b % p = 5³ mod 23 = 10 ... Bob の公開鍵
共通秘密鍵の計算
- commonA = (pubB)^a % p = 10⁴ mod 23 = 18 ... Alice の共通秘密鍵
- commonB = (pubA)^b % p = 4³ mod 23 = 18 ... Bob の共通秘密鍵

なんと、割り算の余り（公開鍵）を、さらに割り算すると、余り（共通鍵）が同じになりました。（オンラインで動作を見る @ paiza.IO）

なぜ同じになるのかというと、剰余（modulo）には面白い性質があって、g と p が素数の場合、ある条件下において (g^a % p)^b % p は g^ab % p と同じになる性質があります。

(g^a mod p)^b mod p = g^ab mod p

試しに (5⁴ mod 23)³ mod 23 と 5^(4*3) mod 23 が同じ答えになるか試してみてください。

これは y = x mod p の場合、つまり x を p で割った余りの y は 0〜(p-1) の間を循環するという剰余の性質と、1 と自分自身以外では割り切れない素数の性質を利用していて、ぐるりと巡りに巡って同じになるような感じです。

ここで注目して欲しいのは、上記の証明や条件の詳細ではなく、以下の点です。

公開鍵は g^a mod p と、余りを使っているため a を特定することは難しい。
p と g が素数の場合、ある条件下において以下が成り立つ。
- (g^a mod p)^b mod p という計算は、g^ab mod p の計算と同じ結果になる。
- (g^b mod p)^a mod p という計算は、g^ba mod p の計算と同じ結果になる。
- g^ab mod p は、g^ba mod p と同じこと。

以上を踏まえて、改めて図を見てください。混合色を「割り算の余り」を使うことで、色を分離できない状態にしているのが面白いと感じませんか？


_{^{"Diffie–Hellman key exchange" @ 「ディフィー・ヘルマン鍵共有」の英語版 Wikipedia より筆者による日本語訳}}

この、混合色を交換して共通の秘密色を生成する概念を「ディフィー・ヘルマン鍵共有」（DH）と言います。

色交換に使われる混合色の作成は、今回のような mod を使ったもの以外にも、方程式（曲線）を使ったもの（ECDH）などがあります。

ECDH の基本概念をザクっと説明すると、事前に共通色となる方程式を決めておき、秘密鍵と公開鍵を方程式に掛け算した座標を交換しあうことで、お互いの線が交差する点を共通秘密鍵の値とするものです。

先の MOD（余剰、%）を使った方法のポイントは、割り算の余りを使い「組み合わせを無限にした」ことで、色交換する際の混合色、つまり「元の組み合わせに分解できない状態」にしたことです。

そこで、2 つの点があれば直線が引けることを思い出してください。そこから、導き出された方程式（ｙ＝ａｘ＋ｂ）を相手に渡しても、最初の 2 つの点は相手にはわかりません。

また、2 つの点のうち 1 つを共有しても、その方程式（もしくは傾き）からは 2 つ目の点はわからないため、受け取った相手は元の組み合わせはわからない（混合色から共通色と秘密色には分解できない）という状況が作れます。

そして、お互いが交換した方程式（or 傾き）が交差する点を共通点（共通秘密色）とすることができます。

このような考え方を、直線ではなく楕円曲線（EC、Elliptic Curve）を使ったものが ECDH です。

以下は Go 言語ですが、オンラインで動作が見れます。

オンラインで Go の ECDH による秘密鍵共有の動作を見る @ GoPlayground
- 参考文献：【Golang】ECDH 公開鍵から DH 鍵交換で共通鍵を作成する（ディフィー・ヘルマン鍵共有） @ Wiita

「（え？使うには、こんなもんでいいの？）」と思えればシメたものです。複雑な仕組みをリスペクトした上で関数化して利用する（盲目的に関数を使っていないという）大事な使い方が見えた証拠だと、私は思います。

ここでのポイントは「一方向への算出は簡単だが、逆方向は難しい」（ここでは色分解）という考え方が、暗号（セキュリティ）には重要であるという具体例です。

ストーカー・チャーリーの中間者攻撃

mod を使った DH、楕円曲線を使った ECDH、どちらも「とある問題」を除けば、堅牢な秘密の共通鍵が作成できる方法です。

そして、とある問題とは「中間者攻撃」です。

計算方法自体は堅牢なものの、実は、これだけではセキュリティー上よろしくありません。お気づきでしょうか。色交換で受け取った相手の混合色の「配合」は、お互いがわからないことに。

アリスAliceとボブBobが色交換をする際、中間にチャーリーCharlieがコッソリ入っていた場合、意図せずダミーの共通秘密色を使わせることができてしまいます。

つまり、色交換している相手が実はチャーリーだった場合です。チャーリーが適当な色を作って両者に渡してしまえば、両者は気付かないうちにチャーリーとの「共通秘密色」を作成していることになるのです。

これは、例えば github.com にアクセスしているのに、ダミーの IP アドレスにアクセスさせることで実現可能です。hosts ファイルの一時的な書き換えや、ダミーの DNS サーバーを立てて、DHCP をいじるなどです。

このように、中間にチャーリー的なストーカーが居た場合の攻撃に弱いということです。https 接続が重要という理由の 1 つがここにあります。

https 接続以外にも追加対策として、アリスとボブが「オンライン以外で、事前にランダムな数値を共有しておく」という方法があります。そして、そのランダム値を salt 的に使います。つまり、生成した共通秘密鍵を直接使わず、共通の salt を加えてハッシュ関数を通したものを最終的な共通秘密鍵とするなどです。

これにより、中間者を通すと自分以外は誰も復号できない状態になるので、異常を検知する手助けになります。TOTP といった、2 要素・・認証が重視される理由も見えてくるのではないでしょうか。

手前味噌ですが、Go 言語で手軽に TOTP を実装するパッケージに、ECDH 鍵交換機能を付けたものをリリースしています。

https://github.com/KEINOS/go-totp @ GitHub

これは、ECDH 鍵交換で生成された共通秘密鍵を TOTP の秘密鍵に利用して、Alice と Bob が同じパスコード（有効期限のある n 桁の数値）を発行できるものです。このパスコードを SALT 値として利用します。かなりニッチな機能ですが。

このような、秘密鍵や共通秘密鍵を直接使わず、一旦それらをハッシュ関数に通したものを使ったり、salt 値を加えるという手法は、そこかしこで使われます。

そして、salt の概念をベースにしているものの、用途が異なる場合、各々に名前が付いていたりします。

例えば MAC（Message Authentication Code）などです。「塩を加える」という概念を持つと、読んでいて「あー。なるほど」と思えることが多いです。

ところが、せっかく塩・胡椒をして独自の味付けをしたのに「同じ味や歯ごたえなのに実は合成肉だった」みたいな、なりすましが発生するご時世になってきました。

詳しくは後述の「MD5 と SHA-1 のセキュリティについて」でも説明しますが、塩・胡椒しただけの粗挽き肉ではグルメセキュリティ重視の人を唸らせることは難しくなってきているのです。

データの「指紋」としてハッシュ値を使う

ハッシュ関数はセキュリティ用途ばかりがクローズアップされますが、「処理」に目を向けると「数値で返ってくる」という特徴はデータの管理に活かすことができます。

ハッシュ値の王道の使い方は「変更の検知」です。１バイトどころか１ビットでも違いがあるとハッシュ値の結果は大きく変化します。この特徴により、大量の文書（データ）であっても１文字の変化を検知できるのです。（変化した場所の特定は別の話し）

この「本編を詳細に見なくてもザッと見るだけで把握できる」的な意味で「ハッシュ値」を「ダイジェスト値」もしくは「メッセージ・ダイジェスト」と呼ぶこともあります。また「ハッシュ関数」は「要約関数」とも呼ばれますが、個人的に「『要するに...』と言われても、まったく意味がわからないのと似た関数」だと思っています。

むしろ、海外ドラマなどの冒頭で流れる「前回までのなんとか」のダイジェストのように「以前が何であったか、わかっている人にしか伝わらない確認をするためのもの」といったイメージです。

^{🐒 「ハッシュ値」「メッセージ・ダイジェスト」どちらも同じものですが、暗号関連などの確認に使う場合に「ダイジェスト値」と呼ぶことが多い気がします。この記事では「ハッシュ関数」の値という意味で「ハッシュ値」と統一します。}

「データに変更がないか」の、最も一般的なハッシュ値の活用方法は、おそらくダウンロード・ファイルの確認でしょう。

ZIP や ISO といった巨大なアーカイブ・ファイル（複数ファイルを１つにまとめたファイル）をダウンロードする際に、リンクと一緒にファイルのハッシュ値が添えてある、アレです。ダウンロードしたファイルのハッシュ値と比べることで、破損もしくは改ざんされていないことが確認できます。

逆に言えば、「ハッシュ値が同じであれば、データに変更はない」という使い方でデータの管理にも利用できます。

みんな大好き git などは、ファイルの diff のハッシュ値を比較して変更があったかを検知しています。アプリやライブラリなどの管理で、いつもお世話になっているパッケージマネージャーも、競合や改ざんを防ぎつつ共通の動作をさせるために ライブラリ名<ハッシュ値> のような形式で内部管理していたりします。

他にも、BitTorrent（P2P 型ファイル転送システム）や後述する IPFS（P2P 型分散ファイルシステム）などは、ネットワーク上に「名前は異なるが、実は中身は同じ」ファイルがあってもファイルのハッシュ値を使うことで同等に扱えるようになっています。

身近なところでは、Web サーバーなどに画像やファイルがアップロードされた際、既に同じものがあるかをファイルのハッシュ値で確認をしたりもできます。

これを応用して「微妙に異なるが、ほぼ似たようなデータ」が多いものなどは、ストレージ（データの保存先）の容量を節約することもできます。

例えば保存したいデータを n バイトごとに分割して、分割された状態で保存します。次に、分割されたデータのハッシュ値を算出し、バイナリ・ツリー（1 つの親に対し 2 つの子を持つ）構造で各々ハッシュ値を算出して、ファイル全体のハッシュ値を出します。最後に、それらの値を DB などで管理します。


ハッシュ木 @ Wikipeida より

これにより、類似データを保存する際に、既存の共通する分割データは保存せず、異なるデータだけを保存すれば容量を節約できるという考え方です。後述する IPFS は、この仕組みをデータの取得にも応用したものです。余談ですが、MD5 や SHA2 といったハッシュアルゴリズムも、この考え方をベースにしています。

このように「ファイル名が異なっていても、中身が同じファイルであった場合はハッシュ値は同じ」ということを、逆手に利用したデータの管理方法に使えます。

そのため、ファイルの中身を特定する目的で作成されたハッシュ値を「フィンガー・プリント」（指紋）と呼ぶこともあります。

ハッシュ関数がセキュリティ目的が多いのは、指紋と同じで「識別 ID として使えるから」なのです。

するどい人は「え？じゃあ、電帳法とかの、電子取引データを保存する際の訂正・削除・改竄かいざん防止対策にもハッシュ値って使えるんじゃねーの？」とお気づきでしょう。

預言者の予言を担保する（当たるとは言ってない）

さて、この「ハッシュ値が同じならデータに変更はない」仕組みをさらに工夫すると、「俺様」電子証明書が作れます。「電子署名」でなく「電子証明書」です。

どういう事かと言うと、「ハッシュ値」と「公開鍵・秘密鍵暗号」を組み合わせることで簡易的な電子証明書が作成できるのです。

つまり「内容が同じものである」ことを証明できるのです。（内容が信用できるとは言ってない）

具体的に言うと、ファイルのハッシュ値を自分の「秘密」鍵で暗号化して公開すれば、それが俺様電子証明書になるのです。

まずは暗号化にも使う公開鍵と秘密鍵を使った、なんちゃって証明書の作成方法です。

自分が正しいと認めたファイルのハッシュ値を自分の「秘密鍵」で暗号化し、それを「証明書」としてファイルと一緒に公開し（相手に渡し）ます。
相手は、そのペアとなる「公開鍵」で証明書を復号して対象のファイルのハッシュ値と比較します。
同じハッシュ値であれば、相手は「自分が認めたファイルである」ことが確認できます。

これは公開鍵・秘密鍵の「片方の鍵で暗号化したものは、もう片方の鍵でしか復号できない」という特徴を活かした手法です。

ここで「別にハッシュ値じゃなくてもファイル自体を秘密鍵で暗号化すれば、（復号できたら）それ自体が証明になるじゃないか」とお気づきかもしれません。

鋭い。

確かに、なんちゃって証明書では「アーカイブのハッシュ値の計算」→「証明書の復号」→「ハッシュ値の比較」と、いささか手間がかかります。

公開鍵で復号できたら一発で確認できるのですが、問題は「暗号化」です。

というのも、復号の処理はハッシュ値の処理より負荷（時間）がかかります。しかも、ファイル・サイズが無駄に大きくなります。ギガ単位の大きなファイルの場合は、特に顕著です。

「誰がアクセスしてもいいけど、自分の提供したファイルだとユーザーが確認できるようにしておきたい」場合の方が多いため、一般公開データを暗号化して提供することは（あることはありますが）少ないです。

とは言え、ハッシュ値を使うにしても、証明書の確認に 3 ステップかかるのは手間ではあります。

... ... どうしよう。

そこで出てくるのが、両方のいい所どりをした「電子署名」です。

つまり、「ファイル」と「秘密鍵」をハッシュ関数に通してゴニョゴニョしたものを「署名」とするのです。

そして確認側は、「ファイル」と「公開鍵」と「署名」のデータからハッシュ値を算出し、同じであれば「署名」は有効と判断するのです。

ここでのポイントは「秘密鍵もハッシュ値も署名も数値である」ことと、「署名に必要な公開鍵、秘密鍵はランダムな数値でも構わない」ということです。

もう少しザクっと説明すると、「電子署名」は秘密鍵から作成した署名鍵と、Siglet と呼ばれる小さなデータをセットとした 64 バイトのデータです。Siglet とは、ハッシュ値・秘密鍵＋署名鍵で算出された値です。使われるハッシュ値は、署名鍵の一部とファイルをハッシュ関数に通したものです。

確認側は、ファイルと署名鍵をハッシュ関数に通し、ハッシュ値・公開鍵＋署名鍵 で Siglet 値と同じか検証することで確認します。

暗号化・復号を使わずともハッシュ値を出すだけでよく、計算量も少なく速いので、現在はこの手法がメジャーです。この手法をシュノア署名と言います。

ここで重要なのが「署名」という単語の再認識です。

「署名」は英語で言うと「sign」です。日常では「社長、ここにサイン捺印ください」という、アレです。

社長がサイン捺印することで、「社長が認めた書類」という意味を持ちます。そして、社長のハンコが誰でも使えたり、押せたりすると意味がありません。そのため、社長印や会社印は金庫にしまってあると思います。

しかし、重要なのはハンコではなく「その人が認めたものである」と証明できることです。そのため、手書きのサインでもいいし、拇印でもいいわけです。

電子署名も同じです。「その人が認めたものである」と証明できれば、何だっていいのです。

確かに、電子署名に使うハンコ（鍵）は大事にしないといけないので「秘密鍵」という言い方をします。しかし、だからと言って「秘密鍵で電子署名する」というのは暗号化するというわけではありません。

くどいですが、「秘密鍵Key」というのは、value（価値）を引き出すのに必要な非公開の値です。そのため、暗号化用の秘密鍵でなくても、ランダムな数値でも構わないのです。

公開鍵・秘密鍵による署名では RSA 鍵を使った署名が有名ですが、これは「たまたま」暗号用の鍵が署名に使えたというだけで、「署名は RSA 鍵で行うもの」というわけではありません。

最近では git などでも移行が進んでいる、シュノア署名の 1 つの Ed25519 が主流になりつつあるようです。（RSA と Ed25519 の強度の違いは、後述する IPFS で軽く説明します）

閑話休題。

さて、検証や証明にハッシュ値を使うメリットはデータサイズを小さくできるだけに過ぎません。

秘密の鍵をベースに作成され、不特定多数が公開された鍵で確実に確認できれば、何だって署名（サイン）となります。別に鍵が暗号化用の鍵でなくたっていいのです。

あとはプロトコル双方の合意の問題です。

どのような方法にせよ、電子証明は「本物同一のものであることが証明できればいい」ので様々な手法があります。

署名の例として、GitHub などのリポジトリや、OS などのリリースページで、リリースされたファイルと共に *.sha256 *.sha256.sig といったファイルがあったりしますが、それらです。

*.sig 以外の拡張子もあります。しかし、いずれもファイルのハッシュ値を羅列したリストと、そのリストを署名したファイル（*.sig や *.gpg など）のセットが大半です。

大容量のファイルを担保するために、ハッシュ値のリストと、それを署名した例 | 22.04 @ Ubuntu リリースページ

署名ファイルがある場合は、リポジトリ・オーナーが「対象のファイルが正式なものであるとサイン（署名、signサイン）した」という意味で、*.sig ファイルが捺印のような役割を持ちます。そして、捺印と判子を透かして照会する役割をするのがリポジトリ・オーナーの公開鍵です。

ここで復習ですが、重要なのが署名ファイルは安全性を証明するものではないということです。

あくまでも代表者や著者自身が「認めたものである」というサインをしたものなのです。そのため、サイン（*.sig）があっても、盲判、俗に言う「めくら印」である可能性もあるため、必ずしも「安全である」とは言えないことを念頭に置きましょう。

それでもサイン（署名ファイル）が「ある」「なし」では、あった方が安心感が違います。同じ書類でも社長印が押されたものと、そうでないもののような違いです。

マスター、うんちくはいいから早く食えるものをくれ

以下が具体的な署名（サイン）の仕方と検証の例です。

*.sha256 が各ファイルの（SHA2の 256,SHA256 による）ハッシュ値一覧で *.sha256.sig がその署名ファイルです。

$ # ハッシュ値の算出
$ openssl dgst -sha256 sample.txt >sample.hash

$ # 「秘密」鍵で署名（sign, signature）
$ openssl rsautl -sign -inkey privatekey.pem -keyform PEM -in sample.hash >sample.sig

$ # 「公開」鍵で検証（verify）
$ openssl rsautl -verify -inkey publickey.pem -pubin -keyform PEM -in sample.sig

いずれの方法でも、このような、「秘密鍵・公開鍵のペア鍵の作成」「証明書の作成」「復号および検証」といった一連の仕組みを総合して「デジタル署名」と呼びます。証明書の作成は、これらの応用でしかありません。

デジタル署名の面白い使い方としては「予言の書」などがあります。

事前に予言と予言した日付を書いておき、「秘密」鍵で暗号化したその予言（ファイル）と、その電子証明書を同時に公開します。そして予言後に「公開」鍵を公開するなどです。まぁ、予言なので普通に公開しちゃっても良いんですけど。

上記コマンドのように、ファイルをデジタル署名することは難しいものではありません。

ファイルを秘密鍵（非公開値）で署名して、公開鍵（公開値）を公式な場所に公開すれば、何にでも「公式なもの」として示せます。

後述する NFT でも述べますが、デジタル作品の作家の方には、自身を守るためにも鍵の作成と署名の仕方は、ぜひ覚えてもらいたい仕組みです。

肥大化しないパターン ID

「引数がどれだけ長くても、ハッシュ値は固定長の数値」であることもメリットです。つまり、データがそれ以上増えないということです。

例えば、Web サイトのページ遷移せんいのパターンを固定長の ID にすることもできます。

ページせん移をID化する

$list_url_visited=[
  'http://hoge.com/p1',
  'http://hoge.com/p6',
  'http://hoge.com/p4',
  ...
];

asort($list_url_visited); //配列をソート
$string     = implode(' ', $list_url_visited); //配列を文字列に結合
$id_visited = hash('md5', $string); //文字列をハッシュ化

オンラインで動作を見てみる@ paiza.IO

この行動パターンに固定長の ID を振れるメリットは機械学習などにも応用できます。

身近なところでは、リンクを開こうとして URL を見るとやたらとハッシュ値っぽいものがあるのを見たことがあると思いますが、アレです。

なぜなら、ハッシュ値は数値なので機械学習における「離散値」の特徴量としても使えるからです。

_{^{🐒 機械学習における「離散値」を簡単に説明すると、数値の大きい小さいに意味がないものや、数値と数値の差に関係がないものです。「リンゴは 1」「ミカンは 2」といった、特徴に ID 番号を振った数値のようなものです。}}

もちろんページ遷移だけでなく、5x5 ピクセルや 10,000x10,000 ピクセルといった、どんなサイズのピクセル・データにも固定長の ID を振ることもできます。

つまり、ハッシュ関数の特徴をよく理解すれば、アイデア次第でさまざまな活用方法がある関数でもあるのです。

そのハッシュ関数やハッシュ値の活用方法の例として「IPFS」と「ブロックチェーン」そして「NFT」をあげたいと思います。

ハッシュ関数と次世代ファイルシステム IPFS の関係

IPFS と言う用語を耳にしたことはあるでしょうか。以前から存在しているのですが、2020 〜 2021 年にかけて色々な理由で話題になったものです。

IPFS は Inter Planetary File System の略で、日本語に訳すと「惑星・・間ファイル・システム」です。

とても壮大な名前で、意味も不明です。しかし、内容はシンプルです。

従来の Web のファイル・システムが「場所」を指定してコンテンツを取得していたのに対し、IPFS は「内容」を指定してコンテンツを取得する、WEB 3.0 時代の新プロトコル。

「（自分で惑星とか言っちゃってるよ）」と感じるかもしれません。しかし、現在のインターネットの起源ともなった ARPANET も「Intergalactic Computer Network」（銀河・・間コンピューター・ネットワーク）が初期コンセプトにありました。

Web 3.0、はたまた Web3 という流行語
これから説明する「IPFS」「ブロックチェーン」「NFT」などは「Web 3.0 なんとか」と呼ばれることがあります。ここで注意して欲しいのが、同じ Web 3.0 と言っても、人によって意味合いが異なることです。
Google Map を皮切りに Ajax などが流行ったり、Wordpress などによって自分でブログを立ち上げたりできるようになった頃の Web 2.0 ブームを覚えている方も多いと思います。このブームを知っている人には「いよいよセマンティック・ウェブの時代（ティム・バーナーズ＝リーの Web3.0）が到来か」と思うかもしれません。
しかし、よくよく見ると「Web 3.0」ではなく「Web3」と表記が異なったり、なんかプライバシーの名の元にお金の臭いがちらついたり、何がすごいのか濁されている違和感を感じると思います。これは「Web 3.0」「Web3」「Web3（企業名）」と、すべてが別のものを指しているのに、根底にある「次の時代のインターネット」という共通項をネタにされているからです。
現在の「AI」しかり、何でも「デジタル」とつければ格好いいと言われた時代のように、「Web3」という用語を聞いたら、大半が「自分のビジネスのために事々しく言っている」と思って、警戒して聞いて良いと思います。各々の用語を理解しておけば、「技術」と「ビジネス」の境界線が見え、「あ、これは先物取引き的な勧誘だな」と気付けるはずです。

さて、「内容を指定してコンテンツを取得する」と言うのは「コンテンツのハッシュ値を指定して」と同義です。

百聞は一見にしかずなので、以下のリンクを別タブかウィンドウで開いてみてください。しばらくするとコンテンツが表示されると思います（この場合、"Hello, Qiita!" のテキスト）。

https://ipfs.io/ipfs/bafybeicd7b7mnnlnpvhv5kimfb5vedgslcwe5bgexj7olcszncnyzvp4oi

詳しくは後述しますが、上記の bafy...p4oi がコンテンツのハッシュ値を元に作られた CID と呼ばれるコンテンツの ID です。この CID を IPFS ⇆ HTTP のゲートウェイの 1 つである https://ipfs.io/ipfs/ にリクエストして、コンテンツを表示していることになります。

誰かが閲覧していた場合は、キャッシュが働いてコンテンツが即時表示されます。キャッシュの期限が切れていた場合、HTTP サーバーは IPFS ネットワークに問い合わせて表示します。同じ CID のコンテンツをシェア（PIN 留め）している最寄りの IPFS ノード、もしくは筆者の自宅にある RaspberryPi Zero のノードが問い合わせに反応し、数十秒ほど待つと表示されます。

ここで言うノードとは、P2P ネットワークにおけるピアと同義で、IPFS アプリが動いている端末（マシン）のことです。

サーバーであり、クライアントでもある端末をピアと呼びますが、他のピアから見てサーバー状態（リクエストを受け付けている状態）のピアをノードと呼びます（IN と OUT の接点と考えるといいでしょう）。そして同じサービスを提供しているノードの烏合の集をクラスタと呼んだりもします。この場合、IPFS クラスタです。

先述したように、この bafyb... から始まる数値が CID と呼ばれる、コンテンツのハッシュ値を元に IPFS の書式で表現したものです。

この値だけで Base32（32 進数）で表現された sha2-256 アルゴリズムを使ったコンテンツのハッシュ値を CID v1 の書式で記載したものである、ということがわかります。もちろん、ハッシュ値なので、この値からだけではコンテンツが "Hello, Qiita!" であることはわかりません。

CID インスペクタで、bafybei...p4oi から得られる情報を見てみる
- https://cid.ipfs.tech/#bafybeicd7b7mnnlnpvhv5kimfb5vedgslcwe5bgexj7olcszncnyzvp4oi

CID インスペクタの DIGEST (HEX): の値が、具体的な CID のハッシュ値なのですが、ローカルでファイルをハッシュ関数に通したものと異なることに気付いたかもしれません。

$ echo 'Hello, Qiita!' | sha256sum
5d3f0b287c036f5941a87a7589c8864d5259cdbf59673fe16681a2688baec652  -

$ echo 'Hello, Qiita!' | ipfs add --offline --only-hash --quieter --upgrade-cidv0-in-output
bafybeicd7b7mnnlnpvhv5kimfb5vedgslcwe5bgexj7olcszncnyzvp4oi

これは CID はファイルそのもののハッシュ値ではなく、負荷分散のためファイルを分割してハッシュ木で算出した最終的なハッシュ値に、各種エンコード情報を付加したものを CID（IPFS におけるファイルのハッシュ値）としているためです。このファイルを分割する仕組みは Merkle DAG と呼んでおり、インスペクタの MULTICODEC で確認できます。

次に、Brave などの ipfs:// プロトコルに対応したブラウザをお持ちの場合、以下のアドレスをアドレスバーにコピペして開いてみてください。

ipfs://bafybeicd7b7mnnlnpvhv5kimfb5vedgslcwe5bgexj7olcszncnyzvp4oi/

同じデータが表示されたと思います。

Brave ブラウザの IPFS 機能は拡張機能扱いになりました

デフォルトで IPFS が使えていた Brave だったのですが、残念ながら v1.69.153 (2024/08/22）から同梱されなくなりましたになりました。理由として誰も使おうとしないので本体の軽量化と開発負荷を減らすためのようです。おそらく IPFS を利用している人は、（Kubo などの）IPFS 本体をインストールして利用しているからと思われます。
今後は Chrome/IE/Firefox 同様、ブラウザの拡張機能で必要な人のみ機能を拡張して利用することになります。とは言え、標準で IPFS のバイナリは同梱されませんが、機能そのものは残っているため、自身で Brave をビルドし設定することで継続して使えます。ただし、拡張機能の方が（バグ修正含む）変更に追随しやすそうです。

「CDN？」「Etag？」「キャッシュ・サーバ？」と思うかもしれません。

まずは「どこにデータがあろうが、存在するならハッシュ値で取得できる」ことがポイントです。

File System と付いていたり、P2P 型であったり、「分散型ファイルシステム」と形容されるので、クラウド風のファイル・ストレージのようなイメージを受けますが違います。

どちらかと言うと git（分散型バージョン管理システム）と BitTorrent（分散型ファイル転送システム）を足して割ったようなものです。

「自分が共有しているファイルを、他の人も共有のサポートをしてくれるシステム」というイメージが近く、IPFS であっても自身のストレージは必要になります。

確かに「自分のストレージは持ちたくない」という場合であっても、git で言う GitHub、GitLab、Gitea のような有料 or 無料の範囲で外部サービスを利用することは可能です。

IPFS の外部ストレージ・サービスとしては Pinata などがありますが、クラウドや VPS などにデータを置き IPFS をインストールするなどの方法もあります。

しかし、忘れてはいけないのが git であっても IPFS であっても外部サービスを使った場合、「本来はローカル環境で管理するデータを、外部に委託してデータを置いているというだけ」ということです。災害時のリスク分散、メンテナンス、利便性を、お金で買っているという認識が大事です。

そのため、IPFS の外部サービスが落ちたり倒産するとデータは消えてしう（アクセスできなくなる）ということでもあります。WEB3 系の勧誘で「IPFS 上にデータがある限り、永遠にデータは消えません」という口上に「嘘は言っていないけど、ダークな誘導がある」と、お気付きでしょうか。

「分散型」を理解する

git の「分散型バージョン管理システム」をはじめ、IPFS の「分散型ファイルシステム」、後述するブロックチェーンの「分散型台帳」や NFT の「分散型所有権管理システム」といった、「分散型」という用語が多く出てきます。

注意しないといけないのは、分散型のメリットを過大解釈して、「分散型」を「非中央集権型」と言ってしまうことです。特に IPFS、ブロックチェーン、NFT を扱う企業やメディアが使いがちです。

しかし、同じ「分散型」の先輩である git パイセンの「分散型バージョン管理システム」を知る人は、GitHub がダウンするとニュースになるくらい依存しているのに「非中央集権型」とは変だとお気づきでしょう。

ここで改めて「分散型」という用語を認識する必要があります。

「分散型」（distributed）というのは「メインとなる何かを直接操作・処理しないで、コピーしたものを操作・処理するもの」を言います。

OS のイメージなど、コピーを配布することを英語で「distribute」と言いますが、配布されたものを使うイメージに近いものです。

そのため「拡散型」が適切な訳にも思えます。しかし、ローカルにコピー or 同期してから操作するので「メインがダウンしても、同じものが別の場所にある」という意味で「分散型」と呼ばれます。「リスク分散型」と捉えても良いでしょう。

そういう意味では git を「分散型バージョン管理システム」と呼ぶのがわかりやすい例です。

メインのレジストリ（例えば GitHub）がダウンしたとしても、コピーがローカルにあるので共倒れする（データがメインと一緒に飛ぶ）ことはありません。

本来は、それが git 本質なのですが、問題はローカルにも GIT サーバーを建てずに外部依存（GitHub に依存）してしまい、ユーザー自身が中央集権型にしていることなのです。

さて、IPFS の場合も、特定の共有ファイルを参照すると共有者に直接アクセスして参照せずに、一旦ローカルにコピーしてから参照します。

また、GitHub と GitLab をミラーリングするように、IPFS も参照したファイルをピン留めすることで（pin コマンドで、自分も再共有することで）単一障害点を少なくすることができます。

このように、共有者のマシンがダウンしても自身のローカルに残るため「分散型」と呼びます。

つまり将来、木星から地球のデータに IPFS で時間をかけてアクセスしたとしても、キャッシュ／PIN 留めをしておけば、同じ木星から誰かがアクセスした場合、そのキャッシュを使うことになるのです。これが IPFS が「惑星間うんぬん」と自称している理由です。

「... ...（NAS とかファイルサーバーを参照してプロキシとかでキャッシュするのと同じじゃん）」と感じると思います。

実際に似ています。しかし、IPFS のポイントは「特定の共有ファイルを参照する際の方法」です。

http:// や ftp:// はじめ afp:// file:// といったリソースを取得するプロトコルは、特定のサーバー上のファイルを取得するファイル・システムです。

これを、分散型にして「該当ハッシュ値のファイルを持っているマシンから取得する」というファイル・システムが IPFS プロトコル（ipfs://）です。

つまり「URL」や「ファイルのパス」を指定していたものが、「ハッシュ値」を指定してデータを取得するのです。

従来のプロトコル（コンテンツの場所を指定）

http://myhost.com/myusr/mydir/hello_qiita.txt
ftp://myhost.com/myusr/mydir/hello_qiita.txt

$ wget http://myhost.com/myusr/mydir/hello_qiita.txt
$ cat hello_qiita.txt
Hello, Qiita!

新プロトコル（コンテンツのIDを指定）

ipfs://QmSuyo747aBeA4yzXy354VUH3Z3pUBC3rULAQ5oF62fy5B
ipfs://bafkreic5h4fsq7adn5mudkd2owe4rbsnkjm43p2zm476czubujuixlwgki

$ # CID v0 フォーマットでリクエスト
$ ipfs cat QmSuyo747aBeA4yzXy354VUH3Z3pUBC3rULAQ5oF62fy5B
Hello, Qiita!

$ # CID v1 フォーマットでリクエスト
$ ipfs cat bafkreic5h4fsq7adn5mudkd2owe4rbsnkjm43p2zm476czubujuixlwgki
Hello, Qiita!

これは、IPFS は分散型であるため「だれ」（ホスト）や「どこ」（URL）を指定するのではなく、「なに」（ハッシュ値）を指定することを重視します。逆に「だれ」が重要になるのは、P2P で接続している相手になります。

具体的な IPFS の使い方は後述しますが、まずは同じ「ハッシュ値をベースにしたリポジトリ」同士である git と IPFS の共通点と違いを理解しましょう。

`git` と `IPFS` の相違点

分散型バージョン管理システムの git の場合、add と commit コマンドでローカルのリポジトリにファイルを登録すると、その版のハッシュ値（コミット ID、CID）が作成されます。

$ echo 'Hello, Qiita!' > hello.txt

$ git add .
$ git commit -m "initial commit"
[main (root-commit) 312eb0b] initial commit
 1 file changed, 1 insertion(+)
 create mode 100644 hello.txt

$ git log
commit 312eb0bf67d49b3107eaccaeb0b0f1fe3f0ae5a9 (HEAD -> main)
Author: KEINOS <github@keinos.com>
Date:   Sun Sep 15 18:58:04 2024 +0900

    initial commit

また、push すると登録したファイルが git レジストリ（GitHub や Gitea などの git リポジトリ置き場）に反映・公開（シェア）されます。そして他のユーザは pull した後、その CID（コミット ID）を叩けば同じ版を確認することができます。

分散型ファイル・システムの IPFS の場合も似ており、ファイルを add するとファイルがローカルのリポジトリに登録されハッシュ値（コンテンツ ID、CID）が作成されます。

$ echo 'Hello, Qiita!' > hello.txt

$ ipfs add hello.txt
added QmSuyo747aBeA4yzXy354VUH3Z3pUBC3rULAQ5oF62fy5B hello.txt
 14 B / 14 B [=========================================================] 100.00%

また name publish すると IPFS ネットワークに、自分がその CID を持っていることが公開されます。

$ # CID が QmSu...y5B のファイルを k2k...ci4 の公開鍵を持つノードから公開した例
$ ipfs name publish QmSuyo747aBeA4yzXy354VUH3Z3pUBC3rULAQ5oF62fy5B
Published to k2k4r8ovnhyqds4oh2ndfmzjn9oca0104ekiln8dive2pin83chpbci4: /ipfs/QmSuyo747aBeA4yzXy354VUH3Z3pUBC3rULAQ5oF62fy5B

そして、他のユーザは、その CID（コンテンツ ID）を叩けば同じ版のファイルを確認することができます。ちなみに、コミット ID もコンテンツ ID も、同じ CID と略されるのは偶然です。

_{^{🐒 IPFS で add からの name publish した自分は BitTorrent で言うところの「シーダー」となります。
BitTorrent の「シーダー」というのは、ファイルの全てのパーツを持っているピアのことを言います。「パーツ」というのも BitTorrent や IPFS は、ファイルが大きい場合 TCP/IP などのパケットようにデータを小さなパーツに分けて共有されます。これにより、ファイル全体を 1 つのピアから受け取らずに複数のピアから受け取れるため負荷分散できます。そして、すべてかき集めて完成したファイルを「シード」（種）といい、このファイルを共有しているピアを BitTorrent では「シーダー」と呼びます。
ちなみに P2P（Peer To Peer）などの「ピア」とは、サービスを利用 & 提供しているコンピュータのことで、1 台で「サーバー」であり「クライアント」でもあるものを言います。類似用語に「ノード」がありますが、「ピア」も「ノード」も同じです。違いは、ピアが他のピアからリクエストを受けた場合、つまりサービスを提供する（サーバ）状態のピアを「ノード」と言います。}}

さて、この時の git と IPFS の違いは、受け取った CID のコンテンツがローカルにない場合の動きです。

git は相手が pull もしくは fetch などでローカルを同期しておかないとコミット ID を受け取っても確認できないのに対し、IPFS の場合は CID を叩いてローカルに該当するファイルがない場合は IPFS ネットワーク上の他のピア（IPFS ノード）に問い合わせてローカルにキャッシュすることで確認できるようになります。

コンテンツ取得までの大きな流れは 5 ステップあります。「ルーターのパケットリクエストみたいなもの」と考えて読むとピンとくると思います。

コンテンツの CID を、接続しているピアたちに問い合わせる。
問い合わせを受けたピアは、そのコンテンツを持っている場合は、それを返す。
持っていないが、持っているピアを知っている場合、該当ピア（ノード ID）を知らせる。持っていないし知らない場合は、他の接続しているピアに問い合わせる。見つかった場合は、一時キャッシュして次回に活かす。
CID を持っているピアが特定できたら、該当ピアにコンテンツをリクエストして受け取る。データが大きいため分割化されている場合は、コンテンツの目録を受け取る。
受け取ったものが目録の場合は、接続しているピアたちに分割されたデータ（CID）を持っているか問い合わせる。（2 に戻る）
分散化されたデータを 1 つにまとめ、出力（表示 or 保存）する。

この時の「中間のピア」、つまりリクエストしたピアと、該当する CID のファイルを持っていたピアの「間にいる他のピア」の動きですが、皆が同じ動きをするのがポイントです。つまり、「ローカルになかったら他のピアに問い合わせる」です。

リクエストされた CID のファイル、もしくはその一部がキャッシュにある場合はリクエストしてきたピアにデータを渡す。
キャッシュにファイル、もしくはその一部がない場合は、さらに他のピアに問い合わせる。
見つけたらキャッシュして、リクエストしてきたピアにデータを渡す。

上記で「その一部が」というのは、ファイルが大きい場合は小さく分割されて管理されるからです。

BitTorrent でいう「リーチャー」（未完成のファイル、もしくは完成まであと一歩のリーチのかかったファイルを持っているピア）みたいなイメージです。

これにより「参照頻度の高いファイル」もしくは「その断片」は色々なピアにキャッシュされるため、総合的にダウンロードが速くなります。逆に「参照頻度の低いファイル」の場合、探し出すのに時間がかかります。ここらへんの動きも BitTorrent などと同じ感覚です。

そうなると、自分のピア（IPFS ノード）のキャッシュが「どの程度ストレージを圧迫するか」と、「ファイルを取得する速度がどの程度なのか」が気になります。

キャッシュ・ファイルの容量

デフォルト標準設定では IPFS は、IPFS リポジトリのあるローカル・ドライブ（パーティション）の空きがなくなるまでキャッシュされます。そして、容量がほぼ一杯になると、古くて参照頻度の低いキャッシュを削除していきます。macOS でいう TimeMachine と同じ考えです。

とは言え、このような Winny 時代にも問題でもあった「肥大化するローカル・キャッシュ」に対してガベージコレクションというオプション（--enable-gc）が用意されています。

IPFS デーモン（IPFS のサービス）を起動する際に --enable-gc オプションを付けると、ガベージコレクションが定期的に実行される設定になります。

デフォルトで 1 時間おきに 90 日以上参照されなかったキャッシュは削除され、自然淘汰されます。これらの時間や容量の設定は ipfs init で作成されたディレクトリ（リポジトリ）の config ファイル（~/.ipfs/config）を編集することで変更できます。

後述する ipfs.io や CloudFlare などが提供しているアクセスの多いピアは 24 時間経過してもアクセスのないファイルはキャッシュから削除しています。

また、BitTorrent で言う「シーダーになりたい」つまり「永続的にキープ（提供）したい」データの場合は 2 通りの方法があります。

普通にデータを IPFS リポジトリにコミット（ipfs add <CID>）する。
ipfs pin <CID> コマンドでキャッシュをピン留めしておく。

「ピン留め」とはキャッシュ・データに「削除しないフラグ」を立てることで、その CID を維持できます。

このように、IPFS は BitTorrent と git を足したようなものを公開専用のファイル置き場にしたものというのが、うっすらと見えてきたと思います。

IPFS の速度

IPFS にしたからといってファイルのダウンロードは速くはなりません。しかし、ローカルや、近いネットワークに別のピアを用意したり、CDN 、PIN サーバ（キャッシュ・サービス）を使うことで速くすることは可能です。IPFS のメリットは「誰かしらがファイルを持っていてくれたら必ず探し出せる」という点と、「しょぼいマシンで共有しても、使う人が多ければ多いほど負荷が下がっていく」の 2 点です。

分散型（P2P）の神話に「分散型にすると速くなる」があります。

分散型にすると速くなるというのは「特定の目線においては正しい」のですが、恵まれた環境、特に光回線が進んでいる日本国内においては必ずしも速くなるとは言えません。

「BitTorrent を使うとダウンロードが早いと聞いたのに、思ったより速くない」と感じた方も多いのではないでしょうか。

実は IPFS も同じです。

まず、アクセス頻度の低いファイルは、探し出すのに時間がかかります。そして、見つかった場合でも特定のピアからダウンロードされるため、そのピアのマシン・スペックや回線速度の影響をダイレクトに受けてしまいます。

逆に言えば、同じネットワーク内の別のピアにファイルがあった場合は、ローカル・ネットワークの速度でファイルをダウンロードできることになります。それでも大きなファイルは分割されて保存されているため、HTTP や FTP などのファイルの丸ごとダウンロードに比べると劣ってしまいます。

それでも IPFS を使うメリットは、災害時含めインフラが弱い（回線が遅かったり、高価なサーバーがない）ネットワークでも、負荷分散できることです。

また、昔の IPFS のサイトには「A peer-to-peer hypermedia protocol to make the web faster, safer, and more open.」といった記載があったので、「IPFS は速い」と勘違いされた経緯もあるようです。誤解を招くため現在は削除されています。

ここで言う faster とは、（CID がわかっていれば）「探し出すのが早い」という意味合いです。つまり「欲しいファイルがわかっているのに、どのサーバーにあるかわからないので、探すのに時間がかかる」という従来の問題に対して、「IPFS なら CID さえわかっていれば、どのサーバーにあるかは関係ない」という意味で faster と言っているのです。

じゃぁ BitTorrent と `git` でいいじゃん

良いと思います。しかし、IPFS は「WEB（http/https）の代替となる次世代プロトコル」を目指しており、名前だけでなく内容も野心的です。

「みんなで共有すればサーバいらない（高負荷に耐えるサーバじゃなくてもいい）じゃん」
「コンテンツの ID === hash(コンテンツの中身) なので改竄の心配ないじゃん」
「誰かのマシンにデータがあれば、消えることないじゃん」
「https と同じようにコンテンツ自体を暗号化しておけば公開ネットワークでもいいじゃん」

と、現在の Web サイトやインターネットの公開情報が持つ問題（例えばデータ改竄や DNS 改竄など）を、「ファイルのハッシュ値を使う」と言う、シンプルかつ大胆な新世代の情報ネットワークを作ろうと言うものです。

InterPlanetary File System @ Wikipedia
https://ipfs.io/ @ IPFS 公式サイト

IPFS と、その他のプロトコルの違い

何度か言及していますが、Web における HTTP や FTP などの従来のプロトコルと IPFS が根本的に違うのがコンテンツを取得する概念です。

Web（HTTP）の場合は、コンテンツの場所を指定してコンテンツを取得する、つまり「どこ」から取得するかが重要である。
IPFS の場合は、コンテンツの中身（ハッシュ値）を指定してコンテンツを取得する、つまり「なに」を取得するかが重要である。

もちろん、この IPFS プロトコル（仕様）以外にも HyperCore プロトコルや ICN など、似たアイデアはあり、多数存在します。

しかし、IPFS は

などにより、注目を浴びています。

何より 👌予算の使い方が上手く、issue やドキュメント作成に対して懸賞金をかけることでコミッターに還元したりしているので、他のプロトコルよりドキュメントが整っていて使いやすい印象を受けます。

そのため、数あるコンテナ技術のうち Docker が一強になったように、公開分散ファイルシステムの Docker 的なメジャーなものになりつつあります。（たぶん。知らんけど）

つまり、今後はブラウザのアドレスに ipfs://<IPFSハッシュ値> と打てば、このハッシュ値のファイルを持った最寄りのノード（ipfs を立ち上げているマシン）から取得されるようになるのです。このファイルが HTML の場合は静的 Web サイトが表示され、ZIP などのアーカイブの場合はダウンロードが始まると言うことです。

実際に 2021/05/20 現在の時点で Brave ブラウザやモバイル版 Opera ブラウザは標準で実装済みで、Chrome・Firefox・Edge は拡張機能／アドオンをインストールすることで使えるようになります。

IPFS の URI 例:
- ipfs://bafkreicnzih5l5beumnqhk4aps5oo7vtfpznbcpo2hhocvftv7wuldpa3q
  _{^{（Brave などの対応ブラウザもしくはプラグインを入れて URI を開いてみてください。"hello, world!" と、以下の URL と同じコンテンツが表示されるはずです）}}
- https://ipfs.io/ipfs/bafkreicnzih5l5beumnqhk4aps5oo7vtfpznbcpo2hhocvftv7wuldpa3q
  _{^{（この https://ipfs.io/ipfs/ については後述）}}

IPFS の使い勝手

さて、ここからが Qiita 的に IPFS の真骨頂です。つまり「IPFS の使いやすさは、いかほどのものか」というところです。

IPFS 自体はプロトコルなので、それらを使えるように実装されたプログラムが提供されており、大きく GUI 版と CUI 版がります。

CLI で動かせる CUI 版には Go 言語で実装した Kubo（旧 IPFS）と、Javascript で実装された js-ipfs があります。

そして CLI が苦手なら、GUI 版の IPFS デスクトップ版や、ブラウザの拡張機能があります。

Brave などの、ブラウザによっては標準で実装されているものがあります。Brave ブラウザの場合、アドレス欄に「brave://ipfs」と打って「開始する」ボタンを押すと表示される「マイノード」でもデスクトップ版と同じものが表示されます。

とは言え、「IPFS のデスクトップ版」と言っても Electron ベースで、同梱されている ipfs コマンド（Kubo）のビルトイン Web サーバーを表示しているだけなのです。

実は ipfs コマンド（Kubo）はビルトイン Web サーバーを内蔵しているので、これらはそれを表示しているだけなのです。

ブラウザの機能拡張では js-ipfs（Javascript 実装）が使われ、IPFS Desktop では　Kubo（Go 言語実装）が使われている程度の認識でいいでしょう。そして Electron の重さが気になる人は ipfs コマンドを使い、ビルトイン Web サーバーを使うといいでしょう。

さて、この ipfs コマンド（Kobo）は Go 言語で書かれているため、ビルドされたバイナリは単体のプログラムとして動きます。

go-ipfs | Distributions @ IPFS

つまり、ipfs.exe や ipfs のバイナリをパスが通った先に設置するだけなので、使うのにアレコレとインストールする必要がないのです。

もちろん、手動インストールやアップデートの更新が面倒な人のために brew や choco などのパッケージマネージャー経由でインストールも可能ですし、ipfs-update という ipfs のインストール & アップデート専用ツールもあります。ダウンロードして実行するだけでインストールや更新をしてくれます。

さて、CLI 版（コマンド）の使い勝手ですが、git に似ているものの git より直感的です。

実際に触ってみれば、おそらく「え？これで動くの？」と思うことでしょう。

以下のコマンド・ラインでの実行例をザッとご覧ください。

IPFSコマンドの利用例

$ ipfs --version
ipfs version 0.7.0

$ # ipfs リポジトリの初期化。通常 ~/.ipfs に作成される。（専用の秘密鍵＆公開鍵、リクエストした
$ # ファイルのキャッシュなどの置き場）
$ ipfs init

$ # ipfs デーモン（同期機能）の起動。バックグラウンド実行とログ出力付き。これで P2P の 1 つの
$ # ピアとして起動する。
$ ipfs daemon > ipfs.log &

$ # ipfs ネットワーク上もしくはリポジトリ上にあるファイルを開く。ネットワーク上にあった場合は、リポジ
$ # トリにキャッシュする。
$ ipfs cat bafkreicnzih5l5beumnqhk4aps5oo7vtfpznbcpo2hhocvftv7wuldpa3q
hello, world!

$ # 新規サンプル・データの作成（データはテキストに限らず画像などのバイナリでも問題ない）
$ echo 'Hello, Qiita!' > hello.txt

$ # リポジトリにデータ追加。追加したデータのハッシュ値（CID）が返される。
$ ipfs add hello.txt
added QmSuyo747aBeA4yzXy354VUH3Z3pUBC3rULAQ5oF62fy5B hello.txt
 14 B / 14 B [=== ... ===] 100.00%

$ # リポジトリ内のデータ（CID）の公開および通知。戻り値は公開したノードの ID（IPNS の Key）と公開
$ # した内容。
$ ipfs name publish QmSuyo747aBeA4yzXy354VUH3Z3pUBC3rULAQ5oF62fy5B
Published to k51qzi5uqu5dloao8jzqletz2tz06su210ddl0hn7vwo5hoi1an40zs57wjh3y: /ipfs/QmSuyo747aBeA4yzXy354VUH3Z3pUBC3rULAQ5oF62fy5B

$ # 公開したファイルの確認（他のマシンで確認してもよい）
$ ipfs cat QmSuyo747aBeA4yzXy354VUH3Z3pUBC3rULAQ5oF62fy5B
Hello, Qiita!

$ # IPFS ネットワークを HTTP に転送するゲートウェイ経由であれば cURL でも取得できる
$ curl https://ipfs.io/ipfs/QmSuyo747aBeA4yzXy354VUH3Z3pUBC3rULAQ5oF62fy5B
Hello, Qiita!

$ # データを公開した際に得たノードの ID（IPNS の Key）でゲートウェイ経由で cURL してみる
$ curl https://ipfs.io/ipns/k51qzi5uqu5dloao8jzqletz2tz06su210ddl0hn7vwo5hoi1an40zs57wjh3y
Hello, Qiita!

$ # ローカルの HTTP ゲートウェイ経由でファイルを取得（ipfs デーモンが簡易 Web サーバの機能を
$ # 持っています）
$ curl http://localhost:8080/ipfs/QmSuyo747aBeA4yzXy354VUH3Z3pUBC3rULAQ5oF62fy5B
Hello, Qiita!

上記のように、意外に簡単に公開分散ファイルシステムが使えてしまいます。

途中で https://ipfs.io/ipfs/<CID> や https://ipfs.io/ipns/<Key> でもアクセスできることに「（おっ！curl や wget でも使えるってか！）」と感じたかもしれません。

https://ipfs.io/ipfs/ は IPFS ネットワークを HTTPS につなげるゲートウェイの 1 つです。自分でも建てられますし、CloudFlare などの CDN プロバイダーも建てています。

オンラインで上記のコンテンツを表示してみる
- https://ipfs.io/ipfs/QmSuyo747aBeA4yzXy354VUH3Z3pUBC3rULAQ5oF62fy5B @ ipfs.io
- https://cloudflare-ipfs.com/ipfs/QmSuyo747aBeA4yzXy354VUH3Z3pUBC3rULAQ5oF62fy5B @ cloudflare-ipfs.com

CDN を通すと何が良いかというと、キャッシュされていれば CloudFlare の速度で Web サーバー・レスで静的ファイルを提供できるということです。つまり後述する Raspberry Pi や使っていない PC などにコンテンツを突っ込んで IPFS 上で共有して、定期的に URL を叩いておけば、CDN を通して提供できるということです。

ファイルの更新

若干の復習ですが、CID は実質的にコンテンツの内容のハッシュ値なので、コンテンツの内容が変わるたびに CID も変わります。

つまり「そのコンテンツの ID」と言うよりは「そのコンテンツの版（バージョン）の ID」という表現が似合うかもしれません。git で言うところのコミット ID（CID）や、Docker で言うイメージレイヤーのハッシュ値（Image ID）と同じです。

これによりデータの一意性が増すのですが、逆にデータの内容を更新して共有したい場合には CID は適しません。何かを更新するたびに新しい CID を相手に伝えないといけないからです。

この問題を解決する方法の 1 つが IPNS（InterPlanetary Name System）です。

IPNS とは

IPNS（InterPlanetary Name System）は、名前に CID を紐づける仕組み。

これを活用してディレクトリを紐づけるとコンテンツを更新しても変わらない一意のアドレスを作ることができる。

IPNS を完全に理解した気になるためには ipfs name コマンドは何をするのか理解しないといけません。なぜ name なのか、と。

_{^{🐒 説明が長ったらしいので「IPNS は IPFS の PKI の名前空間で、ノードの公開鍵のハッシュ値を名前（Key）に、CID と、ノードの秘密鍵による CID の署名と、公開鍵を Value にして空間に設置し、ディレクトリを CID にすることでディレクトリ内の複数ファイルを共有できる」と言われてピンとくるせっかちさんは次の章に進んでください。私には何を言っているかわからなかったので、この章では、これをかなり咀嚼そしゃくしながら説明します。}}

まずは具体的な動きを見ながら逆算して（紐解いて）いった方が、ちょっとできるくらいには理解できるかなと思います。

コンテンツを登録して、その CID を公開すると、最終的に 2 つのハッシュ値が得られます。① /ipfs/Qm から始まるハッシュ値と、② k5 から始まるハッシュ値です。

下記ログの、ipfs add コマンドと ipfs name publish コマンドで得られた各々のハッシュ値に注目ください。

コンテンツの登録と公開

$ # コンテンツの登録（データをリポジトリに追加。そのハッシュ値が確認できる）
$ ipfs add hello.txt
added QmSuyo747aBeA4yzXy354VUH3Z3pUBC3rULAQ5oF62fy5B hello.txt
 14 B / 14 B [=== ... ===] 100.00%

$ # 追加したリポジトリ内のデータの公開。戻り値はコンテンツの IPNS の Key とコンテンツの IPFS URI
$ ipfs name publish QmSuyo747aBeA4yzXy354VUH3Z3pUBC3rULAQ5oF62fy5B
Published to k51qzi5uqu5dloao8jzqletz2tz06su210ddl0hn7vwo5hoi1an40zs57wjh3y: /ipfs/QmSuyo747aBeA4yzXy354VUH3Z3pUBC3rULAQ5oF62fy5B

2 つ目のコマンド実行結果にある、最初が k5 から始まるハッシュ値ですが、これが IPNS の仕組みだけでなく IPFS の P2P ネットワークが構築される上で重要な役割を果たします。

CID が「何what」（コンテンツの中身）を示すハッシュだとすると、k5 から始まるハッシュは「誰who」（ピアのノード ID）を示すハッシュなのです。

ipfs name publish のコマンドの意味を、もう少し掘り下げましょう。

登録したコンテンツを公開するコマンド

ipfs name publish QmSuy...中略...fy5B

上記コマンドは、日本語だと
「このノードの名nameにおいて、コンテンツ QmSuy...中略...fy5B を公開publishせよ！ipfs!」
という意味になります。

そして、実行結果は以下のようになります。

Published to k51qz...中略...jh3y: /ipfs/QmSuy...中略...fy5B

上記レスポンスは「k51qz...中略...jh3y に /ipfs/QmSuy...中略...fy5B を公開しました」という意味になります。

IPFS 上の各々のピアは、name と呼ばれる情報のフィールド（項目）を持っています。この値は、各ノードの公開鍵をハッシュ化した値で、これが上記の k5... から始まる値です。そして、この値がノードの ID になります。

上記 Published to ... というレスポンスは、厳密には「ノード ID k51qz...中略...jh3y の秘密鍵で /ipfs/QmSuy...中略...fy5B を署名して、他のノードに公開している旨を通知しました」という意味になります。

逆に言うと、ノード名 k51... にアクセスすると、そのノードが公開している（署名された）ファイルにアクセスできるということでもあります。

これが IPN・S の /ipns/k51qz...中略...jh3y でも取得できる理由です。（詳しくは後述）

このように、特定の IPFS ノードからデータを引き出すために使われるため、ipns で指定するノード ID（name）の値は Key と呼ばれます。変数が Value（価値）を引き出すために Key を指定するようなものです。

概念より、具体的な流れで見てみましょう。「理解した」というかたは、すっ飛ばして構いません。

この Key を使って、ひと工夫するとコンテンツが更新されても変わらないアドレスが作成できます。先に「ひと工夫」の答えを言ってしまうと「ディレクトリを共有する」ことです。

その「ひと工夫」の前に、先ほど公開したコンテンツにアクセスしてみましょう。実際の動作を見ることで、復習もかねて、より正確に理解できます。

まずは CID を使った /ipfs/<CID> でアクセスする方法と、IPNS を使った /ipns/<Key> でアクセスする方法です。どちらも同じ内容が返って来ます。

$ # IPFS の CID でアクセス
$ curl https://ipfs.io/ipfs/QmSuyo747aBeA4yzXy354VUH3Z3pUBC3rULAQ5oF62fy5B
Hello, Qiita!

$ # IPNS の Key でアクセス
$ curl https://ipfs.io/ipns/k51qzi5uqu5dloao8jzqletz2tz06su210ddl0hn7vwo5hoi1an40zs57wjh3y
Hello, Qiita!

次に、同じ手順で同じファイルを更新（内容を書き換え）して、再度公開してみます。つまり、ipfs add で CID を発行したのち、その CID を ipfs name publish で公開します。

この時、Published to の前半の k5 から始まるハッシュ値（Key）は変わらないことに注意します。

同じhello.txtに違う内容を上書き

$ # コンテンツの変更（内容の書き換え）
$ echo "Hello, I'm KEINOS!" > hello.txt

$ # 変更コンテンツの登録
$ ipfs add hello.txt
added Qme36EKDmxfnhWhFcZQ7pZUnoCLCinxNShS66JwM7z4Fvx hello.txt
 19 B / 19 B [=== ... ===] 100.00

$ # 変更コンテンツの公開（更新の反映）
$ ipfs name publish Qme36EKDmxfnhWhFcZQ7pZUnoCLCinxNShS66JwM7z4Fvx
Published to k51qzi5uqu5dloao8jzqletz2tz06su210ddl0hn7vwo5hoi1an40zs57wjh3y: /ipfs/Qme36EKDmxfnhWhFcZQ7pZUnoCLCinxNShS66JwM7z4Fvx

そして同様に、公開されたコンテンツを cURL で確認してみます。IPNS（/ipns/<key>）でアクセスする方は Key の値が変わっていないことに注目します。

$ # IPFS の CID でアクセス（内容が変わったので、当然 CID も変わる）
$ curl https://ipfs.io/ipfs/Qme36EKDmxfnhWhFcZQ7pZUnoCLCinxNShS66JwM7z4Fvx
Hello, I'm KEINOS!

$ # IPNS の Key でアクセス（内容が変わったのに Key は変わっていない）
$ curl https://ipfs.io/ipns/k51qzi5uqu5dloao8jzqletz2tz06su210ddl0hn7vwo5hoi1an40zs57wjh3y
Hello, I'm KEINOS!

どちらも同じ変更された内容になりました。つまり /ipns/<Key> を使うと同じアドレスが使えることがわかりました。

しかし、1 つ落とし穴があります。

「別のファイルと内容」で、同じように登録 & 公開してみましょう。今度はファイル名を hello.txt から greetings.txt に変えて、内容は定番の "Hello, world!" にしてみます。

新規コンテンツの登録と公開

$ echo "Hello, world!" > greetings.txt

$ ipfs add greetings.txt
added QmeeLUVdiSTTKQqhWqsffYDtNvvvcTfJdotkNyi1KDEJtQ greetings.txt
 14 B / 14 B [=== ... ===] 100.00%

$ ipfs name publish QmeeLUVdiSTTKQqhWqsffYDtNvvvcTfJdotkNyi1KDEJtQ
Published to k51qzi5uqu5dloao8jzqletz2tz06su210ddl0hn7vwo5hoi1an40zs57wjh3y: /ipfs/QmeeLUVdiSTTKQqhWqsffYDtNvvvcTfJdotkNyi1KDEJtQ

当然のように CID は変わったのですが、Key は変わっていません。

するどい人は「（あ〜、なるほど）」と、お気づきかもしれません。鈍にぶチンの私は、公開コンテンツにアクセスして「えっ？」となるまでわかりませんでした。てへ

早速、新規公開コンテンツにアクセスしてみましょう。

新規公開コンテンツにアクセス

$ # IPFS の CID でアクセス（CID が変わったが、当然内容も変わる）
$ curl https://ipfs.io/ipfs/QmeeLUVdiSTTKQqhWqsffYDtNvvvcTfJdotkNyi1KDEJtQ
Hello, world!

$ # IPNS の Key でアクセス（Key は変わっていないが、内容が変わった）
$ curl https://ipfs.io/ipns/k51qzi5uqu5dloao8jzqletz2tz06su210ddl0hn7vwo5hoi1an40zs57wjh3y
Hello, world!

なんと、先ほどの Hello, I'm KEINOS! が上書きされてしまいました！

つまり、ターゲットとなるファイルは関係なく IPNS の Key でアクセスできるのは最後に登録された CID のみということです。

1 ページものの静的 Web ページを公開するなら良いのですが、これでは複数ファイルには使えません。かといって、コンテンツごとに別の IPFS ノード（IPFS のデーモン）を用意するのも非合理です。

実は、この Key の値は現在の「ノードの公開鍵Key」をハッシュ化した値です。そのため、何を登録しても Key の値は変わらなかったのです。

$ ipfs name publish <CID>
Published to <Key>: /ipfs/<CID>

IPNS の NS は Name System とは言うものの、どちらかと言うと Name Space の System（名前空間の仕組み）と考えるとしっくりきます。

IPFS ネットワークには IPNS という名前空間があり、この Key のハッシュ値を「ノードの名前（name）」として使います。

そして、各々の name は Key-Value 型の連想配列のようになっており、値（Value）は 3 つの要素で構成されています。

ノードの公開鍵
CID
CID をノードの秘密鍵で署名した証明書

つまり ipfs name publish <CID> というのは、「コンテンツの公開」と言うよりは、厳密には「コンテンツを署名した name の公開」なのです。

具体的には、ipfs name publish <CID> を実行すると、ノード（name）の「秘密鍵」で CID を署名して IPFS ネットワークに公開（publish）する」というコマンドなのです。

これが /ipns/<Key> でアクセスすると上書きされてしまう原因です。ipfs name publish によって証明している CID が変わってしまったからです。

ここで、いったん落ち着いて「複数の CID を公開する」場合を考えると、2 つの方法が考えられます。

ipfs name publish する際に複数の CID を指定する。
コンテンツごとに新しい公開鍵と秘密鍵のペアを作成して使う。

前者は、ディレクトリに複数コンテンツを入れておき、ディレクトリを ipfs add することで、まとめて 1 つの CID にできます。また、1 つの鍵のペアで済むため、管理が楽になります。

しかし、全てが同じグループ（ディレクトリ）になってしまうため、異なる内容も含めてしまうと、ファイルやディレクトリ構成が煩雑になるというデメリットもあります。（ちなみに、ディレクトリ下のファイルにアクセスするには /ipns/<Key>/<ファイル名> とファイル名でアクセスできます）

後者は、管理は煩雑になりますが、前者の「ディレクトリ」の仕組みと組み合わせると、内容のグループごとに鍵のペアを作成しておけば、ファイルやディレクトリ構成が綺麗になるというメリットがあります。

_{^{🐒 ちなみに鍵のペアを作成するコマンドは ipfs key gen です。詳しくは ipfs key --help をご覧ください。}}

Web3.0 時代の Web サーバを建てずに Web サーバを建てる

この、ipfs name publish によるディレクトリの公開を、CDN と従来の DNS の仕組みに紐づければ、公開 Web サーバを建てなくても高パフォーマンスの Web サーバを建てることができるのです。

「建てなくても建てられる」とか、何を言っているのかと思うかもしれません。

先に一言で言ってしまうと「HTTP ゲートウェイ自体が Web サーバーだから」です。

つまり、公開したいコンテンツの IPFS ノードさえ立ち上げておけば、HTTP ゲートウェイ経由でアクセスできるのです。そして、HTTP ゲートウェイが CDN であれば、2 度目以降のアクセスはキャッシュされるので、自分のノードの負荷を減らせます。

何はともあれ、Wikipedia 英語版の 2016 年のスナップショットをご覧ください。ipfs.io cloudflare-ipfs.com どちらの HTTP ゲートウェイからでもアクセスでき、同じ内容を参照できますが、どのノードにあったコンテンツかはわからないことに注目です。

ipfs://QmXoypizjW3WknFiJnKLwHCnL72vedxjQkDDP1mXWo6uco/wiki
- https://ipfs.io/ipfs/QmXoypizjW3WknFiJnKLwHCnL72vedxjQkDDP1mXWo6uco/wiki/
- https://cloudflare-ipfs.com/ipfs/QmXoypizjW3WknFiJnKLwHCnL72vedxjQkDDP1mXWo6uco/wiki/

とは言え「静的ページだし ... CID 叩いてるだけだし ... まぁ、そうだよね」という感じでしょう。

やはり、ドメイン依存の我々からすると俺様ドメイン独自ドメインで ipns/<KEY> を公開したくなります。

例えば、俺様ドメインの https://oresama.sample.com/ にアクセスすると /ipns/<MyKey>/ で共有している俺様ディレクトリを参照させる、といったことです。

後述しますが IPFS ノードは RaspberryPi Zero でも建てられます。また、前述したように IFPS デーモンは標準で HTTP ゲートウェイ（IPFS → HTTP）を持っているので、自宅のルーター設定で俺様 IPFS ノードに HTTP ポートを向けて解放して、Dynamic DNS ツールなどを使えば公開できます。

しかし、この HTTP ゲートウェイを公開して共有するのは昔ながらの自鯖（自宅サーバ）の方法です。

つまり、ルータの設定や自鯖のパフォーマンスが問われ、何より不特定多数が自宅のルーター経由でアクセスしてくるため避けたいものです。

HTTP の世界において、アクセス過多や不正なアクセスを防ぐ 1 つの方法が CDN を利用することです。これを俺様ノードのゲートウェイ（出入り口）として活用するのです。

つまり、フロントエンドを CDN に設定することで、自分のノードにリクエストするのは CDN だけに絞られ、キャッシュ・サーバーとして働くので自分のノードの負荷は減ります。つまり、ラズパイ Zero 程度のマシンでも、サーバーを建てられるのです。

「（いや。サーバ公開してんじゃんwww）」と思うかもしれません。... ... 確かに。

でも、自宅では IPFS のノードだけで、外部に HTTP のポートを公開していないことに注目です。

CloudFlare を例にすると、以下のような設定をします。

俺様ドメインの DNS 設定
1. CNAME を CloudFlare の HTTP ゲートウェイに向ける（cloudflare-ipfs.com）
2. TXT に dnslink=/ipns/<MyKey> を追加する
  - 参考: Connecting Your Website | IPFS Gateway @ developers.cloudflare.com

これだけで、https://mydomain.com/sample.html とアクセスがあった場合、https://cloudflare-ipfs.com/ipns/<MyKey>/sample.html にアクセスした場合と同じになります。そして CloudFlare は ipns/<MyKey> が共有している sample.html を取得 & キャッシュし表示します。

この仕組みを DNSLink と言います。

この時のポイントは、俺様 IPFS ノードがあるネットワークのルータの設定をいじる必要が（基本的に）ないことと、一度アクセスすれば CloudFlare だけでなく IPFS ノードから自宅までの中間の IPFS ノードにキャッシュされることです。

つまり、低いスペックのマシンでも専用機にするなら IPFS デーモンを十分走らせることができます。

何より、CloudFlare 経由の HTTP 接続でなくても IPFS 対応のブラウザなどで /ipns/<MyKey>/sample.html とアクセスする際も CloudFlare のノードのキャッシュを使ってくれるなど、いいとこ取りです。

「（でも静的ページのみで動的ページのコンテンツは公開できないじゃん）」と思うかもしれません。そういう方は WebAssembly を掘り下げてみてください。

外部に向けたサーバを建てなくてもコンテンツを公開できるこの IPFS の仕組みから、何か色々と見えて来たのではないでしょうか。

さらに、この IPFS の技術と、後述するブロックチェーンと組み合わせるなど、なさらなる色々な技術（マッシュアップ）が産まれようとしています。

いよいよティム・バーナーズ＝リーさんの言う「セマンティック・ウェブ」もしくは Web 3.0 の時代が来つつありそうです。たぶん。知らんけど。

プライベートな IPFS ネットワーク

IPFS は、基本的に公開文書向けのネットワークとして始まったのですが、やはり「プライベートな分散ファイルシステムとして使いたい」と思うかもしれません。

基本的には可能ですが、プライベート IPFS は、どちらかと言うとハッシュの話しより、暗号寄りの話しなので割愛しますが 3 行で説明します。

IPFS のリポジトリ（.ipfs）直下に共通鍵を置くと通信を暗号化することができる。
同じ共通鍵を持つ（設置した）ピア同士で仮想的なネットワークが作れる。（HTTPS や VPN と似た発想）
共通鍵は ipfs-swarm-key-gen コマンドで作成する。

参考文献: IPFS Tutorial: Building a Private IPFS Network with IPFS-Cluster for Data Replication @ eleks

IPFS はラズパイ Zero(W) でも動く

「（IPFS 試してみたいけど、ローカルに入れるには、いささか躊躇ちゅうちょしてしまうな）」という方には、2千円程度で手に入る RaspberryPi Zero W で試されてはいかがでしょう。

Linux と SSH 接続の知識が必要ですが、IPFS 専用機にチューニングすれば十分に使えます。

主なチューニング内容
- GUI なし (RaspberryPi OS Lite)
- 解像度低め
- GPU メモリ割り当て少なめ
- スワップサイズ 2GB

GitHub に IPFS のインストールとアンインストールのスクリプトを置いてありますので、よろしければご覧ください。

IPFS Installer for RaspberryPi Zero W | IPFS-RPi-Zero @ GitHub
参考資料
- IPFS の Qiita 記事 @ Qiita カテゴリ
- IPFS 入門 @ decentralized-web.jp
- Raspberry Pi Zero W の価格 @ スイッチ・サイエンス
- ヘッドレス RaspberryPi ZeroW のブートディスク作成（Wi-Fi 設定済み SSH 有効済み）と設定 @ Qiita
- QiiCipher | GitHub 上の公開鍵を使ってファイルの暗号化と署名確認、ローカルの秘密鍵で復号や署名をするシェル・スクリプト @ GitHub

ハッシュ関数とブロック・チェーンの関係

ブロックチェーンの今北産業
1. 分散型の追記専用データベースである。
2. 既存データの変更（改ざん）防止は、上書き禁止といった設定や運用ではなく、仕組みそのもので追記しかできないようになっている。
3. 分散化および検証への貢献にインセンティブを設けることで、データの永続化が期待できる。

さて、ちょいちょい出てきた、仮想通貨（暗号資産）で有名なブロック・チェーンですが、その仕組みのベースに使われているのもハッシュ関数です（ハッシュ関数の特徴に関しては前述の「ハッシュ関数の基本と特徴」参照）。

ブロック・チェーンを、恐れずに一言で表すと「実質的に変更や改竄かいざんができない分散型のログ変更履歴」です。

もしくは「一度書き込んだら変更できない、追記と読み取り専用のデータベース」です。

変更を行いたい場合は、住民台帳や銀行の口座などと同じで「追記により調整」します。例えば、7 というデータを 5 に変更・修正したい場合は、-2 というデータを追加して調整します。

この追記型の記録方式を「台帳」と呼びます。ブロック・チェーンを「分散型台帳・・」とも呼ぶのは「変更は追記のみによって行う」という台帳の概念と同じだからです。

つまり、一度書き込んだデータは読み取り専用になるという機能自体は、CD-R のような、35 年以上前からある WORM (Write once read many) と変わりがありません。

そして「分散型ロギング・システム」と呼ばれないのは、そのログ（記録）に「紐付けたいデータのハッシュ値」を記録することで外部データとの紐付けも行えるからです。

しかし、そこ（ハッシュ値によるデータの紐付け）がブロックチェーンにおけるハッシュ関数のキモではありません。分散型で紐付け式に特化した DB 自体は etcd などに代表される KVS があるからです。

後述しますが「実質的に変更や改竄かいざんができない仕組み」の実質的な部分にハッシュ関数が使われています。

ブロックチェーンとgit

さて、変更を積み上げていくという意味でも、git（分散型バージョン管理システム）などと同じ「変更履歴の DB」の一種と考えると良いでしょう。

しかし、ブロックチェーンの場合は、git などのように --amend と懺悔ざんげして過去を無かったことに仕組み上できません（変更できない仕組みも後述します）。

また「分散型・・・台帳」の「分散型」というのは「データをメインからローカルに同期してから使う参照する」「データの追加はメインにリクエストして、メインが行う」という意味です。

これも git と理屈は似ています。

リモート・リポジトリを直接参照するのではなく、ユーザーは同期されたローカル・リポジトリを参照し、変更はリモート・リポジトリにリクエストして、無事マージ反映されると他の人にも同期されていくのと同じです。

マージ（変更の追記）ですが、git の場合、マージ権限を持つのはリポジトリのオーナーや、権限をもつコラボレーターです。

ブロックチェーンの場合は、参加しているノードのうち「リーダー」と呼ばれるノードが追加の処理を代表して行います（リーダーは多数決により適宜決まります）。そして他のノードは、リーダーの DB 変更に追随して、ローカルの DB を参照します（ノードとは、ここでは DB を管理しているマシンを指します）。

また、マージ前の追記内容の確認（レビュー）ですが、git の場合は、マージ権限を持った管理者が行います。ブロックチェーンの場合は、CI による自動マージに近いです。リクエストされた追記内容（数値の増減など）に不等号がないと他のノードから判断された場合は、早い者勝ちで登録（追記）されます。

この時の「不等号がないか」の確認は、サービスによって異なります。

例えば、ブロックチェーンが仮想通貨などの暗号資産のサービスに使われている場合は、「口座残高を確認する」などの確認です。

実際の確認は自動で行われますが、手動でも確認可能です。暗号資産の DB（ブロックチェーン）そのものをダウンロードして確認してもいいのですが、データサイズが大きかったり、DB クラスターの一員にならないといけないなど、煩雑です。

たいていのブロックチェーンは API を提供しているので、Web API を経由して確認するのが、手動の場合は楽でしょう。その 1 例として、Solana のブロックチェーンを利用した暗号資産の 1 つである SOL の筆者の口座をご覧ください。

KEINOS の SOL ウォレットをオンラインで見る @ explorer.solana.com

2023/02/27 現在、たったの 1.19 SOL しか残高がないことが確認できます。また、History で口座間の移動の履歴も確認できます。

ここでは、仮想通貨うんぬんではなく、ブロックチェーンの仕組みにより、この History は「追記はできても変更や改竄かいざんはできない」という点に注目してください。

ブロック・チェーンでは「変更不可能」を実現するために、以下の３つのハッシュ関数の特徴が活かされています。

非可逆である（元に戻せない）
同一性（同じものであること）が確認できる
衝突を探すのは大変だが、探したものを確認するのは簡単

ここで言う「衝突」とは「異なる値なのにハッシュ値が同じになっちまった」という状態です。業界用語で collision と言い、発音はチョッと照れる感じで「これじゃん？」寄りに「コリジョン」です。

しかし、ブロック・チェーンの何が「すごい」のでしょう。

「中央集権型に依存しなくていい」とか「お金に変わる何とか」とか聞きます。しかし、エンジニアを続けていると peer-to-peer（or 分散型）が必ずしも良いわけではないことを体感していたり、メンコとかトレーディングカードとかと何が違うのか、と。パチンコやスロットの換金コインと何が違うのか、と。「世間との熱量の違い」を感じてしまいます。

恐らく、エンジニア的にブロック・チェーンが面白いのは「ビザンチン将軍問題」もしくは「二人の将軍問題」を解決できることかもしれません。

ビザンチン将軍問題 @ Wikipedia
二人の将軍問題 @ Wikipedia

「ビザンチン将軍問題」「二人の将軍問題」の概要

「ビザンチン将軍問題／二人の将軍問題」は、一言で説明すると「A から B へ情報を伝達するルートが信用できない場合に、正しい情報を伝えることができるか」という問題です。

おおざっぱにサーバーで例えると以下のイメージです。

A 国にサーバー A 、B 国にサーバー B があり、お互いの準備が整うと各々「処理 X」を始めます。しかし、どちらかの準備が整っていないで「処理 X」を始めると、核核然然かくかくしかじかな理由で「両国が崩壊する」と仮定します。

問題は A 国と B 国のネットワークが複数の国を経由しないといけないことです。

その経由先には敵対する C 国があるだけでなく、寝返る「かも」しれない同盟国 D 国と E 国もあります。「寝返る『かも』」と言うのは、D 国も E 国もお賃金が安く、役人でさえ小遣い稼ぎで賄賂をもらうような人が多い国である、という設定です。

「準備ができていない」と伝えたのに「準備できた」と伝わってしまった場合、両国が崩壊します。つまり敵対国は中継経路で改ざんするのが狙い目であるため、同盟国といっても安心できないのです。

この、「準備が整った」と伝達するルートの途中で改ざんされる可能性があるのが最大の問題です。

途中の経路が絶対的に信頼できない状態は、まさにサーバー間通信が持つネットワークの問題と同じだと感じると思います。

この問題に対して現在ネットワークで使われているのが TLS/SSL 通信です。

HTTPS などの TLS/SSL 通信の場合は、サーバの証明書を通してサーバとクライアントのお互いの秘密鍵・公開鍵暗号から作成された共通鍵を使って、途中で「傍受ぼうじゅ」されたり「改ざん」されることを防いでいます。

しかし、残念なことに復号された内容そのものが「正しいか」まではわかりません。https://〜 で始まるからといって安心できるサイトではないのと同じです。（秘密鍵・公開鍵暗号の概要に関しては、本記事上部にある「ハッシュ関数の基本と特徴」を参照ください）

ここで、著者が発行したデータのハッシュ値も別ルートで送れば「復号された内容が正しいこと」を検知できそうです。しかし、どの通信ルートも信用できないため、そのハッシュ値すら正しいか確信が持てません。

同じインターネットのルートでなく、電話網、トークンキーやスニーカーネットワークといった別の媒体のルートを介して確認することを「２要素・・認証」と呼んだりしますが、肝心の電話会社やトークンキー開発会社も運び屋も信用できない状態です。

話した内容がマスメディアを通すと違っていたり、出版物が勝手に書き換えられたり、決算報告で大丈夫と思っていた銀行や企業が突然なくなったり、ホームセキュリティ会社の社員が隠しカメラを設置していたり、脅されているのか血迷ったのか公文書を改ざんしたりする政治家がいる世の中だと、なおさら確信が持てないかもしれません。

そう考えると、意外にリアルな話だと思います。

パスワード付き ZIP が、なぜか共通鍵暗号として全盛だった時代、メールを送ったら届いたか電話で確認するのが流行りました。

ちょうどその頃、プライバシーマークを取得するため「添付ファイルはパスワード付き ZIP でメールに添付して送り、パスワードは次のメールで同じアドレスに送る」のが企業で流行りました。今で言う失敗した「２段階・・認証」の走りです。

しかし、プライバシーマークに限らず ISO や JIS などもそうですが、規格の認証団体は以下のように要件（チェック事項）は定義するものの具体的な実装方法については言及しません。

「個人情報を含む添付ファイルを取扱う際に、セキュリティ対策（データの暗号化、パスワード設定など）の措置を講じること」（第23条）

そして、プライバシーマーク取得の要件を網羅するため昔の企業が独自解釈で取った手法が、パスワード付き ZIP + 別メールであり、「措置を講じている」としたのです。

この時代から「クライアントが本当に欲しかったもの」系の「嘘は言ってないし、要件は網羅しているよね」と、肩書きや体裁を優先しようとした過去の悪しき習慣の 1 つとも言えます。

もちろん、そんなのはダメちんなので、現在は公開鍵暗号と、ちゃんと・・・・した共通鍵暗号を組み合わせた方法が主流になりつつあります。

また、公開鍵は公開鍵基盤を通して安全に取得できるようになりました。つまり、取得した公開鍵を公開鍵基盤に問い合わせて正しい公開鍵であるか確認できるのです。

しかし「某国の、国が管理している公開鍵基盤」と言われて、本当にそれが「正しい公開鍵」であると確信が持てるのでしょうか。

その認証局、信用できますか？

ここで、先の「ビザンチン将軍問題／二人の将軍問題」がチラついてきます。

現在の SSL/TLS 通信は、認証局を銀行や政府のように「信用するしかない」という状態で動いています。つまり、証明書（公開鍵が正しいものであるかの証明書）を発行する組織や企業を信用するしかないのです。

もし、その組織や企業の担当者が洗脳されたり、幹部が敵対国と手を組んでいた場合、偽の公開鍵の証明書を発行する可能性はゼロではないのです。これは、某北の挑戦的な国の公開鍵基盤を某北の挑発的な国が使いたがらないように、お互いの公開鍵基盤を信用していないのと同じです。

世界の海底ケーブルですら、「どの国にケーブルが引き上げられるか」で揉めるのです。

「別にケーブルの中を通るデータが暗号化されてるんだったら、途中で見られてもいいじゃん」と言うわけには行かないのです。役人ですら、パスワード付き ZIP のパスワードを FAX で送ったり、http と https の違いや CC と BCC の違いを知らなかったり確認しないでフォームに大事な情報を入れちゃうようなご時世ですから。

つまり、「A から B へ重要な機密データを伝えたい」という時に、中間に位置する人がそもそも微妙、ということです。

このように「二人の将軍問題」はネットワークの問題だけでなく、中間に位置するものを信用できない状況で起きる現代の問題でもあるのです。

この「二人の将軍問題」を道徳でなく仕組みで解決できるかもしれないというのが話題のブロック・チェーンです。なんと「賄賂などの小銭で寝返る小悪党を味方にしちゃえばいいんじゃね？」という逆転の発想です。

ブロック・チェーンの概要

ブロック・チェーンは「分散型データベース」の一種です。「分散型」と言われるので P2P 型と思われるかもしれませんが、若干違います。

どちらかと言うと git（分散型バージョン管理システム）における、「リポジトリの関係性」（レジストリとの同期など）、リポジトリ管理の仕組みに近いものです。

ここでいう「リポジトリ」とは、データと変更履歴がストックされているディレクトリを言います。そして、ファイル・サーバーのようにローカル外でリポジトリを総括している先を「レジストリ」と言います。GitHub、GitLab、Gitee などはレジストリです。

さて、git の場合、メインとなるリポジトリがレジストリにあり、ユーザーはレジストリからローカルにリポジトリをクローン（コピー）して利用します。業界が違うので用語も異なりますが、DB のマスタを同期して利用するようなものです。

ユーザーがデータに変更を行いたい場合は、ローカルのリポジトリを編集し、その変更をメインのリポジトリにマージ（変更データを反映）します。

そして他のユーザーは、メインのリポジトリに変更があると、同期を行うことで変更に追随します。DB のマスターを更新するイメージに近いのがお分かりでしょうか。

実はブロック・チェーンも DB を管理するメインのマシンがあり、データの登録は「リクエスト → 確認 → マージ（反映）」という手続きを経て、そのメインのマシンが行います。そして同じブロック・チェーンの DB を持つマシンは、メインの変更をローカルに同期します。

「えー。じゃぁメインのマシンが落ちたらどうするの？」と思うかもしれません。

ですよねー。

しかし、git を使う一番のメリットは「同じデータが他の環境にもある」という点です。

つまり、メインとなるマシンが飛んでもリカバリできるという、「環境自体がバックアップになっている」という点も大きいと思われます。DB の場合は「運用でカバー」となるのですが、git やブロックチェーンの場合は運用が仕組みとして組み込まれています。

ブロックチェーンの場合は、それに加え「メインとなるマシンを変更する」というのが仕組みとして組み込まれています。

git やブロックチェーンの問題は速度です。

git の仕組みは「変更のリクエスト → 確認 → マージ（反映）→ 同期」といった手続きが必要なため、リアルタイムにデータが変更されるような環境には適しません。「git リポジトリを同期して DB として使う」と言われると、更新速度に懸念が出るのと同じです。

そして、ブロックチェーンも同じです。

DB への書き込み速度を求める場合は、ブロックチェーンなんかより、従来の DB や、身内だけで構成されたブロックチェーン（プライベート・ブロックチェーン）を使う方がいいのです。

ブロックチェーンを使う唯一のメリットは「堅牢な台帳が欲しい」というケースです。RDB のように、データをこねくり回したり、データの変更（列の値の変更）が重要なものには適しません。

ブロックチェーンの総選挙

ブロック・チェーンにも結局「メインのマシン」があり、メインのマシンに登録し、その他のフォロワーが同期すると述べました。問題は、そのメインのマシンがトラブルでダウンした場合です。

実は、このメインのマシンは「リーダー」と呼ばれ、選挙制（フォロワーの多数決）で適宜決まります。

現在のリーダーのマシン（ノード）が落ちると、即座に選挙が始まり次のリーダーを決定し、他のノードはフォロー先を変えるのです。

この時に使われる選挙アルゴリズムの 1 つが「Raft」と呼ばれるものです。ブロックチェーンの種類によって選挙アルゴリズムは異なりますが、raft は etcd などの分散キー・バリュー・ストア型の DB でも使われているアルゴリズムです。ちなみに etcd は Kubernetes などのクラスター型のアプリケーションでも利用されています。

Raft | Raft 公式 @ GitHub
Raft | EN @ Wikipedia
etcd/raft | etcd.io @ GitHub

後述するブロックチェーンの「51% 問題」は、この「多数決」にあります。

つまり、フォロワーの過半数が結束すれば次のリーダーを意図的に決定することができるのです。そのため、Raft アルゴリズムだけでは「ビザンチン将軍問題」は解決できません。意図的に指定された特定のリーダーが、改竄かいざんデータを挿入する可能性もあるためです。

台帳とは

ブロック・チェーンを知る上で重要な用語の 1 つに「台帳」があります。

ブロック・チェーンは「分散管理台帳」とも呼ばれるのですが、経理や経理系のシステムに携わったことのある人でないと、「台帳」という単語は馴染みがないかもしれません。実は、「台帳」という単語を理解しないとピンとこないこともあります。

先にも触れましたが、「台帳は追記しかできないデータ・ベース（以下 DB）」です。一度書き込んだら変更できません。

そして、変更をしたい場合はデータの書き換えでなく「変更の追加」をするということです。つまり、「7」という値を「5」に修正したい場合は、「-2」という変更を追加して調整します。経理の台帳で言う「赤伝」（マイナス調整をするための伝票）です。

この仕組みは身近なところで見ることができます。銀行の通帳や国民基本台帳です。貯金額や住所変更は「書き換え」でなく「追記」することで更新します。

ビットコインなどの仮想通貨（暗号通貨）も、DB の最初に作成したコインを登録しておき、それをプラス、マイナスしているのです。

実は、変更のみ追加していく仕組みは git も似ています。

しかし git はデータを書き換えることが技術的にできるのに対し、ブロック・チェーンは仕組み上できません。いや、厳密にはできるのですが限りなく不可能です。これが分散台帳とも呼ばれる所以ゆえんです（なぜ変えられないかは後述します）。

git に慣れている人であれば、ブロック・チェーンは「絶対的に過去のデータを変更できない git のようなもの」と考えても差し支えないかもしれません。

しかし、git と決定的に違うのは「メインとなるマシンは投票で決まり、適宜変わる」という点です。GitHub が落ちたらフォーク先が選挙で GitLab にするか Gitea にするか決めて、フォーク元を一斉に変更するようなイメージです。

また、後述する「何を、どのように登録するか」も、投票や他のマシンの検証により決まります。そして投票で決まった内容が反映されていた場合のみ、他のマシンもローカルを同期します。

つまり、メインとなるノードは「投票で決まったデータの登録をするだけ」という役回りになります。

そのため、メインとなるマシンが落ちても、自動的に他のマシンが投票により決まるため、1 台でも DB を持つマシンがあれば「サービスが消えることがないデータ」を提供できることになります。

となると「どのようにデータを管理するのか」が気になるところですが、ここでハッシュ関数が出てきます。

ブロック・チェーンの構造

ブロック・チェーンの基本構造は割と単純で、「１つのデータが、前のデータのハッシュ値も持つ」というものです。

そして、後述する「プルーフ・オブ・ワーク」（もしくは「プルーフ・オブ・ステーク」）と言う概念とセットとなったものを「ブロック・チェーン」と言います。

ブロック・チェーンは「サトシ・ナカモト」なる日本人と思わしき謎の人物が提唱したと言うのは聞いたことがあると思います。

実際にそうなのですが、厳密には「従来からある 2 つの考え方を組み合わせたものから発想を得たもの」と言えます。以下がおそらくその 2 つです。

マークルの木（ハッシュ木）
マークルのパズル

ここで、先のハッシュ関数の基礎知識で「塩（salt）は後から足す」の話しに出てきたヒーロー・ロボットのような名前の「マークル・ダンガード」を思い出してください。

実は、この「マークル」はラルフ・マークル氏のマークルなのですが、個人的に「もっと評価されるべき」的な人物だと思います。（いや、業界では超有名人なので一般に認知されるべき人と言うか）

どうもマークル氏は、日本で言えば南部陽一郎さんのような、アイデアをポンポンと投げては他の人に影響させるタイプの人だったらしく、公開鍵暗号の基礎となるアイデアを作ったり、暗号学的ハッシュの元となるマークル・ダンガードを発明したり、ファインマン氏が予言＆提唱した量子コンピュータを「物質を原子レベルの大きさで制御しデバイスとして使う」という「コンピューターと分子ナノテクノロジーの融合のパイオニア」と呼ばれたかと思えば「人体冷凍保存の人」と言われたり。まぁ、それは変な人です。存命の方なので Youtube などでググれば色々な講演が聞けます。

さて、「１つのデータが、前のデータのハッシュ値も持つ」と言いましたが、この構造の概念自体は git のコミットハッシュなど、ブロックチェーン以前から存在しており、そのベースとなるのが「ハッシュ木」です。

そして、「プルーフ・オブ・ワーク」の元になるのが「マークルのパズル」です。

木と言うよりチェーン

ハッシュ木の場合は、木を逆にしたような構造で「子」となるブロックのハッシュを「親」が持つと言うものです。この構造は、複数のファイルや、分割したデータから 1 つのハッシュ値を作成する場合などに使われます。

ブロック・チェーンは、それをシンプルに 1 本にした感じのものです。

各ブロックには「データ」と「ハッシュ値」があり、ハッシュ値は 1 つ前のブロックのデータとハッシュ値をハッシュ化したものです。

このハッシュの値がブロックとブロックのつなぎとなりチェーンになっているため、ブロック・チェーンと呼ばれます。チェーンに見えますでしょうか。

実は、ブロック・チェーンは「データ」に工夫がされており、保存したいデータのフィールドと nonce と呼ばれるフィールドがあります。

`nonce` って、なんっスか？

nonce（ナンスもしくはノンス）とは「1 度だけ使われる数値」で、"Number used once" とも言われますが略語ではありません。

nonce は、nine（9）や none（なし）の語源にもなった nones から来ています。nones は、ローマ暦が 8 をベースにしていた時代に、都合が悪い時に使った謎の調整値のようなものです。今でいう閏年や閏秒みたいなものでしょうか。

そこから 8 の次の 9（nine）や、存在しないもの（none）に変化しました。転じて「一時的に調整のために使われるもの」を nonce と言うようになりました。〜 for the nonce のようにも使われ、日本語で言えば「とりま〜とりあえず、なんとか」みたいな時に使う感じでしょうか。

ブロックチェーンでは、nonce は 1 つのブロックと次のブロックをつなげるためだけに 1 度だけ算出される数値です。

Qiita ユーザには下手な概念図で示すより、データで見た方がピンとくるかもしれません。

ブロック・チェーンのデータを JSON 形式で簡略表現すると以下のようになります。hash data nonce の１セットを１ブロックとします。

[
    {
        "hash": "<hash1>",
        "data": "<data1>",
        "nonce": "<nonce1>"
    },
    {
        "hash": "<hash2>",
        "data": "<data2>",
        "nonce": "<nonce2>"
    },
    ...
]

上記の hash、data、nonce の 3 つのキーの内容は以下の通り。

hash キーの値は、前のデータの hash と data と nonce の値をつなげてハッシュしたものです。（<hash2> = hash('sha256', <hash1> + <data1> + <nonce1>);)
data キーの値は「何かしらのデータ」で平文でも暗号文でも構いません。プログラムのスクリプトであっても構いません。なんなら WebAssembly の WASM バイナリだっていいのです。
"nonce" キーですが、これがブロック・チェーンのキモ・・です。

"nonce" は「キー・ストレッチング」の一種です。（「ストレッチング」については、文頭の「塩だけでなく胡椒も足そう」のコメント欄をご覧ください）

つまり "nonce" は、クラッキング（悪いこと目的の操作）に対する「面倒くささ」を加えるための、ひと手間です。この nonce の値を算出することを「マイニング」と呼んでいます。

マイニング（発掘）と呼ぶのは、この nonce の値を最初に見つけ、承認を得られた人は報酬がもらえるからです。ブロック・チェーンがビットコインの場合は、ビットコインがもらえます。

この nonce 値を見つけることが現金につながるだけでなく、みんなのマイニング作業や承認作業によって「データのハッシュ値が正確であるか」を複数人で確認しあっていることになるため、データが堅牢になって行きます。

^{🐒 たまにマイニングを仮想通貨（暗号通貨）そのものを発掘するような意味とも思える記述を見かけますが、違います。}

^{「金を発掘したら俺のもの」的な宣伝が多いのでわかりづらいのですが、どちらかと言うと「レアメタルを発掘したら報酬でお金がもらえる」イメージが近いと思います。ビットコインの場合は「nonce 値」がレアメタルで、「ビットコイン」が報酬のお金です。}
^{仮想通貨自体は１コインごとに、コインの秘密鍵とコインの ID となるハッシュ値がセットになったようなデータで、各コインは 0〜1 の float 値を持っており分割可能です。ビットコインの場合は、1.00000000 まで分割可能です。このコインは、一般的に ICO と呼ばれるステップで作成（発行）され、ブロックチェーンの初期値として登録されます。そこから、ユーザーが購入もしくはもらうことでコインの移動が始まります。}
^{受け取ったコインは、ユーザーごとに作成される秘密鍵とフォルダをセットにした「ウォレット」と呼ばれる先に保存されます。この時、ユーザー間のウォレットでコインが移動したときの取り引き内容が「ノード」と呼ばれる先の DB にブロック・チェーン形式で記録され、他のノードと同期されます。}
^{これによりコイン・データがコピーされても、ブロックチェーンに記録されている最終ウォレットの鍵と異なるウォレットの場合は無効になります。ウォレットの秘密鍵を持つ者でなければ次のウォレットに移動できないため、秘密鍵を無くしてしまうと、コインを使うどころか、自分のものであることを証明することも、現金化するために換金所のウォレットへも移動できなくなります。逆に言えば、ウォレットの秘密鍵が盗まれてしまえば、移動できてしまうということでもあります。通帳と印鑑や、キャッシュカードと暗証番号が盗まれるようなものです。}

^ノード
^{ブロックチェーンにおける「ノード」はブロックチェーンのピアのうち「DB の管理をしているピア」です。コイン取引所やメンテナやマイナー（マイニングをする人）などが「ノード」に該当します。各々のノードの DB は同期されており、これがブロック・チェーンを「分散台帳」とも呼ぶゆえん・・・です。「ノード」はネットワークの常時接続やディスク容量が必要といったデメリットもありますが、「ノード」になるメリットはブロックチェーン追加時に報酬のためのコインを作成（発行）することができる点と DB 追加の手数料がもらえる点です。そのため、初期の頃は、ノードとマイナー（マイニング）を兼任するサーバーも多く、これが「マイニング＝コインの発掘」というイメージを産んだ理由でもあります。}

^{いずれにしても、ブロック・チェーンは DB の１種であると考えて差し支えないと思います。そのため、ブロック・チェーンの仕組みは仮想通貨／暗号通貨でなくても活用できます。}

^{ビットコインのメールと論文 by サトシ・ナカモト}

^{ビットコイン論文からさぐるブロックチェーンのヒント @ オブジェクトの広場}

ブロック・チェーンは "nonce" センスなゲーム

ブロック・チェーンにおける nonce は、一言で言うと「ハッシュ値の衝突を探すゲームで、最初に見つかった値」です。

このゲームとは「現在の data と hash に、nonce を加えてハッシュ化すると、最初の n 桁が 0（ゼロ）になる nonce の値を探す」といったものです。

00の衝突を探す例

// 1 つのブロック・データ
$data = 'something';
$hash = '34902903de8d4fee8e6afe868982f0dd';
$nonce = 'd9'; // <- 見つけた nonce 値

// md5 でハッシュ（$data.$hash.$nonce）
$result=hash(md5, 'something34902903de8d4fee8e6afe868982f0ddd9');

// ゲームの結果確認
echo $result; // -> 00603ea2b0f451d9531b6caeb0e96afb
// result の最初の 2 桁が 0 （ゼロ）なのでクリア！

その桁数や 0（ゼロ）の値などはブロックチェーンによってルールは異なりますが、いずれも nonce を加えてハッシュ化した時に出る値に対するルールです。

nonce を探すイメージを Bash で書いてみました。

bashでマイニングする（nonceを探す）例

#!/bin/bash

# RULE
VALUE_HEAD='0000'
LEN_HEAD=${#VALUE_HEAD}

# Function
function dechex() {
    printf '%x' $1
}

function isValidNonce() {
    [ "${1:0:$LEN_HEAD}" = "${VALUE_HEAD}" ]
    return $?
}

function hash() {
    algo=$1
    value=$2
    echo $(echo -n $value | openssl $algo | awk '{print $2}')
}

# Data
data='something'
hash='34902903de8d4fee8e6afe868982f0dd'
nonce=''

# Mining/Search nonce
counter=0
while true
do
    nonce=$(dechex $counter)
    string_to_hash="${data}${hash}${nonce}"
    hash_temp=$(hash 'md5' $string_to_hash)
    isValidNonce $hash_temp && {
        break
    }
    counter=$((counter+1))
done

echo "Nonce found: ${nonce}"

オンラインで動作をみる @ paiza.IO

しかし、ブロックチェーンは「一度、生でブロックチェーンを見たら分かる」と言われるくらいなので、全体の流れをプログラムで見た方がピンとくるかもしれません。

PHP で簡単に書いてみました。（実際に触れるようにもしているので、そんなに根詰めて読む必要はありません。この記事は、ざっと流れがわかればおkで、むしろ「用語に見慣れるために読む」程度の意気込みでお読みください）

既存のブロック・チェーンのデータ

// ２つ前のブロック・データ
$block_chain[] = [
    'data'  => 'sample1',
    'hash'  => 'a4626f9d3e6802aebbff46697248e0b9',
    'nonce' => 'xxxxxx',
];
// １つ前のブロック・データ（Latest）
$block_chain[] = [
    'data'  => 'sample2',
    'hash'  => '3152851bf5419247cf948e871b0adfe8',
    'nonce' => '32648',
];

Nonceのルール

// 最初の４文字が 0 である
define('VALUE_HEAD', '0000');
define('LEN_HEAD', strlen(VALUE_HEAD));

/* 検証用の関数 */
function isValidNonce(string $nonce): bool
{
    // ルール：$nonce の頭 n 文字が VALUE_HEAD と同じ( n = LEN_HEAD )
    return (substr($nonce, 0, LEN_HEAD) === VALUE_HEAD);
}

function isValidHashInLatestBlock(array $block_chain): bool
{
    // 現在のブロックの長さ
    $len_block_chain = count($block_chain);

    // ２つ前のブロックのデータ取得
    $key_2block_ago = $len_block_chain - 2;

    $data_2block_ago  = $block_chain[$key_2block_ago]['data'];
    $hash_2block_ago  = $block_chain[$key_2block_ago]['hash'];
    $nonce_2block_ago = $block_chain[$key_2block_ago]['nonce'];

    // 期待するハッシュ値の算出
    $hash_previous_expect = hash('md5', $data_2block_ago. $hash_2block_ago . $nonce_2block_ago);

    // １つ前のブロックのハッシュ値取得
    $key_block_previous   = $len_block_chain - 1;
    $hash_previous_actual = $block_chain[$key_block_previous]['hash'];

    // １つ目のブロックのハッシュ値の検証
    return ($hash_previous_expect === $hash_previous_actual);
}

function getBlockLatest(array $block_chain):array
{
    $len_block_chain = count($block_chain)-1;
    return $block_chain[$len_block_chain];
}

ブロックチェーンにデータを追加したい人の作業

/* １つ前のブロックの検証 */
if(! isValidHashInLatestBlock($block_chain)){
    echo 'Error: Not a valid hash value. Block-chain broken.' . PHP_EOL;
    exit(1);
}

/* 新規ブロックのデータ作成 */
// 追加したいデータ
$data_current = 'sample3';
// ブロックのハッシュ値を計算（１つ前のブロックより）
$block_previous = getBlockLatest($block_chain);
$hash_current   = hash('md5', $block_previous['data'] . $block_previous['hash'] . $block_previous['nonce']);
$block_current  = [
    'data' => $data_current,
    'hash' => $hash_current,
];
echo 'Request to add to the block-chain.' . PHP_EOL;
echo '  Data:' . $data_current . PHP_EOL;
echo '  Hash:' . $hash_current . PHP_EOL;

マイナー（マイニングする人）の作業

/* １つ前のブロックの検証 */
if(! isValidHashInLatestBlock($block_chain)){
    echo 'Error: Not a valid hash value. Block-chain broken.' . PHP_EOL;
    exit(1);
}

$data_current  = $block_current['data'];
$hash_current  = $block_current['hash'];
$nonce_current = '';
// Nonce 探索
$i = 0;
while( true ){
    $nonce_current = dechex($i);
    $hash_temp = hash('md5', $data_current . $hash_current . $nonce_current);
    if(isValidNonce($hash_temp)){
        echo 'Nonce found: ' . $hash_temp . PHP_EOL;
        break;
    }
    $i++;
}

/* マイニングの結果（これを検証依頼する） */
echo 'Block Data to add:' . PHP_EOL;
echo '  Data: ' . $data_current . PHP_EOL;
echo '  Hash: ' . $hash_current . PHP_EOL;
echo '  Nonce: ' . $nonce_current . PHP_EOL;

ブロック・チェーンに追加する人の検証作業

/* １つ前のブロックの検証 */
if(! isValidHashInLatestBlock($block_chain)){
    echo 'Error: Not a valid hash value. Block-chain broken.' . PHP_EOL;
    exit(1);
}

// 発見された nonce の検証
$hash_verify = hash('md5', $data_current . $hash_current . $nonce_current);

echo 'Hash result: ' . $hash_verify . PHP_EOL;
if(! isValidNonce($hash_verify)){
    echo '  Error: Nonce not valid.' . PHP_EOL;
    exit(1);
};

// ブロック・チェーンに追加
$block_chain[] = [
    'data'  => $data_current,
    'hash'  => $hash_current,
    'nonce' => $nonce_current,
];
echo '  Success: New data added to block-chain.' . PHP_EOL;

// ブロック・チェーンの内容表示
echo 'Current Block-Chain:' . PHP_EOL;
print_r($block_chain);

オンラインで動作をみる @ paiza.IO

上記で重要なのが、マイナー（マイニングする人）の処理にある「Nonce 探索」の while ループの箇所と、データを追加する人の処理にある「発見された nonce の検証」のハッシュ値の計算箇所です。

マイニングの while ループの箇所の箇所ですが、一部のマッチが true になるのか、全文マッチが true になるか以外はマッチ対象が違うだけでハッシュ値の衝突を探す手法そのままです。つまり、総当たりで根性で探しているのです。

実際には文字列の比較でなく、FF000... で and 処理（ビットマスク）した方が速いなどありますが概念的に、こういうことです。😳

^{🐒 実際の「ブロック・チェーン」のデータは高速化なども配慮してもっと複雑です。しかし基本概念は同じです。}

^{また、ブロック・チェーンではデータの塊かたまりを「ブロック」と呼ぶのですが、ネットワークの「パケット」と「フレーム」のように、ブロックと呼ばれる区分けがレベル（レイヤー）によって違います。ここでは仕組みがわかりやすいように「登録したい１つのデータ」を「ブロック」と呼びます。参考として、ビットコインなどは「n 分間の取引データ」を１ブロックと時間単位で区切っています（現在は n=10）。そして登録される個々のデータを「トランザクション」と呼んでいます。}

どのような nonce の探し方であっても、平均して特定の時間前後かかるように 0（ゼロ）の長さのルールが自動調整されます。ビットコインの場合は、およそ 10 分前後になるように調整されます。

反面、探索された nonce の値のチェック（nonce を使ってハッシュ値を出して頭 n 桁が 0 であるかの確認）は、一瞬で終わってしまいます。

ここで大事なのが、「nonce を探すのは大変だ（時間がかかる）がハッシュ関数で確認することは一瞬」ということです。

プルーフ・オブ・ワーク（仕事の証明）

ブロック・チェーンの重要な基本ルールに「現在一番長いチェーンを『正』とする」があります。

これはリーダー（DB 登録担当）のノードがダウンした時に次のリーダーを決める際に、一番長いチェーンを持っている（データ量の多い）ノードから選抜するということです。

つまり、リーダーと同期していなかった場合、せっかく計算しているのに短い方（古い方）のブロックチェーンを使っていることになり、nonce を見つけても無効になるということです。

また、自分より早く「nonce を見つけた！」という人がいた場合、計算を続けても電気や時間のリソース（👌）が無駄になってしまいます。nonce が none になってしまいますのん。

そこでマイナー（マイニングする人）は、本当に見つけたのかを確認する作業を行い、正しければ早々にブロックチェーンを更新して、次の登録待ちデータのマイニングを始めるのです。

この仕組みにより、ブロック・チェーンの途中にあるデータを改ざんしようとした場合、大変なコストが発生します。

改ざんしたブロックより後のブロックのハッシュ値の計算だけでなく nonce の値まですべて再計算してリリースしないといけないからです。それだけでなく、世界中のマシンに散らばったブロック・チェーンのデータにも不正アクセスして書き換える必要もあります。

しかし、改ざんして再計算したり、他のマシンをハッキングしてデータをクラックしている間にも、よほど過疎っているブロックチェーンでない限りデータはどんどん長くなり更新されていきます。改ざんさせる暇を与えづらい状況が作られるのです。

ビットコインの場合は、ウォレット間の移動がある（取引がある）たびに 10 分おきに長くなって行くので、とうてい間に合わないのがわかると思います。

さらに、2020 年 07 月の現在のビットコインのブロックチェーンの長さは約 270 GB です。これを改ざんするには、10 分以内に「改ざん箇所以降の全て」の nonce 値を計算する必要があります。しかし、肝心の nonce 探索は 1 つ見つけるまでに 10 分前後になるように自動調整されているため、かなり難しいことが実感できると思います。

つまり「データを改ざんして小銭を稼ぐよりはマイニングした方が稼げる」ということです。

そして、当然これらの処理は自動で行われます。つまり、スパムメール／フィッシング／詐欺商品／ゴミ記事の広告収入など、単純作業を自動化して「数を打って薄利多売で稼ぐ」という昔ながらの手法を使う人にとっては「楽して稼げる」手法の 1 つになります。

しかも、「他人のマイニング結果の粗探し」が結果としてブロック・チェーンの正当性（データのハッシュ値が同じであること）を保証することになります。そのため、「ホワイト」しかも「ウィン・ウィン」となります。

犯罪心理学では「金づるとなるサービスには悪さはしない」というのがあります。大半の寄生虫がホストを殺さないのと同じ行動です。

手元にある大量のハッシュ値がただのゴミの数値になるような「ブロックチェーン自体がダメになる悪さはしない」という、中小規模の悪党の犯罪心理学を逆手に応用した、敵を味方に付ける有効な（面白い）概念なのです。

もちろん、国家レベルの資金がある大規模な悪党が、相手を（別のコインを）潰すために鬼のようなマシンを大量に用意できれば、以下の攻撃でブロックチェーンを改ざんデータ入りで更新させることはできます。

改ざん後、残りのすべてを再計算し、現在のブロック・チェーンより少しだけ長いチェーンを作成しておく。
ノードの過半数が結託して、次のリーダーを誰にするか合意しておき、投票を手動で行えるようにアプリをいじる。
次のリーダー予定のノードは、上記の改竄ブロックチェーンを持ってスタンバイしておく。
現在のリーダーに DoS 攻撃をしてノードをダウンさせる。
投票が始まったら、予定されていたノードにノードの過半数が投票する。
リーダーが（悪い方へ）変わり、ブロックチェーンの長さも違う（長い）ので、他のノードは同期を始める。

当然 nonce のマイニングでなく過去のデータの検証だけを行う人も出てきます。しかし、異議を唱えても、マイノリティであるため、過半数の力には負けてしまいます。このような攻撃を「51% 攻撃」と呼びます。（詳しくは後述します）

しかし、利用者が多ければ多いほど、また多種多様な人がいればいるほど、この攻撃はしづらくなります。

このように、ブロック・チェーンは「複数人でチェックしあい、チェックしてもらったら早い者勝ちで報酬を与える」「チェーンの長さがセキュリティにつながる」「利用者が多ければ多いほど堅牢になる」「DB のバックアップ（コピー）をしてくれる人にはインセンティブ報酬を与える」という仕組みなのです。

この、データのハッシュ値を確認し nonce の値を探す、それを他者が粗探し（検証）をし、問題なければ各々のチェーンに追加する。これを「プルーフ・オブ・ワーク」（「仕事の証明」もしくは「仕事による証明」）と呼びます。

`nonce` のゲームとマークルのパズル

キーストレッチングしかり、nonce 探索しかり、現在のセキュリティのベースにあるのが「悪さをしたい人に手間をかけさせる」ことです。

例えば、暗号化された 1 データをクラッキングして復号するのに 1 ヶ月かかるとして、どんな小さなデータも暗号化されていた場合、「クラッキングする側はやってられない」というような状況を作るのが基本です。Chrome ブラウザなどがデフォルトで https にするのも同じ理由です。

さて、ここで「マークルのパズル」について説明したいと思います。

「マークルのパズル」とは、公開鍵暗号や暗号学的ハッシュの種をまいていた例のマークル氏が考えた「パズルを使った『二人の将軍問題』の 1 つの解」です。Wikipedia によると以下のような説明がされています。

マークルのパズル（英: Merkle's Puzzles）とは、ラルフ・マークルが 1974 年に考案した初期の公開鍵暗号システムであり、1978 年に発表された。事前に秘密を共有していなくとも、メッセージを交換することで秘密を共有できる方式である。

（マークルのパズル @ Wikipedia）

ここで注目して欲しいのが「事前に秘密を共有していなくとも、メッセージを交換することで秘密を共有できる方式」の一文です。

これは「二人だけの秘密」と言う点で、先の「公開鍵・秘密鍵暗号」にも言えることだし、「二人の将軍問題」にも言える内容だと思います。

このパズルのシチュエーションですが、「離れ離れのアリスとボブが、メッセンジャーとなるチャーリーにバレずに秘密のメッセージを送ることができるか」と言う状況です。もぅ、まんまですね。

そこでマークルは、パズルを使った方法で解決しようとします。

まず、ボブは、そこそこ難しいが適度な時間（例えば n 日）で解けるパズルをたくさん用意してアリスに送ります。どのパズルも、パズルを解くと、一意の「暗号鍵」と「識別 ID」がわかるようになっています。

ある日、ボブに秘密のメッセージを送りたくなったアリスは、ボブからもらった、たくさんのパズルから 1 つランダムにピックアップしてパズルを解きます。

そして、そこから得られた暗号鍵でメッセージを暗号化して、識別 ID と一緒にメッセンジャーのチャーリーに託します。

チャーリーはこっそりと盗聴したいと思うも、どのパズルが使われたか分かりません。

そこでチャーリーは、彼が唯一わかっている情報である「識別 ID」がヒットするまでボブのパズルを 1 つ 1 つ解いていかないと盗聴（復号）できません。

問題はパズルを解くのに 1 つあたり n 日かかることと、ボブが送りつけてたパズルが図書室が埋まるくらいの数である、しかも定期的に新規パズルが送られてくるため、「実質的に無理」と言う状況がおきます。

もちろん王様クラスの命令で、うん千人が同時にパズルを解くような👌リソースを持っていれば話しは別です。しかし、パンピーのボブとアリスがちちくり合うだけのメッセージにそのようなコストはかけてもらえません。

どうでしょう。ブロックチェーンの nonce 検索も「マークルのパズル」に近い考え方だ、とわかると思います。

「実現不可能なレベルで手間をかけさせる」。これが、現在のセキュリティの根本的な手法です。

ブロックチェーンのセキュリティ

ちなみに、巷で何度か「暗号通貨（仮想通貨）が盗まれた」という事件が発生していますが、これはブロックチェーンの仕組みが崩れたわけではありません。

単純に、パソコンがクラッキングされ、暗号通貨用の秘密鍵が盗まれてしまい、別の口座に移されてしまったという、クレジットカードや銀行口座のそれ・・と同じで、個人や取引所のセキュリティ管理上の問題による事件です。「ほらな」と言いたいメディアが仕組みを把握せずに印象操作をしているだけです。

この 10 年で、銀行のトラブルがあったことは何回あったか考えてみてください。個々の取引所のメンテナンスや不祥事などを除き、ブロックチェーン・ベースのコインの取引自体はトラブルで止まったことは 1 度もないのです。

51%攻撃（数の暴力）

おそらくブロックチェーンのセキュリティでシステム的に一番有名な攻撃が 51% 攻撃と呼ばれるものです。一言で言うと「多様性に欠けた際の、多数決による意思決定の情報操作」です。

ブロックチェーンは P2P 型であるため、基本的に主となるサーバーが存在しません。各々がピア、つまりサーバーでありクライアントであるからです。

とはいえ、P2P ネットワーク内で、代表でデータを追加する「リーダー・ノード」がいます。このリーダーは、リーダーに追随するフォロワー（ブロックチェーンを同期する側のノード）の選挙の多数決で決まります。また、データを追加するかの意思決定もフォロワーの多数決で決めることになります。

「ノード」とは、ピアのうちサービスを提供している状態（サーバー状態）のピアを言います。ここでは、先述したように分散同期された各々のブロックチェーンの DB サーバーのことです。

各ノード（サーバー）には、各々マイナー（マイニングする人）やユーザー（ブロックチェーンにデータを追加したい人、例えば仮想通貨の場合は取引内容を登録したい人）が所属しています。

この時、間違った登録内容であってもノードやマイナーの過半数が「問題ない」と答えると登録されてしまうのです。ここで言う「間違った」と言うのは、ハッシュ値が合わないデータではなく、データそのものを改竄した物を言います。

なぜできるかと言うと、その多数決で決まったリーダーもその仲間だったら追加する権限があるからです。

つまり、現実世界の多数決と同じように、数と資産（処理能力）を持った組織でコントロールすることができてしまうのです。

^{🐒 資本主義と犯罪学の観点からは、残念なことにブロック・チェーンを仮想通貨（暗号通貨）に使うにも昔からある問題が出てきています。}

^{ビットコインの場合、マイニングにかかる時間（nonce が発見されるまでの時間）が自動的に 10 分前後になるようにルール（ゼロの個数）を調整しています。逆に言えば、マシン・パワーを持つ人が常に優位になるということです。}
^{「今からマイニング事業を始めても儲けが少ない」と言われるのは、初期のころからルールにあわせて設備投資していた人と比べ、必要なマシンスペックの費用対効果が薄いからです。そうなると、すでに資本（マシンパワー）を持っている人にしか稼げない土壌ができつつあります。せっかくの「小悪党を味方に付ける」仕組みが崩壊する可能性もあるのです。}
^{また、マイナー（マイニングする人）のバラエティが少ないと、イレギュラー時に全滅する可能性も高くなります。特に上記の 51% 攻撃をさせやすくなってしまいます。}
^{そういった多様性の欠落問題に対して、マイニングの処理を分散させて、資本が少ない（マシン・スペックが低い）人でもマイニングに参加できるような仕組みも出てきました。事件にもなった Coinhive などです。この事件は Winny と同じく「犯罪の温床となりうるから」と検挙された事例で、どちらも無罪とはなったものの、どちらも「賢くない人」が「ズル賢くやろう」と迷惑をかけた・配慮に欠けたことによる弊害で、開発者もしくは技術そのものがトバッチリを受けた事件です。どちらの技術も「分散技術における重要なもの」ではありました。}
^{これらの裁判がアンチ資本主義（資本を持っている人を脅かす考え方）に対する弾圧とまでは言いませんが、少なくとも Winny の件は日本の分散技術が世界から遅れた理由ではあります。}
^{「賢くない人から賢い人にお金が集まる」ことを資本主義の特徴の１つと仮定すると、犯罪における資本主義は「賢くない人からズル賢い人にお金が流れる仕組み」とも言えます。つまり「賢くない手下にマシンを走らせ、ズル賢い元締めに流れる仕組み」が生まれてきます。犯罪組織の王道の仕組みです。つまり、マイニングから得たクリーンな資金が犯罪組織の資産にもなりうるということです。}
^{しかし、これらはブロック・チェーンに限らず、自動的にお金が発生すると必ず起きる問題です。そのため、ブロック・チェーンの仕組みとは分けて考えるべきです。}

さて、DB の改ざんにスポットを当てると、不特定多数で多様性に富んだ組織においては、一見ブロック・チェーンがベストな方法に見えます。

しかし、nonce のように「そもそも時間をかけることでセキュリティを高めている」仕組みである以上、ブロック・チェーンは遅いのでケース・バイ・ケース（適材適所）と言えると思います。

また、ブロック・チェーンが「分散台帳」とも呼ばれるように、DB の分散に関しては、ハッシュ関数とは別の話しなので割愛しますが、以上のようにブロック・チェーンにはハッシュ関数の特徴が存分に活かされているのがわかると思います。

いずれにしても、この性善説（相手を信用する）でなく性悪説（悪党は楽をして稼げる方を選ぶ）を逆手に取った社会的な心理も加味したプルーフ・オブ・ワークの仕組みにより「A → B への（遅いけど）正確なデータの伝達が可能になった」のがプログラマとして面白いなー、と思うところです。

併せて読みたい：「Gitとブロックチェーンの関係」@ Qiita

ブロックチェーンの環境問題について

ブロックチェーンや、後述する NFT について語る場合、必ずと言って良いほど環境問題が取り上げられます。

これは、ブロックチェーンの PoW（プルーフ・オブ・ワーク）の処理において「電気を食いすぎるので環境に悪い」という意見です。

確かにブロックチェーンは、ブルートフォース祭り状態、つまり「nonce の値を探すためだけ・・に、鬼のような for ループを走らせる」ため、そのトータルの消費電力は馬鹿にできません。

ビットコインで言えば、ちょっとした国 2 つぶんくらいの消費量と言われます。そのため、その電気消費量は無視できるものではありません。

しかしこれに関して結論（「ブロックチェーンは環境破壊なのか」という問題の答え）を出すには時期が早く、さまざまな意見があるのですが、筆者の 1 意見を述べたいと思います。

答えを先に言うと「ブロックチェーンの堅牢性は認知されてきているのだから、電気を大量に消費しない方法を考えればいい」ということです。後述するイーサリアムの PoS（プルーフ・オブ・ステーク）などの改良版がそれに当たります。

nonce 探索というゲームのようなものに電気を食うとはいえ、決して意味のない処理や生産性のない処理をしているわけではありません。

本質的に、それは「分散データの改竄防止のための処理」として電気を食っているからです。そして、それから得られるメリットは「中央集権型ではない」ことを維持できることです。

つまり 1 社が倒産したりサービスを止めると、全てがなかった・・・・ことになる中央集権型のサービスと違い、ブロックチェーンは特定の会社だけがサービスを提供しているわけではないため、利用者がいる限り残るということです。

恐れずに言うと、サービスというよりはインターネットに近い「インフラ」なのかもしれません。

逆に、GAFA始め「中央集権型のサービス」の提供側と利用側が消費する電力はどうなのかも考えないといけない、ということです。

ここで、先の「ビザンチン将軍問題」と「マークルのパズル」を思い出してください。つまり、この問題を解決できるのであれば、別に PoW（プルーフ・オブ・ワーク）に固執する必要もないのです。

事実、イーサリアムなどのブロックチェーンは PoS（プルーフ・オブ・ステーク）を改良して消費電力を大幅に減らしています。

`PoW`（プルーフ・オブ・ワーク）と `PoS`（プルーフ・オブ・ステーク）の違い

PoW（プルーフ・オブ・ワーク）と PoS（プルーフ・オブ・ステーク）は、どちらも「nonce の探索」と「ハッシュ値のチェック」をし、その結果を他のノードの多数決で承認・登録する点では同じです。

PoW と PoS の違いは、依頼をする先のアルゴリズム（処理の考え方）にあります。

従来の PoW が「nonce 探索を行うのは誰でもいいから早いもの勝ち」「誰も信用しない」であるのに対し、PoS は「nonce 探索を行うのはランダムに指定されたノード」で「信用という資産（steak）を重視」します。

いささか毒のある言い方ですが、先の「金づるとなるサービスを害さない」心理や「寄生虫はホストを殺さない」という考えをさらに発展させ、「資産を多く持っている方が失った際のリスクが多いので、その資産に対して真面目である」という考え方にシフトしています。

どういうことか。

PoS の S は steak のことで「資産」「利害関係」「差し出す」「提供する」といった意味を持ちます。

ここで言う「資産」とは、コインの「保有量」と、それまでの取引量による「信用度」です。一言で言えば「実績」です。

PoW は誰でもマイニング（nonce 探索）に参加でき「早い者勝ち」だったのに対し、PoS の場合はマイニングを行うノードは「ランダムに、ご指名」制です。

とは言え、どのノードでもいいわけではありません。依頼先のノードの「実績」が低かった場合は、さらに他のノードにも探索依頼します。

つまり、他のノードと折半するぶんインセンティブ報酬が低くなります。逆に言えば、コツコツと真面目に処理していれば信用度もあがり、インセンティブも多くなります。

これにより、早い者勝ちで無駄の多かった nonce 探索の消費電力が劇的に少なくなります。また、ランダムであるため、マシン・スペックの低かったノードにもチャンスが回ってきます。

この概念を、さらに改良して取り入れようとしているのが「イーサリアム」などの仮想通貨（暗号通貨）です。

さて、消費電力の話しですが、おそらく近い将来「そもそも」の nonce 探索を使わない方法も出てくると思います。例えば先の「イーサリアム」は PoS において実証実験を行っています。

そのため、ブロックチェーンの技術と、暗号資産（ビットコインやイーサリアムのコイン）は別のものとして考えることが大事です。

その上で「環境問題」を見ると、暗号資産としての相場を煽るために問題にしている人が裏にいるように思えてなりません。

NFTとは = IPFS + ブロックチェーン？

さて、ここまでブロックチェーンや IPFS の話しをしました。その仕組みの応用というかマッシュアップ（合わせ技）の新しい試みに NFT というものがあります。

とは言え、NFT の概念自体は 2012 年には存在していました。新型コロナの流行った 2021〜2022 年にかけて話題になったので記憶に新しい方も多いかもしれません。

まずは NFT の実物を見てみる

何はともあれ、「NFT といえば」というものを実際に見てみましょう。

世界的に有名なオークションハウスのクリスティーズで、2021 年の 3 月に、6,930万ドル（時価 75 億円）で落札された NFT 作品です。

"EVERYDAYS: THE FIRST 5000 DAYS" by Beeple @ Christies Online

上記クリスティーズのサイトを開くと、作品のサムネイルが表示されたと思います。

この作品は Beeple（本名: Mike Winkelmann）という作家さんのものです。彼自身の "EVERYDAYS" という「1 日も・・・欠かさず、毎日 1 枚のデジタル作品を描き続ける」というアート・プロジェクトのうち、最初の 5000 日間（13 年ぶん）の画像を 1 枚にしたコラージュ作品です。

Beeple 氏は性格は明るいものの、どこかヤサぐれた感じが漂う、媚びない姿勢のアンダーグラウンドな作家で、一部のマニアには人気でした（とは言っても、すでに 180 万人のフォロワーがいたり、有名ブランドやアーティストともコラボレーションしているのでアンダーグラウンドとも言えないのですが）。

そして、この作品が話題になったのは、これを「天下のクリスティーズ初の NFT 作品として出品された」ことと、100 ドルで始まったオークションが「6,930万ドルで落札された」ことです。

実は、この出品された作品の高解像度のデータは IPFS 上で公開されています。つまり、誰でも作品にアクセスおよびダウンロードできます。

EVERYDAYS: THE FIRST 5000 DAYS の RAW Jpeg データ（300MB 以上あるので注意）
- CID: QmXkxpwAHCtDXbbZHUwqtFucG1RMS6T87vi1CdvadfL7qA
  - （CID については先述している IPFS の概要をご覧ください）

「誰でも見れるってことはコピーし放題じゃん」と、これだけでは「何が NTF なんだ？」となると思います。

さて、アーティストやメディアが勘違いしているのが「この作品の高解像度データがオークションに出された」と思い込んでいることですが、違います。

先ほどのクリスティーズのサイトで、サムネイルの下にある DETAILS の項目を開いてみてください。

そこに記載されている token ID の 40913 という 5 桁の数値がオークションに出されたのです（これらが何であるかは順に説明していきます）。

他の絵画などのオークション品の DETAILS と内容を比べてみてください。この作品は、他の絵画と違い non-fungible token (JPEG) なるものが競せりに出されているのがわかります。

これらを理解する前に、まずは NFT の情報を探る方法から入りましょう。

耳慣れない用語が出てくると思いますが、各々の用語の説明や、何をしているかは追って説明して行きます。まずは、耳慣れない用語を耳に馴染ませる程度の感覚で、お読みください。可能なら PC ブラウザで触りながらがベストだと思います。ゴロ寝しているなら、脳内操作しながら、お暇な時に触ってみて下さい。

NFT 情報の調べ方（`Ethereum` ベースの NFT の場合）

クリスティーズの出品ページにある DETAILS を見ただけでは「non-fungible token なるものが競りに出されている」以上の情報がありません。

DETAILS の、さらに下の項目の SPECIAL NOTICE を読むと、支払いは Ether でも支払えることがわかります。

Ether は仮想通貨の 1 つで、Ethereum ブロックチェーンを利用した暗号資産です。このことから、今回の作品は Ethereum 上のブロックチェーンに登録された NFT であることがわかります（ブロックチェーンの概要は先述しているので、そちらをご覧ください）。

そのため、今は Ethereum ベースで説明しますが、NFT を構成する情報の「キーポイント」は、どれも同じなので、気になる NFT サービスがあれば該当する用語に置き換えて下さい。

まずは、上記でも述べているクリスティーズの出品ページの詳細（DETAILS）を開き、以下の項目を確認してください。

token ID ... Ethereum 上の作品 ID（ぶっちゃけ、これが NFT）
wallet address ... 作品 ID に紐づいた作者の Ethereum ウォレットの ID
smart contract address ... 作品に紐づいた取り引きのルール（自動処理されるスクリプト）の ID

まずは、NFT を発行した人（この場合、作者）の Ether のウォレット（秘密鍵に紐付いた口座）の情報を見てみましょう。Ether と Ethereum を扱うサービスなら、どれでも確認できるのですが、今回は etherscan.io を利用します。

https://etherscan.io/address/0xc6b0562605d35ee710138402b878ffe6f2e23807 @ etherscan.io

まず、タイトルから Beeple が確認できます。

本当に本人のアカウントであるかは、さまざまな情報から総合的に判断する必要があります。残念ながら Beeple 氏の公式サイトにはウォレットのアドレスが明記されていないので、今回は、クリスティーズの公式サイトがハッキングされていないことを前提として、Beeple 本人のアカウントとして話を進めましょう。

次に ETH BALANCE の項目で、このアカウントが所有している Ether 量と、ETH VALUE で、その価値（現在の為替レートから算出した米ドル額）が確認できます。しかも、このウオレットの出納帳（取引記録）までもタイムスタンプ付きで確認できちゃうのです。

これは、税務署や富裕層などからすると、とんでもない事だとお気付きでしょうか。つまり、このアカウントを所有していると主張するなら、その取引内容まで全て晒さらすということでもあるのです。

重要なのが、Ether が利用している Ethereum のブロックチェーンは、分散型でパブリックです。つまりオンプレミスではない（特定の企業が囲い込みをしていない）ので、今回のように誰でも、いつでもデータをダウンロードや参照することができます。

それでは、次に Ethereum のブロックチェーンから、この作品の取り引き情報を覗いてみます。

Ethereum の DB（ブロックチェーン）は誰でもダウンロードできるためデータの調べ方はいくつか方法があるのですが、DB をダウンロードしても重いし煩雑になるので、先ほどのウォレットの確認と同じように Web 上から検索できる etherscan.io を通して調べてみたいと思います。

https://etherscan.io/

クリスティーズのサイトにあった「smart contract address」の値（0x2a46f... から始まる値）をコピーして、上記サイトの "The Ethereum Blockchain Explorer" の下にある検索窓にペーストして検索します。

すると Transactions（取り引き）タブが選択された状態で、ズラりと表が表示されたと思います。

この「Transactions にある一覧は何か」の説明の前に、まずは Contract（契約）という用語を理解する必要があります。

スマート・コントラクト

Transactions（取り引き）タブの、右 4 つ隣にある Contract（契約）タブを開いてみてください。

Contract | Address 0x2a46f2ffd99e19a89476e2f62270e0a35bbf0756 | MakersPlace: MKT2 Token @ etherscan.io

Contract Source Code (Solidity) という項目に、なんやら謎のスクリプトが記載されていると思います。

Contract Source Code（契約のソースコード）とあるように、これは Ethereum のブロックチェーンにデータを書き込む際に使われるスクリプトのソースコードで、Solidity というプログラム言語（スクリプト言語）が使われています。

恐れずに言えば、ブロックチェーンにデータを書き込む際に実行されるバッチやマクロのようなものです。

つまり、指定された Contract のスクリプトが無事実行され、ブロックチェーンに書き込まれることを「契約」と呼んでいるのです。そして、自動化されていることから、この仕組みを Smart Contract（スマート・コントラクト）と呼びます。

実は、このスクリプトも Ethereum のブロックチェーンに書き込まれています。今回の操作は、その中身（ソースコード）を確認したことになります。

そのため、Smart Contract の ID（ハッシュ値）が同じ場合はスクリプトの内容も同じとなるため、ブロックチェーンの仕組み上、スクリプトが改竄かいざんされることはありません。

逆に言えば、バグや脆弱性が含まれていた場合でも修正することもできません。

ここでは「スクリプトが何をしているか」よりも、このスクリプトを使ってブロックチェーンに書き込まれた履歴が、さきほどの「Transactions にある一覧は何か」であることに注目します。

つまり、今回の作品に限らず、このスマート・コントラクトを利用した取り引き（Transaction）が一覧で確認できるということです。

Transactions of 0x2a46f2ffd99e19a89476e2f62270e0a35bbf0756 @ etherscan.io

取り引きするデータを探す（対象となる NFT 情報の確認をする）

ご覧いただいているように、このスマート・コントラクトを利用した取り引きはたくさんあります（DB 登録スクリプトの実行ログ、つまり Transaction）。

そこで、今回の作品（取り引きの対象物となる NFT）を探ってみたいと思います。つまり、契約（Contract）を確認するということです。実は、データベース（ブロックチェーン）の検索も、スマート・コントラクトのスクリプトを使って行います。

再度、先ほどの Contract タブを開いて Code の隣にある Read Contract を選んでください。実行可能なスマート・コントラクトの読み取り系の関数（メソッド）が表示されます。

Read contract of 0x2a46f2ffd99e19a89476e2f62270e0a35bbf0756 @ etherscan.io

関数一覧から、23 番目の tokenURI を開くと入力フォームに _tokenId (uint256) という項目があるので、作品の token ID である 40913 を入力し、Query ボタンで問い合わせます。tokenURI の関数が実行され、おそらく以下のような結果が出ると思います。

ここで注目して欲しいのが、戻り値の「string: ipfs://ipfs/QmPAg1mjxcEQPPtqsLoEcauVedaeMH81WXDPvPx3VC5zUz」です。

つまり、DB（Ethereum）に NFT 40913 を問い合わせると文字列が値として紐付いていた、そして、その値は IPFS の CID だった、というだけのことです。

それでは、HTTP のゲートウェイ経由で IPFS のコンテンツを確認してみましょう。

https://ipfs.io/ipfs/QmPAg1mjxcEQPPtqsLoEcauVedaeMH81WXDPvPx3VC5zUz

でかい画像が表示されるかと思いきや、「え？JSON？」となると思います。

このままでは、内容が把握しづらいので整形したものを以下に置きます。JSON の各要素をザッとチェックしてみてください。

下の方にある raw_media_file 要素の値に、作品の生データ（高解像度データ）が IPFS の CID で記載されているのが確認できます。また digital_media_signature（デジタル・メディア署名）に、この画像の SHA-256 のハッシュ値を使っていることも確認できます。

QmPAg1mjxcEQPPtqsLoEcauVedaeMH81WXDPvPx3VC5zUzの中身

{
  "title": "EVERYDAYS: THE FIRST 5000 DAYS",
  "name": "EVERYDAYS: THE FIRST 5000 DAYS",
  "type": "object",
  "imageUrl": "https://ipfsgateway.makersplace.com/ipfs/QmZ15eQX8FPjfrtdX3QYbrhZxJpbLpvDpsgb2p3VEH8Bqq",
  "description": "I made a picture from start to finish every single day from May 1st, 2007 - January 7th, 2021.  This is every motherfucking one of those pictures.",
  "attributes": [
    {
      "trait_type": "Creator",
      "value": "beeple"
    }
  ],
  "properties": {
    "name": {
      "type": "string",
      "description": "EVERYDAYS: THE FIRST 5000 DAYS"
    },
    "description": {
      "type": "string",
      "description": "I made a picture from start to finish every single day from May 1st, 2007 - January 7th, 2021.  This is every motherfucking one of those pictures."
    },
    "preview_media_file": {
      "type": "string",
      "description": "https://ipfsgateway.makersplace.com/ipfs/QmZ15eQX8FPjfrtdX3QYbrhZxJpbLpvDpsgb2p3VEH8Bqq"
    },
    "preview_media_file_type": {
      "type": "string",
      "description": "jpg"
    },
    "created_at": {
      "type": "datetime",
      "description": "2021-02-16T00:07:31.674688+00:00"
    },
    "total_supply": {
      "type": "int",
      "description": 1
    },
    "digital_media_signature_type": {
      "type": "string",
      "description": "SHA-256"
    },
    "digital_media_signature": {
      "type": "string",
      "description": "6314b55cc6ff34f67a18e1ccc977234b803f7a5497b94f1f994ac9d1b896a017"
    },
    "raw_media_file": {
      "type": "string",
      "description": "https://ipfsgateway.makersplace.com/ipfs/QmXkxpwAHCtDXbbZHUwqtFucG1RMS6T87vi1CdvadfL7qA"
    }
  }
}

Token ID、Wallet ID、Contract ID の関係性

さて、ここで先に出てきた 3 つの項目を整理したいと思います。

token ID: 40913
wallet address: 0xc6b0562605D35eE710138402B878ffe6F2E23807
smart contract address: 0x2a46f2ffd99e19a89476e2f62270e0a35bbf0756

Ethereum 上で Token ID なる謎の数値が発行され、発行者のウォレット ID が wallet address で、Token ID をゴニョゴニョする際に使われるプログラム（スクリプト）の ID が smart contract address です。

そして、どうやら Token ID が Ethereum の NFT であるということ。実態は JSON データで、データの中に作品の CID が記載されていることがわかりました。

つまり、RDB のように、作家や作品の情報（ウォレットや IPFS の CID）が紐付けされており、紐付けを理解していないと探すのにも大変なのも RDB と似ています。

1 つ 1 つの技術（ハッシュ関数、ブロックチェーンや IPFS などの基本）が理解できていないと、これから説明する NFT の本質や強みも理解できませんが、紐付け先が「内容の変更が不可能な IPFS の CID」であることがポイントです。

と言うのも、NFT に登録する値は文字列ということは、IPFS の CID ではなく URL にすることも可能ということです。つまり、コンテンツではなく場所（サーバ）を登録することもできるということです。

鋭い人は「あ。囲い込みや、詐欺に使えるってことか」と、お気付きかもしれません。

URL のドメイン・オーナーが、後から閲覧を課金制にしたり、URL 先のコンテンツを入れ替えたりできるからです。

NFT が詐欺臭い理由

売る人がいて、買う人がいる（商品として扱える）ということは投機対象にもできるということです。

これは NFT に限りません。つまり「転がす」（使うのが目的でなく、転売時の差額で儲ける）ことが目的の場合、株・先物取引・不動産・古物商・外国為替・トレーディングカード・暗号資産などと同じように、経験と知識（金融知識や取り扱い対象の知識）がないと簡単に騙されるか失敗しやすいため、注意が必要なものの 1 つです。

相手から「儲かる」とか「未来の自分への投資」と言った言葉が出てきたら「（怪しい壺を売りつけてきた）」くらいの警戒心を持つようにしましょう。ドルを使ったこともないのに、言われるがままに買ったら「ジンバブエ・ドルだった」みたいなことになりかねません。

とは言え、NFT 自体は「デジタル作品の、作家の利益を守るために生まれたもの」なので、ちゃんと理解しておきたいところです。

ここでは、NFT は「技術的に何をしているのか」、「技術的に何が面白いのか」を中心に話しを進めます。もし、好きなアーティストが NFT で作品を公開しているなら、仕組みと調べ方をしっかり理解した上で作家さんをサポートしましょう。

NFT の基本

NFT を一言で説明すると「アイテムの所有権を管理する分散型の台帳」です。所有権といっても、法的な所有者ではなく、ファイルのアクセス権に近い所有者です。

つまり、「そのサービスにおいて、アイテム ID と紐付いているユーザを現在の所有者とする」ものです。

そして、この時の紐付けをアイテム ID とユーザの公開鍵をブロックチェーンに記録することにより、秘密鍵を持つものが所有者であることを実現しています。ブロックチェーンなので例え管理者であっても過去の記録を消すことはできません。

とは言え、やっていることはシンプルで、最低限 2 つのテーブルを持った DB で管理できます。

発行されたアイテム ID の一覧を保持するテーブルと、その ID に紐づいた公開鍵を管理するテーブルを持ったものです（実装方法は NFT のサービスによって異なります）。

つまり、「アイテム ID xxx の現在の所有者は、秘密鍵 yyy を持ったユーザーである」といった方法で所有権を管理しています。「●●● の NFT を〜した」というのは、「●●● というアイテムの所有権を〜した」という意味になります。

そして、この時に使用する公開鍵・秘密鍵を、暗号資産に使われるウォレットの鍵を使うことで、暗号通貨による売買取引と所有権の移行を同時に行うことができます。大半の場合の NFT はこのタイプです。

ここで注意すべきは「所有権」であり「著作権ではない」ことです。

例えば、デジタル音楽を購入するというのは「再生する権利」を購入して所有しているのであり「著作権や複製権を購入しているのはない」のと同じです（詳しくは後述します）。

このように、「とあるハッシュ値が現在誰のウォレットに紐づいているか」をブロックチェーンで管理することで、ハッシュ値の所有権を確認することができます。また、所有権といっても、その権利は基本的に、その NFT のサービス内に限定されます。

しかし、作品の作業・制作記録をアーカイブしておき、そのハッシュ値をアイテム ID として NFT に登録しておけば、著作権侵害で訴えられた際に「創意工夫して作成したものである」という証拠の 1 つになります。もちろん、NFT でなく直接ブロックチェーンにハッシュ値を刻んでも構いません。

というのも、ブロックチェーンの仕組み上、登録時間は改ざんできないし、秘密鍵を失くしたり盗まれたりしない限り自分が登録したものであると技術的に証明できるからです。

逆に言えば、非公開ブロックチェーンを利用した（情報履歴が直接見れない） NFT では意味がないということでもあります。

先述したようにブロックチェーンとは、「コスト」（計算量、時間、電気代、記憶容量）と引き換えに「分散」と「インセンティブ」（マイニング）により、誰も信用できない環境における情報の堅牢性を実現しています。

非公開ということはオンプレミスでプロプライエタリということでもあり、改ざんに対する客観的な確信が持てず、かつ倒産したら消えるブロックチェーンということです。

そもそも、非公開なら別にブロックチェーンを使わずとも、もっとコストも低く、処理も速く同じことができますし、枯れた技術（堅牢で実績のある技術）もあります。

関連会社や系列会社間の閉鎖的なブロックチェーンならいざ知らず、あえてコストの高いブロックチェーンを非公開で一般ユーザに使わせるということは、プロプライエタリがゆえ技術的に不安なども含め、何かしら後ろめたい、もしくは隠したいことがあるからか、ユーザの「合理的無知」を利用した金の匂いしかしません。

「A 社の NFT が他社でも使えるか。別のサイトでも取引が確認できるか」が見極めのポイントになるかもしれません。

以上のように、NFT は「暗号通貨のコインの代わりに、アイテム ID に置き換えたブロックチェーン」とも言えますが、通常は暗号通貨のブロックチェーンとは異なるものの、セットで管理されるブロックチェーンです。

このことから、NFT はブロックチェーン技術の 1 つの活用法とも言えます。

例えば、映画館や劇場のチケットなどで活用する場合を見てみましょう。

ちなみに、ここで言う「ウォレット」とは「秘密鍵を持っている人」と同義で、「ウォレット間の移動」は「アイテムに紐付いた公開鍵の変更」がブロックチェーンに記録されたと同義です。

上映分のアイテム ID（ハッシュ値）を NFT として発行する。
会場の座席番号をアイテム ID と紐づけておく。
ユーザーが座席を購入すると、アイテム ID の所有権が映画館のウォレットからユーザーのウォレットに移動する。
入場時に、アイテム ID がそのユーザーのウォレットに紐づいているか確認する。
紐づいていた場合は、ユーザーのウォレットから映画館のウォレットに移し、入場できる。

ここで、「え？コンサートの電子チケットと同じやんけ」と気づいた方もいると思います。もしくは「ブロックチェーンをキー・バリュー型の DB として使ってるだけやんけ」と。

鋭い。私は「ほえー」と感心するだけでした。

言われてみると、確かに同じです。

従来の電子チケットも、NFT も、購入方法は同じです。現金を一旦ポイントやクレジットもしくは暗号通貨に換金し、そこから対象物を購入（取り引き）します。取り引きが成立して、お互いに出金・入金が確認されると、対象物は相手のアカウントに移されたり郵送されます。

やはり、一番の違いは、ブロックチェーンを利用していることでしょう。

つまり、出金・入金と同時にアイテムの ID とウォレットの紐付けが完了するため、NFT チケットの所有権の移動が台帳として刻まれているということです。そのため、「支払ったのに発送されない」といったトラブルもありません。

コンサートの電子チケットの場合は、購入時に顔写真や身分証明を添付しておき、入場時に照会することで転売対策をする必要がありました。有効ではあるものの、プライバシー保護は電子チケットの発行側や開催会場側の、会社やスタッフのセキュリティー意識に依存します。

ブロックチェーンの場合、ウォレットの公開鍵（厳密には秘密鍵）が身分証として機能し、ウォレット間の移動も確認できます。そのため「一つのウォレットが大量に購入して不特定多数に転売している」なども追跡できるため、転売屋（のウォレット）を特定することが容易になったり、移動履歴を見れば転売チケットであるか確認することができます。

このような仕組みをプロプライエタリで自社開発してもいいのですが、イーサリアムなどのオープンソースで既存のシステムを使う方が汎用性・継続性・信用性が増します。イーサリアムなどの最新のブロックチェーンは暗号通貨だけでなく、NFT（一意のハッシュ値）の発行と管理もできる仕組みを持っているからです。

イーサリアムの場合、この「ハッシュ値の発行処理」を mint（鋳造ちゅうぞう）という言い方をし、アイテム ID のウォレット移動や、移動時の処理を「スマート・コントラクト」と呼びます。移動処理には暗号通貨で手数料が取られますが、金融機関同様に自社インフラで開発しても発生するコストです。問題はどこでペイ（回収）するかの違いだけです。

NFT のメリット

デジタル作品を NFT 化するメリットですが、大きく 2 つあります。

アイテムに対する「所有権の売買」（アイテム ID のウォレット間移動）が可能である。
「転売されても作者にマージンが行く」仕組みがある。

これにより、コピーして転売しても「所有権」を持っていなければ、たとえデータの内容がまったく同じであってもコピーを違法コピーと断定できます。また内容をいじってハッシュ値が変わったとしたら贋作と断定できます。

「え？でも、コピーして売っちゃえば（コピーを一般公開しない限り）問題ないのでは？」と感じると思います。

CD レンタルや中古本でも、そうであるように、個人利用であればコピーを持つこと自体は違法ではありません。問題は、転売時に作家さんにマージンが行かないことです。ここで言うマージンは、売り上げから作者へ行く取りぶんのことです。

NFT はスマート・コントラクトのスクリプト内容により、転売時の取り引きで作者にもマージンが渡るようにできます。

おそらく、これが NFT の一番の強みだと思います。

`NFT` はコピーできる

NFT を「デジタル・データをコピーできない技術」と言っているメディアもありますが、違います。コピーできます。

しかし「100% 同じデジタル・データなのに、どちらが本物かを証明できるインフラ」が NFT なのです。技術と言わずインフラと呼んでいるのは、実装方法は問わないからです。イーサリアム団体なども、これを制定化する動きがあり、おそらく組織規模からデファクト・スタンダードになるとは思いますが、「イーサリアムの NFT = NFT」ではありません。

もちろん NFT のデメリットもあります。

1 つは「電子署名を知らないといけない」ことです。これは、著作権を守るために作家自身が近代的なサインの入れ方（電子署名の仕方）を覚えないといけなかったり、作品の購入者は公開鍵の出どころと、署名の確認の仕方を覚える必要があるということです。

なぜなら、誰でも NFT でデータを公開できるため、勝手に NFT 化されることが多々あるため、作者自身がオリジナルであることを証明する努力が必要になります。例えば、作家のホームページ、SNS のプロフィールや出版社の紹介ページなどに公開鍵を公開する・作品には必ず電子署名を添えるなどです。これにより、作品が電子署名されていた場合、ユーザーは作家の公開鍵で検証できます。

2 つ目のデメリットは「秘密鍵という単一障害点がある」ことです。これは NFT や暗号資産に限らず近代的なセキュリティ全般に言えることなのですが、セキュリティの全てが「秘密鍵」に依存しています。つまり、秘密鍵を紛失してしまうと元も子もない世界なのです。

マイナンバーカードやパスポートと同じ、もしくはそれ以上に保管・紛失・流出・盗難に注意する必要があります（むしろ、年度ごとに鍵を作り直し、あえて秘密鍵を破棄してしまい。「●●年度の作品」と割り切ってしまうのもありかもしれません）。

さて、ほとんど復習なのですが NFT の仕組みを理解するのに必要なポイントが 4 つあります。

ファイルのハッシュ値
公開鍵と秘密鍵による暗号化・復号と署名
ブロックチェーンの DB による所有権の移動記録（変更が不可能な取引台帳）
IPFS による公開鍵、署名やコンテンツなどの配布

これらは本記事で説明済みですが、理解していると NFT は以下のようなものであると説明できます。

デジタル作品（データ）にシリアル番号を埋めてハッシュ化した値を「トークン」とする。
トークンもしくはシリアル番号付きデータを、著者（作家もしくは著作権関係者など）の「秘密鍵」で署名する。
トークンの所有者と署名ファイルをブロックチェーンで管理する。
著者の「公開鍵」によって署名が確認でき、所有者も確認できる。

トークンについては後述しますが、これによりネットに出回っているデジタル作品の「公式」な所有者が確認できます。

つまり、データのハッシュ値（ここではトークン）および著者の公開鍵による検証が通れば、そのデータは改竄されていない（偽物でない）ことが確認できるのです。

そして、そのハッシュ値を専用のブロックチェーンの DB で確認することで、その作品の「公認の所有者」であることが保証されます。

投資における NFT は、この所有権（トークン）を絵画や骨董品と同じ仕組みで売買しているのです。

しかし、NFT と暗号資産を適切に組み合わせることで、従来の絵画や骨董品の売買といったものと違うメリットが出てきます。

おそらく、その組み合わせの最大のメリットは、その後、NFT 作品が転売されても作家にマージンが入るということでしょう。（NFT サービスによって異なりますが、後述するイーサリアム・ベースの NFT の場合は仕組み上できるはずです）

これは、古本など中古品商売で泣いていた作家さんを救済できる可能性を秘めています。このことを聞かされず NFT を勧めてくる業者・出版さんがいたら、作家さんは要注意です。不要なマージンを抜かれていると思います。

最近ではデジタル作品に限らず、研究に使われるような個人データの取り扱いなどにも NFT は注目を浴びています。

「特殊な体質や病症のため検査をさせて欲しい」と取得した患者のデータを、病院が別の研究機関に有償で提供しているケースなどです。「研究のため」という名目でサインしているのと、基本的な個人情報は削除されているため患者の知らぬ間に行われます。

これら貴重なデータを、情報を提供した患者さんにもきちんと還元されつつ、広く活用・アクセスされるようにといった動きです。

NFT の所有データはブロックチェーンで共有・管理されますが、対象となる本体のデータは、別なので気を付ける必要があります。

一般的に、本体データは IPFS 上のネットワークや、サーバを用意して従来のデータ提供方法で行われます。他にも、作品自体にチップや QR コードの入った物理的な媒体で提供したり、トークンを持っている人のみダウンロードできるサーバで提供されたりします。これもサービス会社によって違います。つまり、NFT であっても、会社が潰れればアクセスできなくなる可能性があるのです。

「インターネット」や「ブロックチェーン」同様、NFT という商品や特定サービスや会社を指すわけではありません。インフラの仕組みの 1 つです。「NFT を提供していた会社が 1 つ消えた」というのは「プロバイダが 1 つ消えた」と、なんら違いはありません。

恐れずに言うと、NFT は著者がデジタル作品に「証明書」を添えることで、作者の公開鍵により「鑑定書」（もしくは「保証書」）の役割を果たし、現在の所有者をブロックチェーンで確認できる「仕組み」です。

NFT の強みは「所有者を確認できる仕組み」です。何度か言及しているように、コピーされて、内容が 100% 同じデータが市場に出回ったとしても「贋作」と認定できる仕組みなのです。同じ作品でハッシュ値が違えば、そもそも「贋作」ですし、ブロックチェーンの DB 上の所有者が違えば「盗品」です。

次に本質的に重要なのが「著者が公式な場において公開鍵を公開していること」と「作品データの署名を公開していること」が大前提であることです。NFT と言えど、対象データは著作物です。そのため、必要であれば違法コピーに対する逮捕につなげる情報にも使えます。

そのため NFT の本来の目的は以下の 2 点と言えます。

デジタル作品を所有することに価値を見い出すコレクターを保護するためのもの。
デジタル・アーティストの作品に対するリスペクトを示すもの。

しかし、現在は、日本でのラッセンに代表される「絵画商法のように使える」と、これに目を付けた企業が「後生大事に使いもしないデュエルカードに大金を出すような人々をターゲット」に参入しているので注意が必要です。

くどいのですが、本来の目的は「デジタル作品に対するファンのリスペクト」であることを念頭に置いてください。

NFT の意味

NFT とは Non Fungible Token の略で「等価交換できない類いのトークン」という意味です。

巷ちまたでは「非代替性トークン」と言われるので、「コピーできないもの」的な誤解が生まれているのだと思います。

「トークンとは何か」の前に、ここでいう「等価交換できない」（Non Fungible）の「等価交換」（Fungible）について先に説明します。「トークン」の説明は、そのあと行います。

まず、「等価交換」（Fungible）とは、金や銀などのように「形が違ったり変わっても同じ質量であれば同じ価値を持つため交換できる」ということです。

つまり、100g の金の塊と 100g の金の指輪は同じ金の値段を付けられる（価値がある）ということで、その場合に Fungible と言います。

同様に、10 枚の 100 円玉と 1,000 円紙幣は交換可能なので Fungible つまり「等価交換可能」と言えます。また、為替レートに合わせてドルと円の交換や、ドルとビットコインの交換はできるので Fungible となります。

元々はラテン語の fungi（そのものを楽しむ、価値を見い出す）から来ており、「形が変わっても楽しめる、価値がある」ものの意になりました。（ちなみに、真菌の fungus とは語源が違い、別のものです。真菌の fungus はスポンジと同じ語源の spongos から来ています）

逆に言えば、装飾や造形といった「形」に価値がある場合などは、Non Fungible ということになります。

例えば 100g のプラスチックと有名モデラーが組み立てた 100g のガンプラは「等価交換できない」（Non Fungible）ものと言うことになります。絵画なども、同じ質量の絵具と紙とは「等価」ではありません。アイドルが付けていたカチューシャと、私のカチューシャが同じであっても、そのアイドルのファンから見れば「等価」ではありません。

同様に、16 桁のハッシュ値と、それを並べ替えた値は「等価ではない」（価値が違う）ので Non Fungible となります。逆に 16 進数のハッシュ値と同じ値の 10 進数のハッシュ値は「等価」（価値が同じ）なので Fungible となります。

身近な例で言うと、1,000 円札の通し番号が異なっても同じ 1,000 円の価値を持つのが Fungible です。しかし、通し番号が 0000001 など、番号に価値を感じる場合は Non Fungible となり 1,000 円（等価）ではなくなるのです。

このように、Non Fungible Token は「『等価交換できないもの』のためのトークン」という意味になります。

転じて「唯一無二を示すためのトークン」となり、誤解を招きかねない「非代替性トークン」とカッコ付けた日本語名が付いているのです。

ちなみに、話題のイーサリアムは、コインなどの Fungible トークンと、一意性を持った Non Fungible トークンを発行することができます。どちらもハッシュ値で、DB や配列のキーのように使えるものですが、前者は「（1 コインの）ハッシュ値を交換しても価値が変わらないタイプ」、後者は「（1 NFT の）ハッシュ値を交換したら価値が変わるタイプ」と考えると理解がスムーズでしょう。

では、肝心の「トークン」とは何でしょう。

トークンの意味

「トークン」ですが、これも一言で説明すると「同じ価値観を持つもの同士でのみ・・通用する・価値を持つ、何かの発行物」をトークンと言います。

その「何か」は何でもいいのです。例えば、ゲームのコイン、遊園地の入場チケット、銀行のワンタイム・パスワード、ハッシュ値、などです。

そして「同じ価値観を持つもの同士でのみ・・通用する」というのは、例えばモノポリーのお金をゆうちょ銀行に持っていっても振り込めないようなものだったり、USJ のチケットでは TDL に入場できなかったりするようなものです。

我々の業界で言えば、アクセス・トークンは同じサービスでは価値があり、異なる環境ではだたのランダムな数値でしかないのと同じです。

シリアル番号による価値化

NFT の詳しい仕組みの話しの前に、シリアル番号と価値についても少し説明します。

トレーディング・カードゲームなどでは、個数限定のカードが発行されたりすることがあります。「1/100」（100 枚中 1 枚目）といったシリアル番号が振られているアレです。アートの世界ではシルクスクリーン作品や版画の作品などでも見かけます。

これは「複製可能な作品にシリアル番号を付けることで付加価値を付けている」のです。

さて、「複製可能な作品」の代表格と言えばデジタル作品です。

データのコピーなんて誰でもできてしまいますし、コピーガードとして DRM なども有名ですが、ガードが外れてしまえば同じことです。

このこと（DRM 解除）は、そもそも違法ですし、何よりデジタル作品を作る作家さんの収入を減らすことにもなりかねません。しかも、デジタルであることから、どれがオリジナルなのかも判断が難しくなります。

例えば、自分の好きな作家さんが亡くなり、未発表の描き下ろしデジタル・イラストがネットに公開され、その作品にとても感銘を受けたとします。しかし、ネットに公開されている以上、誰でもローカルに保存できてしまいます。

では、デジタル作品を「作品」として存在させるにはどうすれば良いのでしょう。

NFT は、その 1 つの可能性を示すものと言えます。

例えば、デジタル作品・作者による署名ファイル・公開鍵などをセットにしたものをチップやメモリに焼き、「使用していたペン先」や「髪の毛」など、なんでもいいので付加価値を付けて物理的に n 個、セットとして作成します。レイヤーデータなども付いていたら最高の付加価値だと思います。

そして、各々のセットの作品にはシリアル番号が描かれてあり、そのデータのハッシュ値を作者の秘密鍵で署名したもの、もしくはデータと秘密鍵をセットでハッシュ化したものをトークンとして確認できるようにするなどです。

NFT のサービスによってはセットからワンタイム・パスワードも確認できるようにして、それらを使ってサーバにアクセスすると作品が閲覧できるようになっていたり、物理的なセットではなく単純にオンラインでデータをダウンロードするタイプがあったりと、ここら辺はサービスによって異なります。

データのシリアル番号、ハッシュ値と所有者の追跡ができれば、物理・オンライン、方法論は何でもいいのです。

そして、各セットを作品としてオークションにかけるのです。もちろん 1 点いくらで売っても構いません。

落札・購入した人は、このセットの所有者となりトークンと紐付けられブロック・チェーンの DB に保存・共有されます。

いくらで売られたかは関係なく、あくまでも「トークンの所有者が誰であるか」が確認できるようになっているのです。

支払いは現金でも仮想通貨でも構わないのですが、「支払い」「ブロックチェーンへの記録」「NFT 情報を記録できる」「転売された時にマージンを作家に送る設定ができる」などを 1 つでできることから Ethereum が多く使われます。

権利の追跡としての NFT

NFT の仕組みを知らなくても、知っておかないといけない重要なことがあります。

それは NFT は著作権（複製権や著作隣接権）の譲渡ではないことです。つまり、あくまでも「トークンの所有を示すも」のである、と言うことです。

とは言え、複製権や著作隣接権といった権利も、作品のトークンから理屈上は NFT で管理できるので、近い将来に契約履歴専用のブロックチェーンに進化するかもしれません。

しかし、重要なことなので繰り返しますが、「お金を払ったんだから、その NFT 作品のグッズを作ったりビジネスしても良い」と言う考えは「CD を買ったから俺のもの。だからコピーして売っても良い」「グッチのバッグを買ったから私のもの。だから同じ柄のカバンを自分で作って売っても良い」と言う考えと同じで、思いっきり違法です。

また、作者非公認で勝手に NFT として出す業者も出てくるでしょう。

購入する側は作者公認なのかを確認する必要がありますし、デジタル・アート作家も「よく知らないけど秘書が勝手にやりました」的な結果にならないように勉強が必要です。公開・秘密鍵によるデータの署名の仕方くらいは知っておいた方がいいのではないでしょうか。

NFT が話題になったのは Beeple や Beeple-Crap 名義で有名な Mike Winkelmann 氏が NFT 作品群をオークションに出したところ、総額 75 億円で落札されたことからです。

これが、ビットコインなどの暗号通貨（仮想通貨）の投資家の「NFT は次のビジネスになる」と投資対象としても話題になっていたり、俺様暗号通貨の発行に躊躇ちゅうちょして出遅れていた企業が、暗号通貨よりわかりやすい商材ということもあり「オタク相手の古くも新しいビジネス」の匂いを感じ張り切っているからなのです。

そのため、「いま NFT が熱い」と購入を薦められたら「将来、高い値段が付くから、自己投資として 1 枚は持っておくべき」とラッセンの絵の購入を薦められるようなもの、と考えて良いと思います。

金額だけがメディアに取り沙汰されるのですが、Beeple 氏は 2007 年から "Everydays" と言う作品シリーズで「毎日」欠かさず 1 作品をネットに上げることを 14 年以上続けて来たのです。「振り込めない詐欺」を繰り返してきた氏に対するファンの気持ちが値段に反映したものなのです。

Beeple Crap 公式サイト @ beeple-crap.com
- Beeple 氏の NFT 作品のセットの例

つまり NFT で作品を出したから売れるというものでもないのです。

しかし、これは DLsite やとらのあなで作品を出しても同じことです。

逆に言えば、ファンが付いた場合は、よりファン心ごころをそそるサービス（付加価値）を NFT では提供可能であるということでもあります。

何度か言及していますが、イーサリアムなどを使ったタイプの NFT では転売されると作家にマージンが入るものがあります。つまり、いまのようにデジタル漫画や動画をオンラインで購入しても、それが NFT であれば中古として転売できるし、転売されても作家にマージンが入る世の中になる可能性がある、ということです。

（テレビでジブリ作品が定期イベントのように流れますが、放送されるたびにジブリ・スタジオや宮崎駿先生にいくら入るのか調べてみてください。また、なんとか屋やブック・なんとかで売られている中古本や中古 DVD が売れるたびに、作家にいくら入るかも調べてみてください。ビックリすると思います）

そのため、「お気に入りの作家さんをファンとして支援する 1 つの形」としては、NFT は、とても価値のある仕組みであり、デジタル・データのオリジナル（原本）性を担保する新しい仕組みでもあるのです。

ハッシュ関数の衝突（コリジョン）とセキュリティ

そんな便利なハッシュ関数ですが、「メッセージダイジェストのコリジョン」（異なる入力値なのにハッシュ値が同じという「衝突」）が悩みのタネです。つまり、「改ざんされているのにハッシュ値が変わらない」状態です。

MD5 アルゴリズムの衝突例
- 「MD5 ハッシュ値が衝突する例（Collision Sample of a MD5 Hash value）」@ KEINOS blog
SHA-1 アルゴリズムの衝突例
- 「巷で話題の Google の SHA-1 衝突やってみた」@ 73spica's Blog

しかし、上記記事のように特定のアルゴリズムでハッシュ値が衝突してもアルゴリズムを変えると衝突しません。

ハッシュ値の衝突と回避

アルゴリズムを変えると「衝突しない」と言いましたが限りなく本当に近い嘘ですが、本当です。それでは以下の md5 と sha1 の検証をご覧ください。

MD5 の衝突（検証と実証）

検証実証withPHP

<?php
// MD5 で衝突するサンプルデータ
$str1 = '4dc968ff0ee35c209572d4777b721587d36fa7b21bdc56b74a3dc0783e7b9518'
      . 'afbfa200a8284bf36e8e4b55b35f427593d849676da0d1555d8360fb5f07fea2';
//              ↑                                      ↑
$str2 = '4dc968ff0ee35c209572d4777b721587d36fa7b21bdc56b74a3dc0783e7b9518'
      . 'afbfa202a8284bf36e8e4b55b35f427593d849676da0d1d55d8360fb5f07fea2';
//              ↑                                      ↑

// バイナリに変換
$bin1 = hex2bin(trim($str1));
$bin2 = hex2bin(trim($str2));

// 衝突させる
$algo  = 'md5';
$md5_a = hash($algo, $bin1);
$md5_b = hash($algo, $bin2);
echo ( $md5_a === $md5_b ) ? '衝突しました' : '衝突していません', PHP_EOL;

// 別のアルゴリズムで確認
$algo   = 'sha1';
$sha1_a = hash($algo, $bin1);
$sha1_b = hash($algo, $bin2);
echo ( $sha1_a === $sha1_b ) ? '衝突しました' : '衝突していません', PHP_EOL;

/* 出力結果 */
// 衝突しました
// 衝突していません

「MD5 ハッシュ値が衝突する例（Collision Sample of an MD5 Hash value）」@ KEINOS blog より
オンラインでみる@ paiza.IO

SHA-1 の衝突（検証と実証）

SHA1 の衝突はデータサイズが大きすぎるので paiza.IO で動作サンプルを作れませんでした。簡単なスクリプトとローカルで実行してみた結果結果を載せます。

検証スクリプト

<?php

$url_pdf1='https://shattered.io/static/shattered-1.pdf';
$url_pdf2='https://shattered.io/static/shattered-2.pdf';

$algo = 'sha1'; //衝突する
echo hash($algo, file_get_contents($url_pdf1)), PHP_EOL;
echo hash($algo, file_get_contents($url_pdf2)), PHP_EOL;

$algo = 'md5'; //衝突しない
echo hash($algo, file_get_contents($url_pdf1)), PHP_EOL;
echo hash($algo, file_get_contents($url_pdf2)), PHP_EOL;
exit

実行結果

$ php -a
Interactive shell

php > $url_pdf1='https://shattered.io/static/shattered-1.pdf';
php > $url_pdf2='https://shattered.io/static/shattered-2.pdf';

php > $algo = 'sha1'; //衝突する
php > echo hash($algo, file_get_contents($url_pdf1)), PHP_EOL;
38762cf7f55934b34d179ae6a4c80cadccbb7f0a
php > echo hash($algo, file_get_contents($url_pdf2)), PHP_EOL;
38762cf7f55934b34d179ae6a4c80cadccbb7f0a

php > $algo = 'md5'; //衝突しない
php > echo hash($algo, file_get_contents($url_pdf1)), PHP_EOL;
ee4aa52b139d925f8d8884402b0a750c
php > echo hash($algo, file_get_contents($url_pdf2)), PHP_EOL;
5bd9d8cabc46041579a311230539b8d1
php > exit

`md5` と `sha-1` のセキュリテイについて

先日（2018年夏頃）、とある居酒屋の隣の席で「md5 は破られたから安全ではない」という会話を耳にしました。詳しくは聞いてませんが、「パスワードがバレちゃう」的な話しでした。

しかし、調べてみたら厳密には破られたわけではないようです。いや、確かに破られてはいるんですが。

と言うのも、ハッシュ・アルゴリズムが「破られた」（break）と言われる場合３つの意味があり、業界によって使い方が違うので注意が必要そうです。

ハッシュ前の元の値を計算で出せるようになった

インパクト：大。身元がバレる。

ハッシュ値を衝突させる効率的な方法を見つけた

インパクト：中。身元はバレないが、なりすましされる。

ハッシュ値が衝突する異なる２つの値を見つけた

インパクト：少。単体を狙ったなりすましには有効。

^{🐒 ちなみに、上記の「身元がバレる」と「なりすましされる」の違いですが、ここでは「（ハッシュ値からの逆算で）パスワードがバレてログインされた」と「（ハッシュ値が衝突する）違うパスワードでログインされた」、みたいな違いを指しています。}
^{例えば、「ハッシュ値が衝突するパスワードを見つけた」としても、それは（少なくとも）１つのサービス内において起きることです。その反面、「ハッシュ値からパスワードが逆算できる」となると、同じパスワードの他のサービス全てにアクセスできることになります。（「衝突」に関しては上記「ハッシュ関数の基本と特徴」を参照してください。）}
^{なお、ハッシュ値の衝突を探すことを「攻撃」（attack）と呼んだりしますが、前述のブロック・チェーンなどのように、ハッシュ値の衝突を探すこと自体は全て悪意のあるものではないことを念頭においてください。}

どうやら「md5 が破られた」というのは２番目の「衝突する値の効率的な探し方」を指しているようです。先の md5 や sha-1 の衝突の検証実証例も、その手法を使って発見された値です。

現在（2020年4月）でも、やはり md5も sha-1 も「ハッシュ値から引数の値は逆算できない」状態ではある（１番目の状態は破られていない）ようです。しかし...

増える MD5、SHA-1 脱獄者

しかしながら、時代は「脱 MD5」を経て「脱 SHA-1」に動いており、そして SHA-2 全盛のいまは SHA-3 に変わろうとしています。

例えば、Apple 社内で移植・開発していた OpenSSL の「Apple 版 OpenSSL」を OpenSSL 098-76.200.2 で開発を止やめました。その、主な理由が「SHA-1 をベースにしていたから」です。

同時に、SSL/TLS の暗号通信に使うライブラリ（ハッシュ関数や暗号関数を担うライブラリ）も、ベースを「Apple 版 OpenSSL」から「LibreSSL」に macOS High Sierra（OSX 10.13）から切り替えました。

For this reason, the programmatic interface to OpenSSL is deprecated in macOS and is not provided in iOS. Use of the Apple-provided OpenSSL libraries by apps is strongly discouraged.

^{（OpenSSL | Transmitting Data Securely @ developer.apple.com より）}

ご利用の macOS がどちらのライブラリを使っているかは、ターミナルから $ openssl version コマンドで確認できます。

^{🐒 「開発を止めた」というだけで、Apple 版 OpenSSL の旧バージョン「OpenSSL098-76.200.2」（2016 年版）は Mojave （OSX 10.14.6）の公開ソースコードには、現在でも存在しています。}

また、最近では SSH 接続ツールの OpenSSH も v8.3 から、SHA-1 を使った公開鍵の署名は「将来的に無効になる」旨の表示がデフォルトになりました。

The OpenSSH 8.3 release is out. This primarily a bug-fix release with a handful of minor new features. It does, however, carry a prominent notice that ssh-rsa signature algorithm will be disabled in "a near-future release".

^{（OpenSSH 8.3 released (and ssh-rsa deprecation notice) | LWN.net より）}

^{🐒 元記事が素人向けにわかりやすく書いていないこともありますが、いくつかの記事で SSH で RSA 公開鍵が使えなくなるなるような記載がありますが、違います。}
^{ssh-rsa というのは、SSH 通信において SHA-1 を使って作成された RSA 公開鍵の「署名ファイル」のことで、SSH でログインすると接続先サーバーに保管される署名ファイルのことです。RSA 暗号自体のことを指すわけではありません。}

なぜ、みんな「脱 MD5」「脱 SHA-1」を目指しているのかと言うと、とある・・・論文のせいです。

先の sha-1 の衝突実証ですが、そのデータは Google が見つけたものです。その手法は、発見から 10 年以上前に発表されたとある・・・論文をベースに世界の暗号学者や Google が改良を重ねたもので、Google のクラウド力りょくを利用すれば 13 万米ドル（約 1,400 万円）程度で衝突を発見できることを証明したのです。

たかが１つの衝突に 1,000 万円以上かかるというのは、個人としては大きな金額かもしれません。しかし、大企業が広告費を億単位でかけるのはザラであることを考えると、決して大きい金額というわけでもないことがわかります。

逆に言えば、とあるサーバーの、とあるユーザーの SSH 接続をターゲットにした場合、10 数万ドルもあればハッキングできてしまう可能性があるということです。そして、それだけのコストをかける価値のある情報を持った企業や行政機関は狙われる可能性がある、ということでもあります。

とある女性暗号学者の衝撃論文

md5 は以前よりオワコンと言われていたのですが、ダメチンと言われる大きなキッカケとなった、いや、むしろ止とどめを刺した 2 つの論文があります。

王小雲（Wang Xiaoyun）さんという中国の山東大学の女性暗号研究者が 2004 年の中旬に発表した論文と、同年末に発表した論文です。

CRYPTO と呼ばれる世界的な暗号学会があるのですが、その 2004年の学会で発表され、話題をさらいました。

"Collisions for Hash Functions MD4, MD5, HAVAL-128 and RIPEMD" by Xiaoyun Wang, Dengguo Feng, Xuejia Lai, Hongbo Yu | August 17, 2004 | PDF @ IACR.ORG

しかし、2004 年の CRYPTO 登壇者一覧を見ても、王（ワン）さんの名前の登壇記録がありません。

登壇者一覧 | CRYPTO 2004 @ IACR

どうやら運営側から「んなこたーない」と論文を却下されたため登壇できなかったそうです。

「それならば」と急遽きゅうきょ生徒を連れてアメリカまで飛んで行き、学会の発表後に行われるランプセッション（持ち時間 15 分程度の発表、学会版 LT）に、飛び込みという形で発表しました。目の前でハッシュ値の衝突を見せたところ驚かれ、話題となったそうです。特に MD4 に関しては、コンピューターなしでも衝突を見つけることができたからです。

ランプセッション・タイムライン 7:35 "Collisions for hash functions MD4, MD5, HAVAL-128 and RIPEMD" | PDF | Crypto 2004 Rump Session Program @ IACR.ORG

しかし、彼女の英語がわかりづらいのと論文の内容が難しく、周りも「なんかすごいことが起きてるっぽい」という状態だったそうです。ところが、同年末から翌年頭（2004 - 2005 年）にかけてさらなる衝撃的な論文を発表します。

SHA-1 の衝突を見つけるアルゴリズムの論文です。

"Finding Collisions in the Full SHA-1" by Xiaoyun Wang, Yiqun Lisa Yin, Hongbo Yu @ IACR.ORG

かねてより SHA-1 の脆弱性を指摘していた暗号・情報セキュリティの巨匠で「シュナイアーの法則」でも知られるブルース・シュナイアー氏が 2005 年 2 月に、この論文を認めたことで、一気に注目のまと・・になります。総当たりで最低でも 2^⁸⁰ 回の処理が必要だったものが、理論上 2^⁶⁹ 回で衝突を発見できるからです。

そして、今度は CRYPTO 学会の方から彼女を招待し、2005 年の CRYPTO に登壇依頼します。ところが、またもや登壇できないということがわかりました。VISA の発行手続きが遅れたからです。

このことは、この論文の解析が難しく検証も遅れていたため、彼女の登壇を心待ちにしていた暗号学者だけでなく、シュナイアー氏も憤慨ふんがいしている記事を書いたくらいの話題性がありました。

その後、時間はかかったものの各種論文も認められ、暗号学会において王（ワン）さんは無事、認知されたそうです。当時の暗号学者たちは、この彼女の論文をパズルを解くようでワクワクしたそうです。

で、結局一番強いアルゴリズムはどれなのよ？

王さんの衝撃論文の発表後、GOOGLE による攻撃（衝突）の検証実証などにより、MD5 や SHA-1 だけでなく SHA-2（SHA-224〜SHA-512 の総称）の見直しが計画されました。

NIST（アメリカ国立標準技術研究所）が次世代 SHA となる SHA-3 のシリーズを作るべく公募したところ、従来の SHA-1 や SHA-2 とは根本的に思想の違う「Keccak」（ケシャック, ケチャック）と呼ばれるアルゴリズムが優勝し SHA-3 に採用されることになりました。そして採用から３年の期間を経て FIPS と呼ばれる連邦情報処理標準に制定されました（FIPS PUB 202）。なお、SHA-3 には SHA3-224〜SHA3-512 だけでなく、可変長で出力される SHAKE128 と SHAKE256 も含まれます。

そのため、2020/10 現在、OS やプログラム言語間で互換性の高いハッシュ・アルゴリズムで一番堅牢なのは「SHA３-512」と言って良いと思います。

SHA-3 の注意点としてリリース時期があります。実は Keccak が採用された後、SHA-3 として FIPS に制定されるまでの間に仕様の変更がありました。そのため、Keccak と SHA-3 では出力結果が異なります。

つまり、ハッシュ関数のライブラリが制定後の更新をしておらず Keccak == SHA-3 の古い仕様のままだと、同じ SHA3 でも異なったアルゴリズムを使っているので出力結果が異なると言うことです。

どちらのアルゴリズムを利用しているかは、実際に「ハッシュ値の例」を元に計算して確認するのが早いと思われます。SHA-3 を利用する場合は以下をテストに含めるか、アプリの初期化時に確認するのがいいでしょう。

Keccakの場合

$ echo -n '' | openssl sha3-224
(stdin)= f71837502ba8e10837bdd8d365adb85591895602fc552b48b7390abd

FIPS_PUB_202準拠の場合

$ echo -n '' | openssl sha3-224
(stdin)= 6b4e03423667dbb73b6e15454f0eb1abd4597f9a1b078e3f5b5a6bc7

参考文献:
- Too Much Crypto @ IACR
- 「Keccak と SHA3 の関係」 @ Qiita
- What is the most secure hashing algorithm? @ Quora

ブルートフォースおまえもか

さて、閑話休題。

つまり、「効率的に衝突する方法は見つかった」ものの、md5 や sha-1 でハッシュ化されたパスワードが流出しても「オリジナルのパスワードが計算で出せるわけではない」ということです。

ところがブロックチェーンの台頭により、やはり md5 や sha-1 は危険とは言えるようです。

と言うのも、ブロックチェーンのプルーフ・オブ・ワーク、俗に言うマイニングと呼ばれる作業が、まさに「ハッシュ値の衝突を探す作業」だからです。（ブロックチェーンの概要は前項の「ハッシュ関数とブロック・チェーン」参照）

マイニングは、基本的に総当たり攻撃の手法を使うわけですが、先の論文を応用すれば他より早くマイニングができることになります。中国のマイナー（マイニングする人）が多いのも、おそらく論文が中国語で読めたからなのかもしれません。たぶん。

同じハッシュ値の改ざん作業でも、ブロックチェーンを崩すよりはマイニングした方が直接的にお金（暗号通貨）を得られるし、そのぶんブロックも堅牢になっていくという良いところ取りなのが、仮想通貨（特にビットコイン）が広まった理由とも言われます。

逆に言うと「その衝突させるノウハウやインフラは悪意を持って改ざんするのにも使える」ということでもあります。

もし、イーサリアム団体が実験で進めている改良版 PoS によりマイニングが不要になった場合、世界中で使われなくなった GPU が溢れることになりかねません。つまり、小銭稼ぎの矛先がハッシュ値のクラッキングに向いてしまう可能性もあります。

そういう意味でも、やはりクリティカルな情報は計算コストが高いとはいえ sha-256 や sha-512、可能なら sha3-512 を使った方が今は安全であるとは言えそうです。

それでも md5 は使いやすく軽量であるため、頻繁に使い捨てされるようなものには依然有用です。やはり、結局のところ機能や特徴をきちんと理解した上で、コストと相談した運用の方針によると思います。

^{🐒 SHA-1 の後続である SHA-2 は、SHA-224, SHA-256, SHA-384, SHA-512, SHA-512/224, SHA-512/256 などの総称です。くどいようですが、SHA-2 は 20 年前に開発されたアルゴリズムです。}

ハッシュ値のベストな提供方法

以上のことから、「セキュリティの強度」や「同一性の確実度」を高めるには、以下の３点を同時に提供するのが効果的とわかりました。

複雑な計算が必要な、長いハッシュ値を提供する（SHA256 など）
異なるアルゴリズムのハッシュ値も一緒に提供する（SHA512 と MD5 など）
データの長さ（ファイル・サイズ）を提供する

OS のイメージ・ダウンロードで SHA-1 と MD5 などの複数ハッシュ値を提供しているのは「SHA-1 ハッシュが使えない人のため」なのかと思っていましたが、どうやらそれだけではないようです。というのも、SHA-1 と MD5 の両方といった複数のアルゴリズムのハッシュ結果を「単一の改ざん」で衝突させるのは難しいからです。

最近は、SHA-1 と MD5 の変わりに sha-256 のハッシュ値と GPG などの署名を同時に提供するのが主流なって来ています。これは異なるアルゴリズムのデータを提供するのと同じ考え方がベースにあります。sha-256 の、より堅牢なハッシュ値と、ハッシュ値を秘密鍵で暗号化した署名を提供することで、さらに難しさを増しています。sha-256 による「データが壊れていないか」の確認と、署名を相手の公開鍵で検証することによって出どころと中身を保証するとを同時に行えるからです。

さて、３番目の「データ・サイズ」ですが、ウィルス本体＋衝突用データ もしくは 改ざんデータ＋衝突用データ と言ったデータが埋め込まれた場合の対策です。と言うのも、オリジナルのデータと同じハッシュ値にさせつつ悪意あるデータを埋め込んで、かつ同じサイズにするには、とても大変な労力（コスト）を必要とするからです。

アルゴリズムの種類と長さ

いまや CSV のように小馬鹿にされる MD5 ですが、SHA-1, SHA-256 などのメジャーどころ以外に、どんなアルゴリズムがあるのか気になりました。

そこで PHP の hash_algos() 関数でサポートしているハッシュ・アルゴリズム一覧を出力したところ「こんなにハッシュ関数（のアルゴリズム）ってあるの？！」とビックリ。

PHP と Python3 のハッシュ・アルゴリズム一覧をオンラインで見る @ paiza.IO

アルゴリズム一覧を見て、「ってか MD2 なんてあったんだ！」と知ったと同時に「MD2 って MD5 と同じ 16 バイト長（128bit= 32 桁の HEX 文字列）なんだ！」と気付きました。

調べてみると英語版の Wikipedia にはハッシュ関数のアルゴリズム一覧があり、その数たるや各々のアルゴリズムの仕組みを把握する気力さえ失せる勢い。（LGTM 頂いたので翻訳を始めたものの途中でバテてしまいました。）

List of Hash Functions @ Wikipedia

そこで、各々のアルゴリズムはどれくらいの長さの値を返すのか調べ、一覧にしてみました。（ついでに速度も）

Multibase（ハッシュ値の n 進数圧縮と規格）

さて、ここまで読んでいただいて「え？16 進数の『数値の文字列・・・』ってことは、64 進数の Base64 とかの n 進数にすればもっと短く表現できるんじゃね？」と思ったかもしれません。

実は私も思いました。「a-zA-Z0-9 に記号を足して 64 文字が ASCII の限界なら漢字を使えばいいじゃない。どうせ UTF-8 なんだし」と。

そして、おふざけで漢字 8118 文字を使って 8118 進数（Base 8118）で表現してみたところ MD5 は 10 桁まで圧縮できました。

$ php ./sample.php
Number of characters:	8118
Original String:	This is a sample string to be hashed.
Pure MD5 hashed string:	baad33e1e97f316b9750c27c86bf64d6
Multibyte base encoded:	䙔倁屩劷䋾彨䏔䂌䤘剒

オンラインで 8118 進数のハッシュ値を見る @ paiza.IO

しかし、薔薇や檸檬どころか醤油すら漢字で書けるか微妙な私には使い物になりませんでした。特に 8118 進数に使った文字も共通ではない（適当に選んだ）ためです。

ところが、同じようなことを考える人はいるもので「Base N（N 進数）で使われる文字を制定しよう」という動きがあります。すでに Base64 に関してはインターネットの制定団体である IETF が RFC-4648 で制定したものがありますが、この概念をさらに拡張したものです。

具体的には、ハッシュ値の頭に識別コードを加えるという仕様です。このコードにより、どの文字を使ってエンコードされたのか（何進数のハッシュなのか）がわかるので、デコードできる（任意の進数の数値に戻せる）ようになります。

例えば、以下のハッシュ値を見せられた場合、コメント（#）がなければデコード、つまり文字列から数値に戻して使うことができなくなります。

4D756C74696261736520697320617765736F6D6521205C6F2F # base16 (hex)
JV2WY5DJMJQXGZJANFZSAYLXMVZW63LFEEQFY3ZP           # base32
3IY8QKL64VUGCX009XWUHKF6GBBTS3TVRXFRA5R            # base36
YAjKoNbau5KiqmHPmSxYCvn66dA1vLmwbt                 # base58
TXVsdGliYXNlIGlzIGF3ZXNvbWUhIFxvLw==               # base64

これは "1234567" という文字列の数値を渡された場合に、「何進数かわからない」と考えればピンとくるかもしれません。8 進数以上の可能性をすべて含んでいるためです。

そこで頭に 1 文字のプレフィックス（接頭辞）を加えて、それを識別子として使います。（上記と見比べてみてください）

F4D756C74696261736520697320617765736F6D6521205C6F2F # base16 F
BJV2WY5DJMJQXGZJANFZSAYLXMVZW63LFEEQFY3ZP           # base32 B
K3IY8QKL64VUGCX009XWUHKF6GBBTS3TVRXFRA5R            # base36 K
zYAjKoNbau5KiqmHPmSxYCvn66dA1vLmwbt                 # base58 z
MTXVsdGliYXNlIGlzIGF3ZXNvbWUhIFxvLw==               # base64 M

感覚として 16 進数の場合は 0x、10 進数の場合は 0d、2 進数の場合は 0b と付けるのと似ています。

このような仕様を「Multibase プロトコル」と呼んでいます。2021/07/16 現在、制定および検討されているものは以下の通りです。

Multibase（2021/07/16）

encoding,          code, description,                                              status
identity,          0x00, 8-bit binary (encoder and decoder keeps data unmodified), default
base2,             0,    binary (01010101),                                        candidate
base8,             7,    octal,                                                    draft
base10,            9,    decimal,                                                  draft
base16,            f,    hexadecimal,                                              default
base16upper,       F,    hexadecimal,                                              default
base32hex,         v,    rfc4648 case-insensitive - no padding - highest char,     candidate
base32hexupper,    V,    rfc4648 case-insensitive - no padding - highest char,     candidate
base32hexpad,      t,    rfc4648 case-insensitive - with padding,                  candidate
base32hexpadupper, T,    rfc4648 case-insensitive - with padding,                  candidate
base32,            b,    rfc4648 case-insensitive - no padding,                    default
base32upper,       B,    rfc4648 case-insensitive - no padding,                    default
base32pad,         c,    rfc4648 case-insensitive - with padding,                  candidate
base32padupper,    C,    rfc4648 case-insensitive - with padding,                  candidate
base32z,           h,    z-base-32 (used by Tahoe-LAFS),                           draft
base36,            k,    base36 [0-9a-z] case-insensitive - no padding,            draft
base36upper,       K,    base36 [0-9a-z] case-insensitive - no padding,            draft
base58btc,         z,    base58 bitcoin,                                           default
base58flickr,      Z,    base58 flicker,                                           candidate
base64,            m,    rfc4648 no padding,                                       default
base64pad,         M,    rfc4648 with padding - MIME encoding,                     candidate
base64url,         u,    rfc4648 no padding,                                       default
base64urlpad,      U,    rfc4648 with padding,                                     default
proquint,          p,    PRO-QUINT https://arxiv.org/html/0901.4016,               draft

Multibase | Multiformats @ GitHub

「（え？比較に使うなら関係ないじゃん。むしろ 1 文字長くなってるし）」と感じるかもしれません。

この規格の利点は、使用していたハッシュアルゴリズムに脆弱性が発見された場合、バージョンアップの際に互換性を確保できることです。つまり、頭の数文字を見るだけで、「アルゴリズム」「ハッシュの長さ」「エンコードの種類」がわかるようになるのです。

もう少し具体的に行きましょう。

例えば、"multihash" という文字列を SHA2-256 のアルゴリズムを使ってハッシュ化した値の場合は 16 進数で以下になります。

"multihash"をSHA2-256でハッシュ化した16進数の値

9cbc07c3f991725836a3aa2a581ca2029198aa420b9d99bc0e131d9f3e2cbe47

この場合、16 進数であることを示すために f を頭につけます。上記対応表に照らし合わせると 16 進数の小文字の場合は f だからです。

16進数小文字のハッシュ値である

f9cbc07c3f991725836a3aa2a581ca2029198aa420b9d99bc0e131d9f3e2cbe47

しかし、これだけではどのアルゴリズムを使ったハッシュ値か、わかりません。

そこで、SHA2-256 のアルゴリズムを使った場合は A を最初に付けるというル俺様ルールを設けたとします。その場合、最終的に以下のようになります。

16進数小文字のSHA2-256ハッシュ値である

Af9cbc07c3f991725836a3aa2a581ca2029198aa420b9d99bc0e131d9f3e2cbe47

「（俺様ルールて。そんな実装で大丈夫か？）」と思ったあなた。もぅ、お分かりでしょう。「神は言っている、アルゴリズムの種類も制定して欲しい」と。

はい、同じ団体が「Multihash」という規格を制定しています。

Multihash @ Multiformats

基本的に以下のような TLV（type-length-value）と呼ばれるフォーマットになっています。

<ハッシュアルゴリズムの種類><データのバイト数><データ（ハッシュ値）>
- 8 ビット（2バイト）の符号なし整数によるアルゴリズム・コード
  - 8 ビット（2バイト）の符号なし整数によるデータのバイト数（ハッシュ値の頭 n 桁だけ渡される場合があるため）
    - データ（ハッシュ値）
122041dd7b6443542e75701aa98a0c235951a28a0d851b11564d20022ab11d2589a8
- SHA2-256
  - 32 文字（=0x20）
    - ハッシュデータ 41dd7b6443542e75701aa98a0c235951a28a0d851b11564d20022ab11d2589a8

実は、先述のビットコインのトークンや IPFS の CID は、ハッシュ値のフォーマットに Multibase と Multihash を使っています。

Content addressing and CIDs @ docs.ipfs.io

長さを知ったところで何？

ですよねー。実は、私は SQLite3² の INTEGER PRIMARY KEY フェチなのです。

さら・・で SQL 文も書けないくせに、「SQLite3」と聞かれれば「主キー♥️」と答えるくらいです。

これは、SQLite3 の場合は DB をキー検索する際に「DB の PRIMARY キー（主キー）を INTEGER 型にすると最もパフォーマンスが良い」というのを盲信しとるのです。（INT 型でなく INTEGER 型の場合に限る）

元々 SQLite3 では rowid で検索するのが一番速いとされます。rowid とは、SQLite では行番号のことです。DB に行（レコード）が作成されると 64 bit/8 byte（HEX 値で max 16桁）の行 ID が自動で割り振られます。

Searching for a record with a specific rowid, or for all records with rowids within a specified range is around twice as fast as a similar search made by specifying any other PRIMARY KEY or indexed value.
^{（ROWIDs and the INTEGER PRIMARY KEY | SQL As Understood By SQLite @ SQLite.org より）}

特定の rowid を持つレコードの検索や、指定した範囲内の rowid を持つすべてのレコードを検索する場合、PRIMARY KEY やインデックス値を指定して同様の検索を行う場合に比べて、約 2 倍の速度で検索することができます。（筆者訳）

この時、テーブルの主キーが rowid と同じであれば、主キーでも同じ速度が得られるのです。

厳密には、テーブル作成時に主キーの列を INTEGER PRIMARY KEY で定義し、テーブルが複数の主キーを持たない場合に限ります。

というのも、テーブルが 1 つだけ主キーを持ち、INTEGER PRIMARY KEY で宣言されると、各行の主キーが rowid のエイリアスとなる SQLite3 の仕様が使えるのです（この時 INTEGER PRIMARY KEY でなく INT PRIMARY KEY と INT で宣言するとダメなので注意）。

If a table has the primary key that consists of one column, and that column defined as INTEGER, exactly INTEGER in any cases, such as, INTEGER, integer, etc., then this primary key column becomes an alias for the rowid column.

表（テーブル）の主キーが１つの列で構成され、かつその主キーが大文字・小文字関係なく INTEGER（INTEGER, integer, INTteger, etc.）と定義されていた場合、この主キーは rowid 列の_エイリアス_になります。（筆者訳）

SQLite Primary Key @ SQLiteTutorial.net
SQLite Create Table @ SQLiteTutorial.net

主キーが `rowid` のエイリアスになるサンプル

実際に INT で宣言したテーブルと INTEGER で宣言したテーブルの SQLite3 内のデータ構造の違いを確認してみたいと思います。

SQLite3 自身の挙動であるため、プログラム言語に依存しない証拠に bash で書いてみたいと思います。sh zsh どのシェルでも大丈夫だと思います。

テーブル作成の SQL 文は CREATE TABLE [テーブル名]([テーブル構成]) です。SQL のコマンドは、大文字・小文字は関係ありません。（CREATE も create も同じ）

まず、主キー名は「myID」とし、主キーの宣言には PRIMARY KEY を指定します。

そして、主キーの型を INT で宣言したテーブル名を table1、INTEGER で宣言したテーブルを table2 とします。table1 が従来のテーブル、table2 が倍速のテーブルです。

また、ポカヨケとして、オプションの NOT NULL で「空の値の myID は許さない」ことにし、挿入するデータは両テーブル同じものとしてみたいと思います。

なお、挿入順を見るために myID の値をわざと降・順にしていることに注意してください。（SQLite3 v3.22.0）

#!/bin/bash

name_db='sample.db'

# Create table 1 and 2 and insert same data
sqlite3 $name_db <<'HEREDOC'
  create table table1(myID INT not null primary key, myName Varchar);
  insert into  table1 values(100, "First  value with ID 100");
  insert into  table1 values(10,  "Second value with ID 10 ");
  insert into  table1 values(1,   "Third  value with ID 1  ");

  create table table2(myID INTEGER not null primary key, myName Varchar);
  insert into  table2 values(100, "First  value with ID 100");
  insert into  table2 values(10,  "Second value with ID 10 ");
  insert into  table2 values(1,   "Third  value with ID 1  ");
HEREDOC
echo '- DB created with sample.'

次に、DB の中身を確認してみます。SQL 文 select rowid, * [テーブル名] で rowid の表示および全てのデータを選択しています。

まずは、主キーが rowid のエイリアスではない table1 です。

table1の中身確認

# .header on と .mode column は見栄えを整える SQLite3 コマンドです
echo '- Table1'
sqlite3 $name_db <<'HEREDOC'
.header on
.mode column
  select rowid, * from table1;
HEREDOC

出力結果（１列目がrowid）

- Table1
rowid       myID        myName
----------  ----------  ------------------------
1           100         First  value with ID 100
2           10          Second value with ID 10
3           1           Third  value with ID 1

rowid 順に並んでおり、rowid と myID の値が同じでないことを確認してください。

このテーブル構成の場合、myID で myName を検索すると、まずは myID と rowid を紐づけるために自動作成されるハッシュテーブルを検索して該当する rowid を見つけます。

そして、見つけた rowid から該当する myName の値を探し、その値を返します。

つまり myID → rowid → myName とワンクッション入ることになります（これ自体は RDB として正しい動きで、連想配列なども同じ仕組みで値を探します）。

それでは次に、rowid が主キーのエイリアスになっている table2 です。倍速の方のテーブルです。

table2の中身確認

echo '- Table2'
sqlite3 $name_db <<'HEREDOC'
.header on
.mode column
  select rowid, * from table2;
HEREDOC

出力結果（１列目がmyID）

- Table2
myID        myID        myName
----------  ----------  ------------------------
1           1           Third  value with ID 1
10          10          Second value with ID 10
100         100         First  value with ID 100

SQL 文で select rowid, * としているのに rowid が myID と同じ（エイリアス）であること、そして１列目の myID 順に並んでいることを確認してください。（DB の登録順は 100→10→1）

このテーブル構成の場合、myID で myName を検索すると、直接 rowid（のエイリアスの myID）の myName を返します。例えば、特定の rowid で myName の値を取得したい場合は以下の通り。

"rowid"が"100"の"myName"の値を"table2"から取得するSQL文の例

select myName from table2 where rowid = 100;

オンラインで動作をみる @ paiza.IO

`rowid` が主キー

この、主キーが rowid のエイリアスになる仕様により「主キー名」から「rowid」への変換ステップが省略され、テーブルの主キーが rowid と同じ扱いになるので速い、という塩梅です。

元々はバグだったそうなのですが下位互換のため残され、仕様となったそうです。

そして、主キー（PRIMARY KEY）が rowid と同じということは、任意の rowid を振れるということでもあります。

となると、SQLite3 で扱えるキー（rowid）の最大長である 8 バイトの数値（64 ビット。文字でいうと 16 文字の HEX 文字列）をいかに作るかが問題になります。

Except for WITHOUT ROWID tables, all rows within SQLite tables have a 64-bit signed integer key that uniquely identifies the row within its table. This integer is usually called the "rowid".

^{（ROWIDs and the INTEGER PRIMARY KEY | CREATE TABLE @ SQLite.org より）}

【筆者訳】
WITHOUT ROWID で定義されたテーブルを除いて、SQLite のテーブル内のすべての行には、テーブル内の行を一意に識別する 64 ビットの符号付き整数キーを持ちます。この整数は通常「rowid」と呼ばれます。
_{^{（筆者注: 64 ビットの符号付き整数とは -9,223,372,036,854,775,808 〜 9,223,372,036,854,775,807 の範囲の整数。HEX の場合は -8000000000000000 7fffffffffffffff。「符号付き」というのは、バイナリ・データの最初のビットが「マイナス値かプラス値かを示す符号」として使われている値のこと。）}}

やはり、王道の自動連番が一番楽で、キーの衝突もなく効率的です。基本設計がしっかりしていれば、これが一番だと思います。

しかし、（私の）ユーザにとっては変なバイアスがかかる忖度が発生することがわかりました。

というのも、歴史的事情でデータの ID を DB の主キーと同じにしているというダメちん仕様のため、当然の結果として「情報の ID 番号が時系列に並ぶ」、つまり登録順に並ぶのです。すると（私の）ユーザは無意識に内容の優劣を決めてしまうのです。

「ID が小さい → 古参の情報」「ID が大きい → 新参の情報」といった具合です。そのため、（私のようなオッチャン層は特に） ID が小さい方が質が良い・有益であると思い込んでしまうのです。観測すると、実は打ちやすい・覚えやすいだけで、番号に質は無関係だったのですが。

かといって、対オッチャン対策のためにランダムな ID の対応表を別途作るのも面倒なのです。また、すでに現行データの ID は周知されているので入れ替えは容易ではありません。

そこで、近々起こりうるであろうデータの棚卸しに備えてハッシュ関数を使って ID を固定長にできないかと模索をはじめました。

Hash now, don't you cry

ここからは、SQLite3 の主キーが rowid と同等の場合に、主キーの最大長である 8 バイトの数値をハッシュ関数でいかに作成したかの具体的な内容になります。

PHP の場合、fnv1 系（fnv164 もしくは fnv1a64）のアルゴリズム一発で 8 バイト（64 bit, 16 桁の HEX 文字列）のハッシュが作れます。

そのため、古いキーを単純にハッシュ化して再登録すれば楽に移行できます。しかも、速い。

$key_prime_new = hash('fnv164', $key_prime_old);

ところが、いくつか問題があるのです。

現在、この記事で話題にしている「要オッチャン対策 DB」が扱っているデータは登録後の変更はありません。いや、むしろ変更してはいけないものなのです。

ところが自由度の高い設計であるためか、自分の独断と都合により何故か勝手に値を変えちゃう一部の層（上流やオッチャン層）がありました。その層に弱い上司からコッソリと指示を受けるたび、バックアップから元に戻す作業のイタチごっこが定期的に発生していました。

これではいつかは盛大なポカをやりかねません。仕組みとしてのポカよけが必要と感じ、もう少し工夫をしたいなと思いました。

昨今の行政の改ざん問題でも提案されている文書のハッシュ化を ID として取り入れたいと考えたのです。

CAS な DB と呼ばれようとも

文書のハッシュ値を ID にする、つまりイメージではこういうことです。

// 旧IDでデータ取得
$value = fetchValueFromDB($key_prime_old);
// データ → ハッシュ化（16進）→ 10進 → 整数
$key_prime_new = (integer) hexdec(hash('fnv164', $value));

このような、コンテンツのハッシュ値を ID にする DB を「Content-addressable storage（CAS）」と言います。git や IPFS なども CAS の一種です。

先の「要オッチャン対策 DB」は「ユーザが測定したデータの値と同じ値のものを DB から探し、関連情報（ヒットした行のデータ）を返す」用途に使われています。

ピピピッピッと打つか、ピッとバーコードを読み込むと、ポッとデータが表示されるシンプルなものです。

つまり、ユーザ側（クライアント側）で測定したデータをハッシュ化したものをキーとして DB（サーバー側）に渡し、DB は受け取ったキーを検索すれば速度改善・改ざん防止・オッチャン対策の良いとこ取りになります。DB もシンプルに実装・構成できます。

ここで、もし１つ前の登録データのキーもハッシュ化してフィールドに内包（列を追加）すれば、ブロックチェーンに近い考え方になりますよね。そもそも SQLite なので、同期されたデータは各クライアント（ユーザ）のローカルにありますし。

さて、この方法でテストしたところ、今のところ１億件ちょっとの既存データで衝突もなく問題なさそうなのですが、１つのアルゴリズムに依存したくないという気持ちもありました。そう、ハッシュ値の衝突が怖いのです。

そもそも、この程度（10 年で 1〜2 億件程度）のデータ量であれば、SQLite3 の 1844京6744兆737億件以上も使える 8 バイト（64ビット）のキーをそのまま使うのはもったいないのです。大は小を兼ねるとは言え、貸し倉庫クラスなのにデズニーランド・クラスのスペースを使うようなものです。

十分な年数に耐えつつ、衝突に関しては鳩の巣原理（鳩の数より巣箱の数が少ないと、１つ以上の巣箱で衝突が起きる原理）は少なくとも網羅できるバイトの長さを検討した結果、最長 4 バイト長（= 42.9 億個）のキーとしました。

そして、先の「衝突しても別のアルゴリズムだと衝突しない（可能性が高い）」屁理屈を取り入れて、「4 バイトの A 型ハッシュ値 + 4 バイトの B 型ハッシュ値 = 8 バイトのキー」を作ってみたいと思いました。

具体的には 4 バイト長のハッシュ・アルゴリズムである crc32 と fnv132 の２つをあわせて以下のような Primeキーの算出を考えました。

$key_prime_hex = hash('fnv132', $value) . hash('crc32', $value);

厳密に言うと CRC-32 はハッシュではなくチェックサムなのですが、計算コストをケチってしまいました。これが後に懸念を産むことになります。

crc32 @ Wikipedia（日本語）
fnv-1 32 @ Wikipedia（英語）

先の fnv-1 64（8 バイト長のアルゴリズム）単体と比べて２倍くらい速くなるのですが、移行のための一括登録のデータ量が 500 万件を越えたあたりから、むしろ遅くなりました。アルゴリズムの組み合わせにもよると思いますが、アルゴリズムによっては初期化に原因がありそうです。

しかし、本番データは一括 INSERT させる予定です。つまり、一旦 DB をダンプ出力して主キーを整形しておき、データを新規 DB に一括で INSERT させる感じです。

また、実際の用途では新規登録時の速度はさほど必要とされておらず、登録頻度も高くありません。むしろ登録より日々の引き出し時の速度が速くなったことのほうが改善感があって良いと思います。

手元の２億件弱のサンプル・データで、このアルゴリズムの組み合わせで衝突は発生しませんでした。しかし、アルゴリズムの仕様を調べていくうちに確信が持てなくなりました。

非暗号学的ハッシュに悩む

CRC はチェックサムなのでデータが連番の場合に弱いのと、fnv-1 系（Fowler–Noll–Vo）のアルゴリズムは非暗号化型ハッシュ、つまり暗号学的ハッシュ関数ではないため、スティッキーステートと呼ばれる問題を孕んでいます。（暗号学的ハッシュについては上部「ハッシュ関数の基本と特徴」参照）

Sticky State – Being an iterative hash based primarily on multiplication and XOR, the algorithm is sensitive to the number zero. Specifically, if the hash value were to become zero at any point during calculation, and the next byte hashed were also all zeroes, the hash would not change. This makes colliding messages trivial to create given a message that results in a hash value of zero at some point in its calculation. Additional operations, such as the addition of a third constant prime on each step, can mitigate this but may have detrimental effects on avalanche effect or random distribution of hash values.
^{（Non-cryptographic hash | Fowler–Noll–Vo hash function @ Wikipedia より）}

【筆者訳】
スティッキーステート – Fowler–Noll–Vo 関数は、主に乗算と XOR に基づく反復ハッシュであるため、このアルゴリズムは数値ゼロに敏感です。具体的には、ハッシュ値が計算中のいずれかの時点でゼロになり、続くバイトのハッシュがすべてゼロであった場合、ハッシュは変化しません。これにより、計算のある時点でハッシュ値がゼロになるメッセージが与えられた場合、衝突するメッセージを簡単に作成できます。各ステップで第３の素数を定数として追加するなどの操作で、これを軽減できますが、アバランシェ効果またはハッシュ値のランダム分布に有害な影響を与える可能性があります。

筆者も良く理解出来ていないのですが、fnv-1 は主にハッシュテーブルやチェックサムで使用するために速度を優先して設計されたハッシュ関数として開発されたため、暗号学的ハッシュ関数と比較してランダム性に欠けるということのようです。つまり fnv-1 も CRC と似た連番に弱い問題を持っていたのです。

この DB の仕組みも、ある種のハッシュテーブルと似てはいるものの、この CRC と fnv-1 の組み合わせではコンテンツの高速な確認には使えても ID としては厳しい予感がします。なんたるジレンマ。

となると、より分散性の高いアルゴリズムである SHA などの暗号学的ハッシュの一部を使った方が良いことがわかりました。

問題はコスト（速度）です。

しかし、記事上部の各アルゴリズムの測定速度を見てもわかるように PHP7 の場合 100 万回ぶん回して 0.n 秒の差です。PHP8 だとさらに数倍速くなるので、微々たる差だと思います。

そのため、CRC-32 や fnv-1 を使うよりは Git のコミット ID のように SHA-256, SHA-512 や SHA3-512 などのハッシュ値の頭 4 バイトを使うのがよろしいかと思われます。

^{🐒 私はそうすることにしました。この仕組みが認められるころには PHP8 もリリースされると思うし。いつか Wikipedia のデータをぶっ込んで検証してみたいと思います。どうも、変更できない仕組みが一部で都合が悪いらしく採用されなさげ、ってかその仕事も辞めちゃったので実装することもなさげです。たくさんの「❤︎」をいただけたので模索してよかったと思います。}

イメージとしてはこんな感じ

$len   = 8; //4バイトのHEX文字列長
$value = fetchValueFromDB($key_prime_old);
$hash1 = substr(hash('sha3-512', $value), 0, $len);
$hash2 = substr(hash('sha512', $value), 0, $len);

// 8バイトの主キー
$key_prine_new = (integer) hexdec($hash1 . $hash2); // 実際には ± の符号確認のため $hash1 の一番左の文字をゴニョゴニョしてます

オンラインで動作を見る @ paiza.IO

（え？「もう、KVS でいいじゃん」って？ま、まぁ…ねぇ、、、枯れた技術を好むのも歳なんですかねぇ）

RFC-1146 TCP Alternate Checksum Options @ ietf.org ↩
SQLite3とは、著作権の発生しないオープンソースのデータベース管理システムです。名前からわかるように SQL の構文でデータにアクセスでき、リレーショナル・データベース（RDBMS）の１つです。
　特徴としては「本体も動作も軽量である」ことと「サーバーを立てずに使えること」があります。サーバー型でないため、複数ユーザーや複数アプリからの同時利用には向かないのですが、アプリごとにデータを保存する場合に威力を発揮するタイプです。
　モバイル・アプリやゲームなどのダウンロードやキャッシュ・データであったり、macOS の場合は標準でインストールされており、Spotlight などの検索用の DB としても使われています。（sqlite3 -help で確認可能）
　リアルタイムに激しく変動するデータでない場合、アプリ起動時に本艦となるサーバーからデータ・ベースをダウンロードしてローカルに保存することで、ネットワークのトラフィックを減らしたり、オフラインで利用させたり、レスポンスの向上に使われたりする便利なプログラムです。
関連リンク：SQLite @ Wikipedia 日本語 ↩

487

398

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up