※今回の内容はYouTube動画でもご紹介しています。
相関係数とは?
「相関係数」とは、2種類の変数間の(線形)関係の強さを数値で示す指標
です。
たとえば、「売上と広告費」や「温度と製品の歩留まり率」のように、データ間の関係性を数値として表すことで、データの意味をより客観的かつ説得力のある形で理解できるようになります。
本記事では、この「相関係数」について、基本的な意味や求め方をデータ分析初心者の方にも分かりやすく説明します。
相関関係とピアソンの積率相関係数
前提として、「相関関係」について少し触れておきましょう。
相関関係とは、2種類の連続変数の間にある関係性のことを指します。そして、相関の指標としては、「ピアソンの積率相関係数」が最も一般的に用いられており、記号 r で表されます。
また、相関 係数(以下、ピアソンの積率相関係数のことを指します) r は、−1から1の範囲の値をとり、その値によって関係の強さと方向性を判断します。
• r = +1:完全な正の相関(Xが増えるとYも増える)
• r = −1:完全な負の相関(Xが増えるとYが減る)
• r = 0:線形相関なし(ただし非線形関係が存在する可能性あり)
「相関は線形関係を見るものだ」と言われることがありますが、散布図に回帰直線を引いたときに、データ点がその直線にどれぐらい近いかを反映したものが相関係数なのです。
そして、実務の現場では、相関係数は変数間の初期的な関係性を探るための指標として使われることが多いため、これを理解することはデータ探索を進めるうえでの第一歩になります。
相関係数の求め方と実践例:歩留まり向上へのアプローチ
それでは、相関係数の計算式に基づいて実際に値を求めながら、具体的にどのように課題解決に活かせるのかを見ていきましょう。
【課題】工程条件と歩留まりとの関係性を調べる
ある半導体製造ラインで、特定のロットにおいて歩留まりの低下が頻発していました。
エンジニアは「工程条件にばらつきがあるのではないか」と考え、複数の工程パラメータ(チャンバー温度、ガス流量、圧力)と歩留まり率との関係性を探ることにしました。
■ チャンバー温度と歩留まりの関係
| チャンバー温度 (℃) | 歩留まり (%) |
|---|---|
| 180 | 87 |
| 185 | 86 |
| 190 | 88 |
| 195 | 90 |
| 200 | 89 |
| 205 | 91 |
| 210 | 88 |
| 215 | 91 |
チャンバー温度と歩留まり率という2つの変数の関係性を見るために、相関係数を算出します。
相関係数の計算式:
$$
r = \frac{\sum{(x_i - \bar{x})(y_i - \bar{y})}}{\sqrt{\sum{(x_i - \bar{x})^2} \cdot \sum{(y_i - \bar{y})^2}}}
$$
計算の過程:
$$
x_i:\text{チャンバー温度}、y_i:\text{歩留まり率}
$$
$$
平均: \bar{x} = 197.5、
\bar{y} = 88.75
$$
$$
偏差積和:\sum{(x_i - \bar{x})(y_i - \bar{y})} = 115.0
$$
$$
偏差平方和の平方根:\sqrt{\sum{(x_i - \bar{x})^2}} = 32.4、
\sqrt{\sum{(y_i - \bar{y})^2}} = 4.85
$$
$$
r = \frac{115.0}{32.4 \times 4.85} = \frac{115.0}{157.14}\approx 0.73
$$
解釈: 適度に強い正の相関があり、チャンバー温度の高低が歩留まりに影響を与えている可能性があります。
■ ガス流量と歩留まりの関係
| ガス流量 (sccm) | 歩留まり (%) |
|---|---|
| 45 | 89 |
| 50 | 89 |
| 55 | 89 |
| 60 | 89 |
| 65 | 89 |
| 70 | 91 |
| 75 | 88 |
| 80 | 92 |
計算の過程:
$$
x_i:\text{ガス流量}、y_i:\text{歩留まり率}
$$
$$
平均: \bar{x} = 62.5、
\bar{y} = 89.5
$$
$$
偏差積和:\sum{(x_i - \bar{x})(y_i - \bar{y})} = 55.0
$$
$$
偏差平方和の平方根:\sqrt{\sum{(x_i - \bar{x})^2}} = 32.4、
\sqrt{\sum{(y_i - \bar{y})^2}} = 3.46
$$
$$
r = \frac{55.0}{32.4 \times 3.46} = \frac{55.0}{112.1}\approx 0.49
$$
解釈: 相関はやや弱いものの、正の相関が見られます。
■ 圧力と歩留まりの関係
| 圧力 (Pa) | 歩留まり (%) |
|---|---|
| 10 | 89 |
| 11 | 88 |
| 12 | 87 |
| 13 | 86 |
| 14 | 89 |
| 15 | 91 |
| 16 | 88 |
| 17 | 89 |
計算の過程:
$$
x_i:\text{圧力}、y_i:\text{歩留まり率}
$$
$$
平均: \bar{x} = 13.5、
\bar{y} = 88.38
$$
$$
偏差積和:\sum{(x_i - \bar{x})(y_i - \bar{y})} = 7.5
$$
$$
偏差平方和の平方根:\sqrt{\sum{(x_i - \bar{x})^2}} = 6.48、
\sqrt{\sum{(y_i - \bar{y})^2}} = 3.98
$$
$$
r = \frac{7.5}{6.48 \times 3.98} = \frac{7.5}{25.79}\approx 0.29
$$
解釈: 正の相関が認められるものの、相関は弱いです。
-結果の考察-
今回の3つのパラメータの比較から、チャンバー温度が歩留まりに対して最も強い正の相関を示すことが明らかになりました。
ガス流量や圧力も一定の相関はありますが、どうやら温度管理が歩留まり改善のカギになる可能性がありそうです。
ただ、分析の際、相関係数だけ注目してしまうと誤解が生じることがある
ので注意が必要です。たとえば、曲線関係や極端な外れ値が存在する状況では、算出された相関係数が相関関係を正しく表しているとは限りません。
まとめ:データから関係性を読み解く第一歩としての相関係数
相関係数は、さまざまな業務 — マーケティング、製品開発、顧客満足の分析、経営判断など — において、変数間の関係性の強さを定量的に把握するための基礎指標です。数値で表すことで、感覚や経験に頼らず、客観的な判断に役立ちます。
ただし、相関係数はあくまで「関係」についての指標であり、「原因・結果」を示すものではありません。まずは散布図などで可視化し、相関が確認できれば、予測や原因推定を実施するために回帰分析などへつなげるのが自然な流れです。
つまり、相関係数は「関係性の強さを測る指標」ではありますが、より高度な解析へと連続する「架け橋」の役割を担っていると言えるかもしれません。
業界を問わず、データを使って課題を見つけ、原因を解明し、改善につなげたいすべての方にとって、相関係数の正しい理解と活用は、データドリブンな意思決定を支える出発点と言えるでしょう。
(おまけ)統計ソフトJMPで相関係数を出すには
統計ソフトJMP(ジャンプ)では、相関係数は手計算せずに簡単に算出できます。スクリーン上部の「分析」から「二変量の関係」と進んで散布図を描き、要約統計量を表示させるだけです。
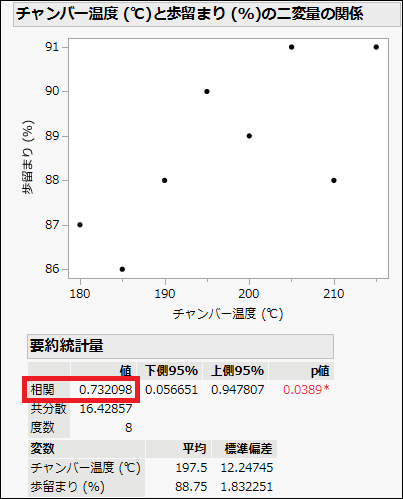
JMPはプログラミング不要で扱いやすい統計ソフトです。まだ試したことがない方は、トライアル版をぜひ試してみてください(自動課金はされません)。
JMP体験版:30日間全機能無料(自動課金はされません)
https://www.jmp.com/ja_jp/download-jmp-free-trial.html?utm_campaign=bl&utm_source=blog&utm_medium=JMPblog
さらに詳しく知りたいときは...
Statistics Knowledge Portal:相関係数
https://www.jmp.com/ja/statistics-knowledge-portal/what-is-correlation/correlation-coefficient
