無から始める Keras のもくじはこちら

前回のおさらい

前回は、手書き数字画像のデータセット MNIST を用い、畳み込みニューラルネットワーク（CNN）で手書き数字認識を行った。

前々回の単純な実装と比較して、高い認識率をあげることができた。

時系列を扱えるニューラルネットワーク

今までは、ある 1 つのデータをニューラルネットワークに入れて、その結果を得ていた。

しかしこれでは時間情報のあるデータを扱うことが難しい。時系列のあるデータにおいては、各時刻のデータとは別に、その時間情報も扱いたい。

ここでは、リカレントニューラルネットワーク（Recurrent Neural Networks）を用いて時間的な構造を持つデータを扱ってみたい。

ちなみに RNN と表記すると Recursive Neural Networks と区別がつかなくなるので、ここではちょっと長いがリカレントニューラルネットワークと書く¹。

リカレントニューラルネットワーク概観

最も単純なものを図にするとこんな感じになる。リカレントニューラルネットワーク自体にはいろいろあるが、このエルマンが提案したものが一番有名らしい²。世の中の図は書いた人の好みでいろいろ省略されるので雰囲気で読み取る能力が必要な気がする。

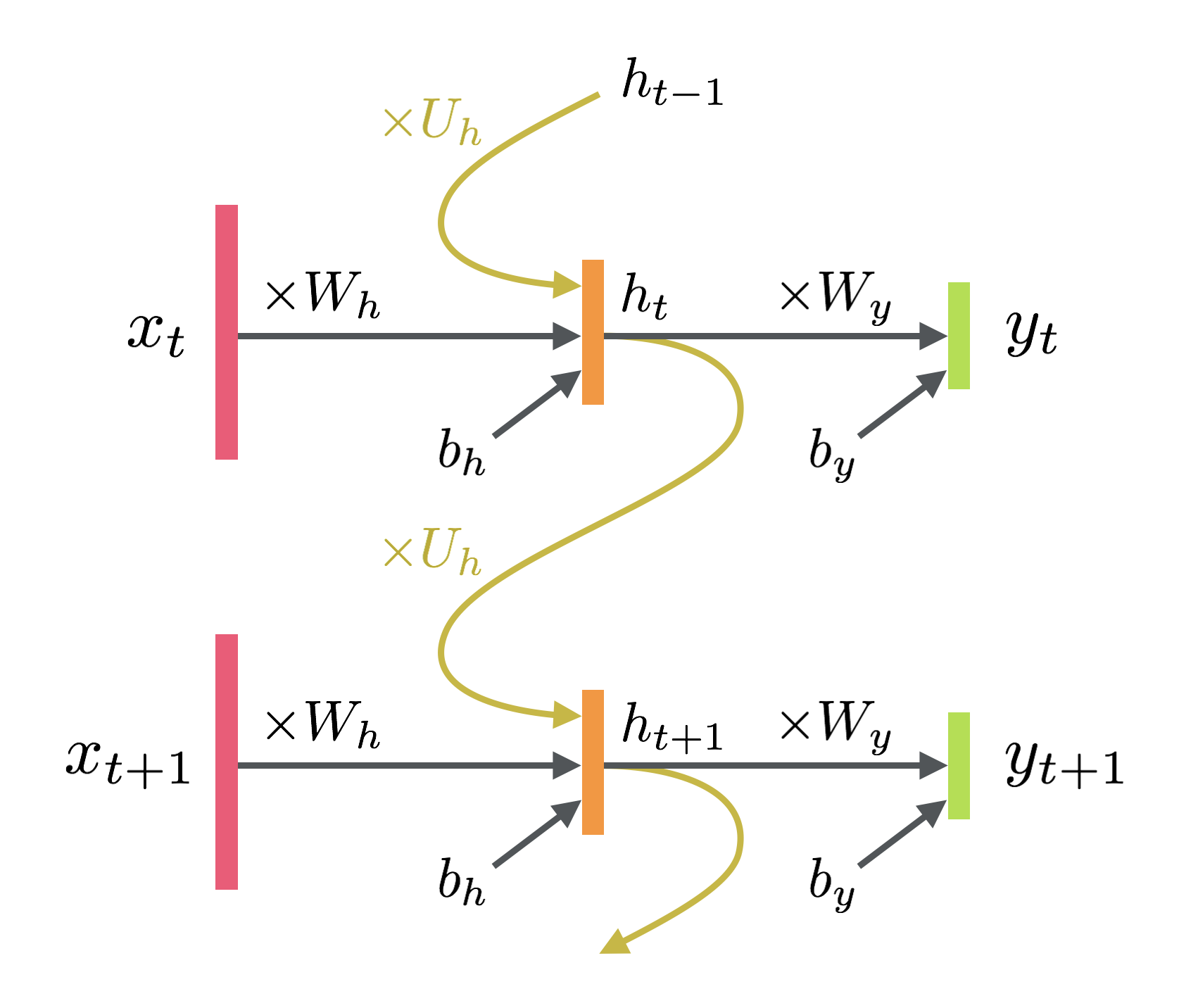
数式で表しておくと次のような感じ。$\sigma$ は活性化関数。

\begin{align}
h_t &= \sigma_h\left(W_h x_t + U_h h_{t-1} + b_h\right) \\
y_t &= \sigma_y\left(W_y h_t + b_y\right)
\end{align}

図の黄色い線によって、時間方向に依存したニューラルネットワークが作れるわけである。

リカレントニューラルネットワークの注意点

上の図だけから把握できないことをかいつまんで。

系列全体から 1 つの答えを出すようにできる

上の図では系列 in 系列 out だったが、系列 in 1 つだけ out もできる（最後以外の出力を無視する）。Keras ではデフォルトが後者になっている。

ただしリカレント層の次にもう一度リカレント層がくる場合は、当然先の層は系列 in 系列 out である必要がある。

可変長はめんどくさい

上の図だけでは系列長が固定じゃなくてもいい感じがするのだが、学習時の効率の問題（過去までネットワークを展開して学習を行う Back Propagation Through Time（BPTT）の適用とか、バッチとか）で系列長を固定したほうがなんだかんだ扱いやすい。

可変長の場合は、バッチサイズを 1 にして 1 系列ごとに学習をするか、事前に 0 などで埋めてしまうという方法をとる。ただバッチサイズが 1 はあまりよくなさそう。

後者は pad_sequences を使うと便利。当然ではあるが、後者のパディングする手法ではパディングされた部分に対する損失関数を 0 にするための処理を行うとよい（参考）。

初期状態

当然漸化式的な実装なので、$t=0$ のときが問題になる。Keras では initial_state という名前で指定できる。指定しない場合にはすべて 0 のベクトル（テンソル）が初期値になる。

実際に組んでみる

ここでは [0,1] と [1,0] を繰り返すだけのデータを出力する、存在価値が無なリカレントニューラルネットワークを作ろう。入力は一様分布のランダム。

データの作成

データを作る。テンソルはデータ方向×系列長さ×次元数とする。データ数は 250、系列長は 100 とした。

import numpy as np

x_train = np.random.rand(250, 100, 1)
y_train = np.tile(np.array([[[0,1],[1,0]]]), (250, 50, 1))

モデルの組み立て

今回はそんなに複雑なモデルは作らない。

ここでは先ほどの図とまったく同じ形の実装をする。1 層目のリカレント層は活性化関数を tanh に、2 層目の結合層は softmax にした。

from keras.models import Sequential
from keras.layers import Dense, SimpleRNN

model = Sequential()
model.add(SimpleRNN(10, activation='tanh', input_shape=(100, 1), return_sequences=True))
model.add(Dense(2, activation='softmax'))

学習せずに動かしてみる

学習しなければぐちゃぐちゃになることを一応確認しておこう。

test = model.predict(np.random.rand(1,100,1))

無なデータが得られる。

わかりにくいので 0 と 1 にしてみよう。

test = (test >= 0.5) * 1
print(test)

溢れ出るランダム感。

学習

この無意味なニューラルネットワークを学習してみる。

エポック数は適当に指定した。完全に過学習させてると思うけど許して。

model.compile('adam', 'binary_crossentropy', metrics=['accuracy'])
model.fit(x_train, y_train, batch_size=10, validation_split=0.05, epochs=15)

テスト

さっきと同じ。

test = (model.predict(np.random.rand(1,100,1)) >= 0.5) * 1

かなりちゃんと動いたと思う。

ちなみに全部ゼロとかでも動く。

test = (model.predict(np.zeros((1,100,1))) >= 0.5) * 1

系列長が可変の場合

層を積むときに系列長を None で指定してやればよい。

model.add(SimpleRNN(10, activation='tanh', input_shape=(None, 1), return_sequences=True))

学習時に渡す配列の形から系列長が同じである要請をうけるため、異なる系列長で学習することは（1 回の fit では）できない。したがって、上で述べたような切る or パディングするの処理が必要になる。

予測時は別個で予測させればよいので細かいことは気にしなくてもよい。

今回のプログラムまとめ

あまりにも存在価値が無だけれど、これが基本になるはず。

import numpy as np
from keras.models import Sequential
from keras.layers import Dense, SimpleRNN

x_train = np.random.rand(250, 100, 1)
y_train = np.tile(np.array([[[0,1],[1,0]]]), (250, 50, 1))

model = Sequential()
model.add(SimpleRNN(10, activation='tanh', input_shape=(100, 1), return_sequences=True))
model.add(Dense(2, activation='softmax'))

model.compile('adam', 'binary_crossentropy', metrics=['accuracy'])
model.fit(x_train, y_train, batch_size=10, validation_split=0.05, epochs=15)

test = (model.predict(np.random.rand(1,100,1)) >= 0.5) * 1
print(test)

次回もなにするか考えてません。なんかもうちょっとマシなリカレントネットワークを扱ってみようかしら。

日本語だと再帰型ニューラルネットワークということもあるが、どちらかというと
recursive のほうが再帰だし微妙。適切な日本語訳がなさそうなのでこうした。 ↩
Jeffrey L. Elman. Finding Structure in Time. Cognitive Science, 14 (2), pp. 179–211, 1990. ↩

無から始めるKeras 第7回