DeepSeek-R1でテキストクラスタリングしてみる

はじめに

この記事では、LLMを用いてテキストデータを2次元に投影し、クラスタリングを行います。
LLM: DeepSeek-R1-Distill-Qwen-14B（Paper, Hugging Face, Kaggle Models）
テキストデータ: 数学の公式名（"Pythagorean Theorem", "Quadratic Formula", "Binomial Theorem", "Fundamental Theorem of Calculus", "Euler's Formula", etc.）
クラスタリング手法: HDBSCAN（Paper, GitHub, PyPI）

昨年一人アドカレを完走した際に、25記事のタイトルをLLMでクラスタリングしてみました。昨年の記事のLLMとしては、Llama-3.1-8Bを用いました。こちらのコードを参考にしています。

実装

import numpy as np
import pandas as pd
import torch
from transformers import AutoTokenizer, AutoModel 
import umap.umap_ as umap
import hdbscan
import plotly.graph_objs as go

math_formulas = [
    "Pythagorean Theorem",              # ピタゴラスの定理
    "Quadratic Formula",                # 二次方程式の解の公式
    "Binomial Theorem",                 # 二項定理
    "Fundamental Theorem of Calculus",  # 微積分の基本定理
    "Euler's Formula",                  # オイラーの公式
    "Law of Cosines",                   # 余弦定理
    "Law of Sines",                     # 正弦定理
    "L'Hôpital's Rule",                 # ロピタルの定理
    "Taylor Series Expansion",          # テイラー展開
    "Fourier Transform",                # フーリエ変換
    "Cauchy-Schwarz Inequality",        # コーシー・シュワルツの不等式
    "Bayes' Theorem",                   # ベイズの定理
    "Central Limit Theorem",            # 中心極限定理
    "Green's Theorem",                  # グリーンの定理
    "Stokes' Theorem",                  # ストークスの定理
    "Divergence Theorem",               # 発散定理（ガウスの定理）
    "De Moivre's Formula",              # ド・モアブルの公式
    "Vieta's Formulas",                 # ヴィエタの公式
    "Heron's Formula",                  # ヘロンの公式
    "Newton's Method",                  # ニュートン法
    "Chain Rule",                       # 連鎖律（合成関数の微分）
    "Product Rule",                     # 積の微分法則
    "Quotient Rule",                    # 商の微分法則
    "Integration by Parts",             # 部分積分法
    "Stirling's Approximation",         # スターリングの近似
    "Leibniz Rule",                     # ライプニッツの法則
    "Mean Value Theorem",               # 平均値の定理
    "Intermediate Value Theorem",       # 中間値の定理
    "Squeeze Theorem",                  # はさみうちの定理
    "Laplace Transform"                 # ラプラス変換
]

# ================ LLMモデルの準備 ================
# モデルとトークナイザの読み込み
model_name = "deepseek-ai/DeepSeek-R1-Distill-Qwen-14B"
tokenizer = AutoTokenizer.from_pretrained(model_name)
model = AutoModel.from_pretrained(model_name, torch_dtype="half", device_map="auto")

def get_embedding(text: str) -> np.ndarray:
    inputs = tokenizer(text, return_tensors="pt")
    with torch.no_grad():
        outputs = model(**inputs)
    # 平均プーリング
    embedding = outputs.last_hidden_state.mean(dim=1).squeeze().numpy()
    return embedding

# 埋め込み取得
X = np.array([get_embedding(title) for title in math_formulas])

# ================ UMAPによる次元削減 ================
umap_reducer = umap.UMAP(n_neighbors=5, min_dist=0.1, n_components=2, random_state=42)
X_2d = umap_reducer.fit_transform(X)

# ================ クラスタリング ================
# HDBSCANでクラスタリング（自動で適切なクラスタ数を抽出）
clusterer = hdbscan.HDBSCAN(min_cluster_size=2, metric='euclidean', cluster_selection_epsilon=0.1)
labels = clusterer.fit_predict(X_2d)
# ノイズ(-1)はクラスタ外として扱われる

# ================ 可視化 ================
def visualize_2d_data(points, labels, texts, title="UMAP + HDBSCAN Clustering"):
    unique_labels = np.unique(labels)
    color_map = {}
    for lbl in unique_labels:
        if lbl == -1:
            color_map[lbl] = "rgba(128,128,128,0.8)"
        else:
            color_map[lbl] = f"hsl({(lbl * 60) % 360}, 70%, 50%)"

    data_traces = []
    for lbl in unique_labels:
        mask = (labels == lbl)
        data_traces.append(go.Scatter(
            x=points[mask, 0], 
            y=points[mask, 1],
            mode='markers+text',  
            text=[texts[i] for i in np.where(mask)[0]],
            textposition='top center',  
            textfont=dict(size=8),       
            marker=dict(color=color_map[lbl], size=10),
            name=f"Cluster {lbl}" if lbl != -1 else "Noise"
        ))
    fig = go.Figure(data=data_traces)
    fig.update_layout(
        title=title,
        xaxis_title='UMAP Component 1',
        yaxis_title='UMAP Component 2',
        showlegend=True,
        hovermode='closest'
    )
    fig.show()

visualize_2d_data(X_2d, labels, math_formulas, title="DeepSeek-R1 for Clustering in Text ")

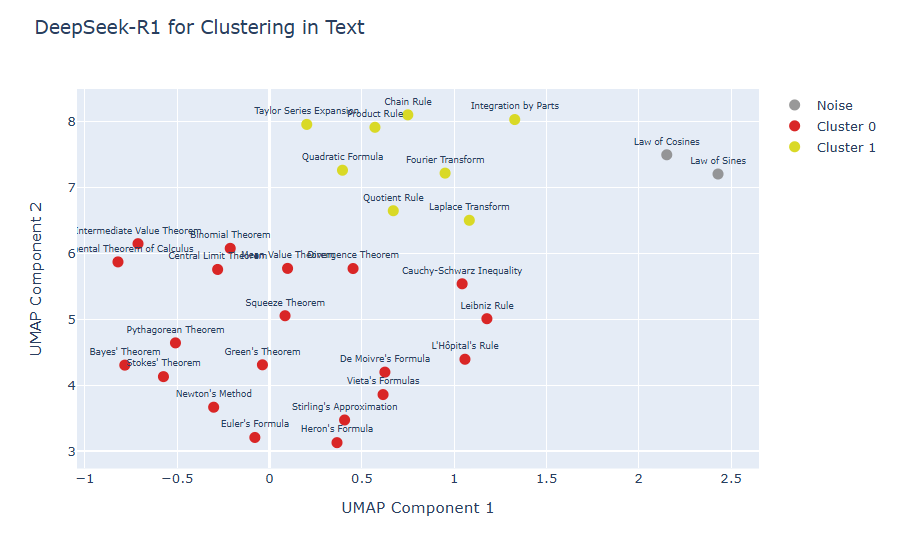
クラスタリング可視化結果

まとめ

クラスタリング結果は、Cluster 0に微積分の基本定理や平均値の定理、ピタゴラスの定理など、基礎解析学および古典的な定理が集まり、Cluster 1へはChain Rule（連鎖律）、Product Rule（積の微分法則）、Integration by Parts（部分積分法）など具体的な微分・積分の計算規則や手法が分離しました。
DeepSeek-R1 を使った embedding → UMAP → HDBSCAN により、数学公式名の集合を 意味的に近い公式群でまとまりを作る ことが多少可能であるように見えました。ただし、DeepSeek-R1 は本来「生成／推論用 LLM」であって、embedding 特化モデルではないです。そのため、埋め込みの信頼性や普遍性には限界があります。

本記事で使用したソースコードは、Kaggle環境で動作を確認しています。