電子回路では抵抗器を合成した合成抵抗を求める事が良くあります。Mathematicaでグラフ理論を使って合成抵抗を求めてみます。
1 直並列回路の合成抵抗
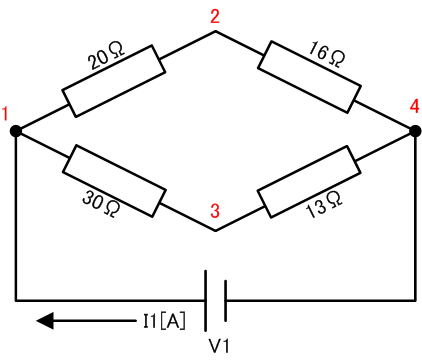
上図の様な直並列回路の合成抵抗を求めてみます。赤字は頂点を示します。
先ずは回路の接続をグラフで表します。
Clear["Global`*"];
g1 = Graph[Range[4],
{1 -> 2, 1 -> 3, 2 -> 4, 3 -> 4, 4 -> 1}];
次にコンダクタンス(抵抗の逆数)の行列を作ります。回路図から頂点1から2は20Ω、1から3は30Ω、2から4は16Ω、3から4は13Ωとなります。ここで頂点4から頂点1への接続はインピーダンス0[Ω]の理想電圧源のみです。ここは途中計算の都合上X[Ω]と置きます。
(* Conductance Matrix 1/x -> Inf *)
gb = IdentityMatrix[EdgeCount[g1]] {20, 30, 16, 13, x}^-1;
次に電圧源の行列を作ります。頂点4から1に電圧源V1[V]を定義します。
(* Voltage Source Matrix *)
v = {0,0,0,0,v1};
次に電流源の行列を作ります。回路図には電流源は無いので各ノードを0[A]とします。
(* Current Source Matrix *)
i = Table[0, {EdgeCount[g1]}];
次に回路図のグラフから辺結合行列(IncidenceMatrix)を作り、各ノードの電流と電圧を計算して、頂点4から頂点1の電圧÷電流から合成抵抗を求めます。電圧源はインピーダンス0[Ω]と考えるのでxは極限値の0[Ω]として計算します。
a = -1 Drop[1 IncidenceMatrix[g1], -1];
gn = a.gb.Transpose[a];
isn = (a.(gb.v - i));
vn = Inverse[gn].isn;
vb = Transpose[a].vn;
ib = -(gb.vb + i - gb.v);
Limit[vb, x -> 0][[5]]/Limit[ib, x -> 0][[5]] // N
Out[402]=19.5949
合成抵抗は約19.5949Ωと求まりました。
検算してみます。頂点1から頂点2経由で頂点4の合成抵抗は直列接続なので20+16=36Ω。
頂点1から頂点3経由で頂点4は30+13=43Ω。36Ωと43Ωの合成抵抗は並列接続なので(1/36+1/43)^-1≈19.5949Ωとなり合っています。
2 ブリッジ回路の合成抵抗
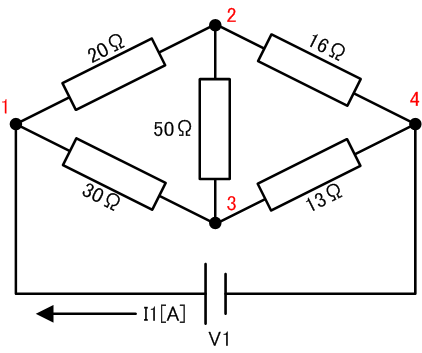
上図の様なブリッジ回路の合成抵抗を求めてみます。赤字は頂点を示します。
先と同様に回路の接続をグラフで表します。
Clear["Global`*"];
g1 = Graph[Range[4],
{1 -> 2, 1 -> 3, 2 -> 4, 3 -> 4, 2 -> 3, 4 -> 1}];
次にコンダクタンス(抵抗の逆数)の行列を作ります。回路図の頂点2から3への50Ωのブリッジ(橋)が追加になります。
(* Conductance Matrix 1/x -> Inf *)
gb = IdentityMatrix[EdgeCount[g1]] {20, 30, 16, 13, 50, x}^-1;
次に電圧源の行列を作ります。頂点4から1に電圧源V1[V]を定義します。橋の辺が追加されたので0が一つ増えます。
(* Voltage Source Matrix *)
v = {0,0,0,0,0,v1};
次に電流源の行列を作ります。回路図には電流源は無いので各ノードを0[A]とします。
(* Current Source Matrix *)
i = Table[0, {EdgeCount[g1]}];
次に先の回路と同様に計算します。ブリッジのノードが1個追加されたので、[[5]]ではなくて、6番目のノード[[6]]で合成抵抗を求めます。
a = -1 Drop[1 IncidenceMatrix[g1], -1];
gn = a.gb.Transpose[a];
isn = (a.(gb.v - i));
vn = Inverse[gn].isn;
vb = Transpose[a].vn;
ib = -(gb.vb + i - gb.v);
Limit[vb, x -> 0][[6]]/Limit[ib, x -> 0][[6]] // N
Out[509]=19.4815
合成抵抗は約19.4815Ωと求まりました。
検算してみます。△-Y変換を使います。頂点1で、20×30/(20+30+50)=6。頂点2で、20×50/(20+30+50)=10。頂点3で、30×50/(20+30+50)=15。直並列回路の合成抵抗を求めると、6+1/(1/(10+16) + 1/(15+13))≈19.4815Ωとなり、合っています。
3 Oh, so you think you're such a whiz at EE201?
ここからが本題です。TwitterでMatthew Skala氏(@mattskala)から、「ここのCircuit Diagramの右真ん中のウサギの巣(ラッツ・ネスト)の回路の合成抵抗を求めてみてください。」(意訳)とのツブヤキが私宛に来ました。Δ-Y変換で解けるのですが、なんか普通過ぎてツマラナイのでグラフと行列を使って合成抵抗を計算しました。
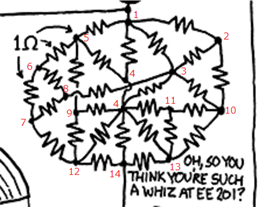
上図の回路は抵抗値が全て1Ω。頂点1から14の合成抵抗を求めます。
先の回路と同様に接続をグラフで表して、頂点1から14に電圧源があるとして、電流源はなしで、計算をします。
Clear["Global`*"];
g1 = Graph[Range[14],
{1 -> 2, 1 -> 3, 1 -> 4, 1 -> 5, 5 -> 6, 6 -> 7, 7 -> 8, 5 -> 9,
7 -> 12, 9 -> 12, 9 -> 4, 12 -> 14, 12 -> 4, 14 -> 13, 14 -> 4,
13 -> 11, 13 -> 4, 4 -> 11, 4 -> 3, 3 -> 2, 2 -> 10, 3 -> 10,
10 -> 13, 11 -> 10, 3 -> 8, 4 -> 5, 6 -> 8, 1 -> 14}];
(* Conductance Matrix 1/x -> Inf *)
gb = IdentityMatrix[
EdgeCount[g1]] Append[Table[1, {EdgeCount[g1] - 1}],
x]^-1;
(* Voltage Source Matrix *)
v = Append[Table[0, {EdgeCount[g1] - 1}], v1];
(* Current Source Matrix *)
i = Table[0, {EdgeCount[g1]}];
a = -1 Drop[1 IncidenceMatrix[g1], -1];
gn = a.gb.Transpose[a];
isn = (a.(gb.v - i));
vn = Inverse[gn].isn;
vb = Transpose[a].vn;
ib = -(gb.vb + i - gb.v);
Limit[vb, x -> 0][[28]]/Limit[ib, x -> 0][[28]]
Out[620]= 25265/33783
合成抵抗は33,783分の25,265と求まりました。約0.747861Ωになります。
検算はMatthew Skala氏が素晴らしいPrologのプログラムを書いて頂いたので、それを使います。
parallel_simplify(A,Z,M):-
delete(res(X,Y,R1),A,B),delete(res(X,Y,R2),B,C),
R3 is rational(1)/((rational(1)/R1)+(rational(1)/R2)),
sprintf(M,"Parallel: %w -- %w (%w||%w = %w)%n",[X,Y,R1,R2,R3]),
Z=[res(X,Y,R3)|C].
series_simplify(A,Z,M):-
delete(res(X,W,R1),A,B),delete(res(W,Y,R2),B,C),
W\=locked(_),
\+memberchk(res(_,W,_),C),\+memberchk(res(W,_,_),C),
R3 is R1+R2,
sprintf(M,"Series: %w -- %w -- %w (%w+%w = %w)%n",[X,W,Y,R1,R2,R3]),
Z=[res(X,Y,R3)|C].
series_simplify(A,Z,M):-
delete(res(W,X,R1),A,B),delete(res(W,Y,R2),B,C),X@<Y,
W\=locked(_),
\+memberchk(res(_,W,_),C),\+memberchk(res(W,_,_),C),
R3 is R1+R2,
sprintf(M,"Series: %w -- %w -- %w (%w+%w = %w)%n",[X,W,Y,R1,R2,R3]),
Z=[res(X,Y,R3)|C].
series_simplify(A,Z,M):-
delete(res(X,W,R1),A,B),delete(res(Y,W,R2),B,C),X@<Y,
W\=locked(_),
\+memberchk(res(_,W,_),C),\+memberchk(res(W,_,_),C),
R3 is R1+R2,
sprintf(M,"Series: %w -- %w -- %w (%w+%w = %w)%n",[X,W,Y,R1,R2,R3]),
Z=[res(X,Y,R3)|C].
wye_delta_simplify(A,Z,M):-
(delete(res(N1,NX,R1),A,B);delete(res(NX,N1,R1),A,B)),
(delete(res(N2,NX,R2),B,C);delete(res(NX,N2,R2),B,C)),N1@<N2,
(delete(res(N3,NX,R3),C,D);delete(res(NX,N3,R3),C,D)),N2@<N3,
NX\=locked(_),
\+memberchk(res(_,NX,_),D),\+memberchk(res(NX,_,_),D),
RNum is (R1*R2)+(R2*R3)+(R1*R3),
RA is rational(RNum)/R1,
RB is rational(RNum)/R2,
RC is rational(RNum)/R3,
sprintf(M,"Wye -> delta, remove %w%n",[NX]),
Z=[res(N1,N2,RC),res(N2,N3,RA),res(N1,N3,RB)|D].
spare_node_name(foo).
spare_node_name(bar).
spare_node_name(baz).
spare_node_name(quux).
spare_node_name(alice).
spare_node_name(bob).
spare_node_name(carol).
spare_node_name(dave).
delta_wye_simplify(A,Z,M):-
delete(res(N1,N2,RC),A,B),
delete(res(N2,N3,RA),B,C),
delete(res(N1,N3,RB),C,D),
spare_node_name(NX),
\+memberchk(res(_,NX,_),D),\+memberchk(res(NX,_,_),D),
RDenom is RA+RB+RC,
R1 is rational(RB*RC)/RDenom,
R2 is rational(RA*RC)/RDenom,
R3 is rational(RA*RB)/RDenom,
(N1@<NX->RI1=res(N1,NX,R1);
RI1=res(NX,N1,R1)),
(N2@<NX->RI2=res(N2,NX,R2);
RI2=res(NX,N2,R2)),
(N3@<NX->RI3=res(N3,NX,R3);
RI3=res(NX,N3,R3)),
sprintf(M,"Delta -> wye, insert %w among %w, %w, %w%n",[NX,N1,N2,N3]),
Z=[RI1,RI2,RI3|D].
all_simplify(A,Z):-
series_simplify(A,X,M),!,
write(M),
all_simplify(X,Z).
all_simplify(A,Z):-
parallel_simplify(A,X,M),!,
write(M),
all_simplify(X,Z).
all_simplify(A,Z):-
wye_delta_simplify(A,X,M),!,
write(M),
all_simplify(X,Z).
all_simplify(A,Z):-
delta_wye_simplify(A,X,M1),
series_simplify(X,Y,M2),!,
write(M1),write(M2),
all_simplify(Y,Z).
all_simplify(A,Z):-
delta_wye_simplify(A,X,M1),
parallel_simplify(X,Y,M2),!,
write(M1),write(M2),
all_simplify(Y,Z).
all_simplify(A,Z):-
delta_wye_simplify(A,X,M1),
delta_wye_simplify(X,Y,M2),
series_simplify(Y,W,M3),!,
write(M1),write(M2),write(M3),
all_simplify(W,Z).
all_simplify(A,A).
xkcd_problem([
res(a,locked(x),1),res(b,locked(x),1),res(c,locked(x),1),res(d,locked(x),1),
res(a,b,1),res(a,e,1),res(a,h,1),
res(b,c,1),res(b,h,1),res(b,i,1),res(b,k,1),res(b,l,1),res(b,locked(y),1),
res(c,d,1),res(c,f,1),res(c,j,1),
res(d,j,1),
res(e,f,1),res(e,g,1),
res(f,g,1),
res(g,l,1),
res(h,l,1),
res(i,k,1),res(i,j,1),
res(j,k,1),
res(k,locked(y),1),
res(l,locked(y),1)
]).
ECLiPSeを起動して、下記の要領でQueryを発行すると、
[eclipse 1]: [deltawye].
[eclipse 2]: xkcd_problem(X),all_simplify(X,Y).
途中結果省略
Parallel: bar -- locked(x) (71273861175_58183029877||863925590_871760449 = 18150_33131)
Parallel: bar -- locked(y) (27225_10577||3_7 = 27225_74102)
Series: locked(x) -- bar -- locked(y) (18150_33131+27225_74102 = 45855975_50103538)
Parallel: locked(x) -- locked(y) (45855975_50103538||9075_2219 = 25265_33783)
X = [res(a, locked(x), 1), res(b, locked(x), 1), res(c, locked(x), 1), res(d, locked(x), 1), res(a, b, 1), res(a, e, 1), res(a, h, 1), res(b, c, 1), res(b, h, 1), res(b, i, 1), res(b, k, 1), res(b, l, 1), res(b, locked(y), 1), res(c, d, 1), res(c, f, 1), res(c, j, 1), res(d, j, 1), res(e, f, 1), res(...), ...]
Y = [res(locked(x), locked(y), 25265_33783)]
Yes (0.07s cpu)
25265_33783と答えが帰ってきます。