\newcommand{\quadform}[2]{\left\lVert#1\right\rVert_{#2}^{2}}
\newcommand{\Const}{\mathrm{Const.}}
\newcommand{\T}{\mathsf{T}}
\newcommand{\pdr}[2]{\frac{\partial #1}{\partial #2}}
\newcommand{\argmin}{\mathop{\mathrm{argmin}}\limits}
1. はじめに
目標値や外乱などの外生信号が印加される制御系において、これらの未来の値を用いて制御を行う「予見制御」について解説したいと思います。
2. 問題設定
今回は外乱抑制を題材に、入力端外乱が印加される可制御な離散時間制御対象
x_{k+1}=Ax_{k}+Bu_{k}+d_{k}
に対し、親の顔より見た二次形式評価関数
\sum_{k=0}^{\infty}\left(\quadform{x_k}{Q}+\quadform{u_k}{R}\right)\\
\quadform{x}{Q}:=x^{\T}Qx,\quadform{u}{R}:=u^{\T}Ru\\
Q\succeq0, R\succ0
を最小化する制御則を考えます。
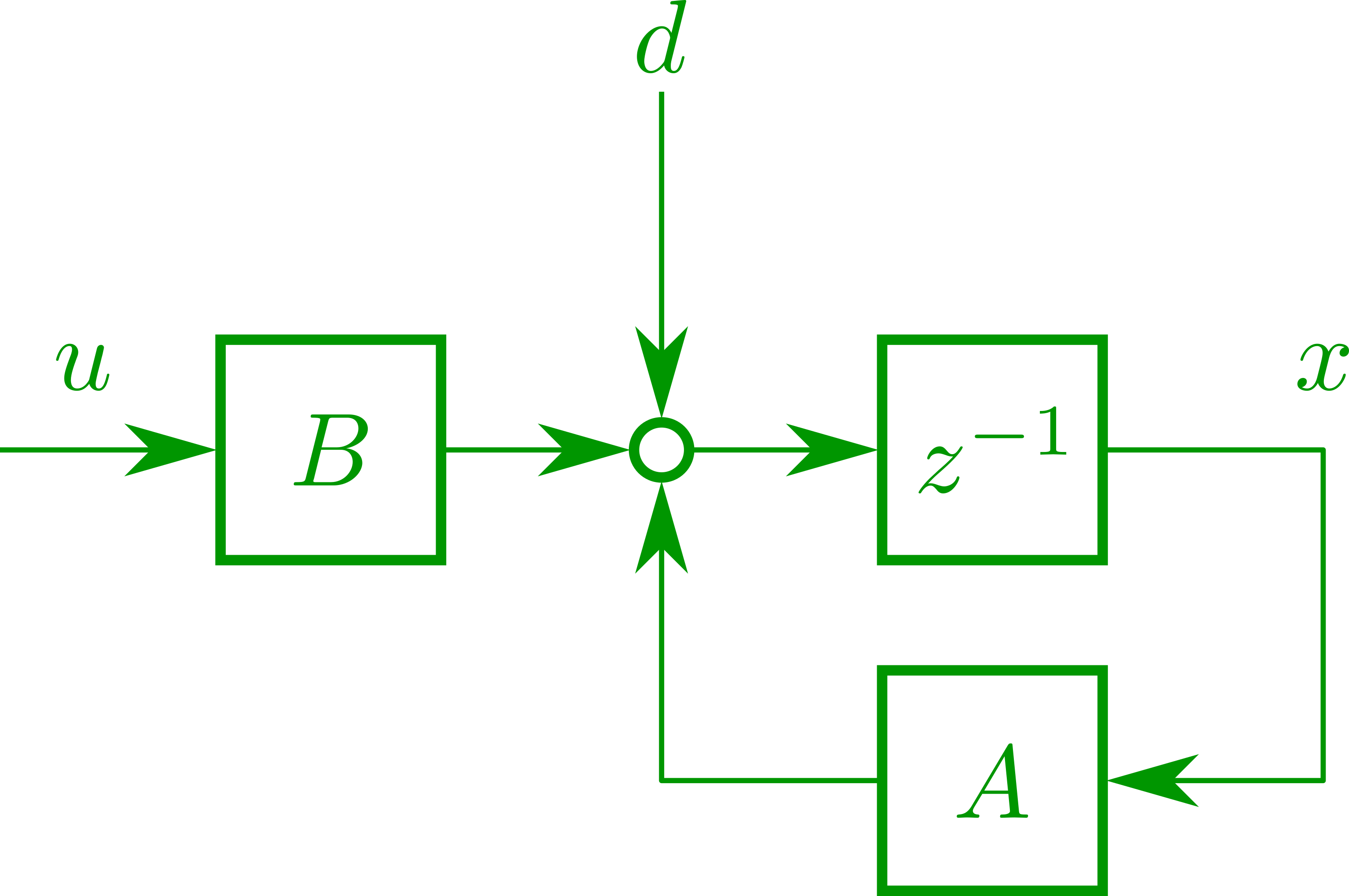
外乱予見を行わない場合、つまり$d\equiv0$を仮定して設計を行うときは通常のLQR問題であり、最適制御入力は離散時間代数Riccati方程式
P=A^{\T}PA-A^{\T}PB\left(B^{\T}PB+R\right)^{-1}B^{\T}PA+Q
の解$P$を用いた状態フィードバック
\begin{aligned}
u_{k}&=-Fx_{k}\\
F&:=\left(B^{\T}PB+R\right)^{-1}B^{\T}PA
\end{aligned}
にて表されます。
3. 予見制御
では外乱の予見が可能な場合はどうでしょうか?以下では動的計画法にて外乱予見付きの最適制御を導出します。
3.1 評価関数の再定義
まずは前述の評価関数の区間を$[0,K]$とし、
\sum_{k=0}^{K}\left(\quadform{x_k}{Q}+\quadform{u_k}{R}\right)
とおきます。この評価関数において、初期状態$x_0$は制御入力により操作できない定数項です。また、最終入力$u_K$は評価区間のどの状態にも影響を与えないため、$u_K=0$が自明な最適値となります。したがって、これらの2項を排除した等価な評価関数
J:=\sum_{k=0}^{K-1}\left(\quadform{x_{k+1}}{Q}+\quadform{u_k}{R}\right)
を考えることができます。
3.2 有限時間最適制御の導出
評価関数$J$を最適化して最適制御則を導きます。ここで、評価関数の区間$k\in[k_1,k_2]$における評価値を
J_{[k_1,k_2]}=\sum_{k=k_1}^{k_2}\left(\quadform{x_{k+1}}{Q}+\quadform{u_k}{R}\right)
で表します。$J=J_{[0,K-1]}$であるため、以下では$J_{[K-1,K-1]},J_{[K-2,K-1]},J_{[K-3,K-1]},\ldots,J_{[0,K-1]}$と順次最適化を行うことを考えます。
まず、最終ステップ$k=K-1$における評価関数値
J_{[K-1,K-1]}=\quadform{x_{K}}{Q}+\quadform{u_{K-1}}{R}
を考え、$u_{K-1}$が$J_{[K-1,K-1]}$にのみ影響することから、最終ステップの最適制御入力
u_{K-1}^{*}=\argmin_{u_{K-1}}J_{[K-1,K-1]}
を求めます。ここで、天下り的ですが$x$に関する二次項と一次項の係数
P_K:=Q, \eta_K:=0
を導入し、評価関数を
J_{[K-1,K-1]}=\quadform{x_{K}}{P_K}+2x_{K}^{\T}\eta_{K}+\quadform{u_{K-1}}{R}
と書き換えます。$x_{K}=Ax_{K-1}+Bu_{K-1}+d_{K-1}$を代入し、
\begin{aligned}
J_{[K-1,K-1]}&=\quadform{x_{K}}{P_K}+2x_{K}^{\T}\eta_{K}+\quadform{u_{K-1}}{R}\\
&=\quadform{x_{K-1}}{A^{\T}P_{K}A}+2x_{K-1}^{\T}A^{\T}\left(P_{K}d_{K-1}+\eta_{K}\right)\\
&\quad +2u_{K-1}^{\T}B^{\T}\left(P_{K}Ax_{K-1}+P_{K}d_{K-1}+\eta_{K}\right)\\
&\quad +\quadform{u_{K-1}}{B^{\T}P_{K}B+R}+\Const\\
\end{aligned}
を得ます。上式は$u_{K-1}$に対して二次であり、かつ定義より$B^{\T}P_{K}B+R\succ0$であるため、最適制御入力$u_{K-1}^{*}$は一次最適性条件
\pdr{J_{[K-1,K-1]}}{u_{K-1}}\left(u_{K-1}^{*}\right)=2B^{\T}\left(P_{K}Ax_{K-1}+P_{K}d_{K-1}+\eta_{K}\right)+2\left(B^{\T}P_{K}B+R\right)u_{K-1}^{*}=0
を満たす唯一の解です。これを解き、最終ステップの最適制御則
\begin{aligned}
u_{K-1}^{*}&=-\left(B^{\T}P_{K}B+R\right)^{-1}B^{\T}\left(P_{K}Ax_{K-1}+P_{K}d_{K-1}+\eta_{K}\right)\\
&=-F_{K-1}x_{k-1}+g_{K-1}\\
F_{K-1}&:=\left(B^{\T}P_{K}B+R\right)^{-1}B^{\T}P_{K}A\\
g_{K-1}&:=-\left(B^{\T}P_{K}B+R\right)^{-1}B^{\T}\left(P_{K}d_{K-1}+\eta_{K}\right)
\end{aligned}
が得られます。ここに、$F_{K-1}$は$k=K-1$における状態フィードバックゲイン、$g_{K-1}$は外乱$d$のフィードフォワード入力です。この制御則のもと、$J_{[K-1,K-1]}$の最適値は
\begin{aligned}
J_{[K-1,K-1]}^{*}&=J_{K-1}(u_{K-1}^{*})\\
&=\quadform{x_{K-1}}{A^{\T}P_{K}A}+2x_{K-1}^{\T}A^{\T}\left(P_{K}d_{K-1}+\eta_{K}\right)\\
&\quad -\quadform{-F_{K-1}x_{k-1}+g_{K-1}}{B^{\T}P_{K}B+R}+\Const\\
&=\quadform{x_{K-1}}{A^{\T}P_{K}A-F_{K-1}^{\T}\left(B^{\T}P_{K}B+R\right)F_{K-1}}\\
&\quad +2x_{K-1}^{\T}\left(A^{\T}\left(P_{K}d_{K-1}+\eta_{K}\right)+F_{K-1}^{\T}\left(B^{\T}P_{K}B+R\right)g_{K-1}\right)+\Const
\end{aligned}
となります。
つづいて、$u_{k-1}=u_{K-1}^{*}$を前提に$J_{[K-2,K-1]}$を最適化します。
\begin{aligned}
\left.J_{[K-2,K-1]}\right\rvert_{u_{K-1}=u_{K-1}^{*}}&=\quadform{x_{K-1}}{Q}+\quadform{u_{K-2}}{R}+J_{[K-1,K-1]}^{*}\\
&=\quadform{x_{K-1}}{Q}+\quadform{u_{K-2}}{R}+\quadform{x_{K-1}}{A^{\T}P_{K}A-F_{K-1}^{\T}\left(B^{\T}P_{K}B+R\right)F_{K-1}}\\
&\quad +2x_{K-1}^{\T}\left(A^{\T}\left(P_{K}d_{K-1}+\eta_{K}\right)+F_{K-1}^{\T}\left(B^{\T}P_{K}B+R\right)g_{K-1}\right)+\Const\\
&=\quadform{x_{K-1}}{A^{\T}P_{K}A-F_{K-1}^{\T}\left(B^{\T}P_{K}B+R\right)F_{K-1}+Q}+\quadform{u_{K-2}}{R}\\
&\quad +2x_{K-1}^{\T}\left(A^{\T}\left(P_{K}d_{K-1}+\eta_{K}\right)+F_{K-1}^{\T}\left(B^{\T}P_{K}B+R\right)g_{K-1}\right)+\Const
\end{aligned}
再び$x$の二次項、一次項の係数を
\begin{aligned}
P_{K-1}&=A^{\T}P_{K}A-F_{K-1}^{\T}\left(B^{\T}P_{K}B+R\right)F_{K-1}+Q\\
\eta_{K-1}&=A^{\T}\left(P_{K}d_{K-1}+\eta_{K}\right)+F_{K-1}^{\T}\left(B^{\T}P_{K}B+R\right)g_{K-1}
\end{aligned}
とおくと、
\left.J_{[K-2,K-1]}\right\rvert_{u_{K-1}=u_{K-1}^{*}}=\quadform{x_{K-1}}{P_{K-1}}+2x_{K-1}^{\T}\eta_{k-1}+\quadform{u_{K-2}}{R}+\Const
となり$J_{[K-1,K-1]}$と同じ構造に帰着されます。したがって、以降の計算はすべて漸化式
\begin{aligned}
P_{k-1}&=A^{\T}P_{k}A-F_{k-1}^{\T}\left(B^{\T}P_{k}B+R\right)F_{k-1}+Q\\
\eta_{k-1}&=A^{\T}\left(P_{k}d_{k-1}+\eta_{k}\right)+F_{k-1}^{\T}\left(B^{\T}P_{k}B+R\right)g_{k-1}\\
F_{k-1}&=\left(B^{\T}P_{k}B+R\right)^{-1}B^{\T}P_{k}A\\
g_{k-1}&=-\left(B^{\T}P_{k}B+R\right)^{-1}B^{\T}\left(P_{k}d_{k-1}+\eta_{k}\right)
\end{aligned}
を境界条件$P_{K}=Q,\eta_{K}=0$について解くことで代えることができ、各ステップでの最適制御入力が
u_{k}^{*}=-F_{k}x_{k}+g_{k}
として得られます。
3.3 定常解の導出
$P$に関する漸化式に$F_{k-1}=\left(B^{\T}P_{k}B+R\right)^{-1}B^{\T}P_{k}A$を代入すると、離散時間動的Riccati方程式
P_{k-1}=A^{\T}P_{k}A-A^{\T}P_{k}B\left(B^{\T}P_{k}B+R\right)B^{\T}P_{k}A+Q
が得られます。ここでは$K$が十分大きいとの仮定のもと、$P_k$を代数Riccati方程式の解$P$で置換することを考えます。このとき、他の漸化式は
\begin{aligned}
F&=\left(B^{\T}PB+R\right)^{-1}B^{\T}PA\\
g_{k-1}&=-\left(B^{\T}PB+R\right)^{-1}B^{\T}\left(Pd_{k-1}+\eta_{k}\right)\\
\eta_{k-1}&=A^{\T}\left(Pd_{k-1}+\eta_{k}\right)+F^{\T}\left(B^{\T}PB+R\right)g_{k-1}\\
&=\left(A-BF\right)^{\T}\left(Pd_{k-1}+\eta_{k}\right)\\
\end{aligned}
となります。$F$はLQR問題を解いて得られる最適状態フィードバックゲインに等しく、予見ありの最適制御則はLQRと外乱フィードフォワードを併せた
u_k^{*}=-Fx_k+g_k
として表すことができます。
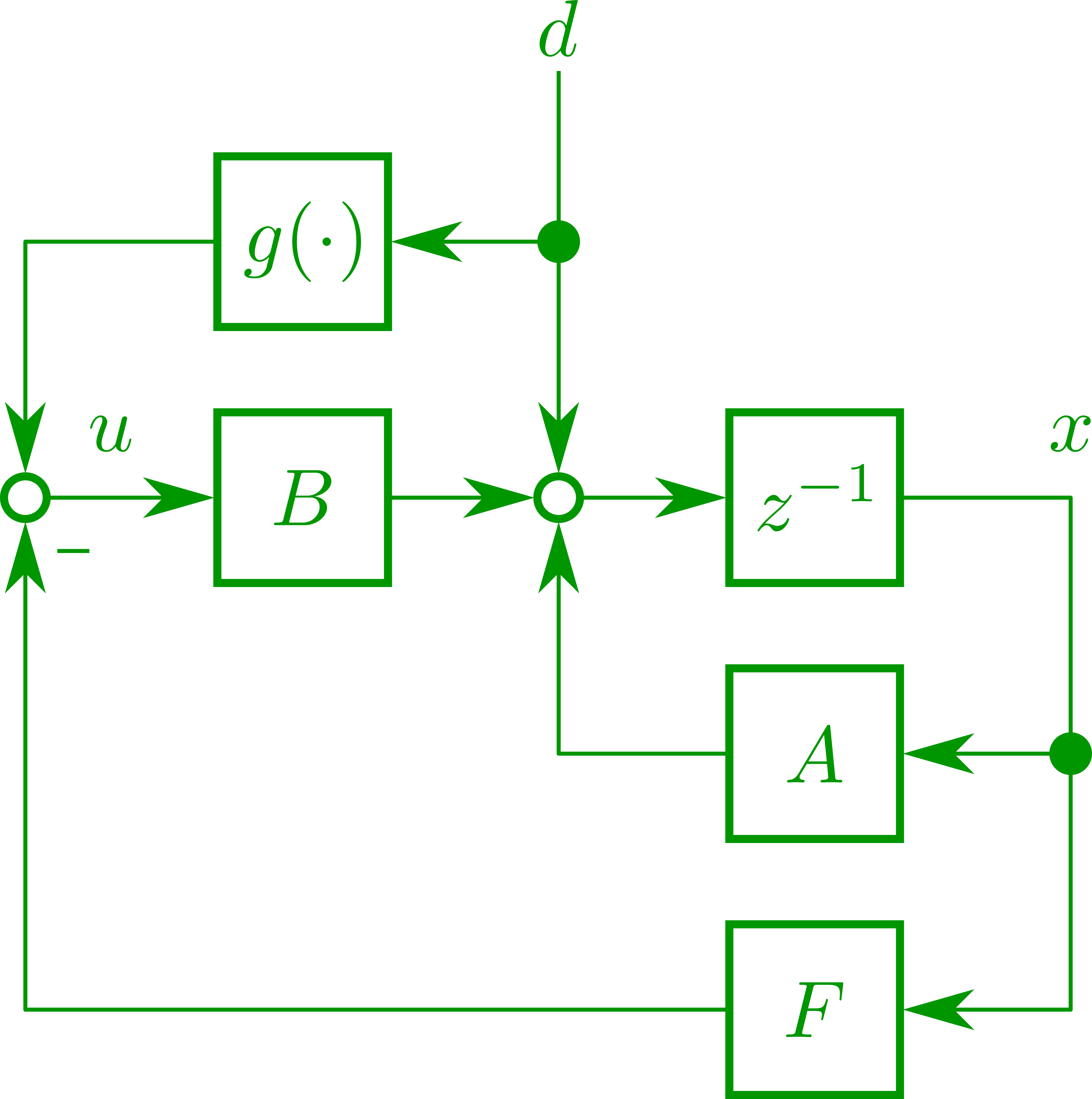
さらに、フィードフォワード入力$g_{k}$に関してはいま少し見通しの良いかたちに変形できるため計算を進めます。まず$\eta_k$に注目し、$\Phi:=\left(A-BF\right)^{\T}$とおくと、
\eta_{k-1}=\Phi\eta_{k}+\Phi Pd_{k-1}
なる(ステップ減少方向の)状態方程式であることがわかります。境界条件$\eta_K=0$に注意してこれを解くと、
\begin{aligned}
\eta_{K-k'}&=\sum_{l=0}^{k'-1}\Phi^{k'-1-l}\Phi Pd_{K-1-l}\\
&=\sum_{l=0}^{k'-1}\Phi^{k'-l}Pd_{K-1-l}
\end{aligned}
です。$g_k$の計算に必要な$\eta_{k+1}$を求めると、
\begin{aligned}
\eta_{k+1}&=\sum_{l=0}^{k'-1}\Phi^{k'-1-l}\Phi Pd_{K-1-l}\\
&=\sum_{l=0}^{K-k-2}\Phi^{K-k-1-l}Pd_{K-1-l}\\
&=\sum_{l=1}^{K-k-1}\Phi^{l}Pd_{k+l}\\
\end{aligned}
となります。これをもとに$g_k$は
\begin{aligned}
g_{k}&=-\left(B^{\T}PB+R\right)^{-1}B^{\T}\left(Pd_{k}+\eta_{k+1}\right)\\
&=-\left(B^{\T}PB+R\right)^{-1}B^{\T}\left(Pd_{0}+\sum_{l=1}^{K-k-1}\Phi^{l}Pd_{k+l}\right)\\
&=-\left(B^{\T}PB+R\right)^{-1}B^{\T}\sum_{l=0}^{K-k-1}\Phi^{l}Pd_{k+l}
\end{aligned}
と得られ、現在時刻以降の外乱の値にゲインを乗じて総和したものがフィードフォワード入力として利用されます。ここでべき乗されている$\Phi=\left(A-BF\right)^{\T}$はLQRの閉ループ系のシステム行列(の転置)なのでSchur安定であり、未来の外乱の影響は次第に減少することになります。このため、予見ステップ数を適当に打ち切り、たとえば現在から$L$ステップ間の予見を行うよう実装します。
g_{k}=-\left(B^{\T}PB+R\right)^{-1}B^{\T}\sum_{l=0}^{L-1}\Phi^{l}Pd_{k+l}
4. 設計例
Julia 1.7.0を用いたシミュレーションにより、予見制御の有無による挙動の違いを検証します。制御対象と最適化の重みは以下の通りです。
\begin{aligned}
A &= \begin{bmatrix}0.9044&-0.0304\\0.0297&0.9995\end{bmatrix}\\
B &= \begin{bmatrix}1\\1\end{bmatrix}\\
Q &= \begin{bmatrix}1&0\\0&1\end{bmatrix}\\
R &= 1
\end{aligned}
また、外乱の予見ステップ数は$L=100$とします。外乱$d$は2次元目に100ステップ目から一周期の正弦波を印加します。
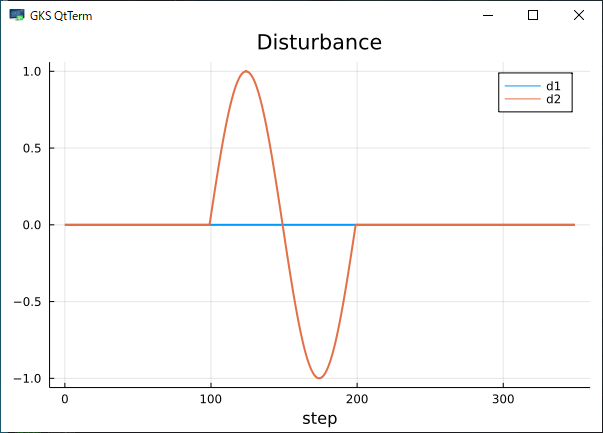
上記の条件のもと、以下のJuliaコードを作成しました。
# 必要モジュールのロード
using ControlSystems
using Plots
using LinearAlgebra
using Printf
# プラントパラメータ
A = [0.9044 -0.0304; 0.0297 0.9995];
B = [1; 1];
# 最適化重み
Q = Matrix{Float64}(1I, size(A));
R = Matrix{Float64}(1I, size(B, 2), size(B, 2));
# 離散時間代数Riccati方程式の解
P = dare(A, B, Q, R);
# 最適フィードバックゲイン
F = (transpose(B)*P*B.+R) \ transpose(B)*P*A
# シミュレーションステップ数
K = 350;
# 予見ステップ数
L = 100;
# 状態・入力ベクトル(LQR用)
x_lqr = zeros(Float64, size(A,1), K);
u_lqr = zeros(Float64, size(B,2), K);
# 状態・入力ベクトル(LQR+予見制御用)
x_prv = zeros(Float64, size(A,1), K);
u_prv = zeros(Float64, size(B,2), K);
# 外乱
d = zeros(Float64, size(A,1), K+L);
d[2, 100:200] .= sin.(2*pi*(0:100)/100);
# 外乱フィードフォワードゲイン
Phi = transpose(A-B*F);
G = zeros(Float64, size(B,2), L*size(A,1));
Gl = (transpose(B)*P*B.+R) \ transpose(B);
for l = 1:L
global Gl;
G[:,1+size(A,2)*(l-1):size(A,2)*l] = Gl*P;
Gl = Gl*Phi;
end
# シミュレーションループ
for k = 1:K-1
u_lqr[:,k] = - F*x_lqr[:,k];
x_lqr[:,k+1] = A*x_lqr[:,k] + B*u_lqr[k] + d[:,k];
u_prv[:,k] = - F*x_prv[:,k] - G*(d[:,k.+(0:L-1)][:]);
x_prv[:,k+1] = A*x_prv[:,k] + B*u_prv[k] + d[:,k];
end
# LQR/LQR+予見制御の評価関数値
J_lqr = sum(x_lqr .* (Q*x_lqr)) + sum(u_lqr .* (R*u_lqr))
J_prv = sum(x_prv .* (Q*x_prv)) + sum(u_prv .* (R*u_prv))
@printf("J(LQR) = %f\n", J_lqr)
@printf("J(LQR+Preview) = %f\n", J_prv)
# プロット
k = 0:K-1
px1 = plot(k, [x_lqr[1,:], x_prv[1,:]], label=["LQR" "LQR+Preview"], ylabel="x1", lw=2)
px2 = plot(k, [x_lqr[2,:], x_prv[2,:]], label=["LQR" "LQR+Preview"], ylabel="x2", lw=2)
pu = plot(k, [u_lqr', u_prv'], label=["LQR" "LQR+Preview"], ylabel="u", xlabel="step", lw=2)
plot(px1, px2, pu, layout=(3,1), reuse = false)
結果の時系列は以下の通りになりました。予見制御の導入により、外乱が印加される100ステップ目以前から入力が行われ、外乱に対して「身構えている」ことがわかります。
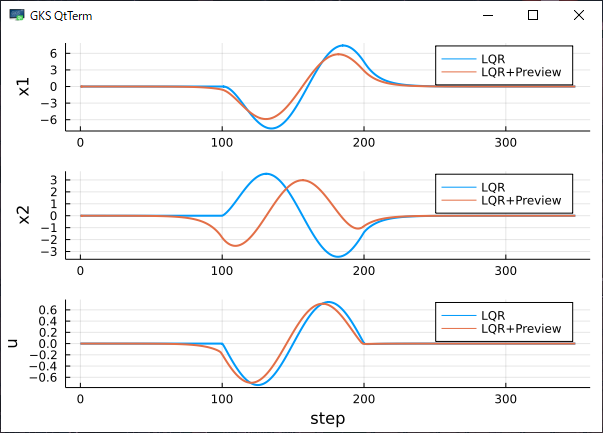
具体的な性能の変化は評価関数ベースで
- LQR: $J=3593.558878$
- LQR+予見制御: $J=2237.295404$
となり、改善が確認できます。