車輪型移動ロボットのMPCでの軌道追従制御

$\def\bm{\boldsymbol}$

ルンバのような車輪型移動ロボットの一つである対向2輪型移動ロボットについて、モデル予測制御（MPC）を使った軌道追従制御をPythonで行ってみたので、紹介します。

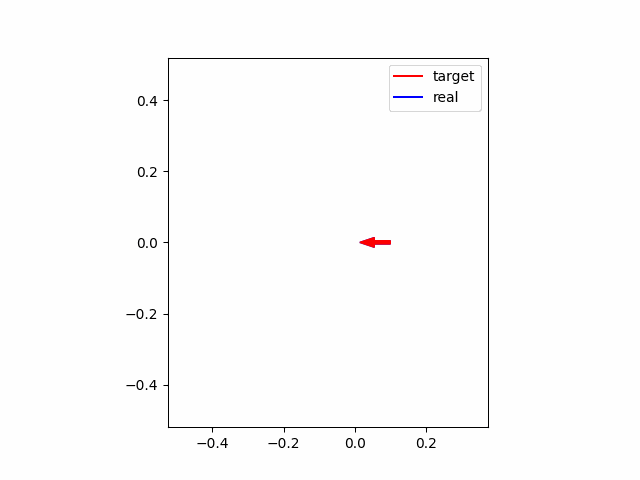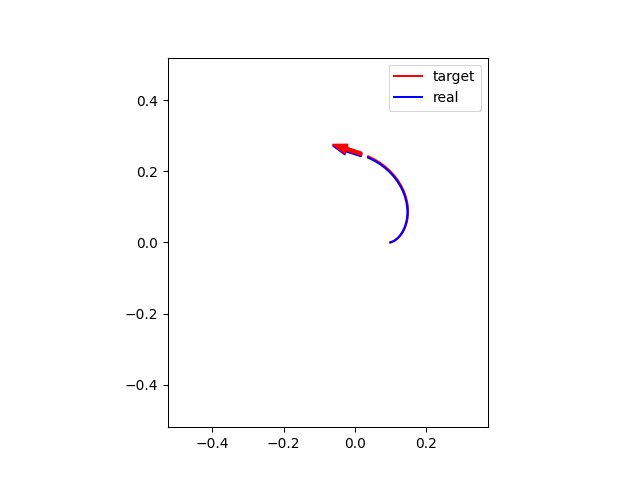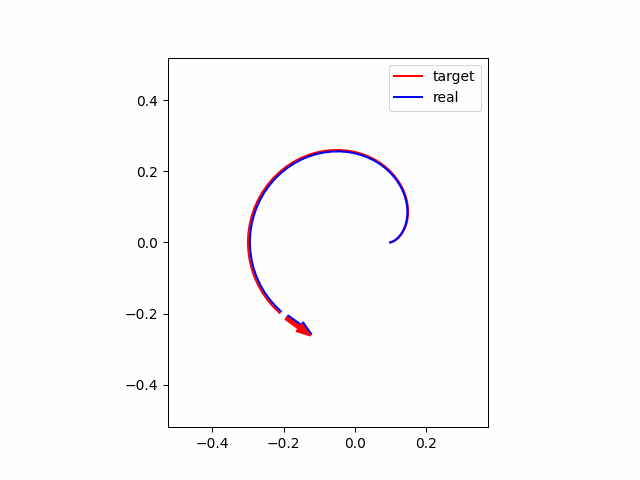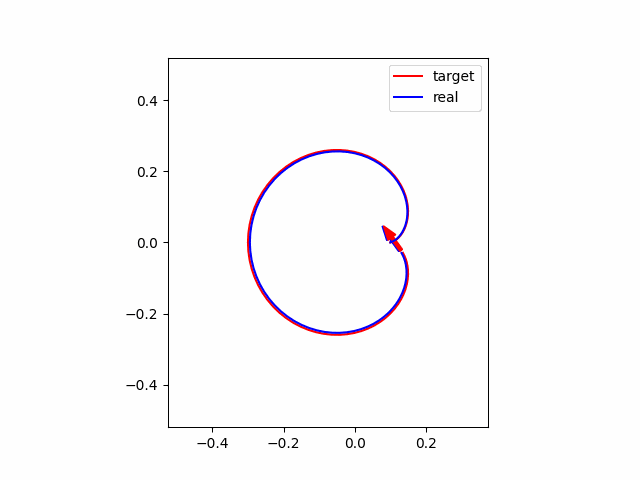
結論として、MPCを動かしてみた結果は以下のようになります。赤線・赤矢印がそれぞれ追従すべき軌跡・方向を表し、青線・青矢印が実際のロボットの軌跡・方向を表します。グラフを見ると、かなり追従できている様子が伺えます。

また、githubに以下で説明したプログラムを共有します。

MPCの勉強には、以下のサイトを参考にしました。

• モデル予測制御（MPC）による軌道追従制御

対向2輪型移動ロボットの状態方程式の導出

対向2輪型移動ロボットの状態方程式を考えていくために、以下の図のようにロボットの形状をパラメータ$l,\alpha$で指定することにします。以降では$l$を車輪間距離、$\alpha$を車輪配置角度と呼ぶことにします。

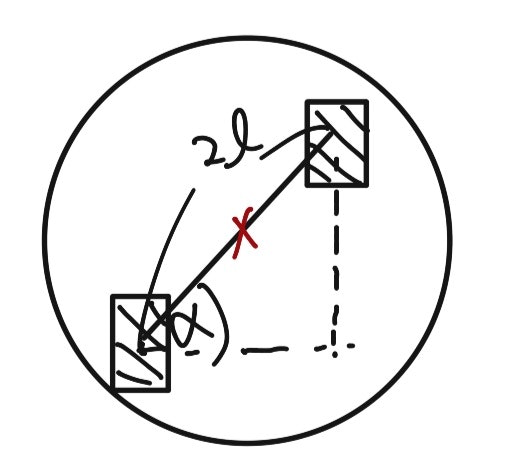
ロボットの状態方程式を求めるために、任意の剛体運動は並進$v_{\parallel}$と回転$v_{\perp}$に分解できることを用います。右・左タイヤの速度をそれぞれ$v_R, v_L$とおいて、

v_{\parallel} = \frac{v_R + v_L}{2}, v_{\perp} = \frac{v_R - v_L}{2}

と置くことにすると、下の図のように運動を並進と回転に分解できます。

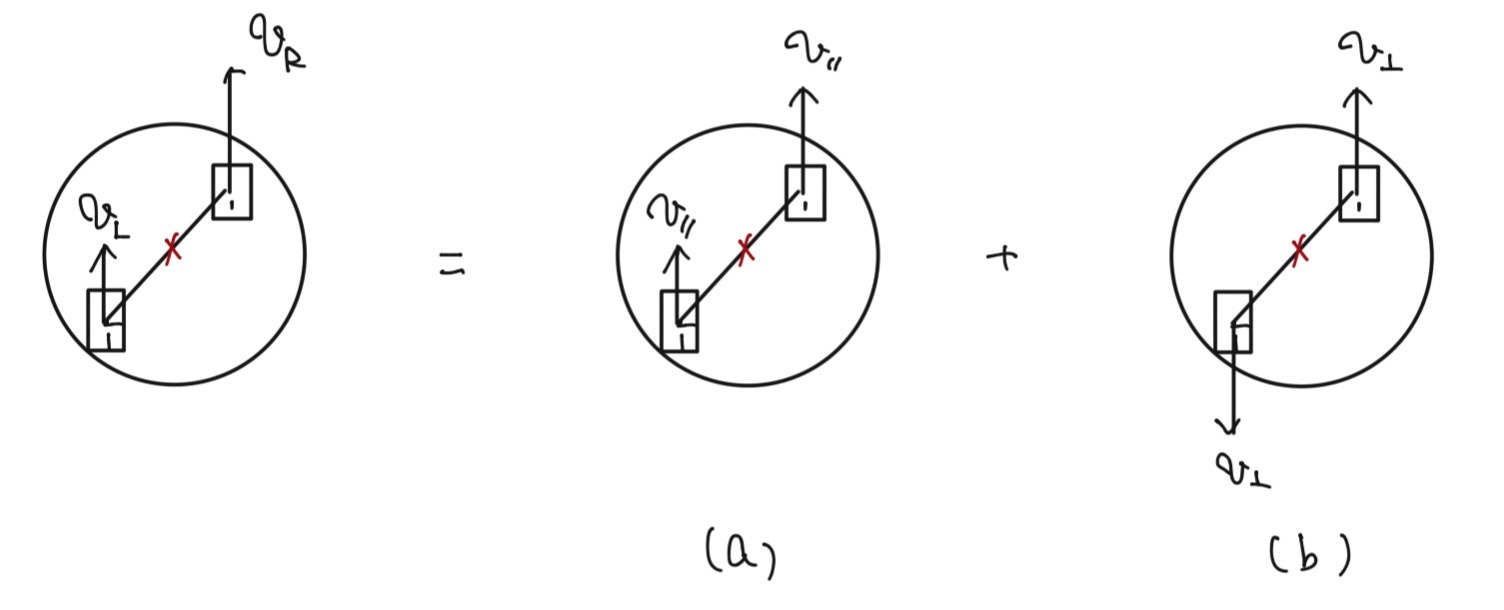
上の分解によって、

• 図(a)の動きに関しては、明らかに$v_{\parallel}=(v_R + v_L)/2$でタイヤと並行に動く
• 図(b)の動きに関しては、角速度$\omega=v_{\perp}\cos \alpha /l = (v_R - v_L) \cos \alpha /(2l)$で回転する（下図参照。タイヤは滑らないと仮定）
  

となります。以上を統合すると、タイヤを速度$v_R,v_L$で回転させると、

• タイヤと並行に$v=(v_R + v_L)/2$で移動
  しつつ
• 角速度$ \omega=(v_R - v_L)/2 \times \cos \alpha /l$で中心周りに回転

することがわかります。
以上を踏まえると、対向2輪型差動移動ロボットの状態方程式は、

\begin{aligned}
\dot{x} &= v \cos \theta \\
\dot{y} &= v \sin \theta \\
\dot{\theta} &= \omega
\end{aligned}

となります。
ただし、

\begin{aligned}
v &= \frac{v_R + v_L}{2} \\
\omega &= \frac{v_R - v_L}{2l} \cos \alpha 
\end{aligned}

です。
上の状態方程式をもとに、ロボットの動作をシミュレーションするコードは以下になります。ここで、上の状態方程式の時間発展を計算するのには4次のルンゲクッタ法を用いました。

class DiffCar:
	"""差動駆動車のクラス"""
	def __init__(self,wheel_distance:float,wheel_angle:float,x_init:float=0,y_init:float=0,theta_init:float=0):
		"""
		差動駆動車の初期化

		Parameters
		----------
		wheel_distance : float
			 車輪間距離
		wheel_angle : float
			 車輪配置角度
		x_init : float, optional
			 車の初期x座標, by default 0
		y_init : float, optional
			 車の初期y座標, by default 0
		theta_init : float, optional
			 車の初期姿勢, by default 0
		"""
		self.wheel_distance = wheel_distance
		self.wheel_angle = wheel_angle
		self.x = x_init
		self.y = y_init
		self.theta = theta_init
  
	def x_dot(self,x,y,theta,v_R,v_L):
		v = (v_R + v_L)/2
		x_dot = v*np.cos(theta)
		return x_dot

	def y_dot(self,x,y,theta,v_R,v_L):
		v = (v_R + v_L)/2
		y_dot = v*np.sin(theta)
		return y_dot

	def theta_dot(self,x,y,theta,v_R,v_L):
		v = (v_R + v_L)/2
		omega = (v_R - v_L)/(2*self.wheel_distance) *np.cos(self.wheel_angle)
		theta_dot = omega
		return theta_dot

	def dynamics(self,v_R:float,v_L:float) -> Tuple[float, float, float]:
		"""
		車輪の速度をv_R,v_Lとしたときの運動方程式を返す

		Parameters
		----------
		v_R : float
			 右車輪の速度
		v_L : float
			 左車輪の速度

		Returns
		-------
		Tuple[float, float, float]
			車の速度と角速度 
		"""
  
		v = (v_R + v_L)/2
		omega = (v_R - v_L)/self.wheel_distance *np.cos(self.wheel_angle)
		x_dot = v*np.cos(self.theta)
		y_dot = v*np.sin(self.theta)
		theta_dot = omega
		return x_dot,y_dot,theta_dot

	def runge_kutta_step(self,x, y, theta, dt, v_R, v_L):
		k1_x = dt * self.x_dot(x, y, theta, v_R, v_L)
		k1_y = dt * self.y_dot(x, y, theta, v_R, v_L)
		k1_theta = dt * self.theta_dot(x, y, theta, v_R, v_L)

		k2_x = dt * self.x_dot(x + 0.5 * k1_x, y + 0.5 * k1_y, theta + 0.5 * k1_theta, v_R, v_L)
		k2_y = dt * self.y_dot(x + 0.5 * k1_x, y + 0.5 * k1_y, theta + 0.5 * k1_theta, v_R, v_L)
		k2_theta = dt * self.theta_dot(x + 0.5 * k1_x, y + 0.5 * k1_y, theta + 0.5 * k1_theta, v_R, v_L)

		k3_x = dt * self.x_dot(x + 0.5 * k2_x, y + 0.5 * k2_y, theta + 0.5 * k2_theta, v_R, v_L)
		k3_y = dt * self.y_dot(x + 0.5 * k2_x, y + 0.5 * k2_y, theta + 0.5 * k2_theta, v_R, v_L)
		k3_theta = dt * self.theta_dot(x + 0.5 * k2_x, y + 0.5 * k2_y, theta + 0.5 * k2_theta, v_R, v_L)

		k4_x = dt * self.x_dot(x + k3_x, y + k3_y, theta + k3_theta, v_R, v_L)
		k4_y = dt * self.y_dot(x + k3_x, y + k3_y, theta + k3_theta, v_R, v_L)
		k4_theta = dt * self.theta_dot(x + k3_x, y + k3_y, theta + k3_theta, v_R, v_L)

		x_next = x + (k1_x + 2*k2_x + 2*k3_x + k4_x) / 6.0
		y_next = y + (k1_y + 2*k2_y + 2*k3_y + k4_y) / 6.0
		theta_next = theta + (k1_theta + 2*k2_theta + 2*k3_theta + k4_theta) / 6.0

		return x_next, y_next, theta_next

	def step(self,v_R:float,v_L:float,dt:float):
		"""
		車輪の速度をv_R,v_Lとして、dt時間だけ車を動かして、位置と姿勢を更新する

		Parameters
		----------
		v_R : float
				右車輪の速度
		v_L : float
				左車輪の速度
		dt : float
				時間
    
		Returns
		-------
		Tuple[float, float, float]
			車の位置と角度 
		"""
		#４次ルンゲクッタ法を用いて、位置と姿勢を更新
		self.x, self.y,self.theta = self.runge_kutta_step(self.x, self.y, self.theta, dt, v_R, v_L)

		return self.x, self.y, self.theta

	def reset(self,x_init:float=0,y_init:float=0,theta_init:float=0):
		"""
		車の位置と姿勢をリセットする

		Parameters
		----------
		x_init : float, optional
			 初期化後のx座標, by default 0
		y_init : float, optional
			 初期化後のy座標, by default 0
		theta_init : float, optional
			 初期化後の姿勢, by default 0
		"""
		self.x = x_init
		self.y = y_init
		self.theta = theta_init

MPC用に状態方程式を線形近似

前述の状態方程式を$dt$間隔で離散化すると、

\begin{aligned}
x_{t+1} &= x_t + v_t \cos \theta_t dt \\
y_{t+1} &= y_t + v_t \sin \theta_t dt \\
\theta_{t+1} &= \theta_t + \omega_t dt
\end{aligned} 

を得ます。上の状態方程式は非線形であるので、これをMPC用に線形化していきます。
いま、軌道追従制御を考えるので、追従させたい軌道（参照軌道）$x^{(\mathrm{ref})}_t, y_t^{(\mathrm{ref})},\theta_t^{(\mathrm{ref})}$が与えられているとします。
離散化した状態方程式を参照軌道の周りでテイラー展開して線形化すると、

\begin{aligned}
x_{t+1} &= x_{t} + v_t \cos \theta^{(\mathrm{ref})}_{t} dt - v_t \sin \theta^{(\mathrm{ref})}_{t} (\theta_t-\theta^{(\mathrm{ref})}_{t}) dt + \mathcal{O}(dt^2) \\
y_{t+1} &= y_{t} + v_t \sin \theta^{(\mathrm{ref})}_{t} dt + v_t \cos \theta^{(\mathrm{ref})}_{t} (\theta_t-\theta^{(\mathrm{ref})}_{t}) dt + \mathcal{O}(dt^2) \\
\theta_{t+1} &= \theta_{t} + \omega_t dt
\end{aligned}

となります。制御量と状態の積$v_t \theta_t$があるため状態方程式は未だに非線形です。この部分を線形化するために、$v_t$を微小量$u_t$と参照量$v_t^{(\mathrm{ref})}$に分離して、微小量$u_t$を操作量とすることを考えます。つまり、$$v_t = v_t^{(\mathrm{ref})}+ u_t$$とし、制御量$u_t$が微小であると仮定します。この変形を状態方程式に代入して2次微小量である$u_t(\theta_t-\theta^{(\mathrm{ref})}_{t})$を$0$と近似することで、

\begin{aligned}
x_{t+1} &= x_{t} + (v^{(\mathrm{ref})}_{t} + u_t) \cos \theta^{(\mathrm{ref})}_{t} dt - v^{(\mathrm{ref})}_{t} \sin \theta^{(\mathrm{ref})}_{t} (\theta_t-\theta^{(\mathrm{ref})}_{t}) dt + \mathcal{O}(dt^2) \\
y_{t+1} &= y_{t} + (v^{(\mathrm{ref})}_{t} + u_t) \sin \theta^{(\mathrm{ref})}_{t} dt + v^{(\mathrm{ref})}_{t} \cos \theta^{(\mathrm{ref})}_{t} (\theta_t-\theta^{(\mathrm{ref})}_{t}) dt + \mathcal{O}(dt^2) \\
\theta_{t+1} &= \theta_{t} + \omega_t dt
\end{aligned}

となります。ここで、参照量$v_t^{(\mathrm{ref})}$は与えられていないので、参照軌道から、

v_t^{(\mathrm{ref})}\approx \frac{\sqrt{\left(x_{t}^{(\mathrm{ref})}-x_{t-1}^{(\mathrm{ref})}\right)^2+\left(y_{t}^{(\mathrm{ref})}-y_{t-1}^{(\mathrm{ref})}\right)^2}}{dt}

と近似的に求めることにします。これらの一連の変形によって、状態方程式を制御量$u_t,\omega_t$と状態量$x_t,y_t,\theta_t$に関して線形にできました。変形後の状態方程式を整理するために、

\begin{aligned}
\bm{x}_t = \begin{bmatrix}
x_{t} \\
y_{t} \\
\theta_{t}
\end{bmatrix},\;
\bm{u}_t = \begin{bmatrix}
u_{t} \\
\omega_{t}
\end{bmatrix}
\end{aligned}

とおいて、状態方程式を整理すると、

\begin{aligned}
\bm{x}_{t+1}
=
\begin{bmatrix}
1 & 0 & -v^{(\mathrm{ref})}_{t} \sin \theta^{(\mathrm{ref})}_{t} dt \\
0 & 1 & v^{(\mathrm{ref})}_{t} \cos \theta^{(\mathrm{ref})}_{t} dt \\
0 & 0 & 1
\end{bmatrix}
\bm{x}_{t}
&+
dt
\begin{bmatrix}
\cos \theta^{(\mathrm{ref})}_{t} & 0 \\
\sin \theta^{(\mathrm{ref})}_{t} & 0 \\
0 & 1
\end{bmatrix}
\bm{u}_{t}\\
&+
v_t^{(\mathrm{ref})} dt
\begin{bmatrix}
\cos \theta^{(\mathrm{ref})}_{t} + \sin \theta^{(\mathrm{ref})}_{t} \theta^{(\mathrm{ref})}_{t} \\
\sin \theta^{(\mathrm{ref})}_{t} - \cos \theta^{(\mathrm{ref})}_{t} \theta^{(\mathrm{ref})}_{t} \\
0
\end{bmatrix}
\end{aligned}

となります。
本来の制御量は$v_{R},v_{L}$であったので、これらを基準と微小量に分離し、微小変化をMPCで計算する制御量とするために、$$v_{Rt} =v_{t}^{(\mathrm{ref})} + u_{Rt},\space v_{Lt} = v_{t}^{(\mathrm{ref})} + u_{Lt}$$とおきます。この操作により制御量が$u_{Rt}, u_{Lt}$となります。制御量を行列で

\bm{w}_t = \begin{bmatrix}u_{Rt} \\ u_{Lt}\end{bmatrix}

とすれば、

\begin{aligned}
\bm{u}_t 
 =& \begin{bmatrix}
      u_{t} \\
      \omega_{t}
   \end{bmatrix}
   =
   \begin{bmatrix}
      \frac{v_{Rt} + v_{Lt}}{2}  - v_t^{(\mathrm{ref})} \\
      \frac{v_{Rt}-v_{Lt}}{2l} \cos \alpha 
\end{bmatrix}
   =
   \begin{bmatrix}
      \frac{(v_{Rt} - v_t^{(\mathrm{ref})}) + (v_{Lt}- v_t^{(\mathrm{ref})})}{2}\\
      \frac{(v_{Rt} - v_t^{(\mathrm{ref})})-(v_{Lt}- v_t^{(\mathrm{ref})})}{2l} \cos \alpha 
   \end{bmatrix}
   = 
   \begin{bmatrix}
      \frac{u_{Rt} + u_{Lt}}{2}\\
      \frac{u_{Rt} - u_{Lt}}{2l} \cos \alpha 
   \end{bmatrix} \\
   =&
   \begin{bmatrix}
      1/2 & 1/2 \\
      \cos \alpha/(2l) & -\cos \alpha/(2l) 
   \end{bmatrix}
   \begin{bmatrix}
      u_{Rt} \\
      u_{Lt}
   \end{bmatrix}
   =\begin{bmatrix}
      1/2 & 1/2 \\
      \cos \alpha/(2l) & -\cos \alpha/(2l) 
   \end{bmatrix}\bm{w}_t 
\end{aligned}

となります。上式を用いて状態方程式を書き換えると、

\begin{aligned}
\bm{x}_{t+1}
&=
\begin{bmatrix}
1 & 0 & -v^{(\mathrm{ref})}_{t} \sin \theta^{(\mathrm{ref})}_{t} dt \\
0 & 1 & v^{(\mathrm{ref})}_{t} \cos \theta^{(\mathrm{ref})}_{t} dt \\
0 & 0 & 1
\end{bmatrix}
\bm{x}_{t}
+
dt
\begin{bmatrix}
\cos \theta^{(\mathrm{ref})}_{t} & 0 \\
\sin \theta^{(\mathrm{ref})}_{t} & 0 \\
0 & 1
\end{bmatrix}
\begin{bmatrix}
   1/2 & 1/2 \\
   \cos \alpha/(2l) & -\cos \alpha/(2l) 
\end{bmatrix}
\bm{w}_t 
+
v_t^{(\mathrm{ref})} dt
\begin{bmatrix}
\cos \theta^{(\mathrm{ref})}_{t} + \sin \theta^{(\mathrm{ref})}_{t} \theta^{(\mathrm{ref})}_{t} \\
\sin \theta^{(\mathrm{ref})}_{t} - \cos \theta^{(\mathrm{ref})}_{t} \theta^{(\mathrm{ref})}_{t} \\
0
\end{bmatrix} \\
&=\begin{bmatrix}
1 & 0 & -v^{(\mathrm{ref})}_{t} \sin \theta^{(\mathrm{ref})}_{t} dt \\
0 & 1 & v^{(\mathrm{ref})}_{t} \cos \theta^{(\mathrm{ref})}_{t} dt \\
0 & 0 & 1
\end{bmatrix}
\bm{x}_{t}
+ dt
\begin{bmatrix}
   \cos \theta^{(\mathrm{ref})}_{t}/2   & \cos \theta^{(\mathrm{ref})}_{t}/2  \\
   \sin \theta^{(\mathrm{ref})}_{t}/2   & \sin \theta^{(\mathrm{ref})}_{t}/2 \\
   \cos \alpha/(2l) & -\cos \alpha/(2l)
\end{bmatrix}
\bm{w}_t
+
v_t^{(\mathrm{ref})} dt
\begin{bmatrix}
\cos \theta^{(\mathrm{ref})}_{t} + \sin \theta^{(\mathrm{ref})}_{t} \theta^{(\mathrm{ref})}_{t} \\
\sin \theta^{(\mathrm{ref})}_{t} - \cos \theta^{(\mathrm{ref})}_{t} \theta^{(\mathrm{ref})}_{t} \\
0
\end{bmatrix}
\end{aligned}

となります。この状態方程式を用いてMPCを構成していきます。

MPCの実装

制約条件の決定

制約条件として、車輪が回る速度に上限があるという状況を考えます。
つまり、入力$v_{Lt}, v_{Rt}$の絶対値が$v_{\mathrm{max}}$以下であるという制約条件を課します。
この条件を数式で表現すると

\left\{\begin{aligned}
-v_{\mathrm{max}} \leq v_{Lt} \leq v_{\mathrm{max}} \\
-v_{\mathrm{max}} \leq v_{Rt} \leq v_{\mathrm{max}}
\end{aligned}\right.
\Leftrightarrow
\left\{
\begin{aligned}
-v_{\mathrm{max}} - v_t^{(\mathrm{ref})} \leq u_{Lt} \leq v_{\mathrm{max}}- v_t^{(\mathrm{ref})} \\
-v_{\mathrm{max}}- v_t^{(\mathrm{ref})} \leq u_{Rt} \leq v_{\mathrm{max}}- v_t^{(\mathrm{ref})}
\end{aligned}\right.

となります。

目的関数の決定

目的関数$J$は、軌道追従誤差の二乗和とします。これにより、参照軌道とロボットの実際の軌道が一致したときに目的関数が最小になるので、ロボットの軌道が参照軌道に一致するような制御量が得られることが期待できます。

\begin{aligned}
J = \sum_{t=0}^{T-1} \left( \left( x_{t} - x^{(\mathrm{ref})}_{t} \right)^2 + \left( y_{t} - y^{(\mathrm{ref})}_{t} \right)^2 + \left( \theta_{t} - \theta^{(\mathrm{ref})}_{t} \right)^2 \right)
\end{aligned}

ここで、$T$は予測ホライズンです。

実装

以上の線形状態方程式・制約条件・目的関数を用いて、MPCを作成すると以下になります。ここで、2次凸計画問題を解くのには、pythonのcvxpyパッケージを利用しました。

class ModelPredictiveController:
    def __init__(self, wheel_length: float, wheel_angle: float, dt: float, v_max: float):
        """
        コンストラクタ

        Parameters
        ----------
        length : float
            車輪間距離
        alpha : float
            車輪配置角度
        dt : float
            離散時間間隔
        v_max : float
            許容最大速度
        """
        self.length = wheel_length
        self.alpha = wheel_angle
        self.dt = dt
        self.v_max = v_max        
    
    def calc_At(self, x_target: float, y_target: float,v_target: float,theta_target: float) -> np.ndarray:
        At = np.array(
            [
                [1, 0, -self.dt * np.sin(theta_target) * v_target],
                [0, 1, self.dt * np.cos(theta_target) * v_target],
                [0, 0, 1],
            ]
        )
        return At
    
    def calc_Bt(self, x_target: float, y_target: float,v_target: float, theta_target: float) -> np.ndarray:
        Bt = self.dt/2 * np.array(
            [
                [np.cos(theta_target), np.cos(theta_target)],
                [np.sin(theta_target), np.sin(theta_target)],
                [np.cos(self.alpha)/self.length, -np.cos(self.alpha)/self.length],
            ]
        )
        return Bt
    
    def calc_Ct(self, x_target: float, y_target: float,v_target: float, theta_target: float) -> np.ndarray:
        Ct = v_target * self.dt* np.array(
            [
                [np.cos(theta_target)+np.sin(theta_target)*theta_target],
                [np.sin(theta_target)-np.cos(theta_target)*theta_target],
                [0]
            ]
        )
        return Ct
    
    def calc_U(self,X_0,X_target:np.array)->np.ndarray:
        """
        最適化問題を解いて制御量の時系列を求める

        Parameters
        ----------
        X_0 : np.ndarray
            現在の状態[x,y,theta]
        X_target : np.ndarray
            追従軌跡。shape[3,horizon+1]
        Returns
        -------
        np.ndarray
            制御量の時系列。shape[2,horizon]
        """
        # 予測ホライズンの長さを取得
        horizon = X_target.shape[1] - 1
        
        # 変数
        X = cp.Variable((3, horizon+1)) # 状態変数(微少量)
        W = cp.Variable((2, horizon)) # 入力変数
        
        V_target = np.linalg.norm(np.diff(X_target[0:2,:]),axis=0,ord=2)/self.dt # 速度
        
        # 制約
        constraints = [X[:,0] == X_0] # 初期値
        for t in range(horizon):
            At = self.calc_At(X_target[0,t],X_target[1,t],V_target[t],X_target[2,t])
            Bt = self.calc_Bt(X_target[0,t],X_target[1,t],V_target[t],X_target[2,t])
            Ct = self.calc_Ct(X_target[0,t],X_target[1,t],V_target[t],X_target[2,t])
            constraints += [X[:,t+1,None] == At@X[:,t,None]+Bt@W[:,t,None]+Ct,
                            cp.abs(W[0,t] + V_target[t]) <= self.v_max,
                            cp.abs(W[1,t] + V_target[t]) <= self.v_max]
        
        # コスト関数
        cost = cp.sum_squares(X - X_target)
        # 最適化
        prob = cp.Problem(cp.Minimize(cost), constraints)
        prob.solve()
        
        solution = np.array(W.value)
        solution[0:2,:] = solution[0:2,:] + V_target[None,:] # 速度を足して実際の速度にする
        
        return solution

実験

カージオイド軌道追従

上記のMPCの動作確認のために、カージオイド軌道を追従させてみます。
カージオイドの軌跡は、

\begin{aligned}
x^{(\mathrm{ref})}_{t} &= a(2 \cos \omega t - \cos 2 \omega t)\\
y^{(\mathrm{ref})}_{t} &= a(2 \sin  \omega t - \sin 2 \omega t)\\
\theta^{(\mathrm{ref})}_{t} &= \tan^{-1} \left( \frac{\cos  \omega t - \cos 2 \omega t}{-\sin  \omega t + \sin 2 \omega t} \right)
\end{aligned}

で与えられます。ここで、$a$はスケールを表すパラメータ、$\omega$は回転速度を表すパラメータです。カージオイドの軌跡を生成する関数は以下のようになります。

def generate_cardioid_trajectory(omega:float, scale:float,total_steps:int, dt:float)->np.ndarray:
      t = np.arange(0,total_steps*dt,dt)
      x = scale*(2*np.cos(omega*t)-np.cos(2*omega*t))
      y = scale*(2*np.sin(omega*t)-np.sin(2*omega*t))
      dx = -scale*(2*omega*np.sin(omega*t)-2*omega*np.sin(2*omega*t))
      dy = scale*(2*omega*np.cos(omega*t)-2*omega*np.cos(2*omega*t))
      theta = np.arctan2(dy,dx)
      
      #thetaが連続になるように調整
      theta = np.unwrap(theta)
      
      return np.array([x,y,theta])

今回の実験でのロボット・MPCのパラメータは以下の表としました。

パラメータ	数値
車輪間距離$l$	$0.02$ m
車輪配置角度$\alpha$	$\pi/6$ rad
タイヤの最大移動速度$v_{\mathrm{max}}$	$0.5$ m/s
予測ホライズン$T$	$10$
制御間隔$dt$	$0.1$ s

さらに、カージオイドのパラメータは以下の表としました。

パラメータ	数値
スケール$a$	$0.1$ m
回転速度$\omega$	$2\pi/10$ rad/s

以上の設定で、初期位置が参照軌道と一致している場合についてシミュレーションを行うと以下の図のようになります。赤線・赤矢印がそれぞれ参照軌跡・方向を表し、青線・青矢印が実際のロボットの軌跡・方向を表します。グラフを見ると、かなり頑張っている様子が伺えます。

次に、初期位置が参照軌道と異なっている場合（初期位置を参照軌道+0.1m）についてシミュレーションを行うと以下の図のようになります。グラフの見方は上と同じです。グラフから、初期位置がずれていても段々と参照軌道に合わせられることがわかります。

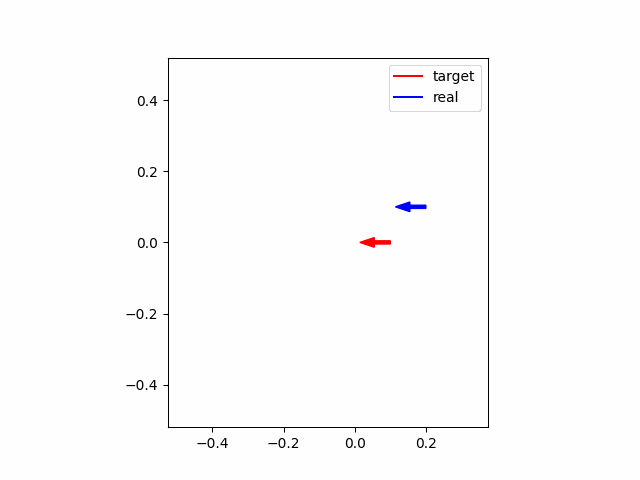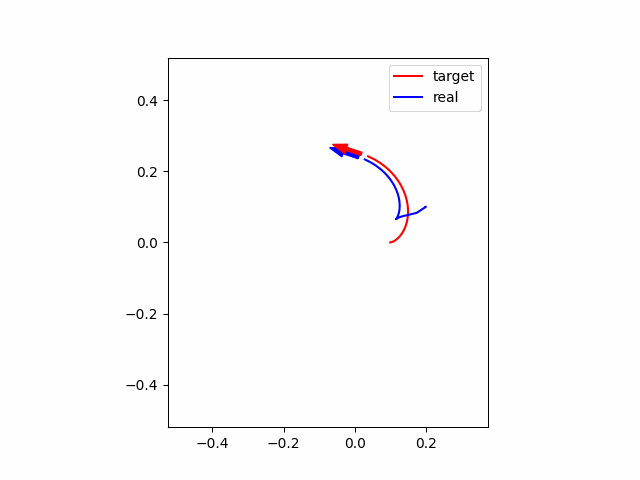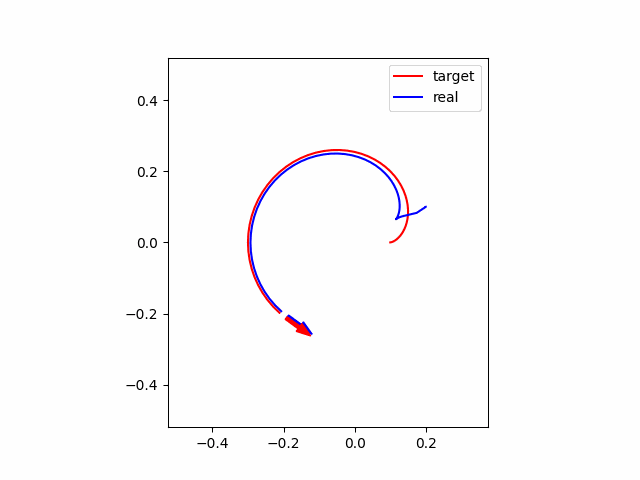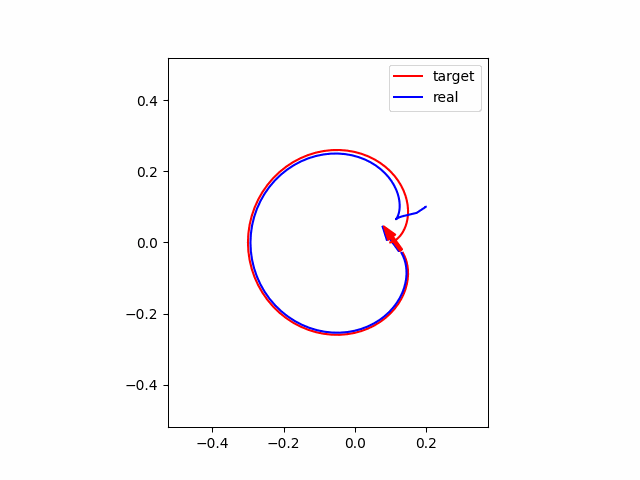
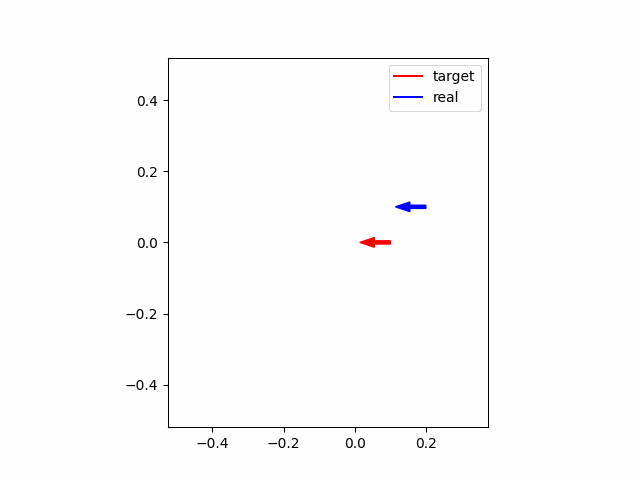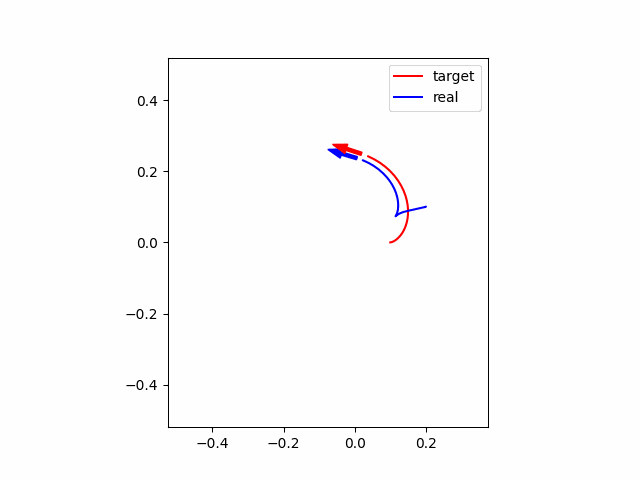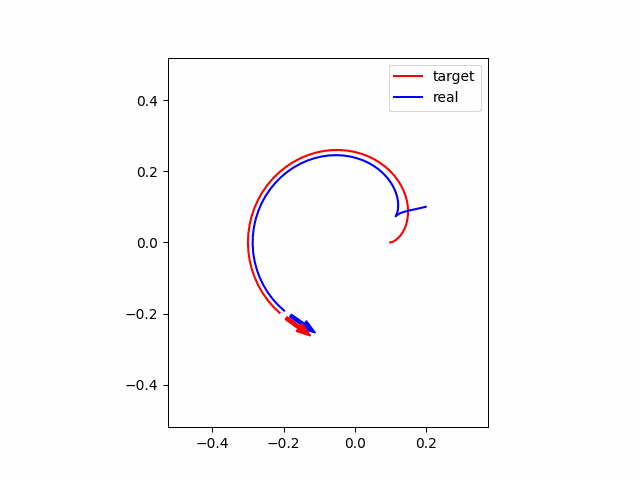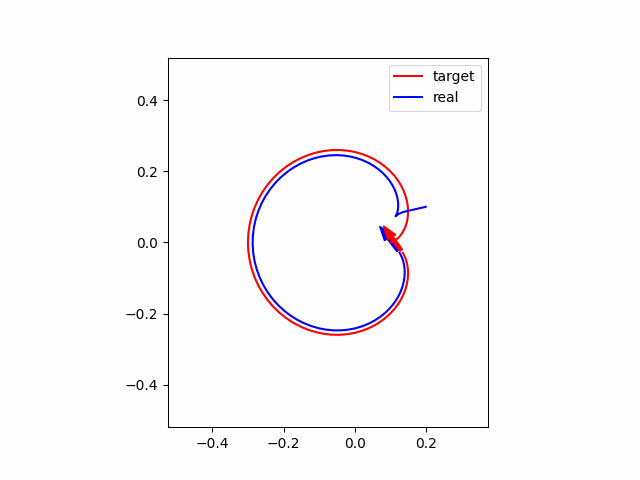
最後に、ロバスト性を確認するために、初期位置が上と同様に異なっていて、かつMPCに設定した車輪のパラメータがそれぞれ$l=0.02\times0.8 $ m、車輪配置角度$\alpha = \pi/6\times0.8$ rad　と2割のモデル誤差がある場合について、シミュレーションをしてみます。シミュレーション結果は以下の通りです。グラフから、残差は残ってしまっていますが、かなり追従できていることがわかります。

まとめ

MPCを使って対向2輪型移動ロボットの軌道追従制御を行ってみました。
ロバストかつ初期位置がずれててもうまく追従してくれるのすごいです。
今回は非線形方程式を線形近似して取り扱ったので、次回は（あれば）非線形MPCに挑戦してみようと思います。