最近流行りつつある科学計算処理向けの高水準言語「Julia」の基本操作をまとめていきます。
1.準備編
2.確率分布・仮説検定と可視化編
3.データフレーム操作編
chapter.0 利用環境の準備
1.Julia install
Macユーザー向けです。
Juliaをインストールするには、公式サイトhttp://www.julialang.org からディスクイメージ(.dmg)をダウンロードし、内容をアプリケーション・フォルダにコピーするだけです。インストールしたJulia.appを起動すると、ターミナルの中でJuliaが立ち上がり、すぐに利用開始できます。
brew があればターミナルから以下が簡単です。
$ brew cask install julia
2.起動
ターミナルから以下で起動( "Julia-1.2" の箇所は install 時のバージョンを入れる)
$ /Applications/Julia-1.2.app/Contents/Resources/julia/bin/julia
PATHを通す
$ export PATH=${PATH}:/Applications/Julia-1.2.app/Contents/Resources/julia/bin
$ source .bash_profile
起動してみる
$ julia
_
_ _ _(_)_ | Documentation: https://docs.julialang.org
(_) | (_) (_) |
_ _ _| |_ __ _ | Type "?" for help, "]?" for Pkg help.
| | | | | | |/ _` | |
| | |_| | | | (_| | | Version 1.2.0 (2019-08-20)
_/ |\__'_|_|_|\__'_| | Official https://julialang.org/ release
|__/ |
julia>
3.juliaの各種モードとjupyter notebookでの利用
juliaはいくつかモードがあって、それを切り替えながら使用します。
まずは、jupyter notebook で使用するために IJulia パッケージを install してみたいと思います。
パッケージ isntall
まずターミナルから julia 起動
$ julia
で " ] " と入力すると
(v1.2)pkg>
上記のようにパッケージ管理などを行える REPL モードに移るので
(v1.2)pkg> add IJulia
で IJulia の install ができます。これだけで jupyter notebook で使用する準備はOKです。
※jupyter notebook 未 install の方は install しましょう。
なお、Anaconda から jupyter を install した方は設定方法が異なるかも。ご注意を
念のため jupyter の kernel 一覧を確認してみると...
$ jupyter kernelspec list
Available kernels:
julia-1.2 /Users/xxxx/Library/Jupyter/kernels/julia-1.2
なお、install 済みパッケージの確認は "st" コマンドで。
(v1.2)pkg> st
Status `~/.julia/environments/v1.2/Project.toml`
[xxxxxxxx] IJulia v1.20.2
ちなみに各種パッケージやライブラリのinstallはこのREPLモードで行うようです。
他にもモードがあるので、ちょっと紹介。
shell モード
その名の通りですが、shell (bash)入力が可能なモード
$ julia
で、" ; "と入力。
shell>
ためしに、
shell> pwd
/Users/xxxx
こんな感じ。
helpモード
Rの "?" や python の "help()" に相当するモード
$ julia
で、" ? "と入力。
help?>
ためしに、
help?> sum
## ドキュメント
こんな感じ。
jupyter notebook でのモード切り替え

chapter.1 基本操作
1.基本的な算術
julia> 1 + 2 + 3
6
julia> 1 - 2
-1
julia> 3 * 2 / 12
0.5
julia> 3 ^ 2 # 3の二乗 Excelっぽい
9
julia> x = 1
1
julia> x += 4
5
julia> x % 3
2
julia> div(17, x) # python で言う所の 17//5
3
julia> x = 2 ; y = 3 # 一行で複数の変数を定義することも
3
julia> x + y
5
julia> z = (x = 1; y = 2; x + y) # このような記述方法もある
3
2.配列
julia> [1 2 3]
1×3 Array{Int64,2}:
1 2 3
julia> Int64[1 2 3] # 配列の型指定
1×3 Array{Int64,2}:
1 2 3
julia> Float64[1 2 3]
1×3 Array{Float64,2}:
1.0 2.0 3.0
julia> String["A" "B" "C"]
1×3 Array{String,2}:
"A" "B" "C"
julia> Any[1 "A"]
1×2 Array{Any,2}:
1 "A"
julia> size([1 2 3 4 5]) # pandas の".shape"や R の"dim"に相当
(1, 5)
julia> length([1 2 3 4 5]) # python の "len()"に相当
julia> a = [1 2 3 4 5]
julia> a[1] # index は 1 から
1
julia> a[[2 4]] # 複数 index
1×2 Array{Int64,2}:
2 4
julia> a[1:3] スライス
3-element Array{Int64,1}:
1
2
3
julia> maximum(a)
5
julia> minimum(a)
1
julia> sum(a)
15
julia> A = [1 2 3 ; 4 5 6] # 行列
2×3 Array{Int64,2}:
1 2 3
4 5 6
# 以下も同じ意味
# A = [1 2 3
# 4 5 6]
julia> A' # 転置
3×2 Adjoint{Int64,Array{Int64,2}}:
1 4
2 5
3 6
julia> A[5] # 次元数を気にせず一つのindexで要素アクセス。Rのmatrixっぽい
3
julia> A[:, 2] # index指定。numpy,Rっぽい
2-element Array{Int64,1}:
2
5
3.ベクトルの演算
julia> a = [1 2 3] ; b = [4 5 6]
julia> a + b
1×3 Array{Int64,2}:
5 7 9
julia> a - b
1×3 Array{Int64,2}:
-3 -3 -3
julia> a .* b # a * b ではない点に注意
1×3 Array{Int64,2}:
4 10 18
julia> a .+ 1
1×3 Array{Int64,2}:
2 3 4
julia> a .* 5
1×3 Array{Int64,2}:
5 10 15
線形代数のパッケージもある
なお、ライブラリの import は using [ライブラリ名称]
julia> using LinearAlgebra
julia> dot(a ,b) # 内積
32
julia> cosineθ = dot(a, b) / (sqrt(dot(a, a)) * sqrt(dot(b, b)))
0.9746318461970762
他の配列データ型
julia> tuple(1,2) # python と一緒
(1,2)
julia> Set([1 1 2 3 4 4]) # 集合 S が大文字!!
Set([4, 2, 3, 1])
julia> my_profile = Dict([("name", "Hiro"), ("age", 35)]) # 辞書
Dict{String,Any} with 2 entries:
"name" => "Hiro"
"age" => 35
julia> my_profile = Dict("name" => "Hiro", "age" => 35) # これも一緒
Dict{String,Any} with 2 entries:
"name" => "Hiro"
"age" => 35
julia> user_profile["name"]
"Hiro"
その他
julia> π
π = 3.1415926535897...
julia> ℯ
ℯ = 2.7182818284590...
julia> 1 / (1 + ℯ^-2)
0.8807970779778823
julia> x = [1 2 3 4] # 配列の場合
julia> 1 ./ (1 .+ ℯ.^-x) # 演算子の先頭に . を付ける
1×4 Array{Float64,2}:
0.731059 0.880797 0.952574 0.982014
julia> 日本語変数もできる = 10
10
julia> 日本語変数もできる + 1
11
4.制御フロー
ここからは jupyter notebook



for文
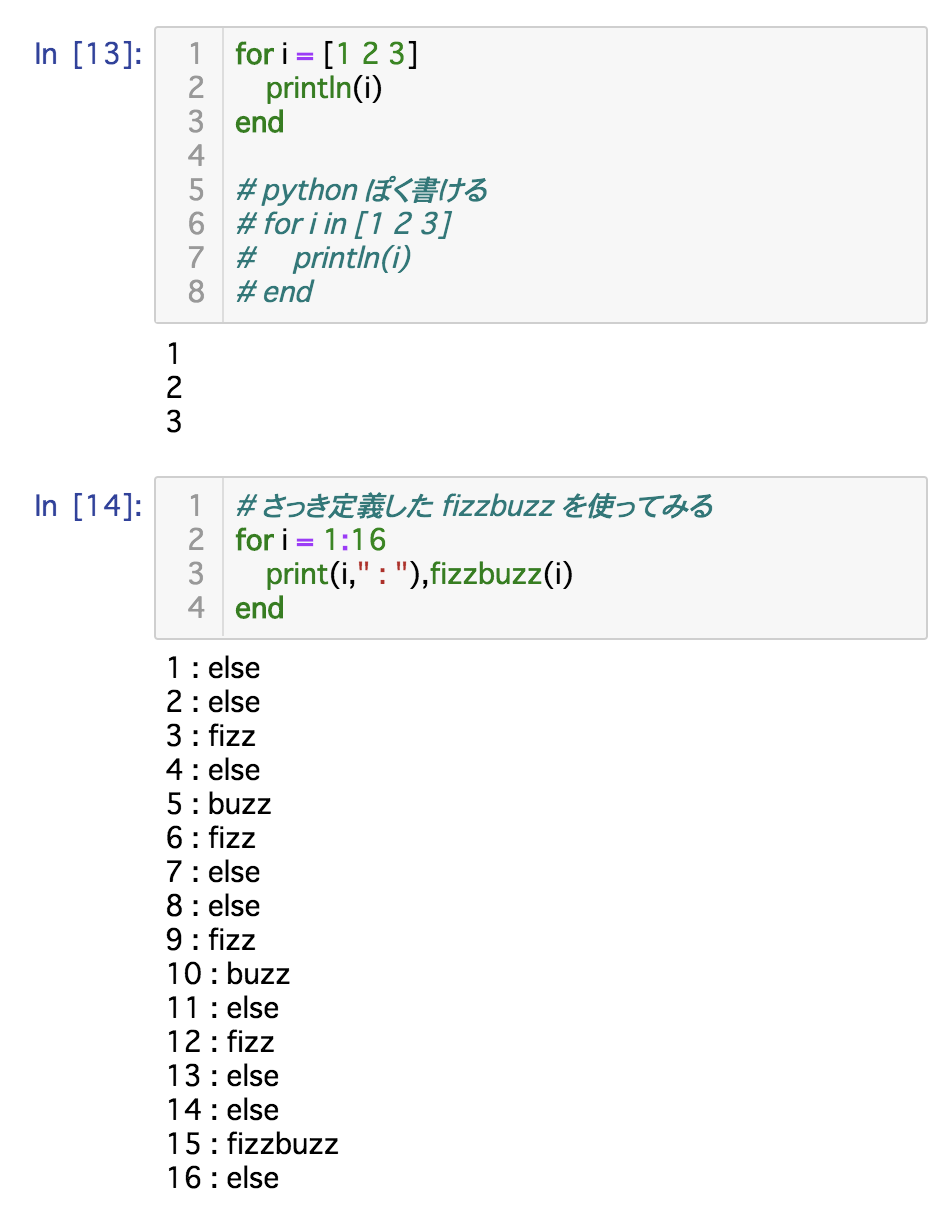



関数

※思いの外、量が多くなってしまったので、何回かに分けます。次回は確率分布と可視化の予定
