はじめてのNN実装：MATLAB/Simulinkでゼロから作るシンプルXORニューラルネットワーク入門

1. イントロダクション

この記事では、MATLABとSimulinkを使って、ゼロからニューラルネットワーク (NN) を実装し、シンプルなXOR問題を解く方法を学びます。既存のライブラリや転移学習に頼らず、未学習の状態から自分でNNをトレーニングする過程を、実際のコードとSimulinkモデルの例を交えて解説していきます。
すでに大規模データセットで事前学習されたモデルを使う「転移学習」は非常に強力ですが、本記事では 0から実装する過程と学習の仕組みを深く理解することを目的としています。

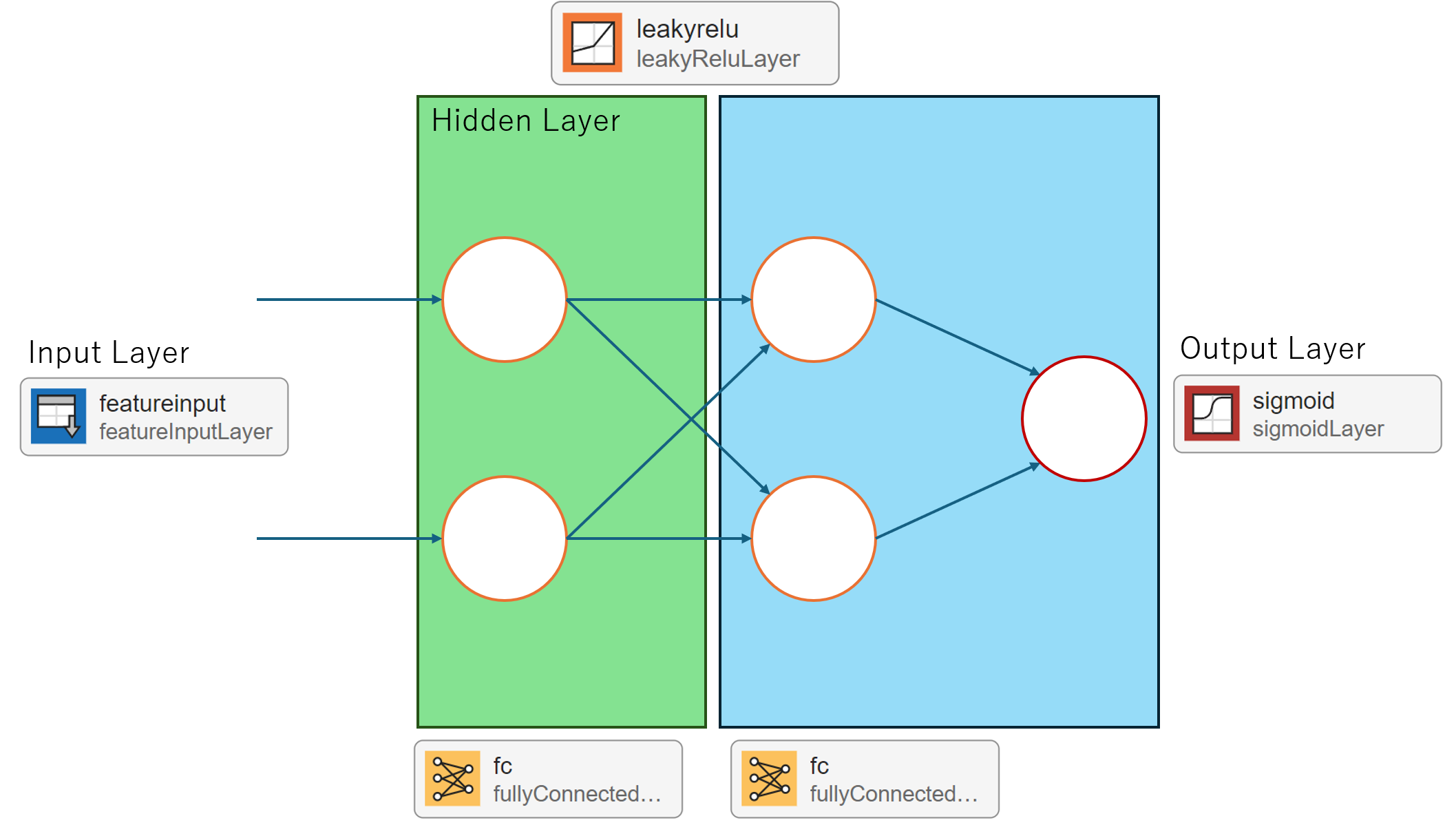
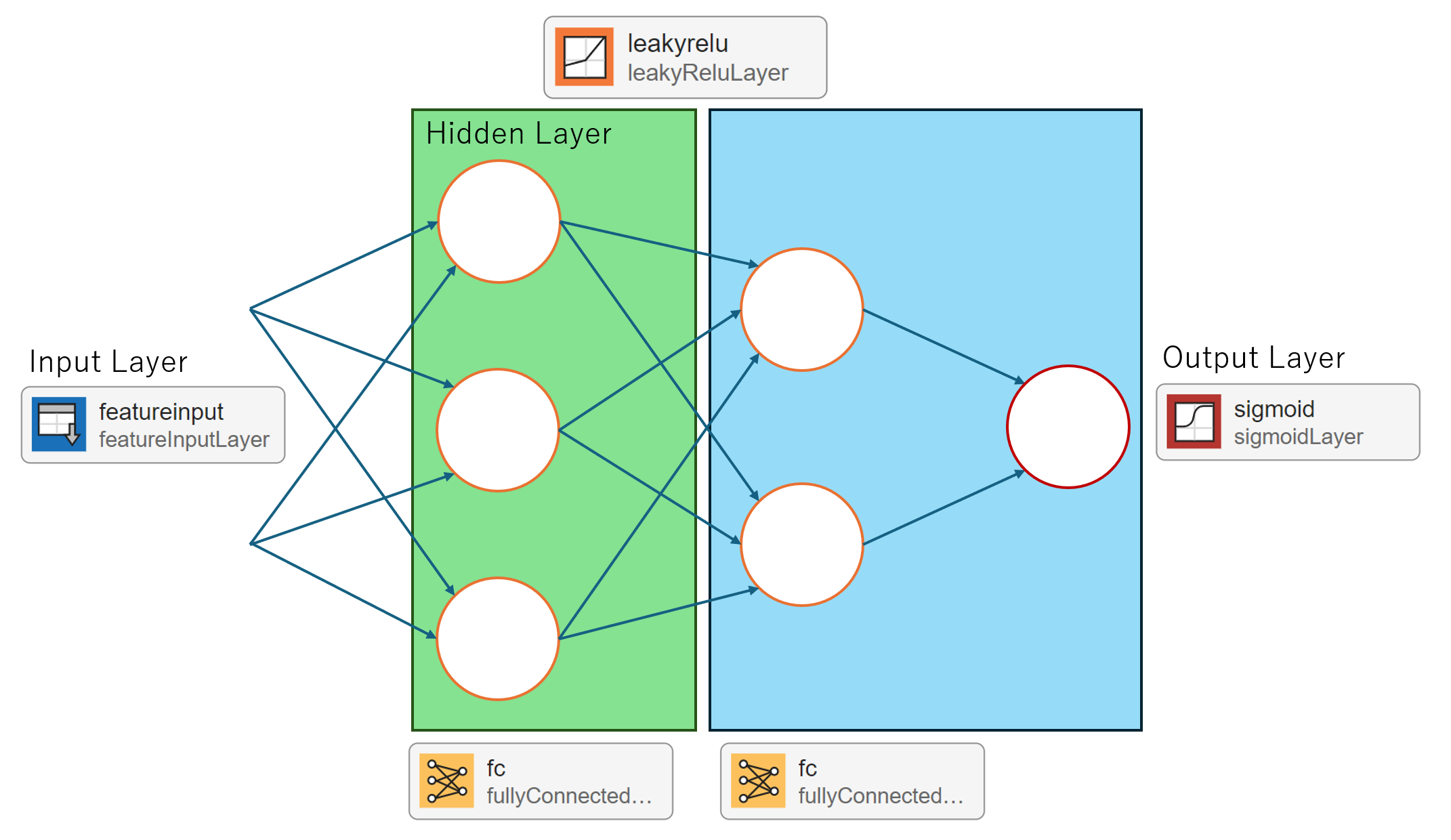
このチュートリアルでは、理論上は最小限の構造（入力層2、隠れ層2、出力層1）でXORは解けるとされていますが、実践的な学習では局所最適解に陥りやすい問題が発生するため、再現性の向上を狙って隠れ層のニューロン数を3個に増やした構造（2-3-1構造）を採用します。

1.1. 必要な環境

この記事の内容を実践するには、以下のソフトウェアのライセンスが必要です：

• MATLAB
• Simulink
• Deep Learning Toolbox

各ソフトウェアはMathWorksの公式サイトから入手可能です。ご利用の際は、適切なライセンスがあることをご確認ください。

1.2. 対象読者

• ニューラルネットワークに興味はあるが、まだ実装経験がない初心者の方
• MATLABやSimulinkを使って実際に手を動かしながら学びたいエンジニアや学生の方
• 理論だけでなく、実践的なスキルを身につけ、学んだ内容をすぐに試してみたいと考えている方

1.3. 学習の流れの概略

この記事では、以下のステップで進めていきます：

1. XOR問題の理解:
   XOR問題がなぜニューラルネットワーク学習の良い題材となるのか、その基礎知識と背景を解説します。

2. シンプルなNNによる理論的背景:
   理論上は最小限の構造でXORを解くことが可能ですが、実際の学習では局所最適解に陥りやすいという課題があります。そこで、入力層2、隠れ層3、出力層1の構造（2-3-1構造）を採用し、隠れ層の活性化関数を勾配の流れが改善されるleakyReLUを採用することで、より再現性のある学習を目指します。

3. MATLABでのNN実装:
   Deep Network Designerやコード例を通じて、NNの構築・トレーニング手法をステップバイステップで解説します。

4. Simulinkでの統合と検証:
   実装したNNをSimulinkに組み込み、シミュレーション環境で動作を確認する方法を説明します。

5. まとめと今後の展望:
   今回の内容を振り返り、さらに深い学習や応用へのステップをご提案します。

1.4. このチュートリアルで得られるもの

• 基礎から実践へ:
  自分で最初からNNを構築し、トレーニングするプロセスを体験できます。これにより、ニューラルネットワークの内部動作や学習の仕組みを深く理解し、応用力を養うことができます。

• シンプルXOR問題による理論と実践の融合:
  XOR問題は、線形分離不可能な代表例として知られており、シンプルなネットワーク構造で非線形問題を解く手法を学ぶことができます。ここでは、再現性の向上を目指して、隠れ層のニューロン数を3個に増やし、活性化関数をleakyReLUに変更した構造で学習を行います。

• 手を動かして学ぶ実践型チュートリアル:
  記事内のコード例やSimulinkのブロック図を参考に、実際に自分の環境で再現してみることで、理論だけでなく実践的なスキルも同時に身につけることができます。

• すぐに試せる実践環境:
  記事内で紹介するコードやSimulinkモデルはGitリポジトリにアップロード済みです。読者は手元の環境で実際に動かして検証することができ、学んだ内容をすぐに実践に生かせます。

さあ、一緒にゼロから始めるNN実装の世界へ、一歩踏み出してみましょう！

2. XORとは何か

XOR（排他的論理和）は、2つの入力が与えられた場合に、一方のみが真 (1) であれば出力が真となり、両方が同じ値の場合は偽 (0) になる論理ゲートです。具体的には、以下の真理値表で示されるように、入力の組み合わせによって出力が決まります。

入力A	入力B	出力 (A XOR B)
0	0	0
0	1	1
1	0	1
1	1	0

この性質から、XORは「線形分離不可能」な問題として有名です。すなわち、データ点を2次元の平面にプロットしたとき、単純な直線や平面ではクラスを完全に分けることができません。以下の図は、XOR問題における各データ点の分布を示しています。

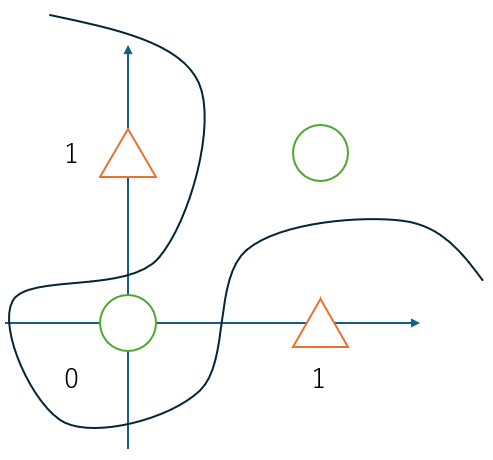
図の説明:
上記の図は、XOR問題におけるデータ点の分布を示しています。

• 緑の丸は出力が0となる組み合わせ（(0,0) および (1,1)）を表し、
• オレンジの三角は出力が1となる組み合わせ（(0,1) および (1,0)）を表しています。

図からわかるように、緑の丸とオレンジの三角が交互に配置されており、直線では両クラスを完全に分割することができません。しかし、もしも曲線のような非線形な境界を用いれば、各クラスをうまく分割することが可能です。ニューラルネットワークは、隠れ層における非線形な活性化関数を通して、曲線的な決定境界を学習することで、XOR問題のような線形分離不可能な問題にも対応できるのです。

3. シンプルなNNでXORを解く理論的背景

ニューラルネットワークの学習を理解するためには、まず可能な限りシンプルなモデルから始めることが効果的です。理論上は、入力層2、隠れ層2、出力層1という最小構成でXORは解けるとされていますが、実際のトレーニングでは局所最適解に陥りやすいという課題があります。そこで、実践で再現性のある学習を目指すため、以下の工夫を行いました。

• ネットワーク構造の拡張:
  従来の隠れ層ニューロン2個から、隠れ層ニューロンを3個に増やします（2-3-1構造）。これにより、ネットワークの表現力が向上し、柔軟な非線形変換が可能になるため、局所最適解に陥りにくくなります。

この変更により、シンプルな2層構造（厳密には隠れ層1層＋出力層）であっても、XORの正しいマッピング（[0 1 1 0]）に再現性をもって収束させる可能性が高まります。
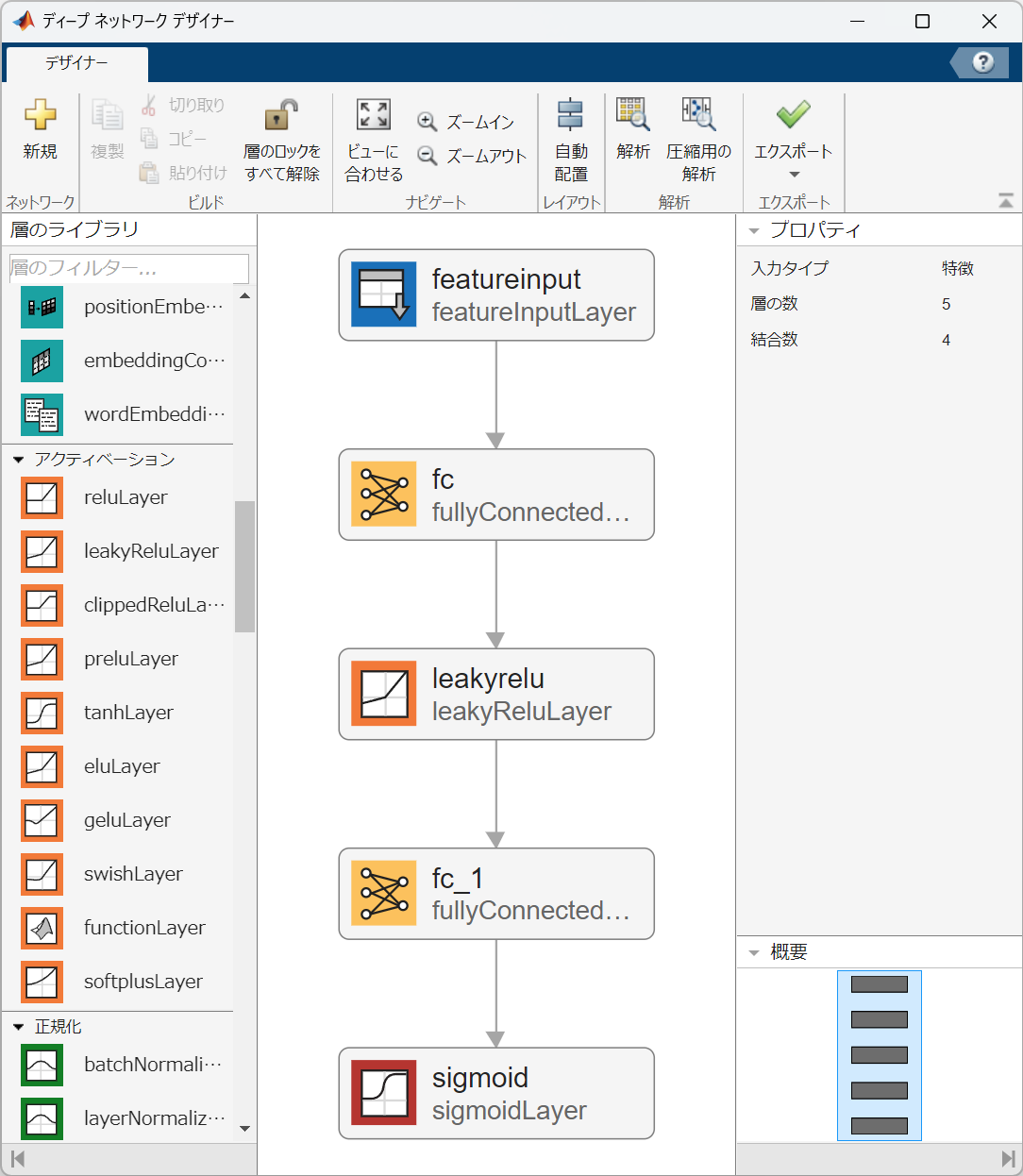
下記の図は、変更後のネットワーク構造（入力層2、隠れ層3、出力層1）を示しています。

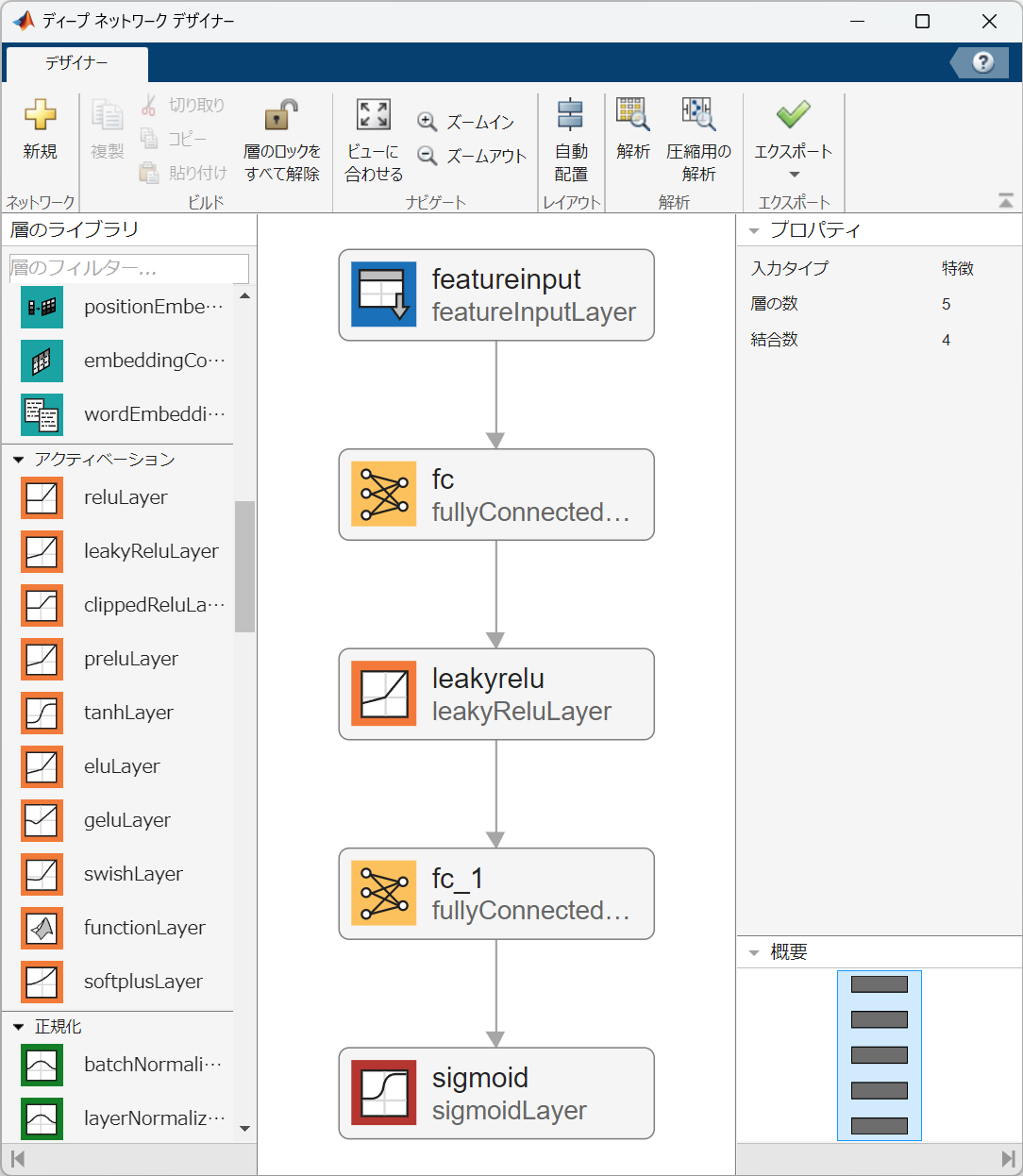
4. MATLAB/Deep Network DesignerによるNN実装

MATLABのDeep Network Designerを使えば、視覚的にニューラルネットワークの構築・編集が可能です。ここでは、XOR問題を解くためのネットワークを、以下の手順で作成します。

手順

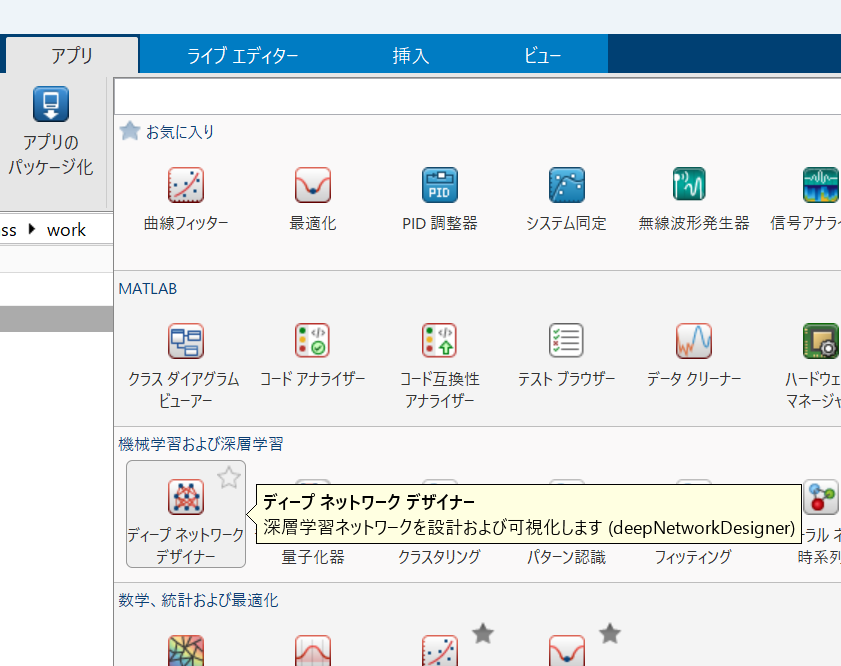
1. MATLABを起動
   MATLABを起動し、上部メニューのアプリタブをクリックします。

2. ディープネットワークデザイナーの起動
   アプリ一覧からディープネットワークデザイナーを選択します。すると、グラフィカルなネットワーク構築画面が表示されます。
   

3. ネットワークの構成
   以下の順に層を追加して、ネットワークを構成します。

   • featureInputLayer

     • 名前: featureinput
     • InputSize: 2
       この層は、XOR問題の2次元入力（例: [0;0], [0;1], [1;0], [1;1]）を受け取ります。

   • fullyConnectedLayer

     • 名前: fc
     • OutputSize: 3
       ここでは、隠れ層のニューロン数を3に設定します。

   • leakyReluLayer

     • 名前: leakyrelu
       隠れ層で線形変換された値に対し、leakyReLU活性化関数を適用して非線形変換を行います。これにより、学習の安定性が向上します。

   • fullyConnectedLayer

     • 名前: fc_1
     • OutputSize: 1
       隠れ層の出力を1つのニューロンに変換し、最終出力を生成します。

   • sigmoidLayer

     • 名前: sigmoid
       出力層でシグモイド関数を適用し、出力を0～1の範囲に正規化します。

1. ネットワークの保存・エクスポート
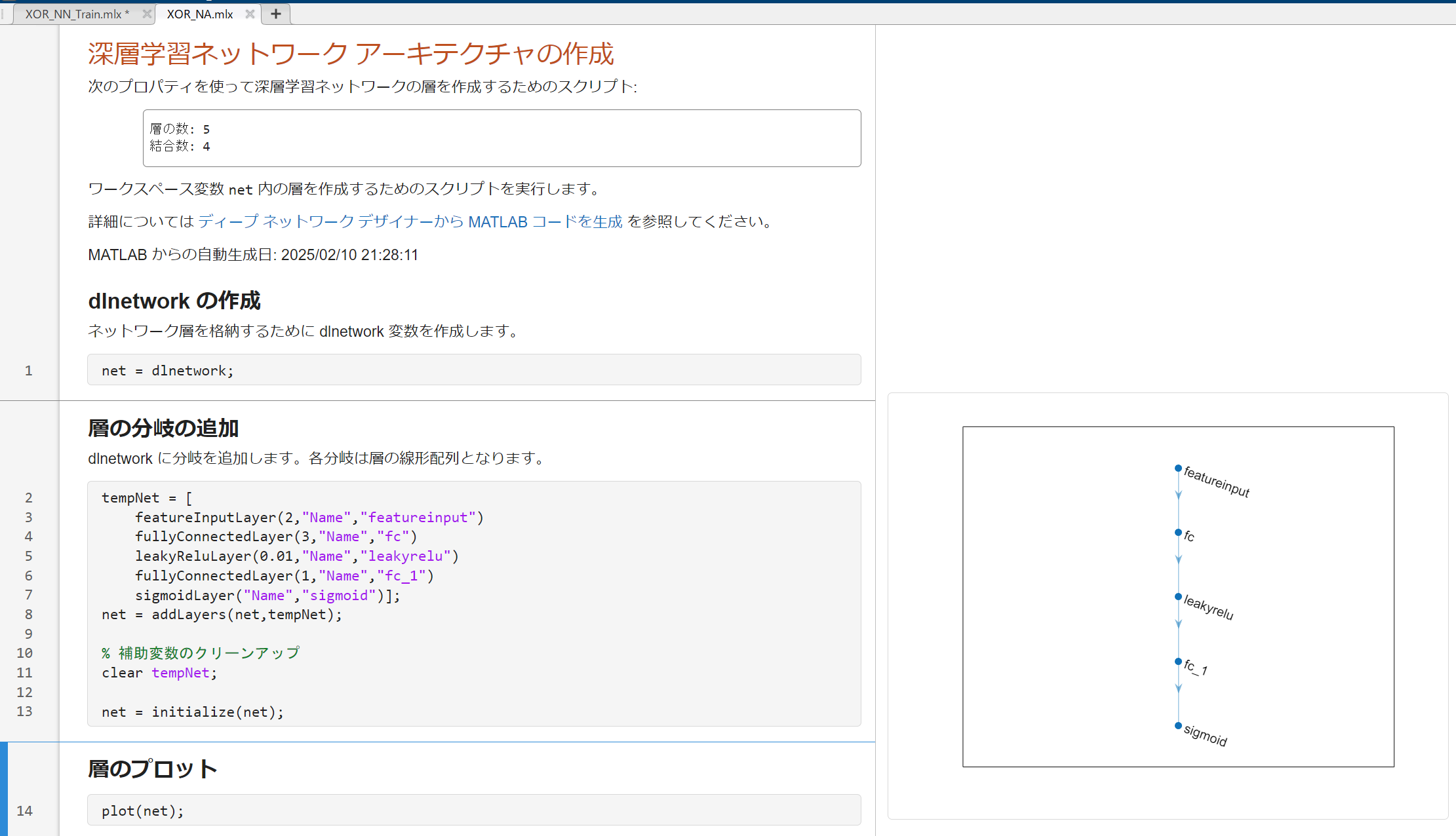
   ネットワーク構築が完了したら、エクスポート機能を利用して、パラメータなしのネットワークコードを生成します。生成したコードを実行し、ワークスペース上にネットワークを読み込みます。

5. トレーニングと評価

ここからは、作成したニューラルネットワークを使ってXOR問題の学習を行い、その結果を評価する方法を説明します。以下のコードは、MATLABでトレーニングデータの作成、トレーニングパラメータの設定、学習ループ、そして学習後の評価までの一連の流れを示しています。

---

5.1. XOR のトレーニングデータの作成

このセクションでは、XOR問題に対応するトレーニングデータを準備します。

• 入力データ (X):
  各列が1サンプルとなる2×4の行列として定義され、サンプルは [0;0], [0;1], [1;0], [1;1] です。
• ターゲットデータ (T):
  各サンプルに対する正解ラベルが1×4のベクトルとして与えられ、XORの真理値に基づいてそれぞれ 0, 1, 1, 0 が割り当てられます。

さらに、これらのデータは dlarray に変換され、'CB'（Channel × Batch）形式で格納されることで、ディープラーニングの計算に適したデータ形式になります。

X = [0 0 1 1;
     0 1 0 1];

T = [0 1 1 0];

% 入力とターゲットを dlarray に変換します。
% 'CB' 形式は、チャネル (Channel) × バッチ (Batch) という次元ラベルを指定しています。
dlX = dlarray(X, 'CB');
dlT = dlarray(T, 'CB');

5.2. トレーニングパラメータの設定

このセクションでは、トレーニングを実施するための基本的なパラメータを設定します。

• エポック数 (numEpochs):
  ネットワークの学習を繰り返す回数を指定します。多くのエポックを重ねることで、ネットワークはより最適なパラメータに近づきます。
• 学習率 (learningRate):
  各エポックで勾配降下法を用いてパラメータ更新する際のステップサイズを決定します。学習率が大きすぎると発散し、小さすぎると収束が遅くなるため、適切な値の設定が重要です。

numEpochs   = 10000;    % エポック数（学習の繰り返し回数）
learningRate = 0.1;     % 学習率

5.3. トレーニングループ

トレーニングループでは、以下の一連の手順を各エポックごとに実行します。

1. 順伝播と損失の計算:

   • 現在のネットワークパラメータを用いて、入力データから出力を計算します。
   • 予測出力とターゲットとの間で、binary cross-entropy損失を計算し、ネットワークのパフォーマンスを数値化します。

2. 勾配の計算とパラメータ更新:

   • 誤差逆伝播法を利用して、損失に対する各パラメータの勾配を求めます。
   • 得られた勾配に基づき、学習率を掛けた値を各パラメータから差し引くことで、パラメータを更新します。

3. 進捗の表示:

   • 例えば100エポックごとに現在の損失値を表示することで、学習の進行状況を確認できるようにしています。

この一連のプロセスにより、ネットワークはXOR問題の解決に向けた最適なパラメータへと更新されていきます。

for epoch = 1:numEpochs
    % modelLoss 関数を dlfeval で呼び出し、損失と勾配を計算します。
    [loss, gradients] = dlfeval(@modelLoss, net, dlX, dlT);
    
    % 各学習可能パラメータを、勾配降下法で更新します。
    % net.Learnables はテーブル形式になっているので、各行ごとに値を更新します。
    for i = 1:size(net.Learnables,1)
        net.Learnables.Value{i} = net.Learnables.Value{i} - learningRate * gradients.Value{i};
    end
    
    % 100 エポックごとに現在の損失値を表示します。
    if mod(epoch, 100) == 0
        fprintf('Epoch %d, Loss: %.4f\n', epoch, loss);
    end
end

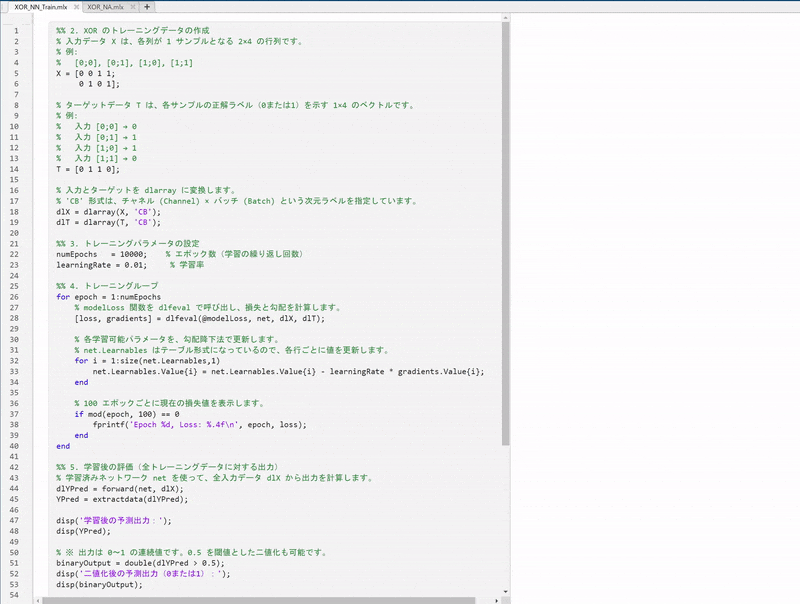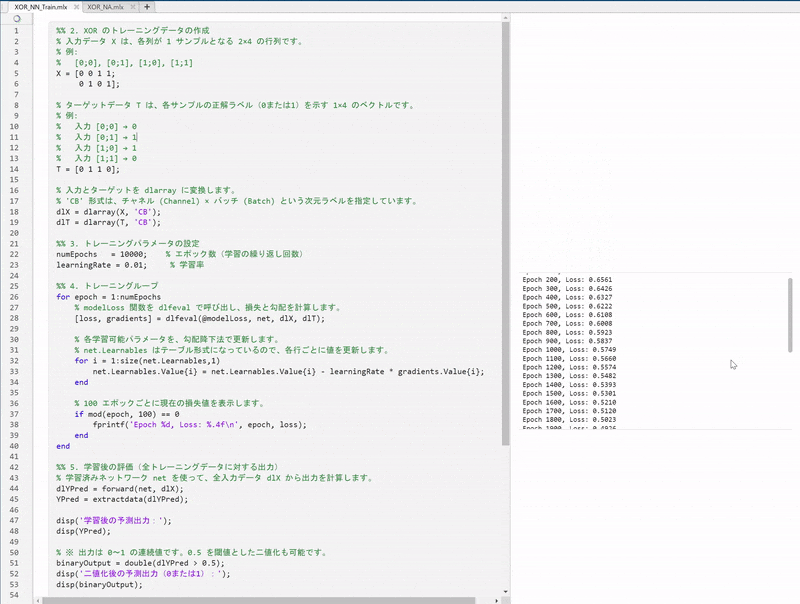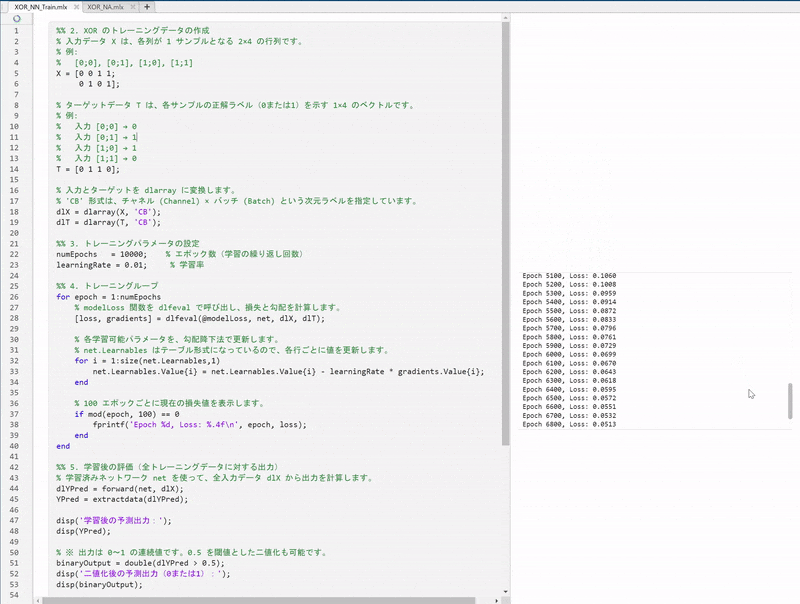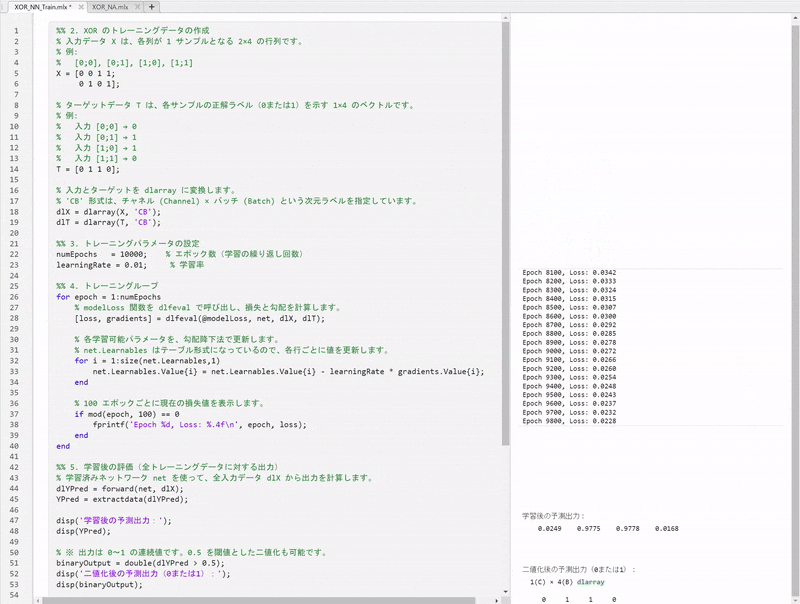
5.4. 学習後の評価

トレーニングが終了した後、学習済みネットワークの性能を評価します。

% 学習済みネットワーク net を使って、全入力データ dlX から出力を計算します。
dlYPred = forward(net, dlX);
YPred = extractdata(dlYPred);

disp('学習後の予測出力：');
disp(YPred);

% ※ 出力は 0～1 の連続値です。0.5 を閾値とした二値化も可能です。
binaryOutput = double(dlYPred > 0.5);
disp('二値化後の予測出力（0または1）：');
disp(binaryOutput);

• 順伝播による予測:
  学習済みのネットワークにトレーニングデータを入力し、出力を計算します。
• 出力の解釈:
  得られる出力は0～1の連続値ですが、一般的には0.5を閾値として、これを基に二値（0または1）に変換し、最終的な分類結果とします。
• 結果の表示:
  連続値および二値化後の出力を表示することで、ネットワークがXOR問題に対して正しく学習できたかを確認します。

5.5. モデルの損失と勾配を計算する関数

modelLoss 関数は、トレーニングループ内で呼び出され、以下の処理を実施します。

function [loss, gradients] = modelLoss(net, dlX, dlT)
    % ネットワークに入力 dlX を与えて順伝播し、出力 dlY を得ます。
    dlY = forward(net, dlX);
    
    % binary cross-entropy 損失を計算します。
    % epsilon は log(0) を防ぐための微小値です。
    epsilon = 1e-8;
    lossElements = - ( dlT .* log(dlY + epsilon) + (1 - dlT) .* log(1 - dlY + epsilon) );
    
    % すべてのサンプルと出力ニューロンに対して平均をとります。
    loss = mean(lossElements, 'all');
    
    % 損失に関して学習可能パラメータの勾配を計算します。
    gradients = dlgradient(loss, net.Learnables);
end

• 順伝播:
  入力データをネットワークに通し、出力を計算します。

• 損失計算:
  binary cross-entropy損失を算出し、予測とターゲットとの差異を数値化します。ここでは、数値計算での安定性を保つために、対数関数の中で0が発生しないように微小な値（epsilon）を追加しています。

• 勾配計算:
  損失に対して、各学習可能パラメータの勾配を求め、これをネットワークのパラメータ更新に利用できるように返します。

この関数は、ネットワークがどの程度正確にXOR問題を解いているかを評価するための指標となり、またパラメータ更新のための勾配情報を提供する重要な役割を担っています。
(XOR_NN_Train.mlx)

補足:
ここまでのコードを実行すると、記事内の図に示された結果が得られるはずです。ただし、ネットワークの構造としては「入力層2、隠れ層3、出力層1」（隠れ層の活性化関数は leakyReLU を採用）としていますが、隠れ層のニューロン数を3個に増やしても、必ずしも局所的最適解に陥らないという保証はありません。
実際の学習結果は、初期重みの設定や最適化アルゴリズム、学習率などのハイパーパラメータに依存します。したがって、シンプルなネットワーク構造であっても、再現性のある学習結果を得るためには、これらのパラメータの調整が重要となります。

6. SimulinkでのNN統合と検証

この章では、MATLABで学習済みのニューラルネットワーク net（ワークスペースに1×1の dlnetwork オブジェクトとして存在）をSimulinkモデルに統合し、その動作を検証する方法を説明します。

6.1. 学習済みネットワークの保存

1. ネットワークの保存:
   MATLABのワークスペースにある学習済みネットワーク net を、右クリックメニューから「保存」を選択して、net.mat といったMATファイルとして保存します。これにより、後でSimulinkモデル内でネットワークを読み込むことが可能になります。

6.2. Simulinkモデルでの統合手順

1. Predictブロックの配置:

   • Simulink上で、Predictブロックを配置し、ブロックのプロパティで先ほど保存した net.mat ファイルを指定します。
   • このブロックは、NNの出力（1である確率）を生成します。
     

2. Compare to Constantブロックの配置:

   • NNの出力は確率値（0～1の連続値）として得られるため、しきい値0.5で二値化するために、Compare to Constant ブロックを配置します。
   • このブロックでは、定数値を0.5に設定し、出力が0.5以上なら1、未満なら0として判定します。

3. 入力信号と出力の確認:

   • 入力信号を供給するため、Constantブロックを用いて、学習時と同様のXORの入力データをSimulinkモデルに与えます。
   • ここで、入力信号の形状がネットワークの仕様に合致するように、Reshapeブロックを用いて信号を 1×2 の形に変換する必要があります。
   • また、シミュレーション中に出力を動的に確認できるよう、スライダーボタンを配置して、パラメータ（例えば入力値など）をリアルタイムに調整できるようにします。
   • Displayブロックを配置し、PredictブロックおよびCompare to Constantブロックの出力を確認します。(XOR_NN.slx)

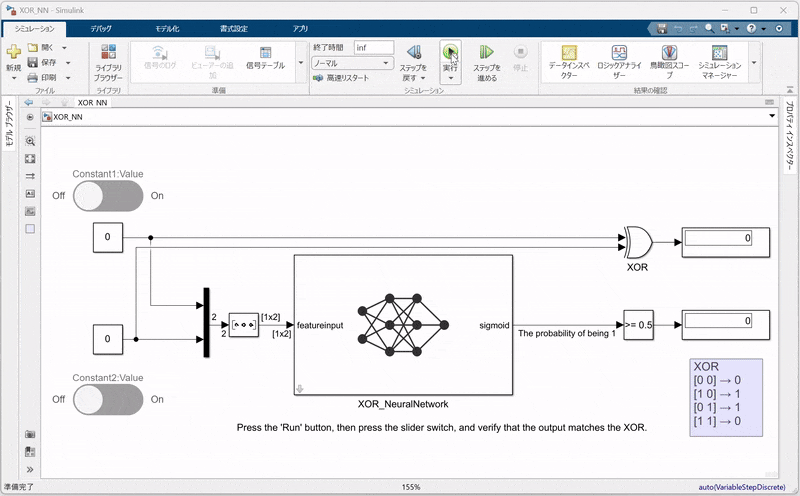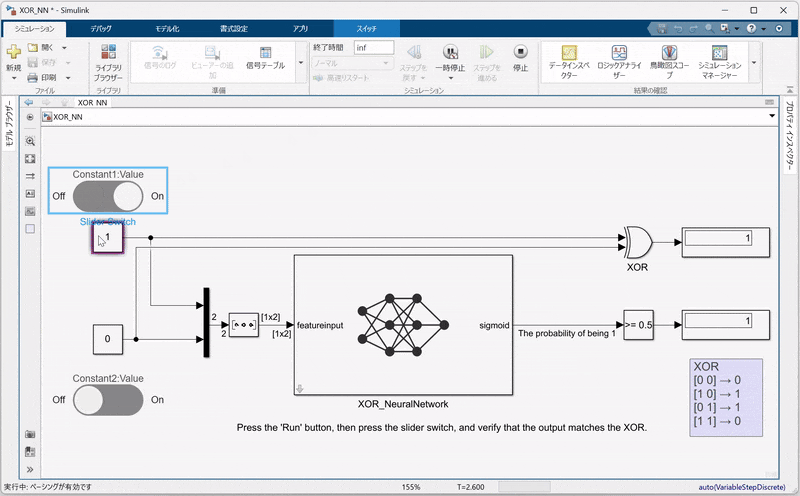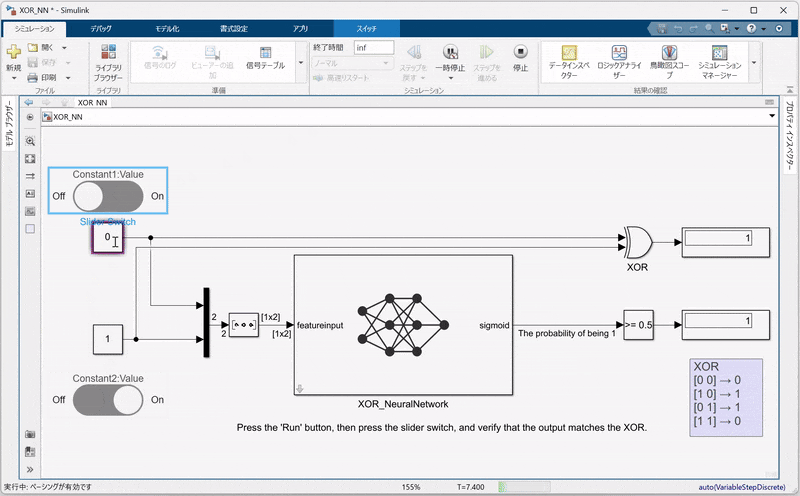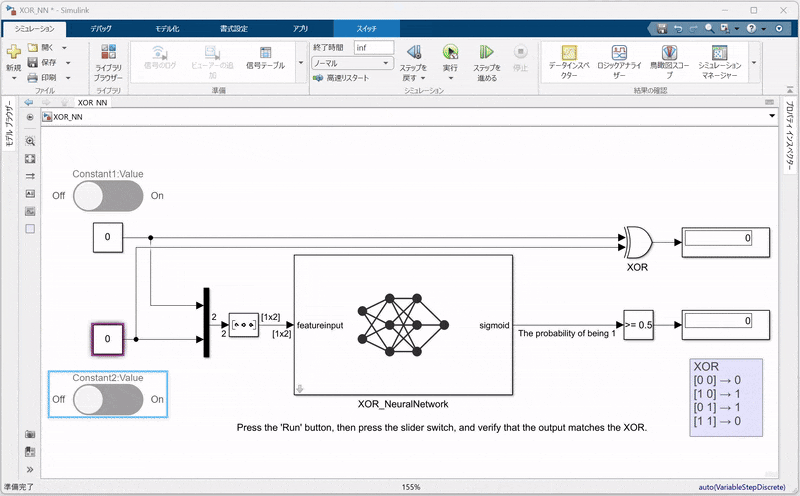
6.3. シミュレーションの実行と結果確認

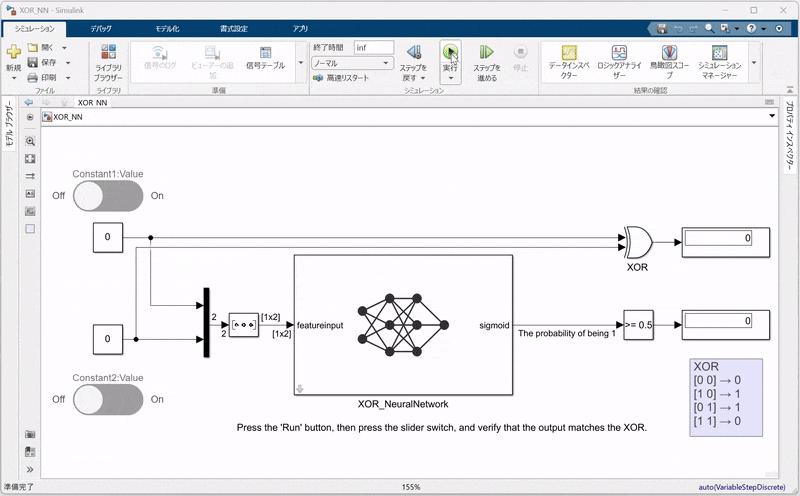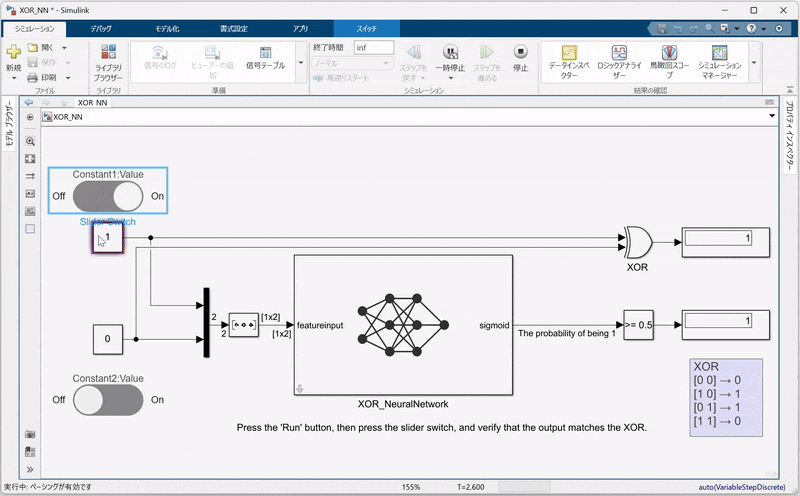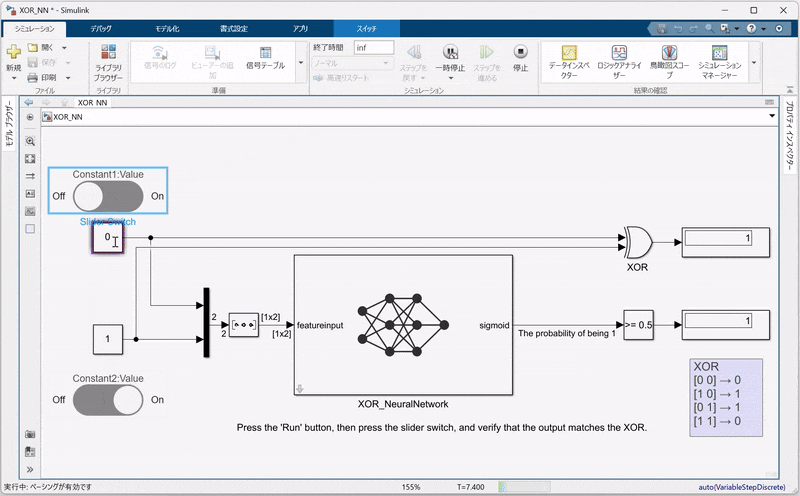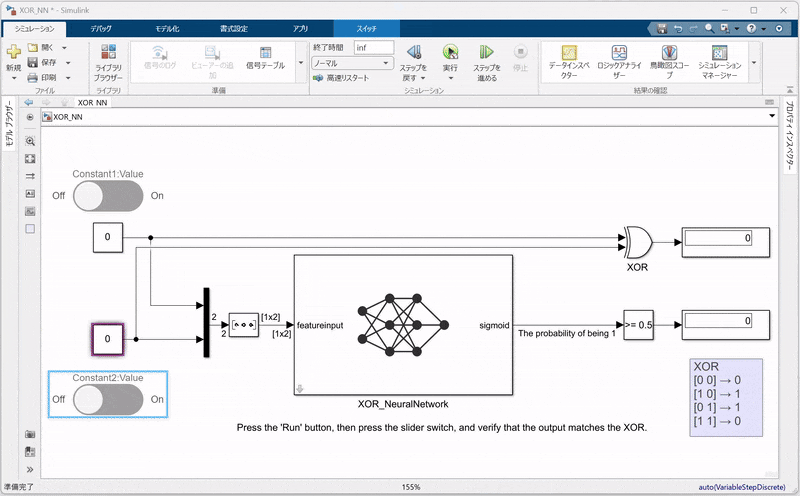
Simulinkモデルが完成したら、シミュレーションを実行してください。シミュレーション結果としては、以下の点を確認できます。

• 二値化された出力:
  Compare to Constantブロックにより、出力が0.5を閾値として二値化され、従来のXOR回路と同じ論理出力が得られていること。

• 動的な入力:
  スライダーボタンを用いることで、シミュレーション中に入力値を調整でき、その変化に応じてNNの出力がリアルタイムで確認できることも確認してください。

この検証により、MATLABでトレーニングした学習済みネットワーク net がSimulinkに正しく統合され、論理回路の動作を再現していることを視覚的に確認できます。

7. まとめ

本記事では、MATLABとSimulinkを用いて、ゼロからシンプルなニューラルネットワークを構築し、XOR問題を解く方法について解説しました。
具体的には、以下のポイントを学びました。

• XOR問題の理解:
  XORの真理値表およびデータ分布を通して、線形分離不可能な問題であることを確認しました。これにより、非線形変換の必要性が理解できました。

• シンプルなNNの構造と理論:
  理論上は入力層2、隠れ層2、出力層1（2層NN）でXORが解けるとされますが、実践では局所最適解に陥りやすいことから、隠れ層のニューロン数を3個に増やし、活性化関数にleakyReLUを使用することで、より柔軟で安定した学習を目指しました。

• MATLABでのNN実装:
  Deep Network Designerやコードを用いて、ネットワークの各層の設定（入力層のInputSize、隠れ層のOutputSize、活性化関数、出力層のシグモイド処理）を具体的に説明しました。

• トレーニングと評価:
  トレーニングデータの作成から、SGDを用いたトレーニングループ、そして学習後のネットワーク出力の二値化まで、実際のコード例とともに学習プロセスを解説しました。

• SimulinkでのNN統合:
  MATLABで学習済みのネットワーク net をMATファイルとして保存し、Simulinkモデルに統合する方法を、図とともに視覚的に説明しました。
  また、入力信号の形状調整（Reshapeブロック）やスライダーボタンによる動的なパラメータ調整を行うことで、シミュレーション中に出力がリアルタイムに確認できる点も紹介しました。

以上の流れを通じて、理論的な背景と実践上の工夫、そしてSimulinkとの連携によるシステム全体の動作確認まで、ゼロからNNを実装してXOR問題を解く一連のプロセスを学ぶことができました。

ここまでのコードやモデルは、以下のGitHubリポジトリにて公開していますので、ぜひ実際にご覧いただき、手元で試してみてください。
https://github.com/Hiroto-Nakano/XOR_Neural_Network