TL;DL
MobileNetsはDepthwise Separable Convolutionを用いることで、通常のCNNと比べて軽いネットワークを構築することがでる。また2つのハイパーパラメータである、width multiplierとresolution multiplierを導入することで、latencyとaccuracyを調節することができる。この技術を用いることで、性能や応答時間に制限があるモバイル上のアプリケーションなどにおいても認識や分類モデルへの応用が可能になる。
MobileNet Architecture
Depthwise Separable Convolution
- depthwise separable convolutions
- depthwise convolution
- pointwise convolution (1×1 convolution)
という構造になっている。
たとえば、112 x 112 x 32という入力に対して、通常のCNNでは、3 x 3 x 32 x 64のカーネルを用いて畳み込みを行い、112 x 112 x 64の出力をする。（図1） 一方で、Depthwise Separable Convolutionでは、まず3 x 3 x (1) x 32のフィルタを用いて、depthwise convolutionを行う。この出力は、112 x 112 x 32のままである。次に、1 x 1 x 32 x 64のフィルタを用いて、pointwise convolutionを行う。この出力が56 x 56 x 64になる。（図2）
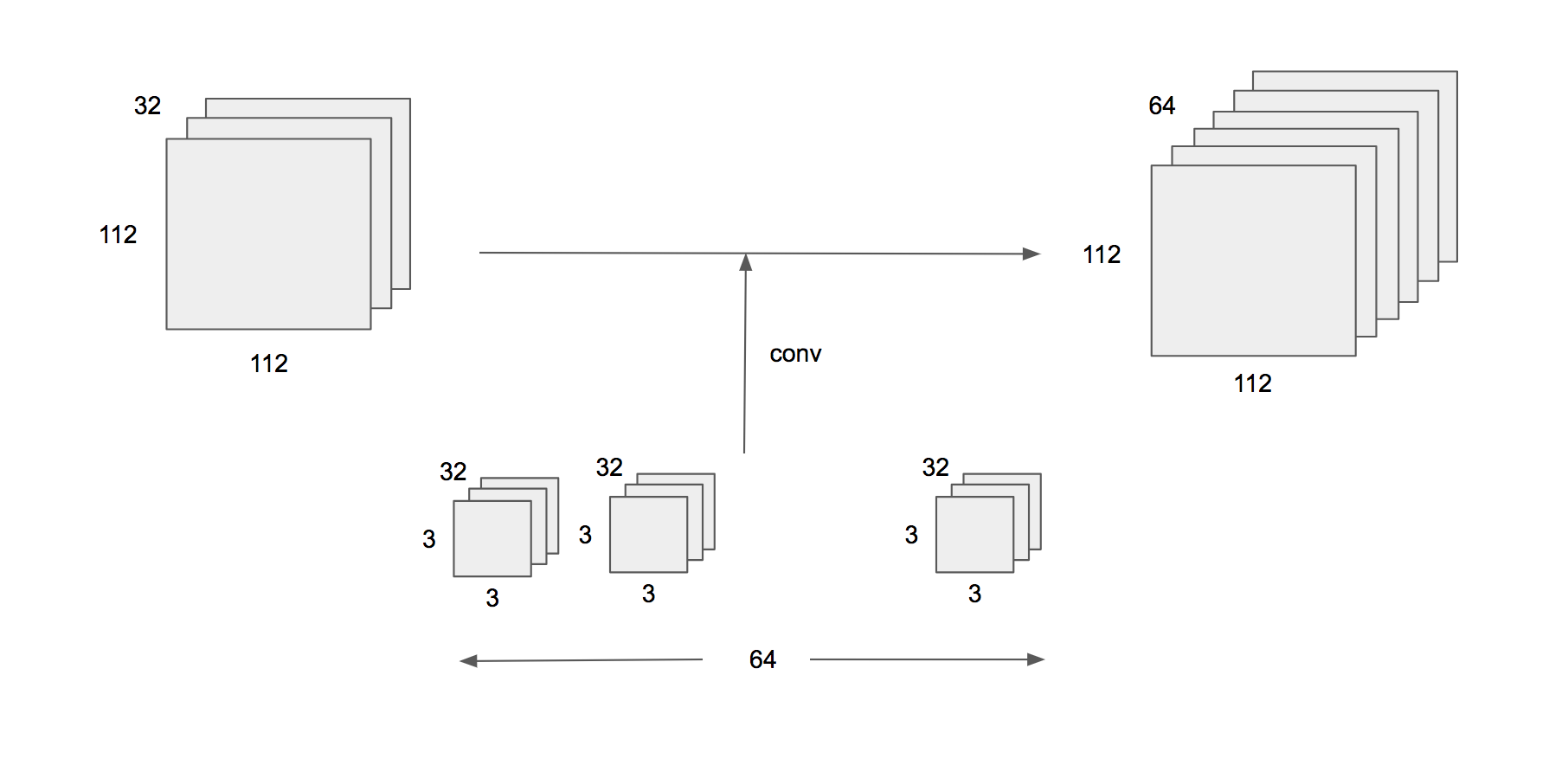図1: 通常の畳み込みイメージ
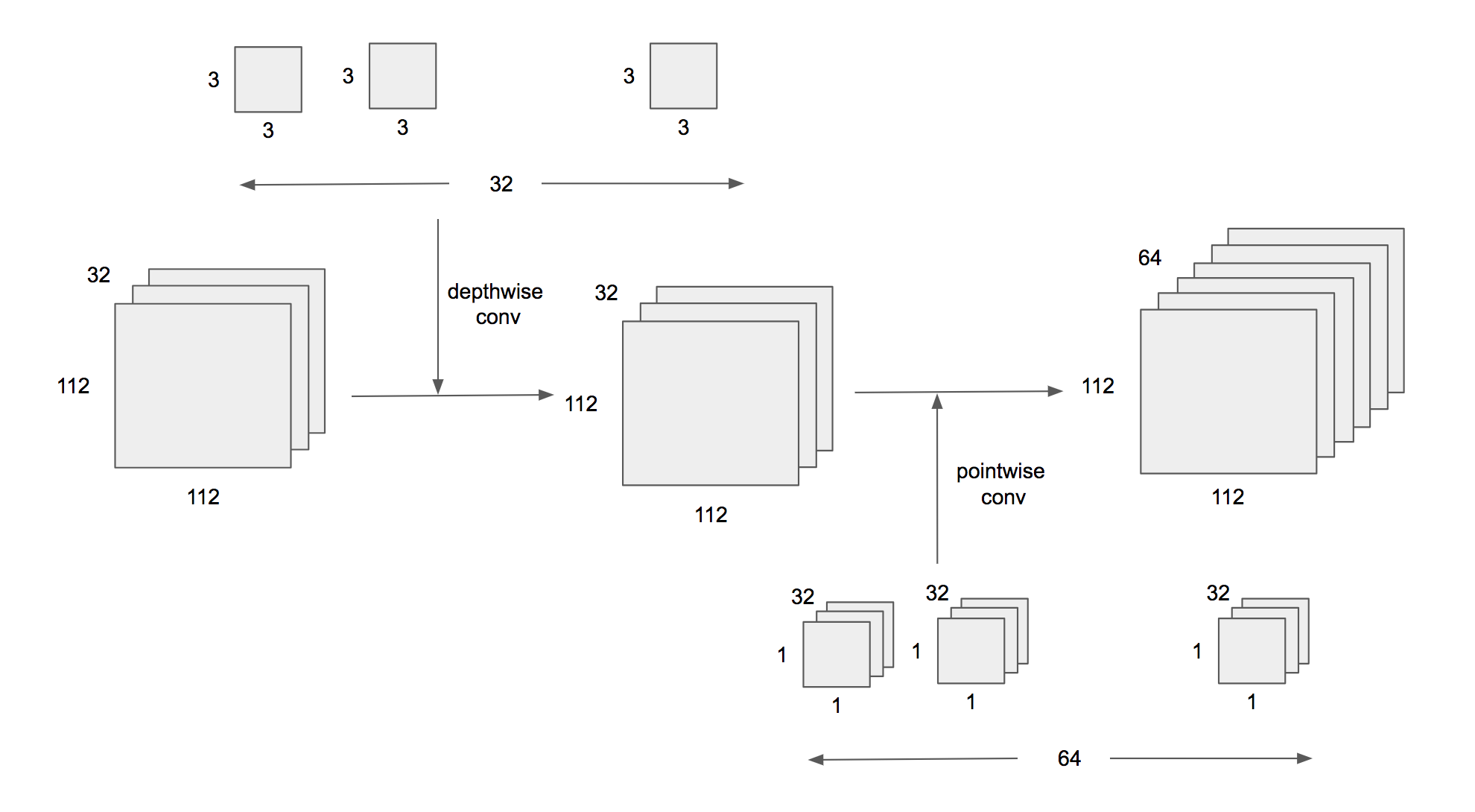図2: depthwise separable convolutionsのイメージ
また、入力の特徴マップサイズを$D_{F} · D_{F} · M$、出力の特徴マップサイズを$D_{F} · D_{F} · N$、カーネルのサイズを$D_{K} · D_{K} · M · N$とすると、通常の畳み込みの計算コストは、
D_{K} · D_{K} · M · N · D_{F} · D_{F} = D_{K}^2MND_{F}^2
である。一方で、depthwise convolutionでは、チャネル方向への畳み込みを行わないため、$M = 1$であり、計算コストは、
D_{K} · D_{K} · N · D_{F} · D_{F} = D_{K}^2ND_{F}^2
また、pointwise convolutionでは、空間方向の畳み込みを行わないため、$D_{K} = 1$であり、計算コストは、
M · N · D_{F} · D_{F} = MND_{F}^2
よって、Depthwise Separable Convolutionでは、計算コストは、
D_{K}^2ND_{F}^2 + MND_{F}^2 = (D_{K}^2 + M)ND_{F}^2
通常の畳み込みに比べて、Depthwise Separable Convolutionは、
\frac{(D_{K}^2 + M)ND_{F}^2}{D_{K}^2MND_{F}^2} = \frac{1}{M} + \frac{1}{D_{K}^2}
だけ、計算コストが削減できている。上の例では、$M = 32$、$D_{K} = 3$であるから、約9倍ほど計算コストが削減されることがわかる。
このようなやり方を取ることで、通常の畳み込みと比べて計算コストとモデルのサイズをかなりの度合いで小さくすることができる。
NNの構造とtraining
MobileNetの構造はTable1に示されている。全ての層がBatch NormalizationとReLUにしたがっており、最後の層は分類のためにSoftmaxが使われている。
Table2でわかるように、MobileNetはその計算のほとんどpointwise convolutionが占めている。
Figure3で、通常のCNN（左）とMobileNet（右）のNNの層の構成が示されている。
Width Multiplier: Thinner Models
上記で示したような、基本のMobileNetの構造でもすでに小さく、latencyも低いが、さらに小さく、速く動作するような構造が要求される場合もある。このような要求に応えるために、width multiplierと呼ばれるパラメータαを導入する。その結果、それぞれの層で、ネットワークを小さく揃えることが可能になる。
例えば、width multiplierであるαを導入すると、入力チャネル数MはαMに、出力チャンネル数NはαNになる。また、αはα ∈ (0, 1]の範囲を取り、一般的には、1, 0.75, 0.5, 0.25が用いられる。
Resolution Multiplier: Reduced Representation
次に、計算コストを削減するためのハイパーパラメータとしてresolution multiplierと呼ばれるパラメータρを導入する。これにより、各層の入力画像とその内部表現を削減することが可能になる。
例えば、resolution multiplierであるρを導入すると、入力画像の大きさDfはρDfに、出力画像の大きさDfはρDfになる。また、ρはρ ∈ (0, 1]の範囲を取る。
以下のTable3では、入力特徴マップサイズ14 × 14 × 512、カーネルサイズ3×3×512×512の時の、通常のCNNと、MobileNet、さらにハイパーパラメータαとρを導入した時の計算量とパラメータ数が比較されている。
Experiments
以下では、MobileNetの性能を様々に比較していく。
Model Choices
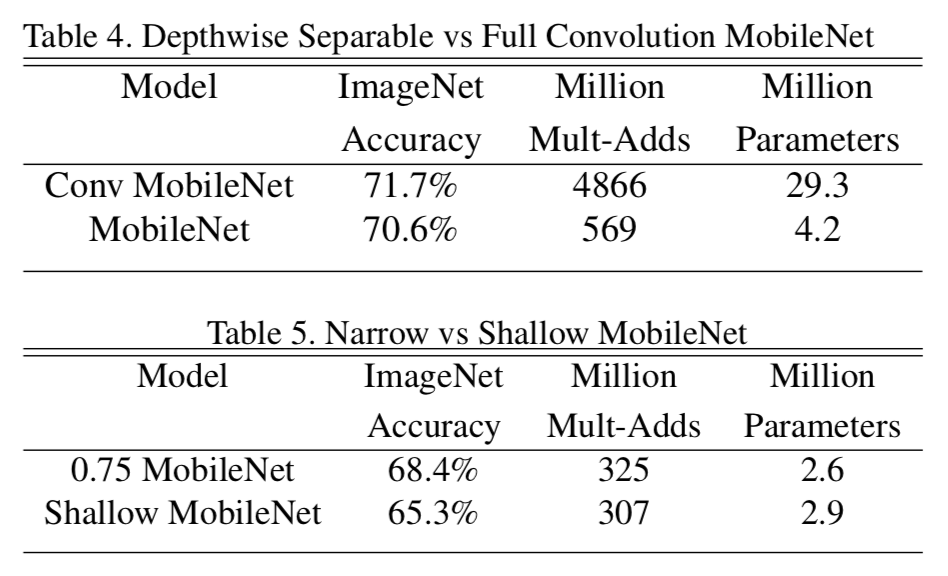
Table4では、全てConvolutionを使ったMobileNetとDepthwise Separable Convolutionを一部使ったMobileNetの性能を比較している。後者は、Multi-AddsもMiParametersも大きく減っているのに対して、Accuracyは1%ほどしか減っていないことがわかる。これにより、Depthwise Separable Convolutionを用いることで、通常の計算コストを大きく抑えながら同程度の精度が出せることがわかる。
またTable5では、width multiplierを導入した場合と、Table1のうちある1つの層を取り除いてShallow（浅くした）構造で比較をしている。どちらも計算コストを抑えるが、精度は3%ほど前者の方が高くなっている。
Model Shrinking Hyperparameters
Table6では、width multiplier αによる、精度と計算コストのトレードオフの関係が示されている。αを小さくすればするほど、計算コストは抑えられるが、その分精度は下がっている。
またTable7では、resolution multiplier ρによる精度と計算コストのトレードオフの関係が示されている。これもwidth multiplierと同様に、ρを小さくすればするほど、計算コストは抑えられるが、その分精度は下がっている。
Figure5では、width multiplier α ∈ {1, 0.75, 0.5, 0.25}とresolutions {224, 192, 160, 128}とハイパーパラメータを設定した時の精度と計算コストの関係を示している。
