[機械学習]初心者に向けてアヤメ分類を一から解説してみた #Python

こんにちは。ひろちです。

機械学習を始めたばかりという初心者に向けて、アヤメ分類を解説いたします！
詳しく説明を加えながら書いたので、是非参考にしてみてください！

↓記事を読む前に筆者について知りたい方へ↓
>>>詳しいプロフィールはコチラ

～目次です～
1. 対象読者とか書いてみる
 2. 《Google colaboratory》で進めていきます
 3. 色々とimportしていく
　　・オートパイロット状態でimportする奴ら
　　・scikit-learnの様々な機能をimport!!
4. アヤメのデータセットをじっくり見ていく
　　・インスタンスを生成
　　・アヤメデータはどうなってるの？
5. Pandasを用いてデータを分かりやすくする
　　・配列をDataFrameに変換しよう！
　　・実際にDataFrameを見ていこう！
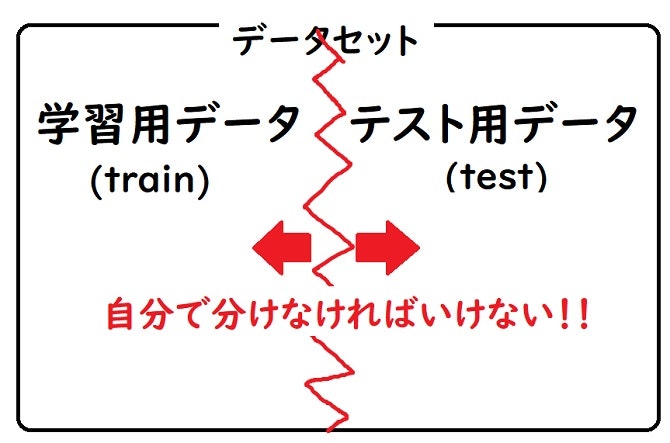
6. データセットを分割する
　　・説明変数と目的変数とは？
　　・学習用とテスト用のデータはどうするの？
　　・train_test_split関数を使う！
7. データをmatplotlibで可視化する
　　・データを可視化する意味は？《特徴量選択》
　　・散布図をplt.scatterで描いていく！
8. 機械学習アルゴリズムを使っていこう！
　　・特徴量を選択しよう！
　　・モデルを構築⇒学習⇒予測させる
　　・モデルが予想したデータの答え合わせ
　　・2つの結果の違いについて詳しく見る

1. 対象読者とか書いてみる

今回は機械学習でアヤメの分類を行っていくことが主題なので、レベルとしてはこんな感じ。

何かしらのNotebook形式でプログラムを実行できる人
Python初心者以上
機械学習の流れが何となくわかる人

2. Google Colaboratoryで進めていきます

今回はバージョンとか、仮想環境とか…諸々のしがらみに囚われたくなかったので、Google Colaboratoryにてアヤメ分類をしていきたいと思います。

始め方はすごく簡単で、Google Colaboratoryのサイト左上の《ファイル》から《Python3の新しいノートブック》をクリックしてください。

すると新しいノートブックが生成されるので、左上のUntitled0.ipynbから名前を変更してあげてください！

※僕は名前を『初めてのアヤメ分類』にしておきました。笑

初学者の方はページを見つつ、一から作成することをオススメしますが、一応完成形も↓のGitHubにてノートブックを公開しています。
>>>GitHubへはコチラから

3. 色々importしていく

オートパイロット状態でimportする奴ら

とりあえず以下をインポートしていきますね。(矢印先は僕のライブラリへの感想です。)

Numpy　⇒　計算機能凄めライブラリ
Pandas　⇒　表を扱いやすいライブラリ
Matplotlib　⇒　グラフ可視化ライブラリ
warnings　⇒　~~たまに邪魔な~~警告を消すライブラリ

そしてプログラム化するとこんな感じ。

importするライブラリ.ipynb

import numpy as np
import pandas as pd
import matplotlib
import matplotlib.pyplot as plt
%matplotlib inline
import warnings
warnings.filterwarnings('ignore')

scikit-learnの色々な機能をimport!!

機械学習ライブラリのscikit-learnには分類を行う以外にも様々な機能が存在しています。今回使用するものをサラっと紹介しますね。(後で深堀りしていきます)

1つ目はscikit-learnに用意されているデータセットです。
scikit-learnのデータセット集一つにアヤメのデータセットがあります。
>>>詳しくはコチラ(UCI Machine Learning Repository: Iris Data Set)

２つ目が学習用とテスト用にデータセットを分ける機能です。
分ける理由としては、《学習用のデータで予測するモデルを作成する》⇒《テスト用データで作成したモデルは良い物か判定する》という機械学習では鉄板の2つの処理を行いたいからです。

3つ目が分類を行うアルゴリズムになります。機械学習には様々な分類のアルゴリズムが存在して、以下のプログラムではアルゴリズムとして『線形のSVM』を用いるので、LinearSVCをインポートしています。
>>>SVM(サポートベクターマシーン)について詳しく知りたい方はコチラ(Qiita)

では上記で紹介した3つをimportしていきます。

scikit-learnの様々な機能をimport.ipynb

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.svm import LinearSVC

4. アヤメのデータセットをじっくり見ていく

まず今回の目的をハッキリさせておきましょう！

どのサイトでも分類の部分を重要視しすぎて、結局何がしたかったのか見失いがちです。

今回の目的は…

『アヤメのがく片や花びら幅や長さの数値』を用いて『アヤメ属(花)の種類を分類する』こと

そこで既にアヤメの種類によっての幅や長さのデータを数値を集めてくれているデータセット(先ほどimportした奴)を使って、機械学習により予測していきます。

フィッシャーのアヤメのデータから散布図行列を描く(https://teenaka.at.webry.info/201803/article_12.html )から引用

ちなみに上の図がアヤメになります。この花の長さや幅を測定して数値化したデータセットをimportしました(/・ω・)/

インスタンスを生成

今はアヤメのデータセット機能をインポートしただけなので、まずインスタンスを生成していきます。

アヤメインスタンスを生成する.ipynb

heacet = load_iris()

インスタンスの名前に特に深い意味はないです。単に自サイトの宣伝をしているだけです！笑

もし嫌だという方はコピーするだけではなく、自分で書いていくと理解も深くなるので、ここのインスタンス名を変えて実行してみてください！

アヤメデータはどうなってるの？

さっそくデータセットの中身を見ていきましょう。
↓コチラを実行してください↓

アヤメデータの中身を確認する.ipynb

print("与えられたデータ")
print(heacet.data)
print(heacet.data.shape)
print("-----------------")
print("予測するデータ")
print(heacet.target)
print(heacet.target.shape)
print(heacet.target_names)

実行して出力を見ると、どうやら《数値が書かれた150×4の2次元配列》と《0,1,2と書かれた150×1の1次元配列》が得られたみたいですね。

また0,1,2はそれぞれ『setosa』,『versicolor』,『virginica』対応していることも分かります。

よって与えられた《数値が書かれた150×4の2次元配列》を《データセットを学習用と予想用に振り分け》て、《どれが0,1,2に対応するのか》を《機械学習アルゴリズム》に通して、《予想して》いく流れが見えてきます。

さて、これらのデータをpandasを用いて見やすくしていきましょう(/・ω・)/

5. Pandasを用いてデータを分かりやすくしよう！

今のままでは配列が出力されただけで、何のデータなのかよくわからない状況になっています。

そんな時に表を列ごとに名前を付けて見やすくできたり、平均値や標準偏差などを自動で出してくれるというPandasライブラリを使っていきます。

配列をDataFrameに変換しよう！

今からやっていくことはこんな感じ↓

DataFrameの第一引数にデータセット、第二引数にカラムの名前を与える。
DataFrameの第一引数に目的変数、第二引数にカラムの名前を与える。
1と2のDataFrameを横に結合したDataFrameを作る

↓なのでプログラムはこんな感じになります↓

Pandasの定義する.ipynb

heacet_data = pd.DataFrame(heacet.data, columns=["がく片の長さ","がく片の幅","花びらの長さ","花びらの幅"])
heacet_target = pd.DataFrame(heacet.target, columns=["花の種類"])
heacet_all = pd.concat([heacet_data,heacet_target], axis=1)

恐らく1行目と2行目のプログラムは大体何をしているか分かると思いますが、3行目に『concatメソッド』を用いて、引数に『1行目のデータと2行目のデータを選択』して、『axis=1』と定義しています。

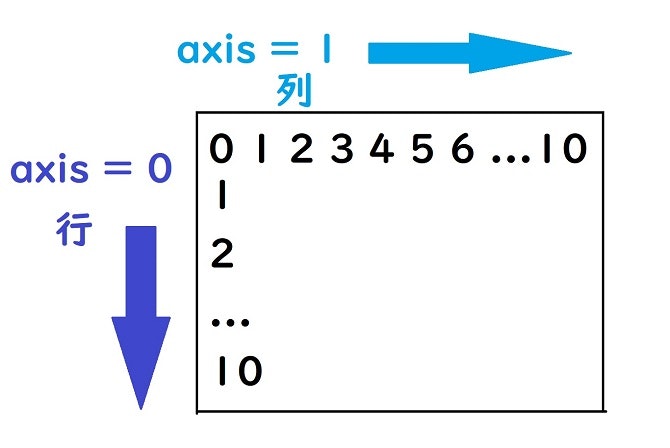
axis=1ってなに？？

『axis』は恐らくよく見かけているのではないでしょうか。今後も使っていくと思うので、しっかりと確認しておきましょう！

【　axisとは軸を指定する引数　】

図で簡単に表すとこんな感じ↓

axis=0だと縦の行を示して、axis=1だと横の列を示していることになります。

そこで今回は、DataFrameであるheacet_dataのcolumnsに《花の種類》というcolumnを横に追加したかったので、axis=1と指定したわけですね。

実際にDataFrameを見ていこう!

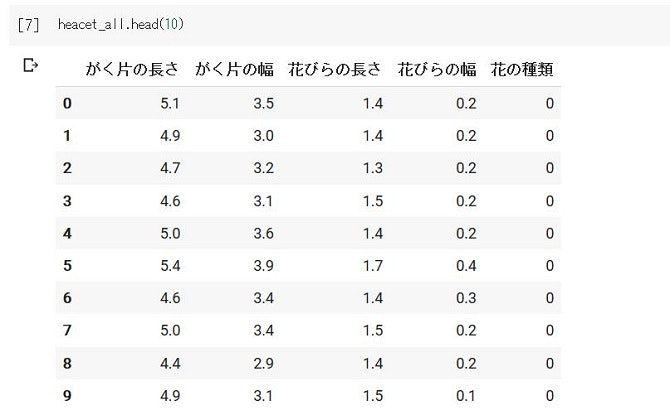
さてさて、PandasのDataFrameを使ったことで見やすくなったはずなので、見にいきましょう～

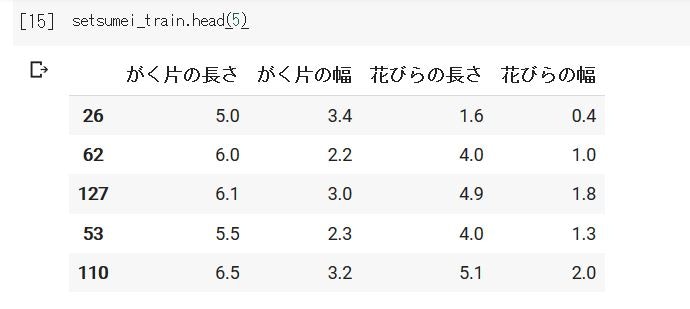
headメソッドを使って最初の10行を見てみます。

とてもまとまっていて、2次元配列を単に出力した時とは見やすさが大違いですね。笑

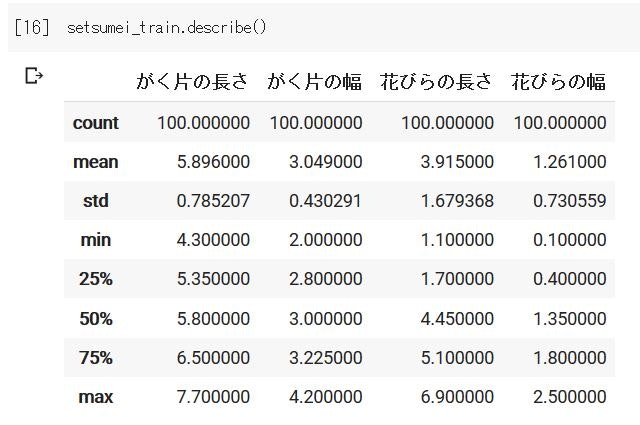
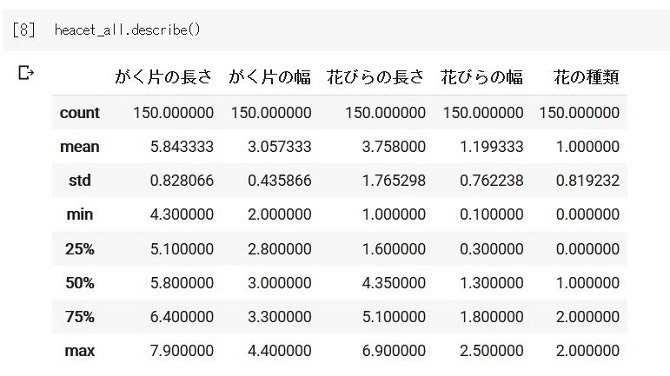
またPandasでは平均値などを出してくれるdescribeメソッドもあるので、是非実行してみてください！

6. データセットを分割する

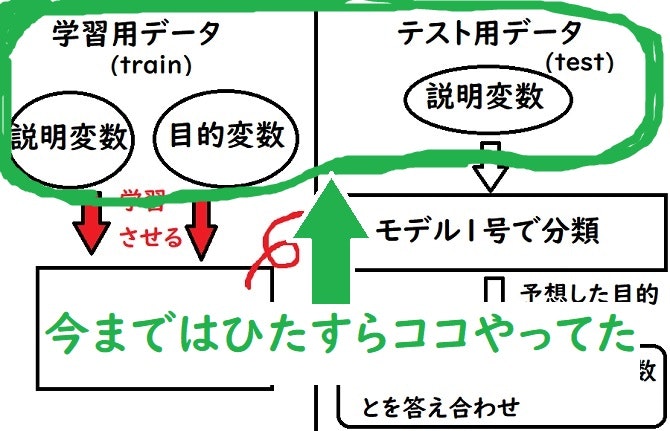
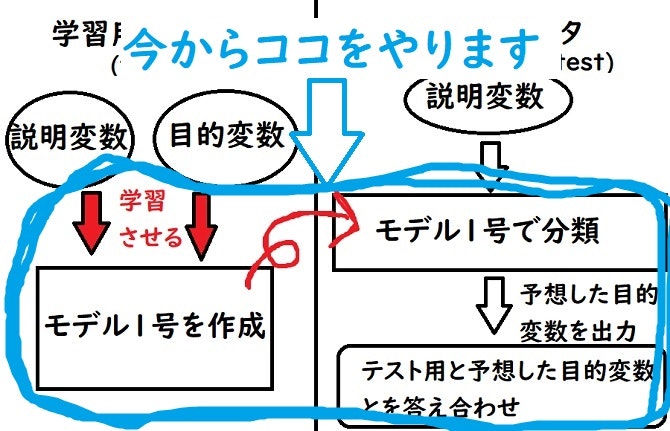
そもそも論なんですが、予測するデータはすでに答えが存在してしまっているので、自分で学習させるデータと予測するデータを創り出さなければなりません。

冒頭で訓練用とテスト用に分ける機能をインポートしましたよね。やっとここで使います。
ですが少し待ってください。ある用語を説明していなかったので、ここで挟みます。

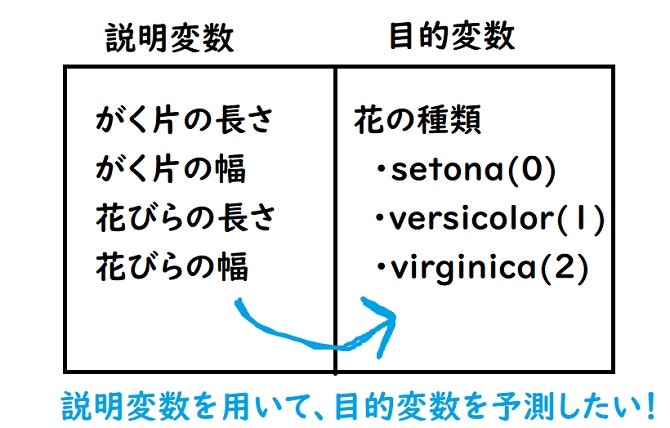
説明変数と目的変数とは？

ゴリゴリペイントで書いた感のある図で説明していきます！

上の図のように今まで《がく片の長さ、がく片の幅、花びらの長さ、花びらの幅》といったカラムを付けていた部分を説明変数、《花びらの種類》とカラムを付けていた部分を目的変数と呼びます。
これから多用していくので、是非覚えておいてください！！

そして単純に説明変数と目的変数を使って学習をさせていきたいのですが、まだ学習用とテスト用のデータを分割していませんでした！

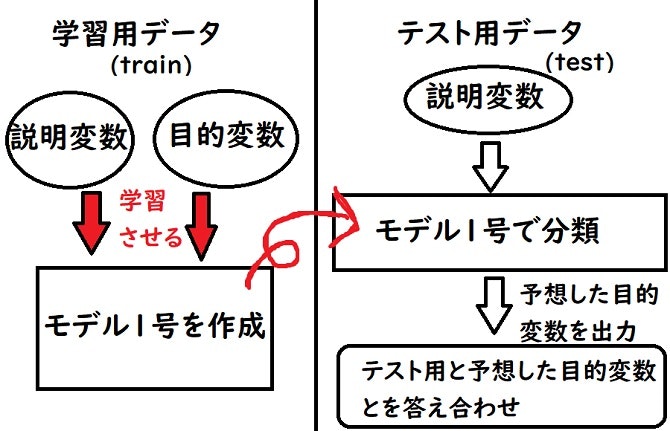
え、そもそも学習用とテスト用のデータってなに？

↑上図のように学習用データを使って学習させてモデルを作成して、テスト用データを使ってモデルが正確に動作しているか確かめるという流れが機械学習にはあります。

この一連の流れをこなす為に《学習用データ》と《テスト用データ》が必要となってきます。

実はこの『学習用とテスト用(詳しくはvalidation用)のデータを分ける』という段階は深堀りすれば、Kaggler達で様々な議論が行われているような分野みたいです…

この記事はそんな話題には触れず、サラッと進めていきます。笑

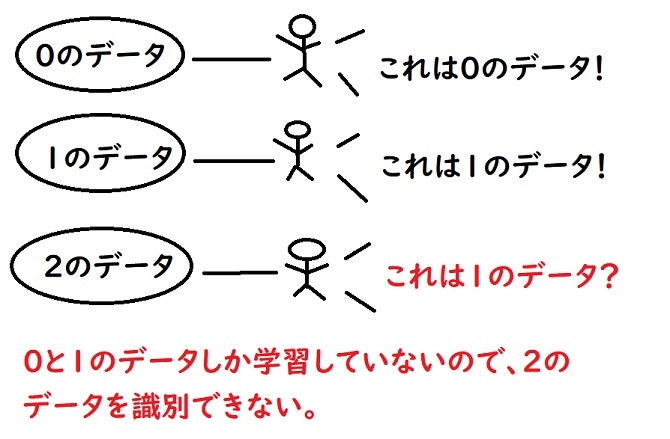
てか『データなんてPythonでシンプルに分ければ良いじゃないか！』という話なのですが、先ほどの《花の種類》の目的変数を見て頂けたら分かる通り、0⇒1⇒2の順番で目的変数が並んでいます。

ここでもしスライスを使ってデータを半分に分けたりすると、上部分の目的変数が0と1のデータしかモデルは識別できないので、目的変数が2であるデータに対して有効的なモデルを作ることができません。

ペイント間満載の図を使っていくと…

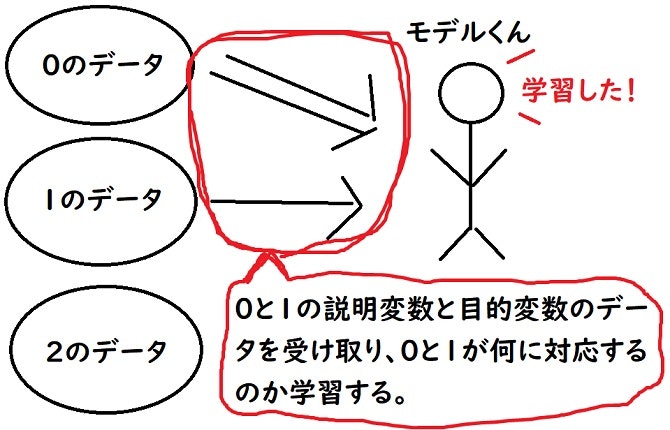
↑上では『0のデータ』と『1のデータ』しか学習していません。

↓結果的にこのような事が起こります。

図にしてしまえば単純な話ですね！

そこで、
『データを学習用とテスト用に分ける且つシャッフルしてくれるような機能があれば良いなぁ～』
なんて思う訳です。

『あります。train_test_split関数があります！！！』

散々言葉の定義について書いてきましたが、やっとプログラムを書いていきます。笑
ここで冒頭にてimportしたtrain_test_split関数を使います。

train_test_split関数を使う

今回は学習用の説明変数と目的変数、テスト用の説明変数と目的変数を以下のように定義します。

学習用の説明変数　⇒　setsumei_train
学習用の目的変数　⇒　mokuteki_train
テスト用の説明変数　⇒　setsumei_test
テスト用の目的変数　⇒　mokuteki_test

これらをプログラム化するとこうです↓

学習用とテスト用の説明変数と目的変数を定義する.ipynb

setsumei_train,setsumei_test,mokuteki_train,mokuteki_test = train_test_split(heacet_data, heacet_target, test_size=0.33)

引数としてtest_sizeというものがあります。これはデータセットをどれだけテスト用に使うかを割合で設定する引数です。

今回は『データセット50個分 = 全体の1/3 = 0.33』をテスト用に使うので、引数を『0.33』としています。

しっかりと分けれているか見ていきます。僕はこうなりました↓

良い感じにシャッフルされて、100個50個で分かれていますね。またID番号も同じなので良い感じです( *´艸｀)

7. データをmatplotlibで可視化する

次は効果的な特徴量を見つけるために、matplotlibでデータを可視化していきます。

データを可視化する意味は？《特徴量選択》

特徴量とは説明変数のことを指していて、『特徴量　≠　説明変数』であることは覚えておいて欲しいのですが、今は同じものとしておきます。

さてデータを可視化することで、効果的な特徴量選択が行えるということを例えを出して説明していきます。

ここでまず一つ心に置いてほしいことが、今回用いる機械学習の分類のモデル(SVM)はざっくり言うと、それぞれのアヤメデータ(がく片や花びらの長さや幅)をプロットして、その距離が最も離れている線を学習を行った後に、本番でその学習した線の分け目によってアヤメの種類を見分ける方法を取ります。

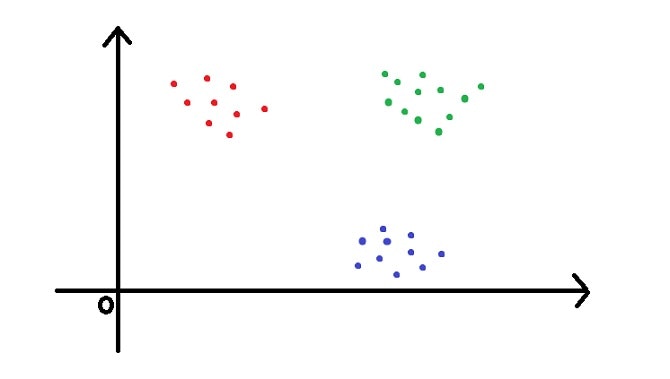
ではまず例題として、グラフ上にプロットしている赤と緑と青の点についてそれぞれで分類したいとします。

このとき↓下の２つの図ではSVMを用いた時、どちらの方が正しく分類できるでしょうか？

↑これが1つ目の図

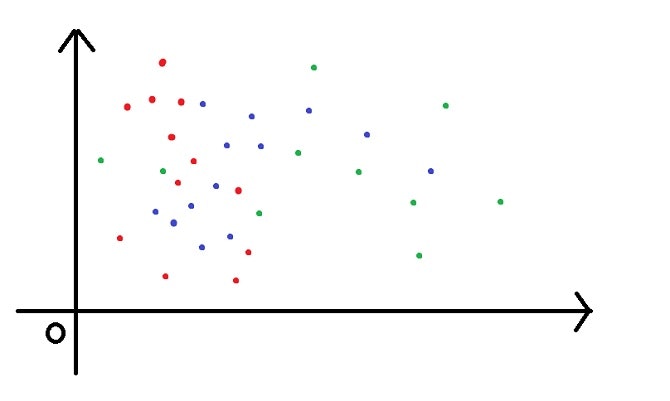
↑これが2つ目の図

ぱっと見2つ目の図のほうが正しく分類できそうですね〜。

SVMにおいてこれは正解です。なぜなら分類したい点と点との距離が離れれば離れるほどSVMの精度は良くなってきます。

少し極端な例でしたが、上下の図のように選択する特徴量によって、分類のしやすさが変化することがあります。

今回のアヤメの分類で言えば、《がく片の長さ》《がく片の幅》《花びらの長さ》《花びらの幅》で2つ特徴量を選ぶとすれば、組み合わせによって分類のしやすさが変わってくるということです。

散布図をplt.scatterで描いていく！

matplotlibのscatterメソッドは引数として以下を指定します。

横軸にしたいデータ
縦軸にしたいデータ
label=凡例
cmap=カラーマップの種類

カラーマップを用いて色分けしていくのですが、様々な色分けの方法が存在します。
>>>指定できるカラーマップの一覧はコチラ(matplotlib公式リファレンス)

早速matplotlibを使ったプログラムを書いていきたいのですが、花の種類によって視覚的に分類の正確さを測るために目的変数別に色を変えていきます。

目的変数をフィルタリングする方法が僕は少し躓きました。詳しい方がいたらコメントを頂けたら嬉しいですm(__)m

縦軸と横軸データの選択時に上下どちらの引数を使っても大丈夫だったので、実際に左右で使っています。

setsumei_train[(mokuteki_train == 0).values]["がく片の長さ"]
setsumei_train[mokuteki_train["花の種類"] == 0]["がく片の長さ"]

がく片の長さと幅を使って、プロットしていきます。

pltでプロットする(がく片).ipynb

plt.scatter(setsumei_train[mokuteki_train["花の種類"]==0]["がく片の長さ"],setsumei_train[(mokuteki_train == 0).values]["がく片の幅"],label="setosa",cmap="rgb")
plt.scatter(setsumei_train[mokuteki_train["花の種類"]==1]["がく片の長さ"],setsumei_train[(mokuteki_train == 1).values]["がく片の幅"],label="versicolor",cmap="rgb")
plt.scatter(setsumei_train[mokuteki_train["花の種類"]==2]["がく片の長さ"],setsumei_train[(mokuteki_train == 2).values]["がく片の幅"],label="virginica",cmap="rgb")

## X軸の範囲を指定
plt.xlim(3,9)
## Y軸の範囲を指定
plt.ylim(1,5)

## X軸の名前
plt.xlabel("Length of sepal")
## Y軸の名前
plt.ylabel("Width of sepal")

## グラフのタイトル
plt.title("Relation between length and width of sepal")
## 凡例を出力
plt.legend()

先ほど上下どちらでも良いと言いましたが、目的変数をフィルタリングする方法が一つは『Numpyで2次元でブールインデックス参照をしている？』のと、『Seriesのブール値をDataFrameに入れることによって、フィルタリングしている？』方法があります。
この考えが正しいのか証明できる文献がイマイチ探せなかったので、詳しい方がいたらコメントを頂けたら嬉しいですm(__)m

一応その結果は残しておきます。

zikken.py

>>> mokuteki_train == 0
## ブール値でDataFrameが返ってくる
>>> mokuteki_train["花の種類"] == 0
## ブール値でSeriesが返ってくる
>>> (mokuteki_train == 0).values
## np行列でブール値の2次元配列が返ってくる
>>> (mokuteki_train["花の種類"] == 0).values
## np行列でブール値の1次元配列が返ってくる

# この時setsumei_train[mokuteki_train["花の種類"]==0]と
# setsumei_train[(mokuteki_train == 0).values]が全く同じ値を返します。

また花びらの長さと幅でプロットする例も示しておきます。

pltでプロットする(花びら).ipynb

plt.scatter(setsumei_train[mokuteki_train["花の種類"]==0]["花びらの長さ"],setsumei_train[(mokuteki_train == 0).values]["花びらの幅"],label="setosa",cmap="rgb")
plt.scatter(setsumei_train[mokuteki_train["花の種類"]==1]["花びらの長さ"],setsumei_train[(mokuteki_train == 1).values]["花びらの幅"],label="versicolor",cmap="rgb")
plt.scatter(setsumei_train[mokuteki_train["花の種類"]==2]["花びらの長さ"],setsumei_train[(mokuteki_train == 2).values]["花びらの幅"],label="virginica",cmap="rgb")

plt.xlim(0,8)
plt.ylim(0,4)

plt.xlabel("Length of petal")
plt.ylabel("Width of petal")

plt.title("Relation between length and width of petal")
plt.legend()

そして↓下図ががく片の長さと幅を使ってプロットした結果

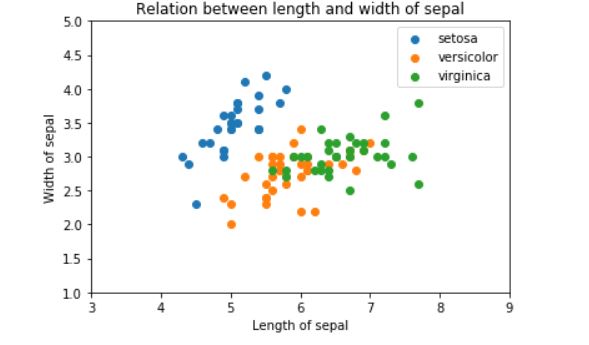これは分類しにくそうですね。人間である僕からしても、どこに区別する線を引いたら良いのかわかりません。笑

そして↓下図が花びらの長さと幅を使ってプロットした結果

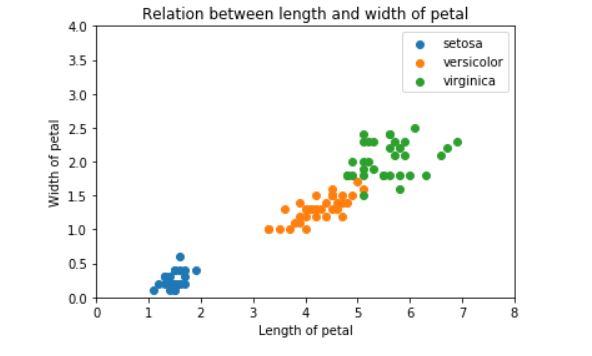
これはそれぞれ目的変数の集合ができているので、簡単に分類する境界線が引けそうですね！
このように選択する特徴量によって、分類のしやすさが変わってくることが視覚的に分かりました。

8. 機械学習アルゴリズムを使っていこう！

ついに機械学習のアルゴリズムに触れることができます。

といってもLinearSVCを用いることを決めてしまっているので、もうそこまでやることはないです。

『ハイパーパラメータを決める』といった段階もありますが、今回は『機械学習の一連の流れをつかむ』ことを重きに置いているので触れないでおきます。気になる方は下のリンクで参考文献を貼っておきます。
>>>LinearSVCのハイパーパラメータの詳しい説明はコチラ

特徴量を選択しよう!

では先ほどMatplotlibを使って可視化させた2つのパターン(がく片コンビと花びらコンビ)の特徴量を選択していきます。
新たに2つのDataFrameとして定義すると、《名前による参照メソッドloc》を使って、プログラムは以下になる。

2つの特徴量を作成する.ipynb

## がく片コンビのDataFrameを作成する。
gakuhen_train = setsumei_train.loc[:,["がく片の長さ","がく片の幅"]]

## 花びらコンビのDataFrameを作成する。
hanabira_train = setsumei_train.loc[:,["花びらの長さ","花びらの幅"]]

LinearSVCでモデルを構築⇒学習⇒予測させる

やっとモデル構築までたどり着きました。笑

もう一度ここ付近の話を説明した図を引っ張ってきますと、

今までは『与えられたデータセットがどうなっているか見たり』、『学習用とテスト用でデータを分けたり』と上図での上の方をずっとやっていました。

ですがこれが『機械学習という分野の一種の特徴』だそうで、機械学習は『前処理に時間がとられる』と聞いたことありませんか？？

まさにそれを具現化しちゃいましたね。記事の大半を占めてしまっています。

そして次にやる機械学習アルゴリズムを実装させる部分は『機械学習アルゴリズムを理解するのは難しい』けれど、『実装させるのは超簡単』という分野で、すぐに終わります。

よって冒頭で定義したLinearSVCを使っていきます。プログラムはこんな感じ↓

LinearSVCでモデル構築⇒学習⇒予測する.ipynb

## それぞれモデルを構築
## それぞれモデルを構築
gakuhen_model = LinearSVC()
hanabira_model = LinearSVC()

## それぞれのモデルに学習させる
gakuhen_model.fit(gakuhen_train,mokuteki_train)
hanabira_model.fit(hanabira_train,mokuteki_train)

## それぞれのモデルで予測させて、予測値を代入させる
### モデルが《がく片の長さと幅》を使って学習しているので、予測する時も《がく片の長さと幅》を渡す必要がある。
gakuhen_predict = gakuhen_model.predict(setsumei_test.loc[:,["がく片の長さ","がく片の幅"]])
### モデルが《花びらの長さと幅》を使って学習しているので、予測する時も《花びらの長さと幅》を渡す必要がある。
hanabira_predict = hanabira_model.predict(setsumei_test.loc[:,["花びらの長さ","花びらの幅"]])

ついに答え合わせです！ここで上で立てた仮説を検証できますね。

Matplotlibで可視化させた図では『《がく片の幅と長さ》は正確に分類できなさそう』でした！
>>>がく片の長さと幅を可視化したグラフはコチラ

逆に『《花びらの幅と長さ》は《がく片の幅と長さ》よりかは正確に分類できそう』でしたね！
>>>花びらの長さと幅を可視化したグラフはコチラ

モデルが予想したデータの答え合わせ

では答え合わせできるプログラムをインポートして、実行していきます。

accuracy_scoreを使う.ipynb

## sklearnライブラリからscore算出の関数をimport
from sklearn.metrics import accuracy_score

## gakuhen_scoreとhanabira_scoreにそれぞれに結果を代入
gakuhen_score = accuracy_score(mokuteki_test, gakuhen_predict)
hanabira_score = accuracy_score(mokuteki_test, hanabira_predict)

print('がく片の長さと幅コンビの正解率：{}'.format(gakuhen_score),'花びらの長さと幅コンビの正解率：{}'.format(hanabira_score), sep='\n')

↓僕は出力結果として以下が得られました！↓

とりあえずどちらも正答率が8割を超えているので、機械学習によってアヤメの種類を分類することはひとまず成功しましたね！

ではでは…

結果について考察していきます。

2つの結果の違いについて詳しく見る

人間の目で見ても《がく片の長さと幅》より《花びらの長さと幅》の方が正確に分類しやすそうでしたが、LinearSVCアルゴリズムにとっても同じように《花びらの長さと幅》の方が正確に分類できるようです。笑

ですが『LinearSVCアルゴリズムにとっても同じように《花びらの長さと幅》の方が正確に分類できる』というのは僕の推論でしかないのです。

実際に確かめるには、どこで境界を作っているのかをMatplotlibを使って可視化していくと良いですよね！！

《がく片の長さと幅》と《花びらの長さと幅》でそれぞれ境界線を見たいので、代入できる関数として定義していきます。

分類の境界を可視化する.ipynb

def heacet_border_check(H, M, model, param1, param2, resolution=0.01):
    H1_min, H1_max = H[param1].min()-0.5, H[param1].max()+0.5
    H2_min, H2_max = H[param2].min()-0.5, H[param2].max()+0.5
    H1, H2 = np.meshgrid(np.arange(H1_min, H1_max, resolution),
                           np.arange(H2_min, H2_max, resolution))
    n = np.array([H1.ravel(), H2.ravel()]).T
    Z = model.predict(n)
    Z = Z.reshape(H1.shape)
    plt.contourf(H1, H2, Z, alpha=0.5, cmap="Set2")
    plt.xlim(H1_min, H1_max)
    plt.ylim(H2_min, H2_max)
    plt.xlabel("Length")
    plt.ylabel("Width")
    plt.scatter(H[param1],H[param2], c=M["花の種類"], cmap="brg")

関数が用意できたので、コチラを使って出力すると…

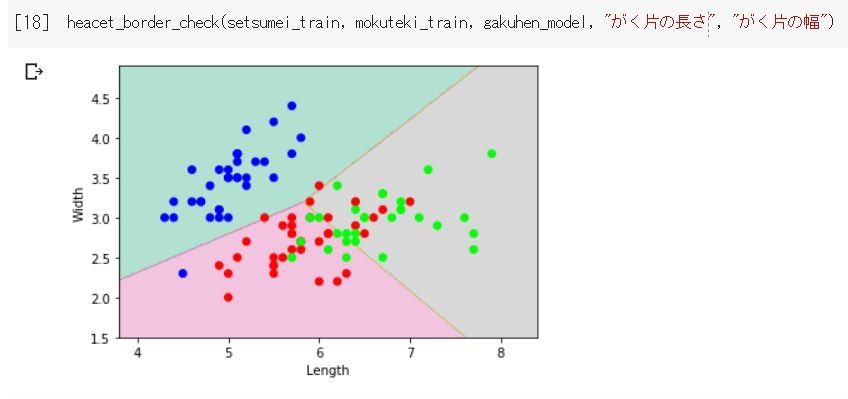
↑まずは上図が《がく片の長さと幅》を使った時の境界図です。
青丸は上手く境界を持てているようですが、赤丸と緑丸ごちゃごちゃしていて、微妙なところに境界線が引かれていますね。

そりゃあスコア低くなりますよね…という感じ。

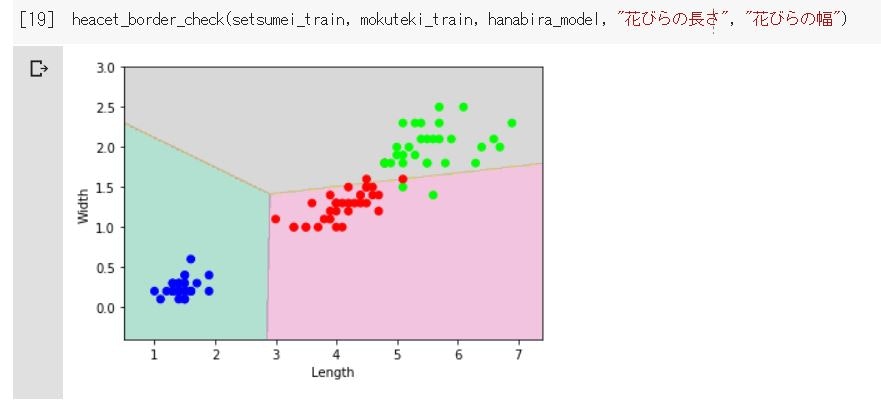
↑続いて上図が《花びらの長さと幅》を使った時の境界図です。
青丸は完璧ですね。赤丸と緑丸同士がほんの少し境界を越えているくらいで、ほぼ綺麗に境界線を引けていると思います。

がく片と花びらとで場合分けしてきましたが、『データの可視化によって特徴を選択することはとても重要なこと』は伝わったのではないでしょうか？

まとめ

最後まで見て頂きありがとうございました。

普段から技術記事は書いていないもので、少し口語が多かったかもしれません…笑

色々と調べながら初心者だからこその目線で《アヤメ分類》について一から説明してみました。

文書が変だったり、間違っている点などございましたら気軽にコメント頂けると嬉しいです。
もちろん感想やよかった点などでも気軽にコメントください(´艸｀*)