こんにちは、HerniaBabyです。普段はMATLAB Answersに生息しています。
MATLAB/Simulink Advent Calendar 2022 Advent Calendar 2022の12/24を担当します。
今回は Silent Night に向けて振動騒音を題材にしていこうと思います。
目次
はじめに
この記事は音の信号を「FFTしてくれや」って言われた時の手助けとなる事を目的とします。
ここでいうFFTとは経験上だいたいがパワースペクトルであり、「FFTしたのに複素数が出る!」と相談が来るので記事にしました。
紹介する手順は一例であり、組織によってやり方は異なると思います。
誤りがあれば@neginegaceにDMでこっそり教えてください…笑
(ここにコメントしていただいても大丈夫です)
データの用意
まずはデータセットから作りましょうか。ビルトインデータを使います。
clc,clear,close all;
wavFileList = dir('C:\program files\MATLAB\R2022b\**/*.WAV');
今回はエンジンノイズを使ってみましょう。
n = 113;
disp(wavFileList(n).name)
engine.wav
データの中身も簡単に見てみますか。音を聞きたい場合は soundsc を使ってください。
% 読み込み
filename = fullfile(wavFileList(n).folder,wavFileList(n).name);
info = audioinfo(filename);
x = audioread(filename);
% サンプリング周波数やブロックサイズ算出
Fs = info.SampleRate;
Num = info.TotalSamples;
t = ((0:Num-1)./Fs)';
図示します。
figure
plot(t,x,'Color',[.6 .6 .6])
xlabel '時間[s]'
ylabel '信号V'
title(wavFileList(n).name)
等価騒音レベルの計算
人間が知覚する音の大きさは必ずしも信号のパワーと一致しません。
人の耳はある種ハイパスフィルタのような特性を持っています。
なので補正する必要があるわけです。
A特性
今回はメジャーな方法であるA特性フィルタで補正します。
実はこの補正フィルタは関数で表記されており、Wikipediaにも載っています。
しかしながら英語版でないと式は書かれておりません。なんでや!
式はこんな感じ。
$R_A \left(f\right)=\dfrac{{12194}^2 f^4 }{\left(f^2 +20\ldotp 6^2 \right)\sqrt{\left(f^2 +107\ldotp 7^2 \right)\left(f^2 +77\ldotp 9^2 \right)}\left(f^2 +{1194}^2 \right)}$
$\begin{array}{l}
A\left(f\right)=20\log_{10} \left(R_A \left(f\right)\right)-20\log_{10} \left(R_A \left(1000\right)\right)
\approx 20\log_{10} \left(R_A \left(f\right)\right)+2\ldotp 00
\end{array}$
ちなみに当時Audio Toolboxを持っておらず、知識ゼロから勉強して作成した苦い思い出があります。
今ではMATLABパイセンの記事などで作成方法が紹介されたりと悩む事も減りました。
…開発が、ほんの少し遅ければHerniaBabyは---
Audio Toolboxを使い、関数を使って、快適に開発しただろう。
てなわけでweightingFilterを使います。
AWeighting = weightingFilter('A-weighting',Fs);
visualize(AWeighting,'class 1');

ここでわかると思うのですが、低周波域では音は大きく減衰されています。
そしてだいたい 2,000 Hz あたりでフィルタはピークをたどります。
フィルタを掛けてみましょう。
x_f = AWeighting(x);
図示します。
figure
hold on
plot(t,x,'Color',[.6 .6 .6])
plot(t,x_f,'r')
xlabel('時間[sec]')
ylabel('音信号[V]')
ylim([-1 1]*.6)
legend('original','A-weighted')
窓関数
MATLABで行うFFTその2 リーク誤差と窓関数で紹介しましたが軽く復習します。
信号に対してどんな周波数成分があるかわからない状態で、指定した区間を切り出してスペクトル解析を行います。
その時に端がピッタリ合っていないとリーク誤差が生じてしまいます。現実では避けられない誤差です。
その誤差を抑えるのが窓関数です。
ほんじゃあちょっとやってみっか!
figure
hold on
hw = hann(length(x_f));
plot(t,x_f,':','Color',[.7 .7 .7],'LineWidth',0.1);
plot(t,hw.*x_f,'r','LineWidth',0.8);
xlim([0 t(end)])
xlabel '時間[sec]'
ylabel '信号'
legend({'通常','窓付き'})
hold off
…ちょっと思いませんか?
「え?この信号を丸ごとFFTするんだっけ?」
そうなんですね、なのでだいたいは小区間に区切ってFFTして平均をとるんですね。
75%オーバーラップでハニングウィンドウをかけたFFT解析
オーバーラップとは
何個かセグメンテーション(窓あり)に分けて逐次FFTを掛けるような感じで、領域がかぶっていることをオーバーラップ量と言います。
だいたい50%~75%が相場な気がします。MathWorks社の stft が一番イメージしやすいかな。
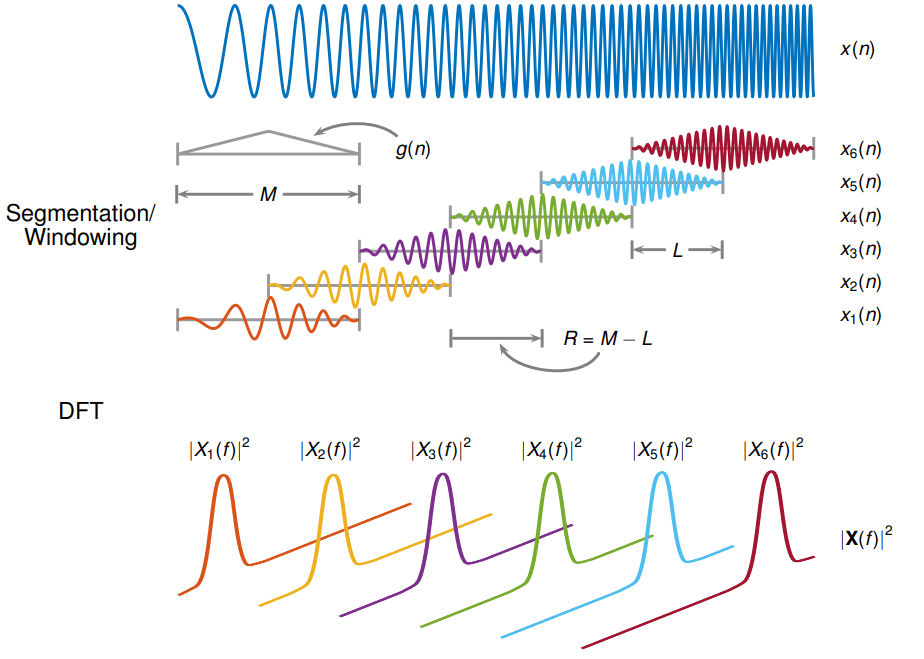
これに関してですが、人によってアプローチがあるんじゃないかなと思っています。
まずは時間周波数で見ることができる pspectrum の例を紹介します。
pspectrumでの解析
75%オーバーラップでリーケージ量を0.85としました。
これは75%オーバーラップのハニングウィンドウをかけたことに相当します。
[p1,f1,t1] = pspectrum(x,Fs,"spectrogram",'OverlapPercent',75,'Leakage',0.85);
[p2,f2,t2] = pspectrum(x_f,Fs,"spectrogram",'OverlapPercent',75,'Leakage',0.85);
時間周波数領域でA特を掛けた分だけ見てみましょう。
Sound Pressure Level (SPL)は以下のように表されます。
$SPL = 20 \log_{10}{\dfrac{p_{rms}}{p_0}}\lbrack dB \rbrack$
ここでpspectrumはパワーのため$P\left(f\right)={X\left(f\right)}^2$つまり振幅の実効値の二乗です。
$f$は片側スペクトルになっています。
[T2,F2] = meshgrid(t2,f2);
figure
surf(T2.*1e3,F2./1e3,20*log10(sqrt(p2)./20e-6),'EdgeAlpha',0)
colormap turbo
xlim([0 t2(end).*1e3])
ylim([0 f2(end)./1e3])
xlabel('時間[msec]')
ylabel('周波数[kHz]')
title('A特をかけた時間周波数領域のスペクトル')
c = colorbar;
c.Label.String = 'Sound Pressure Level [dBA]';
view(2)

低周波数の領域でうるさいのがわかりますね。
また定常的な振動をしていることも、ここで理解できます。
平均化
音圧レベルのパワー平均値は
$10\log_{10}{\biggl(\dfrac{1}{n}\dfrac{\Sigma{p^2_{rms}}}{p^2_0} \biggr)}
=20\log_{10}{\biggl(\dfrac{\sqrt{\bar{p}^2_{rms}}}{p^2_0} \biggr)}$
です。
figure
hold on
plot(f1,20.*log10(sqrt(mean(p1,2))./20e-6),'-','Color',[.5 .5 .5],'LineWidth',0.1) % 平均パワーレベル
plot(f2,20.*log10(sqrt(mean(p2,2))./20e-6),'-r','LineWidth',0.8) % 平均パワーレベル(A特)
legend('original','A-weighted')
xlabel('Frequency[Hz]')
ylabel('SPL[dB/dBA]')
title('75% Overlap ハン窓 SPL')
高周波側で落ちているのはA特性の影響です。
まあ平均化の部分はやや強引にやった気がしなくもないです。
ウェルチ法
この方法はある程度の長さがある白色雑音に対して、ランダム性を緩和するものです。
なので滑らかなパワースペクトル(密度)が得られます。
ここで(理由もなく)63分割し、オーバーラップ量は75%でスライドさせていきます。
Nx = length(x_f);
nsc = floor(Nx/63);
nov = floor(nsc*0.75);
規定値だとPSD(パワースペクトル密度)が算出されるので注意してください。周波数分解能分だけ小さくなります。
PSDとPS(パワースペクトル)の違いはパワースペクトルとパワースペクトル密度の違いがわかりやすいです。
[p_w1,f_w1] = pwelch(x,hann(nsc),nov,Fs,'power');
[p_w2,f_w2] = pwelch(x_f,hann(nsc),nov,Fs,'power');
図示します。
figure
hold on
plot(f_w1./pi.*(Nx/2),20.*log10(sqrt(p_w1)./20e-6),'-','Color',[.5 .5 .5],'LineWidth',0.1) % 平均パワーレベル
plot(f_w2./pi.*(Nx/2),20.*log10(sqrt(p_w2)./20e-6),'-r','LineWidth',0.8) % 平均パワーレベル(A特)
legend('original','A-weighted')
xlabel('Frequency[Hz]')
ylabel('SPL[dB/dBA]')
yticks(-40:10:80)
title('75% Overlap ハン窓 SPL ウェルチ法')
こちらの方がウィンドウサイズの調整やDFT長を設定できるのでお勧めかな。
終わりに
冒頭でも言いましたが…
「FFTしたら複素数とか意味わからんのが出るんやけど!」って半ギレ相談がきます。
どうして複素数か、ここらへんも別途記事にしていけたらなあと思います。
また本記事作成で分解能向上と計算高速化でゼロパディングFFTが使われていることを学びました。
これについては【FFT】正しい振幅が出るようなフーリエ変換のパラメタを考えるで紹介されています。
それでは良い聖夜を。