はじめに
今回は リーク誤差 と対策方法である 窓 の紹介をしていきます。
前回のあらすじ
前回の記事 では FFTで片側スペクトルの正規化 まで行いました。
しかし 狙った振幅よりも低い値 になってしまっていました。
今回はその原因と対策を書いていきます。
前回の復習
前回の復習から行いましょう。
Code
clear,clc,close all;
dt = 0.01;
L = 512;
t = 0:dt:dt*(L-1);
Fs = 1/dt;
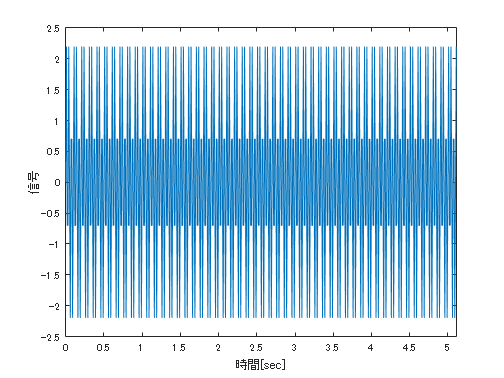
合成波について最大振幅は 10Hz で 0.5, 30Hz で 2 としています。
Code
y = .5*sin(2*pi*10*t) + 2*sin(2*pi*30*t);
plot(t,y)
xlim([0 t(end)])
xlabel '時間[sec]'
ylabel '信号'
ここでFFTして正規化まで行います。
Code
% FFT
cy = fft(y);
% 周波数(サンプリング周波数の半分だけ)
f = Fs*(0:(L/2))/L;
f = f(1:end-1);
% 正規化
P = abs(cy(1:ceil(length(cy)/2)))./(length(y)/2);
% 図示
stem(f,P)
hold on
% 10Hz付近, 30Hz付近の行を検索
idx = knnsearch(f',[10;30]);
scatter(f(idx),P(idx),'o')
name = P(idx)';
text(f(idx),P(idx)+0.1,cellstr(num2str(name)));
ylim([0 1.7])
xlabel '周波数[Hz]'
ylabel 'P1(f)'
hold off
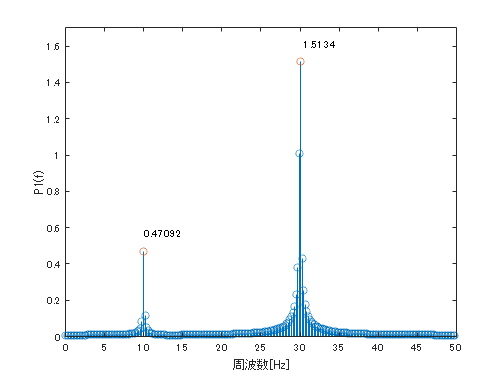
数字でピークをみてみましょう
Code
Peak = [f(idx)', P(idx)'];
fprintf('ピーク周波数 %-.2f Hz \t 振幅 %-.2f\n\n',Peak(1,:),Peak(2,:))
Output
ピーク周波数 9.96 Hz 振幅 0.47
ピーク周波数 30.08 Hz 振幅 1.51
んー、ずれてますねえ(ニッコリ)
10Hzはともかく、30Hz付近は過小評価されています。
リーク誤差
このずれはリーク誤差によって生じています。
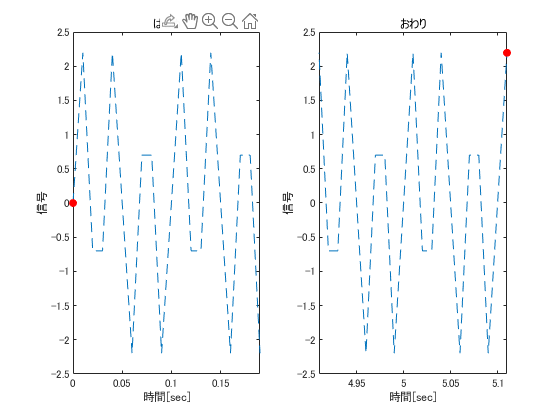
離散フーリエ変換は範囲を有限として、外側は範囲内の繰り返しとして仮定しています。
Code
subplot(1,2,1)
plot(t,y,'--')
hold on
scatter(t(1),y(1),'red','filled')
xlim([0 t(20)])
xlabel '時間[sec]'
ylabel '信号'
title 'はじめ'
subplot(1,2,2)
plot(t,y,'--')
hold on
scatter(t(end),y(end),'red','filled')
xlim([t(end-20) t(end)])
xlabel '時間[sec]'
ylabel '信号'
title 'おわり'
一致してませんね…これがリーク誤差の原因です。
つまり最初と最後がぴったし同じで繰り返さないとダメなんですね。
そんなん実践で毎回使えるやついる～？
対策：窓関数
じゃあどうするのか？偉い人は考えました。
最初と最後を0に収束させればよくね？！
そこで出てくるのが窓関数ってやつです。
ここではとりあえず迷ったら使えばいいと噂のハニング窓を使います。
Code
figure
hw = hann(length(y))';
plot(t,y,':','Color',[.7 .7 .7],'LineWidth',0.1); hold on
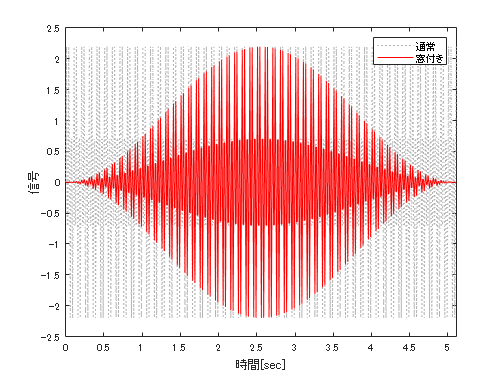
plot(t,hw.*y,'r','LineWidth',0.8);
xlim([0 t(end)])
xlabel '時間[sec]'
ylabel '信号'
legend({'通常','窓付き'})
hold off
こんな感じです
窓付きをFFTしますか。
ただここでも正規化が必要になります。
窓関数を使用した場合の正規化
窓関数を使った場合の正規化は以下のようになります。
$g\left(n\right)$：窓関数
$\textrm{nfft}$：ブロックサイズ
$\left|S\right|$：片側スペクトル
c\;=\;\frac{\Sigma \left(g\left(n\right)\right)}{\textrm{nfft}}
S_{\textrm{norm}} =\frac{\left|S\right|}{c\cdot \left(\textrm{nfft}/2\right)}
コードで書いてみましょう。
Code
% FFT
cy2 = fft(hw.*y);
% 正規化
c = sum(hw)/length(hw);
P = abs(cy2(1:ceil(length(cy2)/2)))./(length(y)/2)./c;
% 図示
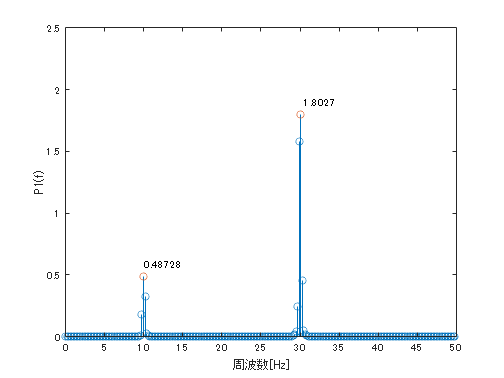
stem(f,P)
hold on
% 10Hz付近, 30Hz付近の行を検索
idx = knnsearch(f',[10;30]);
scatter(f(idx),P(idx),'o')
name = P(idx)';
text(f(idx),P(idx)+0.1,cellstr(num2str(name)));
ylim([0 2.5])
xlabel '周波数[Hz]'
ylabel 'P1(f)'
hold off
Code
Peak = [f(idx)', P(idx)'];
fprintf('ピーク周波数 %-.2f Hz \t 振幅 %-.2f\n\n',Peak(1,:),Peak(2,:))
Output
ピーク周波数 9.96 Hz 振幅 0.49
ピーク周波数 30.08 Hz 振幅 1.80
完ぺきではないですが、リーク誤差はある程度改善されました。
おわりに
次回はオーバーラップでもやろうかな。