【FFT】正しい振幅が出るようなフーリエ変換のパラメタを考える

はじめに

フーリエ変換の実装が分からなすぎてキレそうになっている．
今回はFFTに渡すデータ数を2のべき乗にした上で正しい振幅スペクトルを求める方法を簡単にメモした．

とりあえず言いたいのはフーリエ変換を実装しようとするとあまり意識せずにデータ数を256とか512とか1024にしがちなので，ΔFに注意する必要があるという点である．

フーリエ変換のサンプルコード

以下にフーリエ変換のサンプルが載っている．

高速フーリエ変換 - MATLAB fft - MathWorks

サンプルコードを少しだけ変えて以下のようにした．

Fs = 1000;            % Sampling frequency                    
T = 1/Fs;             % Sampling period       
L = 1500;             % Length of signal
t = (0:L-1)*T;        % Time vector

% 振幅0.7, 周波数50Hzのsin波
% 振幅1, 周波数120Hzのsin波
S = 0.7*sin(2*pi*50*t) + sin(2*pi*120*t);
X = S;

Y = fft(X);
P2 = abs(Y/L);
P1 = P2(1:L/2+1);
P1(2:end-1) = 2*P1(2:end-1);
f = Fs*(0:(L/2))/L;
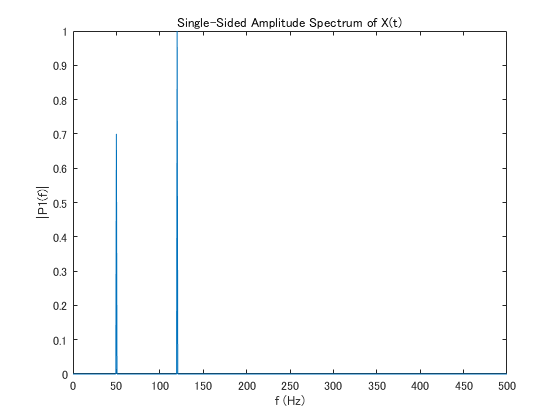
plot(f,P1) 
title('Single-Sided Amplitude Spectrum of X(t)')
xlabel('f (Hz)')
ylabel('|P1(f)|')

結果

フーリエ変換を行うと確かに希望する周波数のところに希望する振幅のスペクトルが立っていて嬉しい．

FFTに渡すべきデータ数

ところで，FFTをwikipediaると，以下のように書いてある．
高速フーリエ変換 - Wikipedia

高速フーリエ変換は、この結果を、次数Nが2の累乗のときに O(N log N) の計算量で得るアルゴリズムである。

FFTを行う場合に次数（データ数，NFFT）が2のべき乗だと良いらしいのである．

ここで，先ほど行ったフーリエ変換の次数は以下のようになっている．

length(X)
% = 1500

これは2のべき乗ではないので，FFTの計算速度が遅いみたいなのだ．
計算速度が遅いと嬉しくないので，これから改善策を検討する．

方法１　取り出すサンプル点数を減らして2のべき乗にする

サンプルデータは1500点あるので，それより少ない2のべき乗の1024点だけ取ってFFTにかける．

% 取り出す信号サイズを2のべき乗に減らす
L = 2^(nextpow2(length(S)) - 1);
X = S(1:L);

結果
結果は以下のようになった．赤線がデータ数を2のべき乗サイズに減らしたほうの振幅スペクトルである．精度が悪くなっており，スペクトルの裾野が広がっている．分析時間を短くしたので周波数分解能が悪くなるのは当然だが，それ以外にも理由はある．この辺は後ほど説明する．

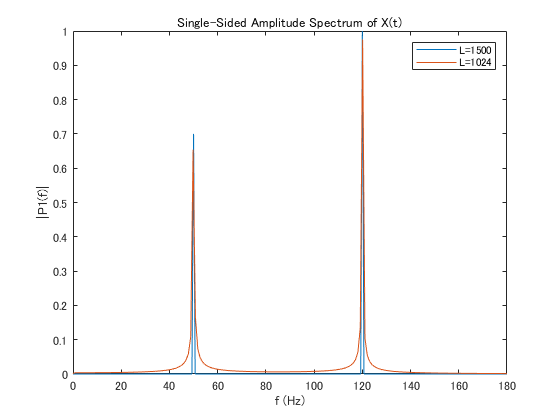
計算速度は向上しているものの，データ数が7割くらいに減っているので（速度向上するのは）それはそうという感じ．

% L = 1500
% 経過時間は 0.000225 秒です．
% L = 1024
% 経過時間は 0.000159 秒です．

試しに次数を2049, 2048にしたところ以下のようになった．
データ数が1個しか違わないのに3倍も速くなっていて偉いわね．

% L = 2049
% 経過時間は 0.000390 秒です．
% L = 2048
% 経過時間は 0.000118 秒です．

方法２　ゼロを付加してデータサイズを2のべき乗にする

データを減らすのではなく，増やす方向でやってみるやつである．

% 取り出す信号サイズを2のべき乗に増やす
L2 = 2^(nextpow2(length(S)));
X = [S zeros(1, L2 - L)]; % Sの後ろにゼロをつける
L = L2; % L を更新

結果
振幅が小さくなり，裾野も広がったように感じる．ピークのところにビヨーっと立っていたスペクトルがその周辺のビンにパワーを分散された形となった．

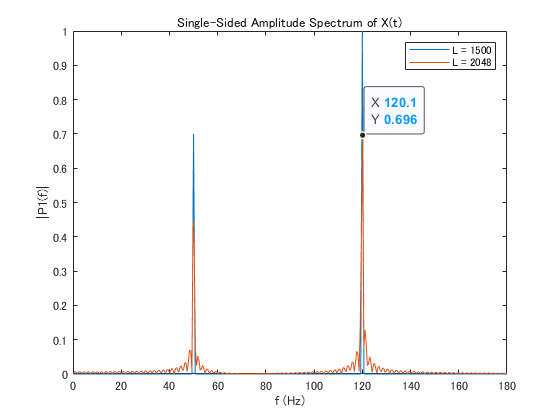
計算速度は良くなったんだけどね．

% L = 1500
% 経過時間は 0.000269 秒です．
% L = 2048
% 経過時間は 0.000110 秒です．

振幅が小さくなる問題についてはこちらに解説がある．
ゼロパディングFFTで高周波数分解能にするPythonコード

0をたくさん増やすとそれだけたくさんのビンにデータを振り分けるため，それぞれのビンのパワーは減っちゃうみたいな話か．
コードからもそれが分かる．ゼロパディングすると信号長Lがでかくなり，両側スペクトルP2を求める際にフーリエ変換の結果をLで割っているため，つまりP2が小さくなる．

P2 = abs(Y/L);

よって，ゼロパディング前後の信号長を補正にかけてやる．

% 取り出す信号サイズを2のべき乗に増やす
L2 = 2^(nextpow2(length(S)));
X = [S zeros(1, L2 - L)]; % Sの後ろにゼロをつける
X = L2 / L * X; % 振幅値を補正
L = L2; % L を更新

結果は以下のようになり，補正したはずなのに振幅値が若干小さくなっており，微妙である．

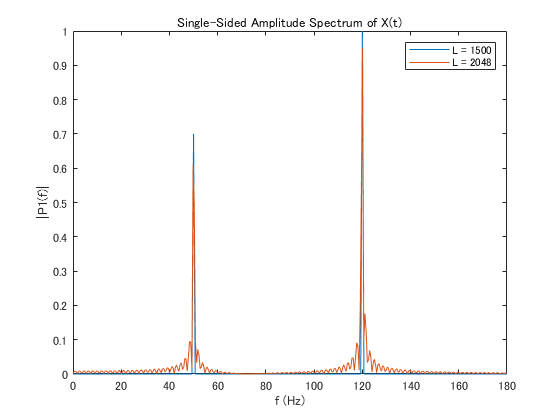
⊿Fを考慮する

ΔFを表示

こうなってしまう原因としては，ΔFが微妙な感じになっているせいである．
ここでΔFを見てみる．

% dfを確認する
dF = 1/(length(X)/Fs);
fprintf("Fs = %d, L = %d\n", Fs, length(X));
fprintf("dF = %f\n", dF);
fprintf("rem(50Hz, dF) = %f\n", rem(50, dF));
fprintf("rem(120Hz, dF) = %f\n", rem(120, dF));

% Fs = 1000, L = 1500
% dF = 0.666667
% rem(50Hz, dF) = 0.000000
% rem(120Hz, dF) = 0.000000

% ゼロパディング後
% Fs = 1000, L = 2048
% dF = 0.488281
% rem(50Hz, dF) = 0.195313
% rem(120Hz, dF) = 0.371094

信号の周波数50, 120HzがΔFの倍数でないために，適切なビンが存在せず，複数のビンに振り分けられちゃってるというわけである．だから裾野が広がったのだ．

方法３　ΔFを考慮したリサンプリングを行う

上記の話から，ΔFを変えないようにしたほうが無難でありそうだ．

ここで，フーリエ変換の不確定性原理からΔF×ΔT = 一定であり，ΔTは分析するデータの秒数である．

今まで分析するデータ数を減らしたり増やしたりしてきたが，これは言い換えると分析する秒数を変化させる操作となる．例えば2秒間のデータを0～1秒部分だけ分析したり，1秒分の無音データをくっつけて3秒間のデータとして分析したりという操作だ．

2秒間のデータを分析すると，ΔF=1/2＝0.5Hzとなり，3秒間のデータだとΔF=1/3＝0.33Hzとなる．

よって，ΔFを変えてはいけないならばΔTも変えてはいけないわけである．

ここでデータ数はΔT×Fsで決定される．
ΔFもΔTも変えずにデータ数を変更したかったら，Fsを変えればいいということである．

ここでサンプルコードに戻ると，Fs = 1000Hzであり，データ数は1500であった．つまりΔT=1.5秒であり，これを変えないようにFsを調整する．

等間隔でサンプリングされている信号のリサンプリング

% リサンプリング処理
dT = L / Fs;% 分析する時間長，これは変えちゃ駄目
newFs = 2048 / dT;% NFFT=2048となるようにFsを変更
newL = newFs * dT; % これが2のべき乗となるようにする
[p, q] = rat(newFs / Fs);
newS = resample(S,p,q);
% 各値を更新
Fs = newFs;                 
T = 1/Fs;
t = (0:L-1)*T;
L = newL;
S = newS;

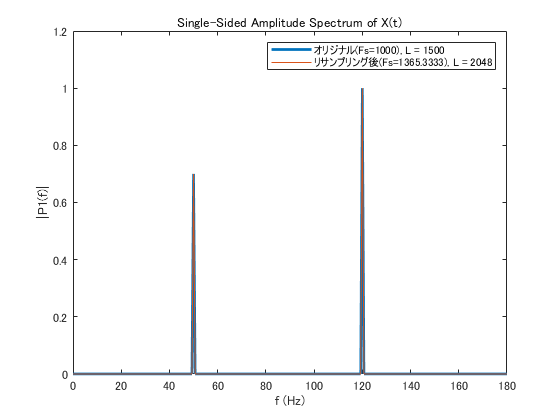
この例だと新しいFs=1.3653e+03となった．サンプリング周波数が整数じゃなくてキモい感じだが，しょうがない．

結果

リサンプリング後のフーリエ変換の結果は振幅が正しく出ており，満足する結果となった．

なお，計算時間はめっちゃ遅くなった．
キリの悪い次数をFFTするよりも，「リサンプリング処理+キリの良い次数でFFT」のほうが時間がかかるということである．
キレそう～．

% オリジナル
% L = 1500
% 経過時間は 0.001783 秒です．
% リサンプリング
% L = 2048
% 経過時間は 0.065089 秒です．

ΔFを変えてみる

今まではΔFは変えないほうがいいと言ってきたが，目的の周波数がビンに一致するのであれば，変えちゃっても問題ない．

今回はサンプルコードを使ったのでΔF=0.667Hzであったが，業務でスペクトル分析を行う場合は，ΔF=1Hz（とか10Hzとか0.1Hz）みたいなキリのいい数値で分析することが多い．
ということで，ΔF=1Hzで分析してみることにする．これならば目的の周波数50, 120Hzはビンに一致するので良い．

% リサンプリング処理
dF = 1;%とする
dT = 1 / dF;
newFs = 2048/ dT;
newL = newFs * dT;
[p, q] = rat(newFs / Fs);
newS = resample(S,p,q);

結果
結果は以下のようになり，正しい振幅が得られた．

まとめ

今回はFFTに渡せるようデータ数が2のべき乗となるようにした上で，正しい振幅スペクトルを求めるための方法をいくつか検討した．

データ数を減らすまたはゼロパディングする処理は正しい振幅が出なかったが，計算速度は速くなった．
リサンプリングを行う処理では正しい振幅が出たが，計算速度が遅くなった．
普通のフーリエ変換の時間計算量はO(N^2)，データ量が2のべき乗だとO(Nlog(N))だそうなので，リサンプリング処理の時間計算量がいくらかは知らないが，データ数がめちゃくちゃ多くなるとリサンプリング処理にしたほうが速くなる可能性はある．

ユーザーから見ると，FFT点数などは（プログラミングの実装の問題なので）ぶっちゃけどうでもよく，興味があるのはΔFやΔTである．
ユーザーは「N=256で分析したい！」という感じではなく，「ΔF=1[Hz]で分析したい！」と考えているわけである．

↑こういう音楽再生アプリのビジュアライザ機能のようにスペクトルをオシャレ表現として使うならΔFがどうだろうがあまり関係ないが，周波数解析ソフトとしてきっちりとした結果を出す場合は，この辺を意識する必要がある．
実装する側はΔFなどをユーザーが指定した値となるように，そして計算速度が速くなるようにいい感じのアルゴリズムを考えていかなければならない．

また，そういう点からすると今回参考にしたmatlabのサンプルも宜しくない．サンプリング点数Lを自分で指定しているからだ．L=1500と言われても，サンプリング周波数が変わればその意味合いも変わってくる．サンプリング点数ではなく，時間や周波数を指定したほうがいいように思われる．

Fs = 1000;                
T = 1/Fs;       
L = 1500;         % 信号のサンプリング点数を入力値として指定している
t = (0:L-1)*T;

% ↓のように書き換える

Fs = 1000;             
T = 1/Fs; 
T1 = 1.5;         % 信号の秒数を指定する    
L = Fs * T1;      % サンプリング点数は秒数から計算する
t = (0:L-1)*T;
%
%
% 余談
% tの計算は変える必要が無いが，
% 個人的にはこっちの書き方のほうがすき（宗派の違い）
t = ((1:L)-1)/Fs;