1. はじめに
R言語は、データ解析専用のオープンソース・フリーソフトウェアです。
Rでクラスタリングを用いたデータ分析方法を紹介します。
2. 準備
まずは、R言語を使用するためにR Statio (またはR言語)をインストールします。
インストールイメージは、以下のリンク先からダウンロードできます。
・R Studio ・・・https://www.rstudio.com/products/rstudio/download/
・R ・・・https://cran.r-project.org/index.html
R StudioはR実行のための統合開発環境(IDE)です。
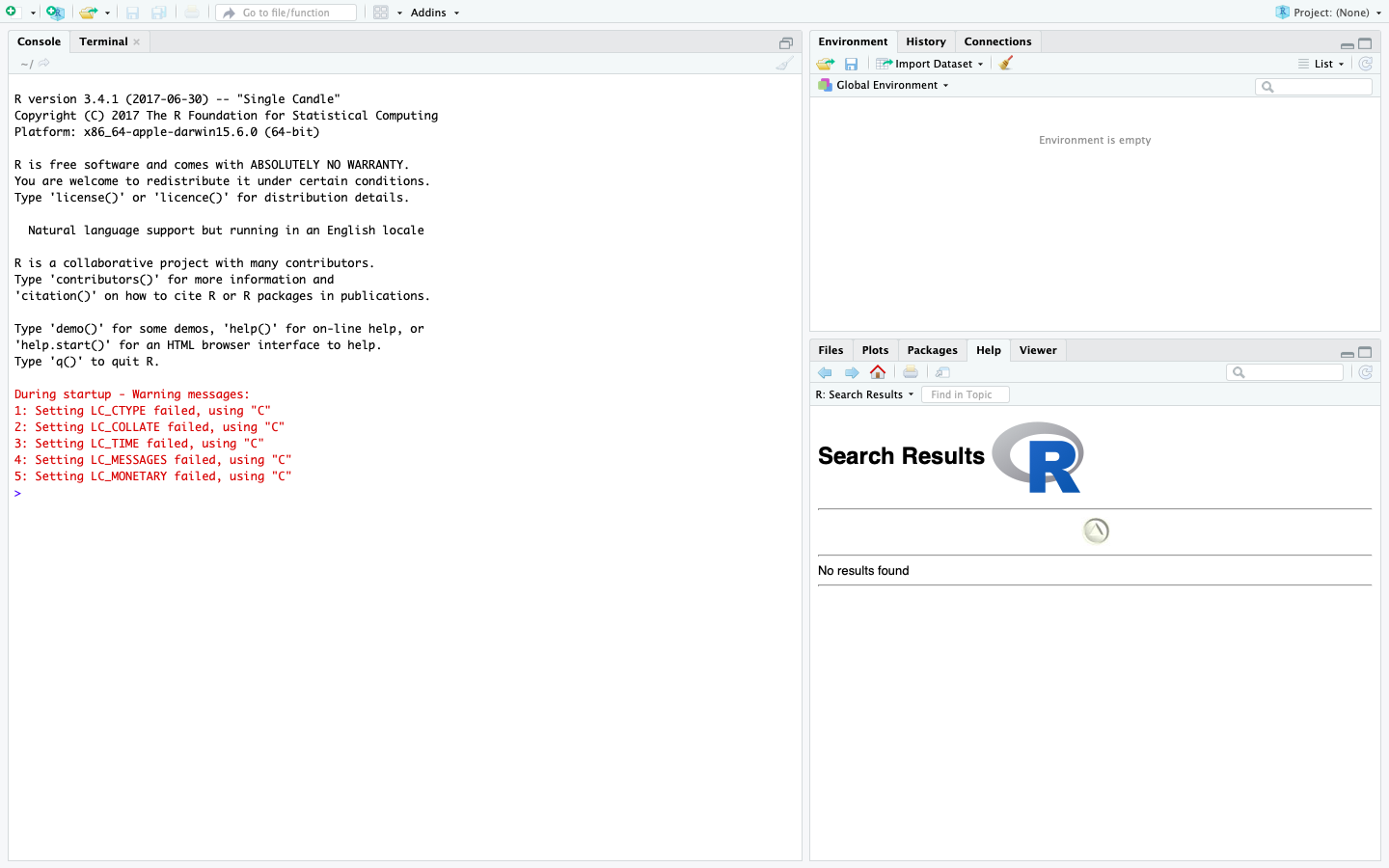
R Studioを起動すると以下のような画面が表示されます。
基本的な操作としては、上記に示されるR Studio画面の左側「Console」ウィンドウにコードを打ち、対話形式で処理を進めていきます。
ためしに、以下のような簡単な計算を打ってみてください。
> x = 1+1
> x
実行すると、xに代入された計算結果が返されます。
[1] 2
3. クラスタリングとは
Rで実行する前に、クラスタリングについて解説します。
**クラスタリング(クラスター分析)**とは、データの類似度をもとにデータをいくつかのクラスター(グループ)に分けるデータ分析手法です。
教師なし学習の代表的手法の一つで、正解データは与えられず、入力されたデータからパターンを見つけ出します。
クラスタリングにおけるデータの類似度は、データ間の距離に基づきます。
距離の求め方としては、ユークリッド距離がよく使用されます。
以下に、いくつか距離の種類を示します。
・ユークリッド距離(Euclidean)
・ミンコフスキー距離(Minkowski)
・マンハッタン距離(Manhattan)
・マハラノビス距離(Mahalanobis)
・チェビシェフ距離(Chebyshev)
・キャンベラ距離(Canberra)
また、クラスタリングのなかでも、大きく分類して、以下2種類の手法があります。
・階層クラスタリング
・非階層クラスタリング
第3項から、この2種類のクラスタリングについて、それぞれ解説します。
3-1. 階層クラスタリング
階層クラスタリングについて解説します。
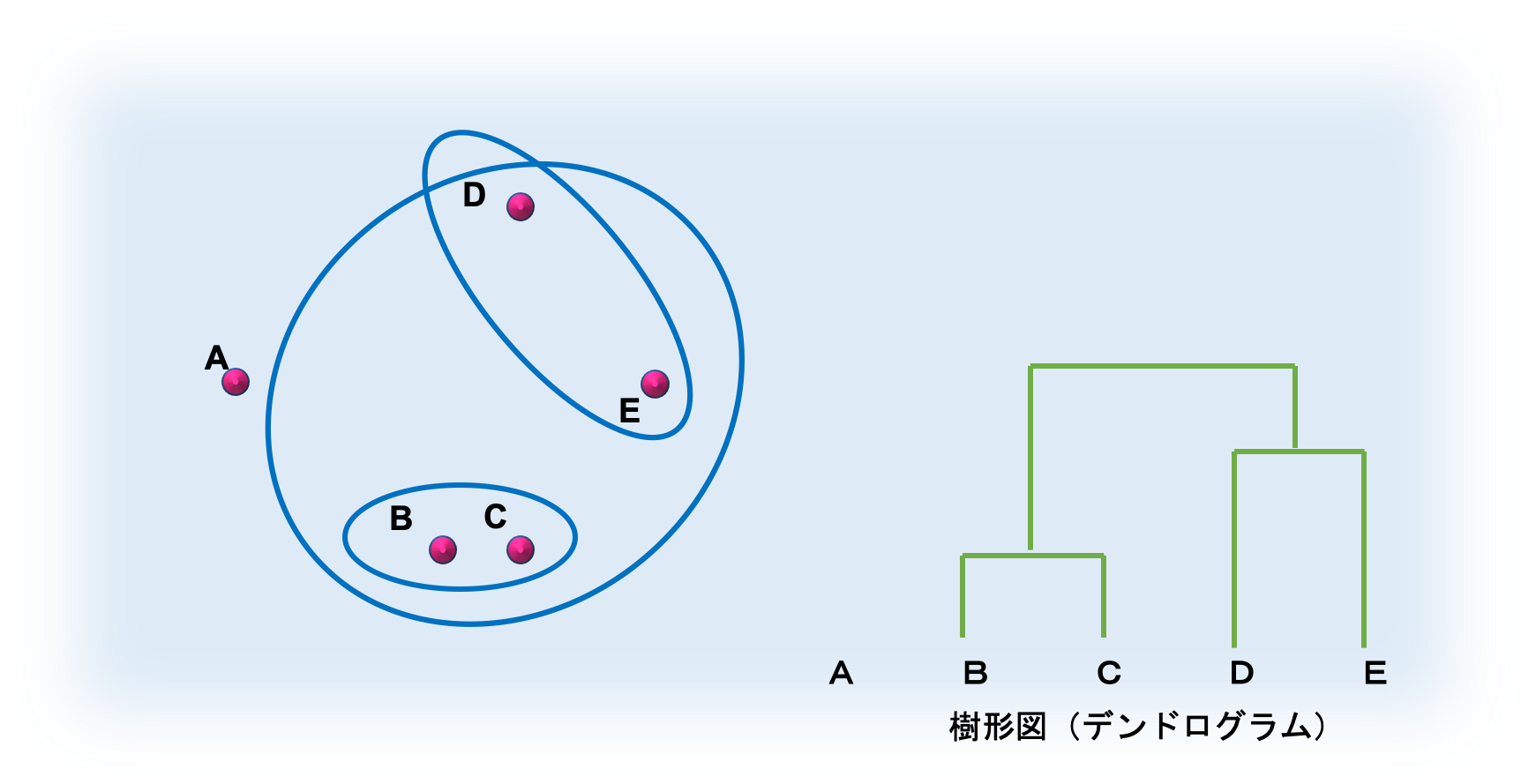
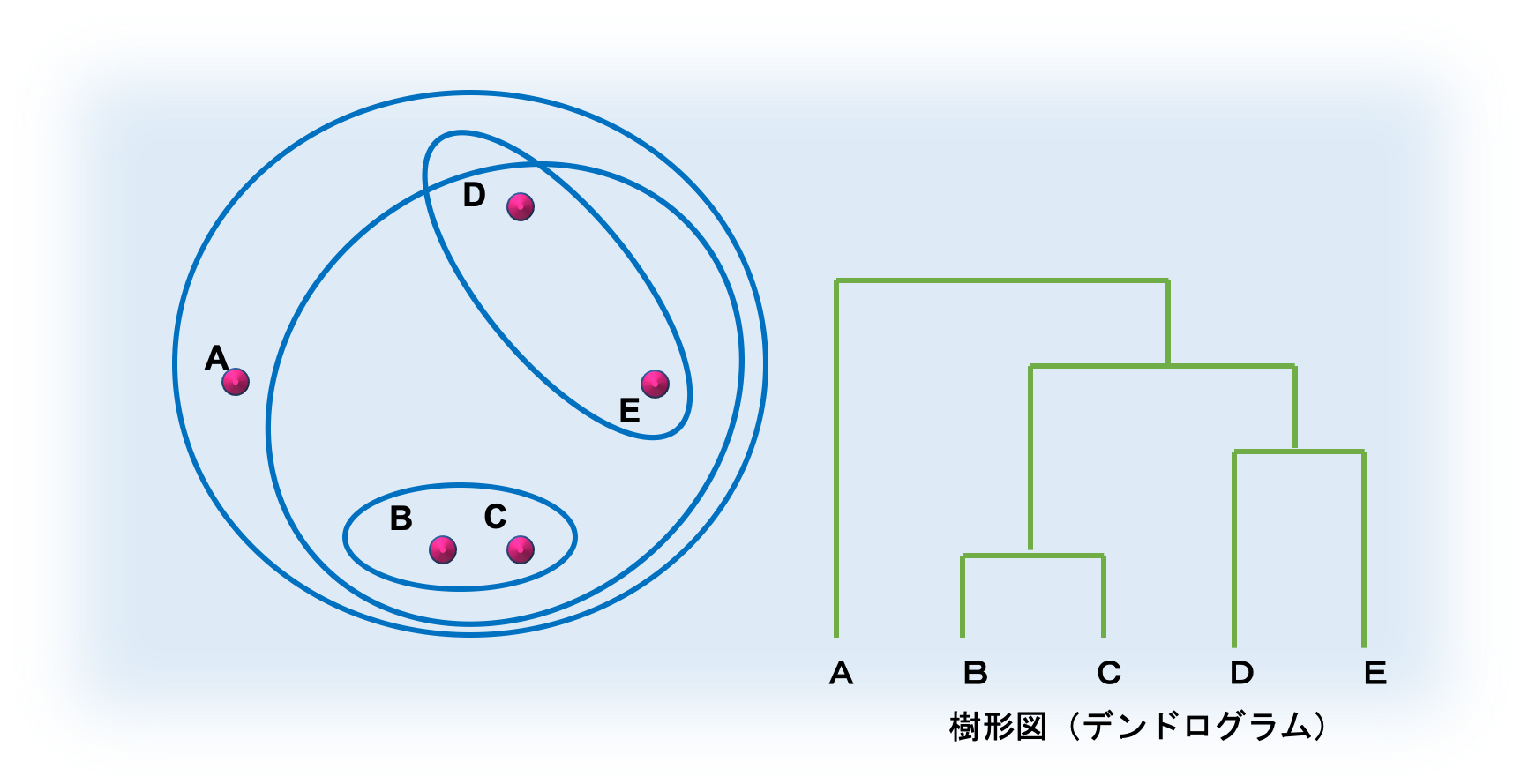
階層クラスタリングでは、まず似ている組み合わせを順番にまとめていき、**樹形図(デンドログラム)**を作成します。
そして、出来上がった樹形図をもとにデータをクラスターに分割します。
手順は、以下の通りになります。
■ 手順
① 1個の対象データのみ含む N 個のクラスターを作成する (N・・・データの個数)
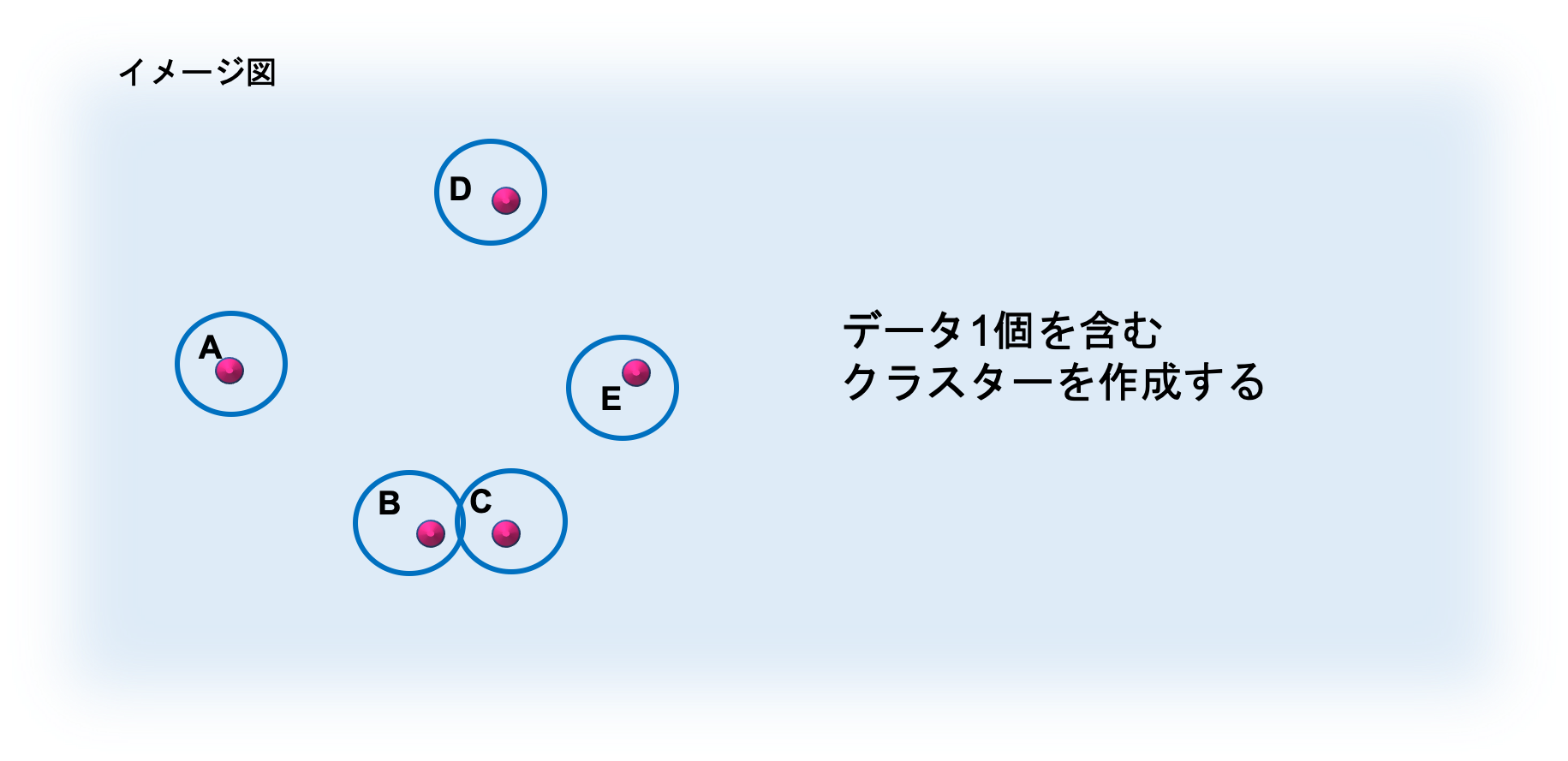
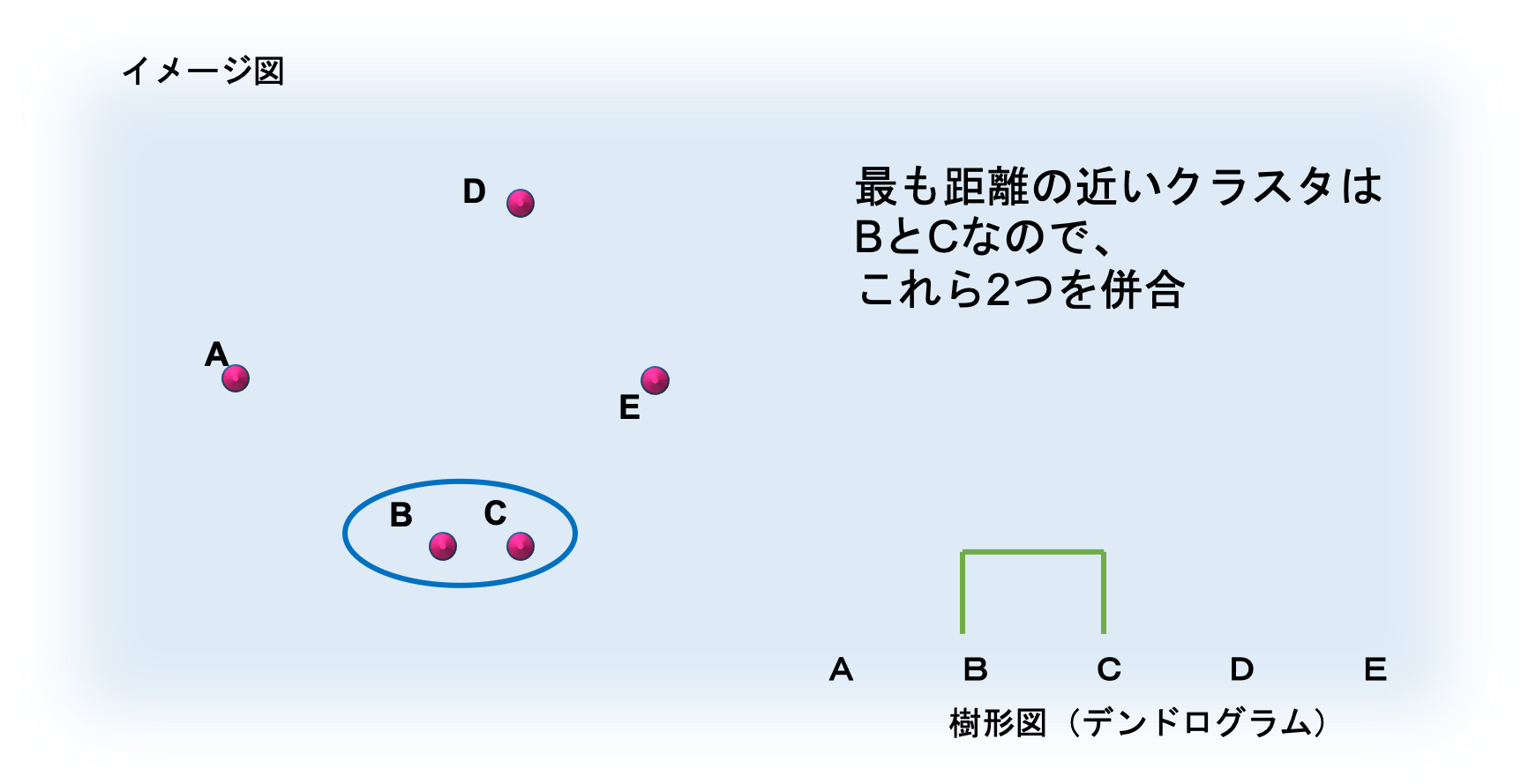
② 対象データ x1 と x2 の間の距離 d(x1,x2) からクラスター間の距離 d(C1,C2) を計算し,最もこの距離の近い二つのクラスターを逐次的に併合する
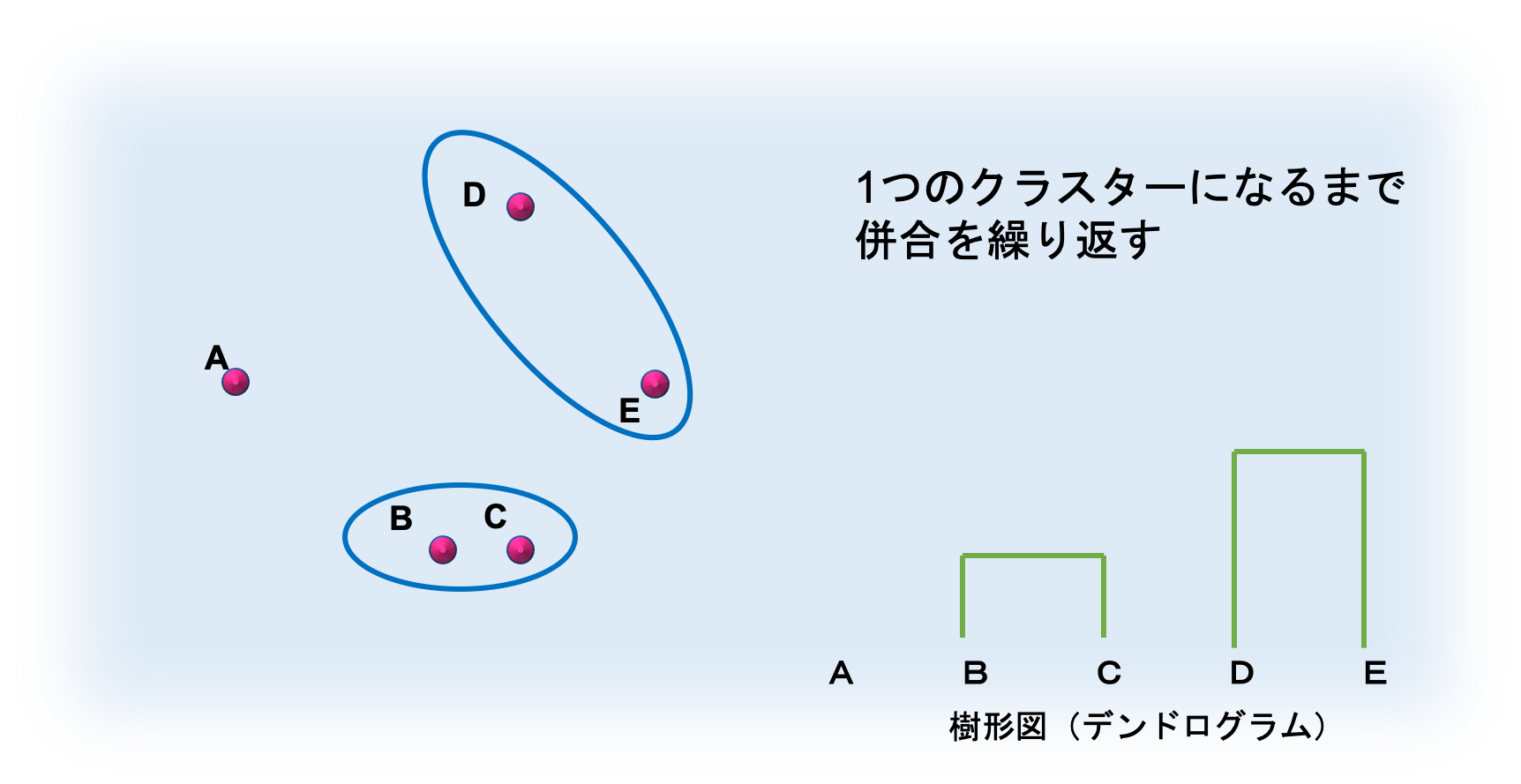
③ すべての対象が1つのクラスターに併合されるまで②を繰り返す
対象の類似度を計測する時、クラスター間の距離を測定しますが、この距離の測定方法には、以下のような方法があります。
| 方法 | 説明 |
|---|---|
| 最短距離法(単連結法) | 2つのクラスターから1個ずつ個体を選び、個体間の距離を求め、最も近い個体間の距離をクラスター間の距離とする. |
| 最長距離法(完全連結法) | 2つのクラスターから1個ずつ個体を選び、個体間の距離を求め、最も遠い個体間の距離をクラスター間の距離とする. |
| 群平均法 | 最近隣法と最遠隣法のハイブリッド的な手法. 全個体間の距離の平均をクラスター間の距離とする. |
| 重心法 | クラスター間の重心間距離をクラスター間の距離とする. 重心を求める際に、個体数を重みとして用いる. |
| メディアン法 | 重心法と似た方法。重みを等しくし求めたクラスター間の重心間距離をクラスター間の距離とする. |
| McQuitty 法 | 2つのクラスターA・Bを併合したクラスターCがある時、クラスターDとの距離を、距離ADと距離BDの平均値より算出する. |
| ウォード法(最小分散法) | 併合することによる情報の損失量の増加分をクラスター間の距離とする. すべてのクラスター内の偏差平方和の和が小さくなるように併合する. |
この中では、ウォード法が最もよく使用されます。
3-2. 非階層クラスタリング
非階層クラスタリングについて解説します。
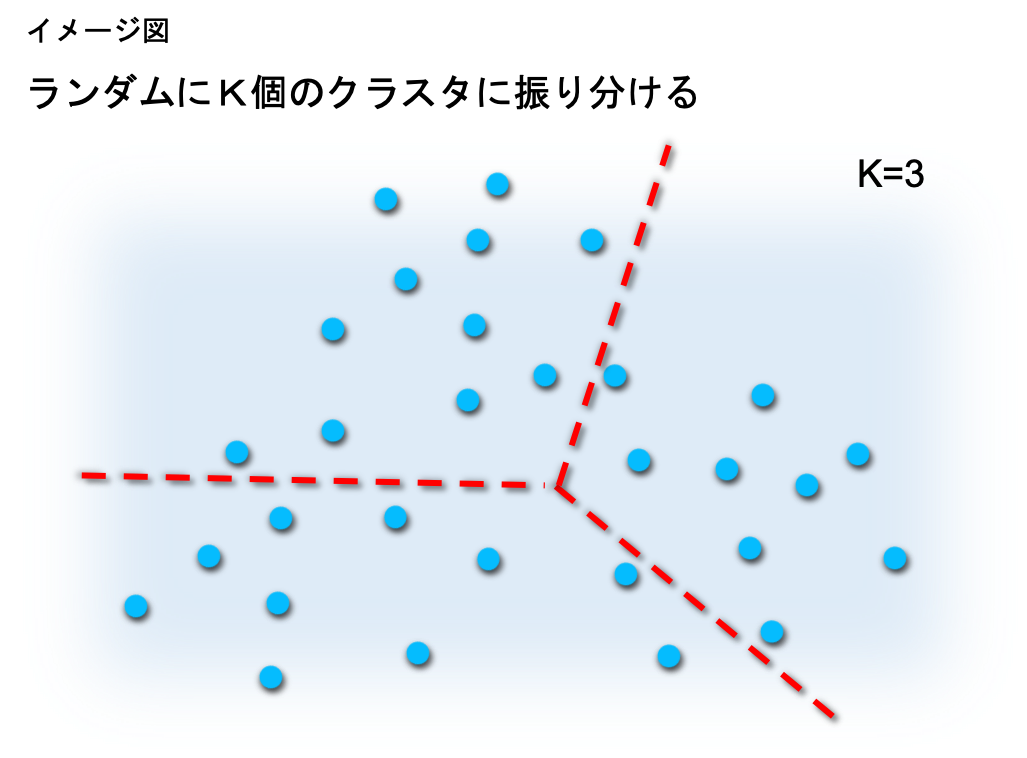
非階層クラスタリングは、いくつのクラスターに分類するかをあらかじめ決めておき、サンプルを分割していく手法です。
手順は、以下の通りになります。
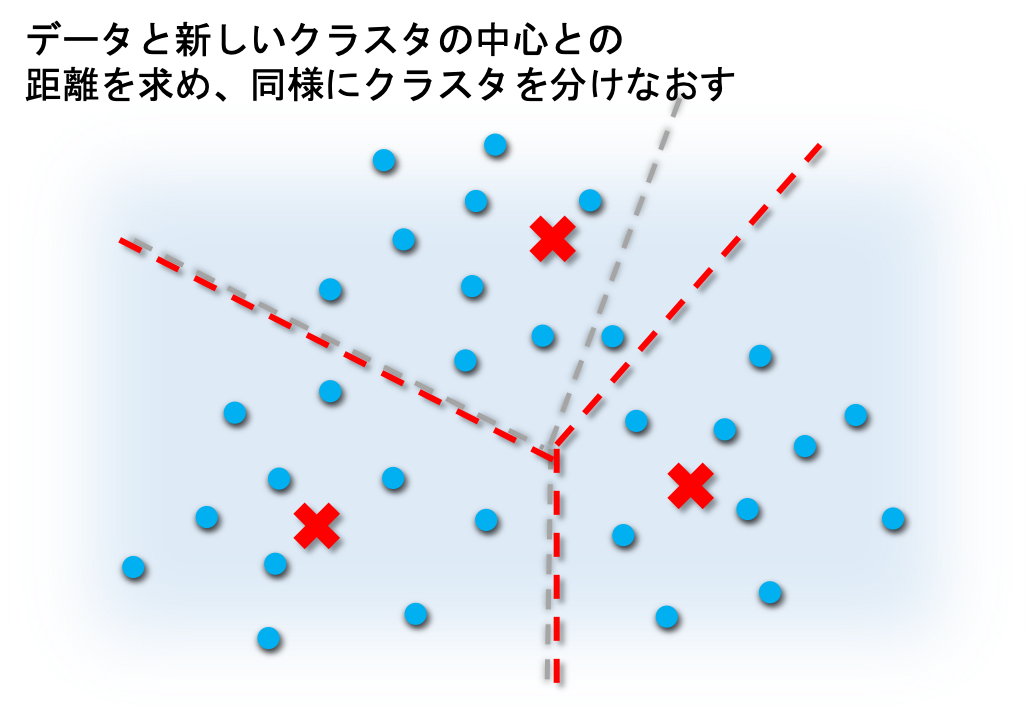
② すべてのデータ と 各クラスターの中心 との距離を求め、データを最も近いクラスターに振り分け直す。
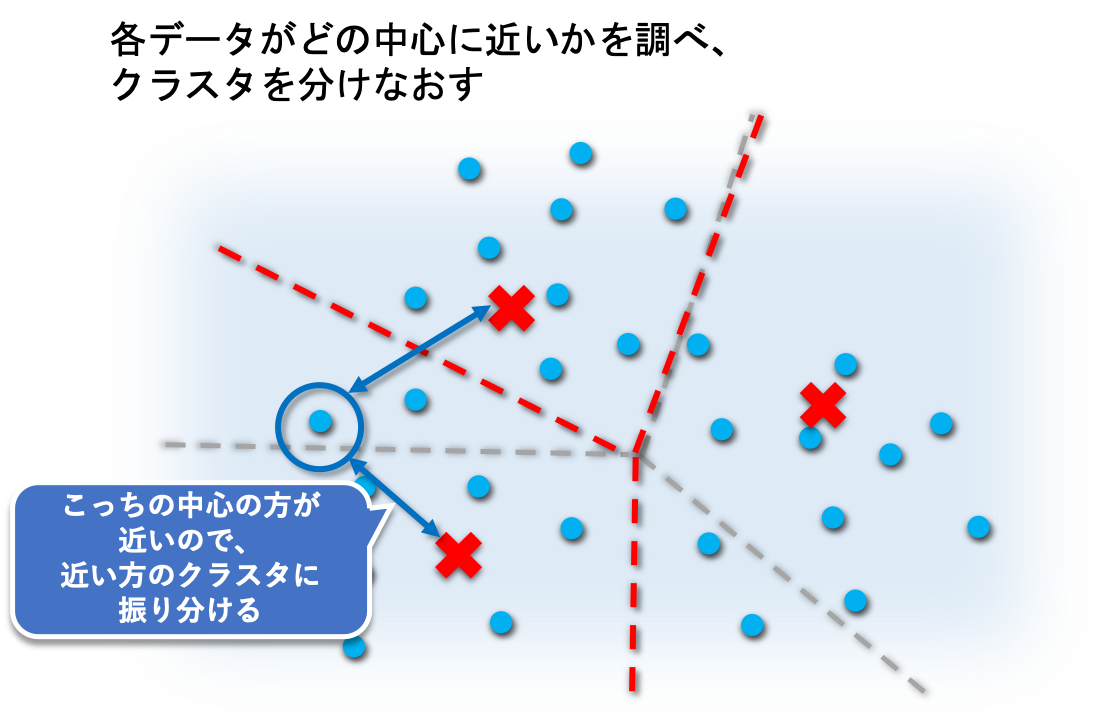
③ 新しく作成されたクラスターの中心を求める。
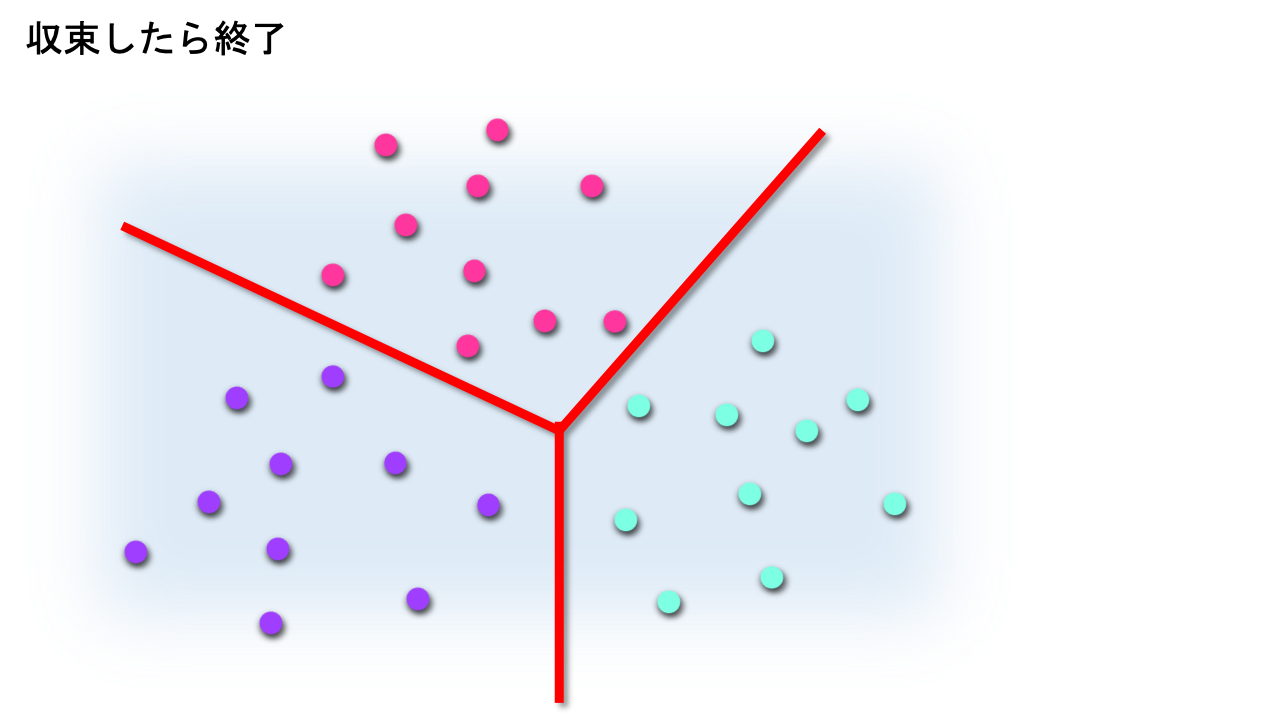
④ 結果が収束するか、あらかじめ設定した 繰り返し回数の最大値 に達するまで、手順②・③を繰り返す。
非階層クラスタリングの代表的な手法が、k-means法 です。
第5項では、k-means法を用いたRでのクラスタリング方法を紹介します。
4. データセット
Rには、あらかじめいくつかデータセットが準備してあります。
ここでは、Rでクラスタリングを実行する際に使用するデータセットについて説明します。
4-1. データ確認
今回、使用するデータセットは irisデータです。
irisデータには、3種類のアヤメのサンプルデータが含まれています。
データの中身は、コンソール上で "iris"と打つと確認できます。
> iris
Sepal.Length Sepal.Width Petal.Length Petal.Width Species
1 5.1 3.5 1.4 0.2 setosa
2 4.9 3.0 1.4 0.2 setosa
3 4.7 3.2 1.3 0.2 setosa
4 4.6 3.1 1.5 0.2 setosa
5 5.0 3.6 1.4 0.2 setosa
6 5.4 3.9 1.7 0.4 setosa
~~~~~(省略)~~~~~
後ほどクラスタリングに使用するため、変数data に、irisデータの1~4列を入力しておいてください。
> data <- iris[,1:4]
> head(data)
Sepal.Length Sepal.Width Petal.Length Petal.Width
1 5.1 3.5 1.4 0.2
2 4.9 3.0 1.4 0.2
3 4.7 3.2 1.3 0.2
4 4.6 3.1 1.5 0.2
5 5.0 3.6 1.4 0.2
6 5.4 3.9 1.7 0.4
4-2. データ構造
irisデータの構造を確認します。
データ構造を確認すると、以下の通りです。
> str(iris)
'data.frame': 150 obs. of 5 variables:
$ Sepal.Length: num 5.1 4.9 4.7 4.6 5 5.4 4.6 5 4.4 4.9 ...
$ Sepal.Width : num 3.5 3 3.2 3.1 3.6 3.9 3.4 3.4 2.9 3.1 ...
$ Petal.Length: num 1.4 1.4 1.3 1.5 1.4 1.7 1.4 1.5 1.4 1.5 ...
$ Petal.Width : num 0.2 0.2 0.2 0.2 0.2 0.4 0.3 0.2 0.2 0.1 ...
$ Species : Factor w/ 3 levels "setosa","versicolor",..: 1 1 1 1 1 1 1 1 1 1 ...
irisデータの構造を簡単にまとめると、以下のようになります。
| 変数名 | データ型 | 説明 |
|---|---|---|
| Sepal.Length | num | アヤメのがく片の長さ |
| Sepal.Width | num | アヤメのがく片のの幅 |
| Petal.Length | num | アヤメの花びらの長さ |
| Petal.Width | num | アヤメの花びらの幅 |
| Species | Factor | アヤメの品種 |
さらに、データの行数 と 品種別のデータ数 を確認します。
> nrow(iris)
[1] 150
> summary(iris$Species)
setosa versicolor virginica
50 50 50
つまり、このデータセットは全体数が150サンプルであり、そのうち、アヤメの3つの品種(setosa、versicolor、virginica)にそれぞれ50ずつサンプルが含まれることがわかります。
第5項より、変数dataに入力したアヤメのサンプルデータを用いて、Rでクラスタリングを実行します。
5. 実行
第4項で説明したirisデータを使用して、クラスタリングを実行します。
データセットには、setosa・versicolor・virginicaの3品種のアヤメのサンプルデータがありました。
ここでは、クラスタリングを用いて、アヤメの がく片・花びら の 長さ・幅(Sepal.Length、Sepal.Width、Petal.Length、Petal.Width) をもとに3つのクラスタに分割し、アヤメの品種別での分類を試みます。
クラスタリング後には、結果とデータセットのSpeciesを照らし合わせ、どれくらい正確にアヤメを品種別に分類できたかを確認します。
5-1. 階層クラスタリング
階層クラスタリングで、irisデータの分類を行います。
まず最初に、irisデータの樹形図を作成します。
樹形図の作成には関数 hclust を使用します。
関数 hclust の書式と引数は以下の通りです。
hclust(d, method = "使用メソッド")
| 引数 | 説明 |
|---|---|
| d | 関数 dist 作成した非類似度 |
| method | 使用するクラスター間の距離測定メソッド |
Rではクラスター間の距離測定メソッドとして、以下表に示す方法が使用できます。
任意の方法を関数 hclust の引数 method に指定することで、その方法を用いたクラスタリングが実行できます。
| 方法 | 引数methodで設定する文字列 |
|---|---|
| 最短距離法(単連結法) | single |
| 最長距離法(完全連結法) | complete |
| 群平均法 | average |
| 重心法 | centroid |
| メディアン法 | median |
| McQuitty 法 | mcquitty |
| ウォード法(最小分散法) | ward.D2 |
実際に関数 hclust を実行します。
データの非類似度を 関数 dist で求め、変数 distance に入力します。
そして、関数 hclust の引数 d に、distance を指定します。
今回はウォード法を使用するので、引数 method には "ward.D2"を指定します。
# 非類似度(距離)を計算
> distance <- dist(data) #ユークリッド距離を求める
# 樹形図作成
> hc <- hclust(distance, "ward.D2")
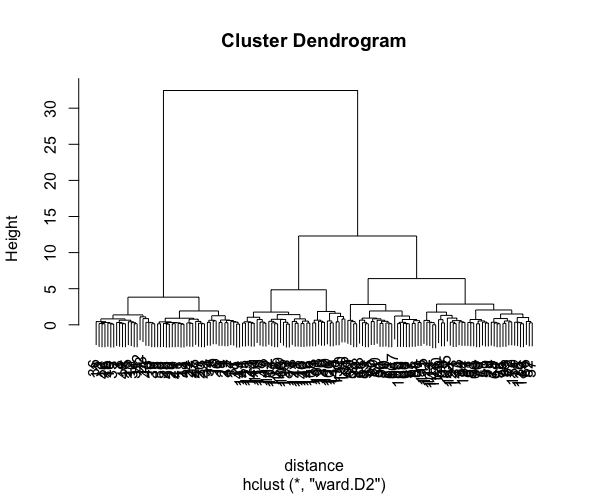
樹形図をプロットすると以下のようになります。
# デンドログラム プロット
> plot(hc)
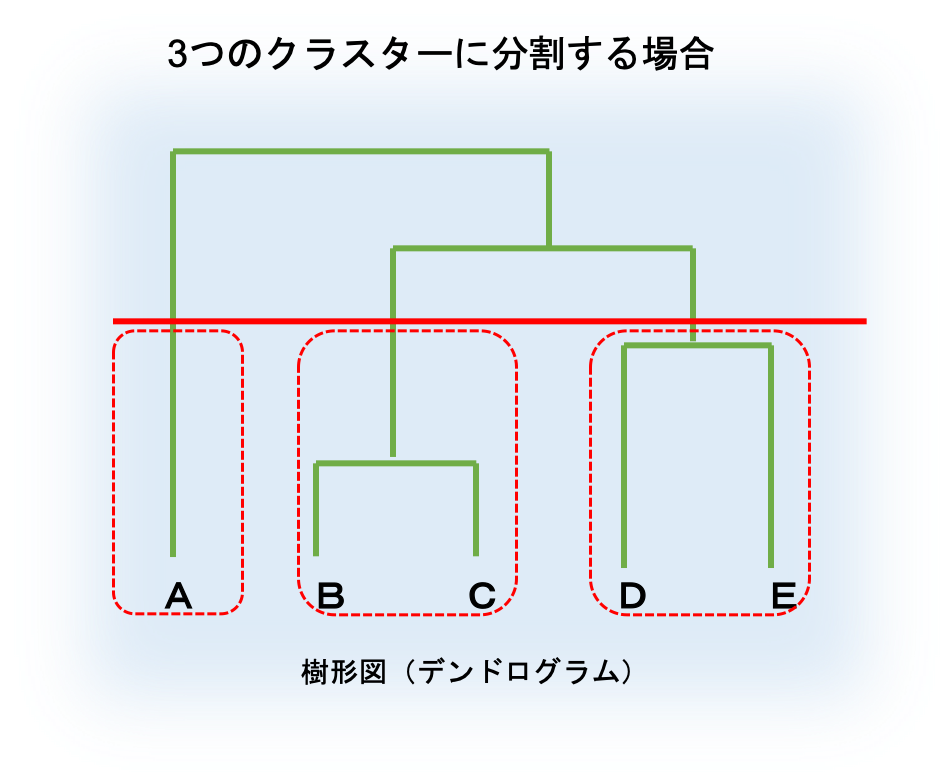
次に、取得した樹形図をもとに、データを3つのクラスターに分割します。
分割するイメージとしては、以下の図の通りです。
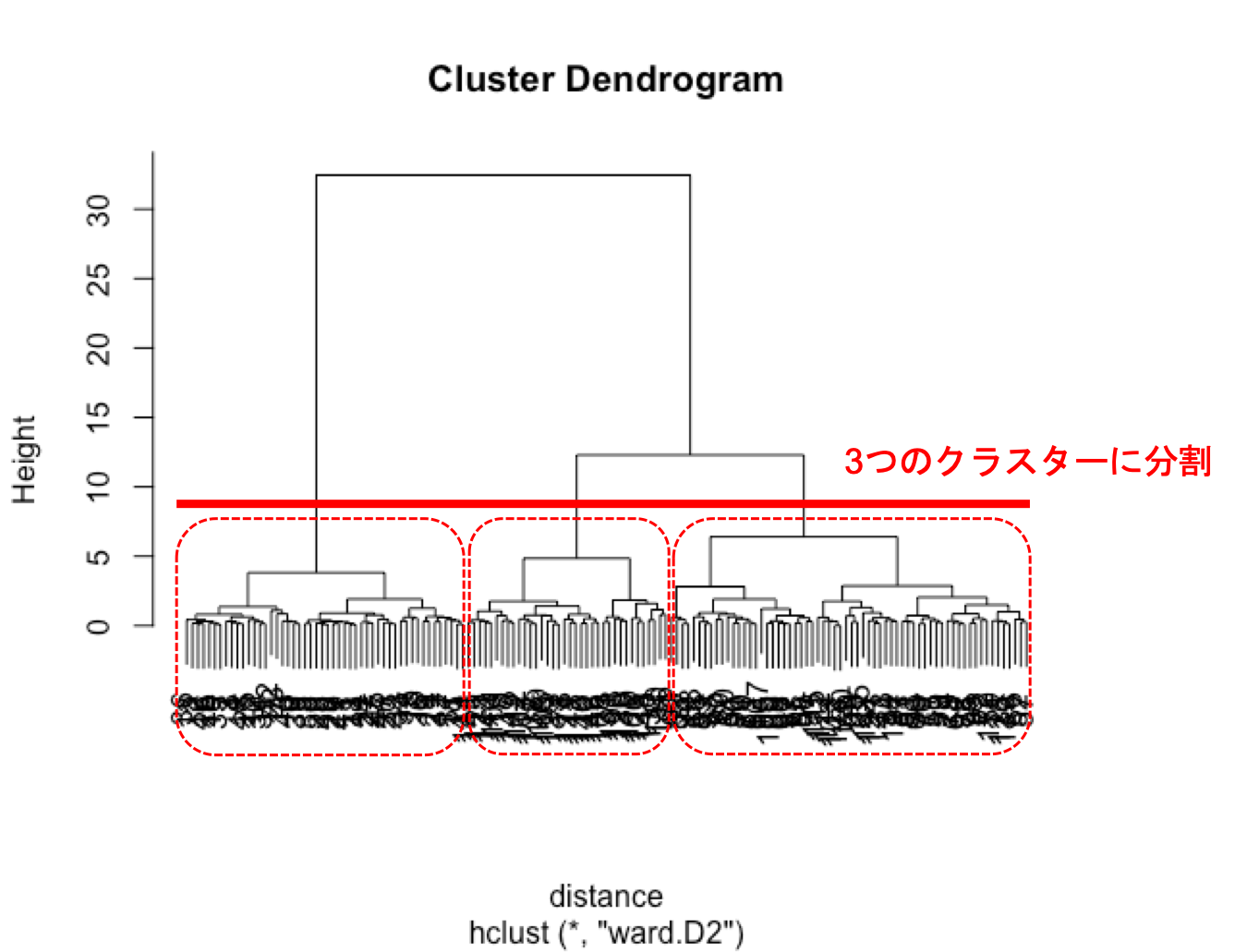
データの分割には関数 cutree を使用します。
関数 cutree の書式と引数は以下の通りです。
cutree(tree, k = NULL, h = NULL)
| 引数 | 説明 |
|---|---|
| tree | 関数 hclust で作成された樹形図 |
| k | 分割するクラスター数 |
| h | 樹形図を分割する高さ |
実際に関数 cutree を実行します。
引数treeには、先ほど作成した樹形図 hc を指定します。
今回は、3つのクラスターに分割したいので、引数 k の値は 3 とします。
# 3つのクラスターに分ける
> result <- cutree(hc,k=3)
データを3つのクラスターに分割した結果を確認します。
> result
[1] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
[36] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
[71] 2 2 2 2 2 2 2 3 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 3 2 3 3 3
[106] 3 2 3 3 3 3 3 3 2 2 3 3 3 3 2 3 2 3 2 3 3 2 2 3 3 3 3 3 2 2 3 3 3 2 3
[141] 3 3 2 3 3 3 2 3 3 2
データが 1,2,3 の3つのクラスターに振り分けられていることがわかります。
最後に、irisデータの5列目 Species のデータを 変数 answer に代入し、品種とクラスタリング結果のクロス表を作成し、分類精度を確認します。
# 精度確認
> answer <- iris[,5]
> table <- table(answer, result)
> table
result
answer 1 2 3
setosa 50 0 0
versicolor 0 49 1
virginica 0 15 35
クロス表から、150サンプル中 (50+49+35=)134サンプルを正確に分類できたことがわかります。
5-2. 非階層クラスタリング
非階層クラスタリングで、irisデータの分類を行います。
ここでは、k-means法 で非階層クラスタリングします。
k-means法でのクラスタリングは関数 kmeans を使用します。
関数 kmeans はクラスターの分類結果 ($cluster)、クラスターの中心ベクトル ($centers)、各クラスター内の個体数 ($size) などを返します。
関数 kmeans の書式と引数は以下の通りです。
> kmeans(x, centers, iter.max = 10, nstart = 1,algorithm = c("Hartigan-Wong", "Lloyd", "Forgy", "MacQueen"))
| 引数 | 説明 |
|---|---|
| x | データ |
| centers | クラスターの数、または クラスターの中心. クラスタの数であれば、 クラスターの中心はランダムに与えられる |
| iter.max | 処理の繰り返し回数 の最大値 |
| nstart | ランダムに初期値を設定する時のパラメータ |
| algorithm | 計算アルゴリズム. ("Hartigan-Wong", "Lloyd", "Forgy", "MacQueen") . デフォルトは "Hartigan-Wong" |
実際に関数 kmeans を実行します。
引数 x に、irisデータを代入した変数 data を指定します。
クラスターを3つに分割したいので、引数 centers には 3 を指定します。
> km <- kmeans(data,3)
関数 kmeans の実行後、km$cluster にクラスターの分類結果が記録されます。
km$cluster を確認します。
> result <- km$cluster
> result
[1] 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
[36] 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 2 2 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
[71] 2 2 2 2 2 2 2 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 1 2 1 1 1
[106] 1 2 1 1 1 1 1 1 2 2 1 1 1 1 2 1 2 1 2 1 1 2 2 1 1 1 1 1 2 1 1 1 1 2 1
[141] 1 1 2 1 1 1 2 1 1 2
データが 1,2,3 の3つのクラスターに振り分けられていることがわかります。
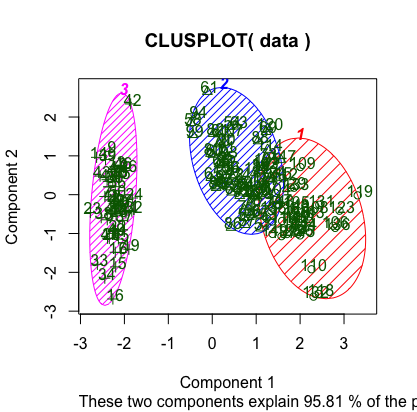
clusterパッケージを読み込み、 クラスタリング結果をプロットします。
> library(cluster)
> clusplot(data, km$cluster, color=TRUE, shade=TRUE, labels=2, lines=0)
最後に、irisデータの5列目 Species のデータを 変数 answer に代入し、品種とクラスタリング結果のクロス表を作成し、分類精度を確認します。
> answer <- iris[,5]
> table <- table(answer, result)
> table
result
answer 1 2 3
setosa 0 0 50
versicolor 2 48 0
virginica 36 14 0
クロス表から、150サンプル中 (50+48+36=)134サンプルを正確に分類できたことがわかります。
6. おわりに
今回は、Rによるクラスタリング実行方法について紹介しました。
わかりやすさの為、あらかじめRに準備されているアヤメデータを用いましたが、CSVファイルなどの外部ファイルからデータを読み込ませて分析を行うこともできます。
もちろん、Rではクラスタリング以外にも様々な手法を用いた分析を行うことができます。
インターネット上にも、調べてみるとたくさん情報があるので、色々試してみると面白いかと思います。
参考情報
R公式サイト
https://www.r-project.org/about.html
R 基本統計関数マニュアル
https://cran.r-project.org/doc/contrib/manuals-jp/Mase-Rstatman.pdf