はじめに
統計学で不偏ではない推定量という困った推定量が有ります 1。この推定量の期待値は標本をどれだけ準備しても正しい値に収束してくれません。このずれ、つまりバイアスをジャックナイフ法という手法で推定してあげて、推定量に補正を加えてあげます。これによって我々の統計的推定の生活がより豊かになるでしょう。
本音
MATLAB の jackknife のドキュメンテーションが貧弱だったので書いてみたというわけです。プログラミング自体は非常に簡単であっさり1行。さすが MATLAB という感じ。
ジャックナイフ推定量 2
無作為標本から得られた母数 $\theta$ の推定量 $\hat{\theta}$ が不偏ではないとき、得られている標本を再利用して、推定量 $\hat{\theta}$ のバイアスを減少させる方法の1つ。以下の方法で求めた推定量をジャックナイフ推定量 ${\hat{\theta} }_{\textrm{jack}}$ と言う。
標本 $X_1 ,\ldots,X_n$ を基にした母数 $\theta$ の推定量 $\hat{\theta}$ において、標本 $X_i$ を除いたサイズ $n-1$ の部分標本から同じように計算される推定量を ${\hat{\theta} }_{(i)}$ と書くことにする。ここから得られた推定量の平均を
{\hat{\theta} }_{(.)} \equiv \frac{1}{n}\sum_{i=1}^n {\hat{\theta} }_{(i)}
と定義する。この時、推定量 $\hat{\theta}$ のバイアスは
\hat{{\mathrm{b}\mathrm{i}\mathrm{a}\mathrm{s}}} \equiv (n-1)({\hat{\theta} }_{(.)} -\hat{\theta} )
で推定することができ、従って元の推定量 $\hat{\theta}$ からバイアスを補正したジャックナイフ推定量 ${\hat{\theta} }_{\textrm{jack}}$ は以下のように得られる:
$$ {\hat{\theta} }_{\textrm{jack}} \equiv \hat{\theta} -\hat{\textrm{bias}} . $$
このようにジャックナイフ法は得られている標本からの部分標本を用いることにより推定精度を向上させることができる。
参考
推定量の標準誤差のジャックナイフ推定量
標準誤差とは統計的推定量のばらつき (精度) を表すものです。この標準誤差についてもジャックナイフ推定量を構成することができ、
{\hat{\textrm{se}} }_{\textrm{jack}} =\sqrt{\frac{n-1}{n}\sum_{i=1}^n {\Bigl({\hat{\theta} }_{(i)} -{\hat{\theta} }_{(.)} \Bigr)}^2 }
を用いてバイアスを取り除くことができる。
例: 最尤推定法で得られる分散のバイアスをジャックナイフ法で推定する
分散 $\sigma^2 =25$ 、平均 $\mu =0$ の正規分布に従う確率変数 $X$ の標本 $\lbrace x_1 ,\ldots,x_{100} \rbrace$ を100個サンプルする。
rng("default");
sigma = 5; % std
n = 200; % number of samples
X = normrnd(0,sigma,n,1); % Sampling from the Normal distribution
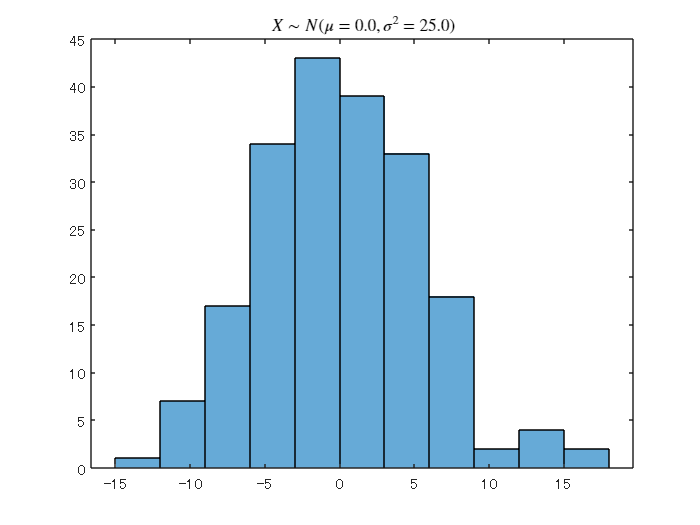
標本をヒストグラムで確認。タイトルは latex 仕様です。:
histogram(X);
title(sprintf(" $X \\sim N(\\mu=%.1f, \\sigma^2=%.1f)$ ",0,sigma^2),'interpreter','latex')
さて、最尤推定法で求められる分散の推定量
{\hat{\sigma^2 } }_{ML} =\frac{1}{n}\sum_{i=1}^n (x_i -{\hat{\mu} }_{ML} )^2
は不偏推定量であることは有名で、この期待値は
{\mathrm{E}}[{\hat{\sigma^2 } }_{ML} ]=\sigma^2 -\frac{1}{n}\sigma^2
であるため、 $-\frac{1}{n}\sigma^2$ のバイアスが有ることが知られている。この不偏推定量を $\hat{\theta} ={\hat{\sigma^2 } }_{ML}$ としてジャックナイフ法を用いて、解析的に知られているバイアスをどの程度上手く推定できるのかを試してみる。
まずは不偏推定量を計算:
theta_hat = var(X,1) % biased estimator
theta_hat = 29.4606
この解析的なバイアスは上記で述べた通り $-\frac{1}{n}\sigma^2$ として既知:
bias = -sigma^2/n % known bias formula
bias = -0.1250
注意
ちなみに分散を計算する関数は var であるが、この var 関数の 2つめの引数を
var(X,1)
とすることで、 $\frac{1}{n}\sum (x_i -\hat{\mu} )^2$ で計算を行う。デフォルトでは不偏推定量である $\frac{1}{n-1}\sum (x_i -\hat{\mu} )^2$ で計算を行うので注意が必要。
次に $\hat{{\mathrm{b}\mathrm{i}\mathrm{a}\mathrm{s}}} =(n-1)({\hat{\theta} }_{(.)} -\hat{\theta} )$ を計算する準備に入る。MATLAB では専用の関数が用意されており
jacknife("統計量を計算する関数 fun","fun への引数1", "fun への引数2", "..." )
を用いて
{\hat{\theta} }_{(.)} \equiv \frac{1}{n}\sum_{i=1}^n {\hat{\theta} }_{(i)}
求める:
theta_hat_dot = jackknife(@var,X,1);
これより、 $\hat{{\mathrm{b}\mathrm{i}\mathrm{a}\mathrm{s}}} =(n-1)({\hat{\theta} }_{(.)} -\hat{\theta} )$ からバイアスを推定することができ:
bias_hat = (n-1)*(mean(theta_hat_dot)-var(X,1)); % jackknife bias estimate
これを解析的なバイアスと比較をすると
array2table([bias, bias_hat],'VariableNames',["Analytical Bias","Bias by Jackknife"])
| Analytical Bias | Bias by Jackknife | |
|---|---|---|
| 1 | -0.1250 | -0.1480 |
非常に近いことが分かる。これを使ってジャックナイフ推定量が以下のように求まる:
theta_hat_jk = theta_hat - bias_hat;
真の分散と分散の最尤推定量、ジャックナイフ推定量を比較すると
array2table([sigma^2,theta_hat,theta_hat_jk],'VariableNames',["Sigma^2","Sigma^2_ML","Sigma^2_JK"])
| Sigma^2 | Sigma^2_ML | Sigma^2_JK | |
|---|---|---|---|
| 1 | 25 | 29.4606 | 29.6087 |
場合によっては改善しないんですね ww
-
重大な Typo をしていました。不偏推定量 --> 不偏ではない推定量 と訂正しました (2024/03/01) ↩
-
統計学実践ワークブック 参照 ↩