2つの整数の最大公約数(greatest common divisor; GCD)を求めるシンプルで効率的なアルゴリズム「ユークリッドの互除法」について、原始的な方法から始めて普段触れられない内容まで発展させる。
TL;DR
ユークリッドの互除法は自然数同士の最大公約数を求める方法と言われるが、わずかな工夫で整数同士の最大公約数が求められる。
# include <stdlib.h>
int gcd(int a, int b) {
if (b == 0) return abs(a);
return gcd(b, a % b);
}
- gcdの引数に条件は不要
- 0や負の数も処理可能
- ※ 実装上は、absが正しい値を返さない場合だけは未定義
- 引数の大小関係を見て入れ換える必要なし
- 0や負の数も処理可能
- 再帰の基本ケースを工夫
- 条件は引数が0のとき(ゼロ除算回避) → 0にも対応
- 戻り値に絶対値を作用 → 負の数にも対応
- 負の数が絡む剰余については言語の差異を考慮不要
内容
毎回数学的な説明に沿って実装し直すのではなく、ひとつの実装から出発してコードの効率化・拡張を進めていく。
- 引き算だけで実装
- 剰余に変えて効率化
- 0も扱えるように改良
- 負の数も扱えるように改良
- 最悪計算量を見積もり、それを突破する裏技を検討
- 再帰を除去
以下の内容は扱わない。
- 最大公約数の説明
- 互除法の証明
- binary GCD
- 拡張互除法
- 有理数や多項式などへの拡張
ちなみに、いくつかの事柄は記事「再帰的なアルゴリズムの実例集」でも触れた。しかしそこでは書き足りなかったので独立した記事にした。
コードの下準備
互除法を何度も実装するにあたり、動作確認するために必要な共通部分は括り出しておく。ファイル "gcd" の中身を以降で実装する1。
# include <stdio.h>
# include <stdlib.h>
# include <assert.h>
int gcd(int a, int b);
# include "gcd"
int main(void) {
while (1) {
int a, b;
printf("input a, b: ");
if (scanf("%d%*[^-+0-9]%d", &a, &b) < 2) break;
printf("gcd(%d, %d) = %d\n", a, b, gcd(a, b));
}
printf("exit.\n");
return 0;
}
コンパイルから実行までの流れは以下の通り。
$ ls
gcd main.c
$ gcc main.c
$ ./a.out # EOF (Ctrl+D) で終了
input a, b: 1920 1080
gcd(1920, 1080) = 120
input a, b: ^D
exit.
自然数を扱う
ここで言う自然数は「正の整数」とする。0は含まない。
そもそもユークリッドの時代に0の概念は無かったはず。以下の実装では「引数が自然数であることのチェック」と「割り切れることの判定」にのみ0が登場する。
引き算による方法
最も単純な方法。初めからループで考えても難しくないが、再帰的に考えてより小さな問題に変形していく。
-
2つの自然数 a, b の最大公約数は、片方を差分 |a-b| に置き換えても同じ
- a, b のうち大きいほうを差分に置き換えると問題が小さくなる: a > b なら gcd(a, b) = gcd(a-b, b)
- 図形的に考えると、2数を辺の長さとする長方形から正方形を切り抜いて新しい小さな長方形を作る
- a, b が等しければそれが最大公約数
- 図形的には正方形であり、しかも元の長方形をぴったり埋め尽くせる最大サイズ
int gcd(int a, int b) {
assert(a > 0 && b > 0);
if (a == b) {
return a;
} else if (a > b) {
return gcd(a - b, b);
} else { /* a < b */
return gcd(a, b - a);
}
}
再帰的なので関数は何度も呼び出される。その引数を出力してみると、例えば gcd(1920, 1080) は以下のように動作する。
| a | b | if文 |
|---|---|---|
| 1920 | 1080 | a > b |
| 840 | 1080 | a < b |
| 840 | 240 | a > b |
| 600 | 240 | a > b |
| 360 | 240 | a > b |
| 120 | 240 | a < b |
| 120 | 120 | a==b |
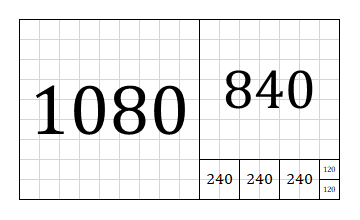
図形で表すと以下の通り。最初は 1920x1080 の長方形で、短辺の大きさに合わせて左上から正方形を取り除くと 840x1080 の新しい長方形ができる。それを繰り返すと最後は右下に 120x120 の正方形が残り、最大公約数を表している。
引き算から効率化
引き算で減らしていくのは、結局、大小関係が逆転するまで同じ引き算を続けるということになる。これは剰余を求めることで一発で完了する。ただし割り切れる場合は引き算をしすぎて0になってしまうので、再帰呼び出しはせず除数を返すようにする。
int gcd(int a, int b) {
assert(a > 0 && b > 0);
if (a == b) {
return a;
} else if (a > b) {
if (a % b == 0) return b;
return gcd(a % b, b); /* gcd(a - b - ... - b, b)*/
} else { /* a < b */
if (b % a == 0) return a;
return gcd(a, b % a); /* gcd(a, b - a - ... - a)*/
}
}
a == b の場合も割り切れる場合に含まれるので、if文で個別の節にする必要はなくもう少し簡単にできる。
int gcd(int a, int b) {
assert(a > 0 && b > 0);
if (a >= b) {
if (a % b == 0) return b; /* including a == b */
return gcd(a % b, b);
} else { /* a < b */
if (b % a == 0) return a;
return gcd(a, b % a);
}
}
| a | b | if文 |
|---|---|---|
| 1920 | 1080 | a ≧ b |
| 840 | 1080 | a < b |
| 840 | 240 | a ≧ b |
| 120 | 240 | a < b b%a==0 |
無駄な分岐の除去
剰余を求めると一発で引数の大小関係が逆転する。それならif文の a ≧ b と a < b の節は交互に実行されるわけで、毎回分岐させるのは無駄になる。どうにかして無駄を省きたい。
よく見るとどちらの処理も「大きい方を小さい方で割った余りを求める」という同じ処理になっている。ならば引数の大小関係をルール化すれば分岐不要になる。ここでは第1引数が大きいと決めて、再帰呼び出しの際の引数を修正する。
int gcd(int a, int b) {
assert(a > 0 && b > 0);
/* a >= b */
if (a % b == 0) return b;
return gcd(b, a % b); /* b > a % b */
}
| a | b | a%b |
|---|---|---|
| 1920 | 1080 | 840 |
| 1080 | 840 | 240 |
| 840 | 240 | 120 |
| 240 | 120 | 0 |
こうするとユーザーが関数呼び出しするときは a < b が可能になってしまい、 a ≧ b を守れない問題があるように見える。しかし実はそれへの対処は必要ない。実際に試してみると、最初に再帰呼び出しするときに大小関係を直してくれる。
| a | b | a%b |
|---|---|---|
| 1080 | 1920 | 1080 |
| 1920 | 1080 | 840 |
| ... | ... | ... |
| 240 | 120 | 0 |
0も扱う
自然数に比べて考え方が難しいのだが、最大公約数の計算では特別な性質を持っている。
0の約数
0はどんな自然数で割っても余りが出ない。なのであらゆる自然数が 0 の約数となっている2。
すると、ある自然数 a と 0 の最大公約数は a と考えればいい。これが再帰の基本ケースとなる。 b==0 ということはそれ以上再帰しようとするとゼロ除算エラーが発生するので、終了条件として都合がいい。
実装では、 a が 0 で b が自然数ということもありうるので、引数の条件を緩めておく。ひとつ前提に沿わない入力が可能な件は次節で扱う。
int gcd(int a, int b) {
assert(a >= 0 && b >= 0);
if (b == 0) return a;
return gcd(b, a % b);
}
| a | b | a%b |
|---|---|---|
| 1920 | 1080 | 840 |
| 1080 | 840 | 240 |
| 840 | 240 | 120 |
| 240 | 120 | 0 |
| 120 | 0 | - |
0と0の最大公約数
既に実装してしまったが、 a と b が両方 0 なら最大公約数 gcd(0, 0) はどうすればいいだろう? この答えの案はいくつかある。
| gcd(0, 0) = ? | そう考えた理由 |
|---|---|
| 0 | gcd(a, 0) = a を拡大解釈し、 a に素直に 0 を代入すればいい |
| 無限大 | 0の約数はいくらでも大きく選べる |
| 未定義 | もはやまともな意味がつけられない |
最大公約数の本来の意味を考えると無限大が良さそうだが、 0 とするのが簡単であるしそれで滅多に困らない。無限大や未定義を導入すると、整数に収まらないし、3個以上の最大公約数(おまけ参照)を考えるときにそれらに対する演算も考える必要ができてしまう。
これで晴れて「非負整数 a と 0 の最大公約数は a」が成り立つ。二項演算の結果が相手の数になるものを単位元という。(例えば、足し算なら0、掛け算なら1)
注意点
gcd(0, 0) = 0 としたことで困る状況もある。ふつう最大公約数は両引数を割り切ることができるが、0だとゼロ除算エラーを引き起こしてしまう。最小公倍数(LCM)を実装する場合などは要注意3。
int lcm(int a, int b) {
return a / gcd(a, b) * b;
}
(おまけ)n個の数の最大公約数
3個の数の最大公約数を求めるときは、2個の結果と3個目との最大公約数を求めればいい。
\gcd{(a,b,c)} = \gcd{(\gcd{(a,b)},c)}
gcd(0, 0) = 0 と決めたことで、 a=b=0 であっても問題なく計算できる。
n個に増えた場合も同じで、n-1個の結果とn個目との最大公約数を求めればいい。
\gcd{(a_1,\dots,a_{n-1},a_n)} = \gcd{(\gcd{(a_1,\dots,a_{n-1})},a_n)}
すると n≦2 の場合にも拡張できて、最終的に「0個の数の最大公約数は0(単位元)」という結果が得られる。細かい意味はともかくとして、計算を実装する場合はそうしておくのが綺麗。
int gcd_n(int n, int ary[]) {
int i;
int d = 0;
for (i = 0; i < n; i++) d = gcd(ary[i], d);
return d;
}
ちなみに、n個の数の中にひとつでも 1 があれば、あるいはforループの途中で d==1 になれば、最大公約数は 1 になる。考えている問題によってはそこでループを打ち切る処理を入れてもいいかもしれない。
負の整数も扱う
ここまで対応すれば、引数をチェックしていたassertを消すことができる。
なお、実装の際に絶対値関数absを使うので、absが正しい値を返さない INT_MIN = -231 を引数に含むgcdは未定義とする。(その辺の事情は算術オーバーフローの節を参照)
負の数の約数
これは0のときより簡単。負の数を割り切れる整数は正の数を割り切れる整数と全く同じ。なので約数を考えるときに符号を気にする必要は無い。最大公約数の計算では、単純には引数の絶対値をとって計算すればいい。
\gcd{(a,b)} = \gcd{(|a|,|b|)}
int gcd(int a, int b) {
a = abs(a);
b = abs(b);
if (b == 0) return a;
return gcd(b, a % b);
}
絶対値をとる回数の削減
前節の方法では再帰呼び出しの度に引数の絶対値を計算していて無駄に感じる。実は毎回絶対値を計算する必要は無く、再帰の基本ケースで絶対値を返すだけで済む。
int gcd(int a, int b) {
if (b == 0) return abs(a);
return gcd(b, a % b);
}
ここで疑問になるのは、剰余の計算で負の数を使うとどうなるのかということ。これは言語によって結果が変わり4、そのため普通は利用を避けることが多い。しかし互除法の場合はどの結果でも正しく計算できるため問題ない。
負の数の剰余の詳細
整数同士の割り算 a ÷ b (b≠0) において商 q と余り r は以下の式を満たす整数である。
a = b q + r
これだと q と r の組み合わせは無数に考えられるため、 r のとれる範囲に条件を置いて一意になるようにする。この条件は a と b が自然数なら 0 ≦ r < b と考えるのが自然であり特に問題ないが、負の数だと意見が分かれる。
| 条件 | 8 % 3 | 8 % (-3) | (-8) % 3 | (-8) % (-3) |
|---|---|---|---|---|
| r は常に正か0 | 2 | 2 | 1 | 1 |
| r の符号は a に合わせる | 2 | 2 | -2 | -2 |
| r の符号は b に合わせる | 2 | -1 | 1 | -2 |
ただしどの立場でも |r| < |b| は守るため、gcdの第2引数の絶対値が小さくなることが保証され再帰的に計算できる。
INT_MIN と算術オーバーフロー
int型での負の整数の表現によく使われる「2の補数」は、正の数より負の数のほうが表せる数がひとつ多い。 INT_MIN = -231 はint型で表せるが、これを符号反転させた 231 はint型で表せない。そのため gcd の引数に INT_MIN があると正しく計算できない可能性がある。(short型やlong型などでも同様の事情がある。任意長整数型なら大丈夫。)
互除法で使用している演算では、まず abs(INT_MIN) が計算できない。この結果はC言語では未定義だが、 231 と同じビットパターンである INT_MIN 自身を返す可能性が高い。エラーにならなければ計算は続けられるものの、 gcd の戻り値がマイナスになる可能性があるため注意。( abs(INT_MIN) == INT_MIN を許しているなら gcd(INT_MIN, 0) == INT_MIN を許してもいい気はする)
もうひとつ、 INT_MIN % (-1) も問題がある。これは数学的には答えが 0 になるので一見大丈夫そうだが、CPUが除算命令を使っていると INT_MIN / (-1) を計算するためエラーになってしまう。コンパイラが対処してくれる可能性があるらしいが、信用できないときは自力で対処しなければならない。
- 剰余計算を安全にするだけなら
a % b→(b == -1 ? 0 : a % b)と置き換える - 最大公約数の計算に向いた対策は、再帰の基本ケースに
if (b == -1) return 1;を追加する
この辺の対策を組み込むとコードが冗長になるので、記事では「引数に INT_MIN があるときの動作は未定義」としている。
最悪計算量
ユークリッドの互除法の効率について、「桁数の5倍以内の再帰回数で済む」という話があり、スタックオーバーフローを特に気にしなくていい根拠になっている。これはどう決まっているのか、そしてもっと減らすことはできないのか見ていく。
最悪ケース
どういうときが最悪で、なぜ回数がかさむのかは、実際に試すとわかりやすい。
| a | b | r | q |
|---|---|---|---|
| 144 | 89 | 55 | 1 |
| 89 | 55 | 34 | 1 |
| 55 | 34 | 21 | 1 |
| 34 | 21 | 13 | 1 |
| 21 | 13 | 8 | 1 |
| 13 | 8 | 5 | 1 |
| 8 | 5 | 3 | 1 |
| 5 | 3 | 2 | 1 |
| 3 | 2 | 1 | 1 |
| 2 | 1 | 0 | 1 |
| 1 | 0 | - | - |
剰余を求める際に商 q も見てみると常に1になっている。このため1回の剰余計算であまり小さくならない。
b などに表れている数列はフィボナッチ数。この数列はおよそ $\phi = \frac{1+\sqrt{5}}{2} \simeq 1.6$ 倍で増えていくので、互除法では再帰1回毎に約1/1.6に減少する。そのため再帰回数は十進桁数の $\log_\phi {10} \simeq 4.8$ 倍程度となる。最悪とは言っても桁数に比例するので十分高速であり、int型の範囲であれば50回もかからない。
絶対値最小剰余による改善
フィボナッチ数の例では、gcdの引数が約1/1.6ずつ小さくなるという遅い変化だった。この倍率が改善されれば再帰が少なく済む。
その方法のヒントは既に得ている。負の数の剰余のところで剰余が負になっても互除法に影響が無いことを見た。すると新しい条件として、**剰余の絶対値が除数の半分以下(最小)**になるように計算することもできる。自然数同士の計算でも剰余が負になりうることに注意。
a = b q + r \quad \left( -\frac{|b|}{2} \le r \lt \frac{|b|}{2} \right)
| 条件 | 8 % 3 | 8 % (-3) | (-8) % 3 | (-8) % (-3) |
|---|---|---|---|---|
| r は常に正か0 | 2 | 2 | 1 | 1 |
| r は絶対値が最小 | -1 | -1 | 1 | 1 |
ふつうの剰余演算はこの方法を採用していないので、剰余を求める関数を適当に自作して使う。
int mod(int a, int b) {
int r = a % b;
if (-r-1 >= (abs(b)-1)/2) r += abs(b);
if ( r > (abs(b)-1)/2) r -= abs(b);
return r;
}
int gcd(int a, int b) {
if (b == 0) return abs(a);
return gcd(b, mod(a, b));
}
これで本当に再帰回数が減るのか見ていく。前節と同じフィボナッチ数で試すと、 b がひとつ飛ばしで小さくなっている。
| a | b | r | q |
|---|---|---|---|
| 144 | 89 | -34 | 2 |
| 89 | -34 | -13 | -3 |
| -34 | -13 | 5 | 3 |
| -13 | 5 | 2 | -3 |
| 5 | 2 | -1 | 3 |
| 2 | -1 | 0 | -2 |
| -1 | 0 | - | - |
最悪ケースは商が常に2になるときで(多分)、ペル数という名前がついている。数列の公比は $\tau = 1+\sqrt{2} \simeq 2.4$ に収束するので再帰回数は十進桁数の $\log_\tau {10} \simeq 2.6$ 倍程度となる。元のアルゴリズムの半分近い回数になっている。
| a | b | r | q |
|---|---|---|---|
| 169 | 70 | 29 | 2 |
| 70 | 29 | 12 | 2 |
| 29 | 12 | 5 | 2 |
| 12 | 5 | 2 | 2 |
| 5 | 2 | -1 | 3 |
| 2 | -1 | 0 | -2 |
| -1 | 0 | - | - |
ただし、計算量のオーダーとして見ると桁数に比例することは変わっていない。また、剰余の計算が複雑になっているので、それを考慮すると再帰1回あたりの処理が重くなりかえって効率が下がっていると考えられる。
再帰の除去
今回実装したものはどれも末尾再帰になっているので、簡単に再帰を除去できる。
goto文
return 関数呼び出し(引数); となっているところを、引数の上書きと先頭へのジャンプに置き換える。
int gcd(int a, int b) {
gcd_top:
if (b == 0) return abs(a);
{
/* a, b = b, a % b */
int r = a % b;
a = b;
b = r;
}
goto gcd_top;
}
while文(無限ループ)
goto文は大げさなのでwhile文で同じ形を実現する。全体を無限ループにしておき、gotoの代わりにcontinueを書けば先頭へのジャンプを再現できる。
int gcd(int a, int b) {
while (1) {
if (b == 0) return abs(a);
{
/* a, b = b, a % b */
int r = a % b;
a = b;
b = r;
}
continue;
}
}
while文(整理)
無限ループの先頭で脱出条件を書いているのなら、否定に変えてwhile文の条件に組み込んでしまえばいい。ついでに、末尾のcontinueも意味ないので除く。
int gcd(int a, int b) {
while (b != 0) {
/* a, b = b, a % b */
int r = a % b;
a = b;
b = r;
}
return abs(a);
}
(おまけ)前処理の追加
記事中では使っていないが、再帰関数をラッパー関数で包んで前処理を入れている場合は、ループの前に同様の処理を入れればいい。
例として、事前に引数を非負整数に直すことで絶対値最小剰余を簡略化してみる。最大公約数で符号は考えなくていいので、剰余が負になるときは符号を反転させる。
int gcd(int a, int b) {
a = abs(a);
b = abs(b);
assert(a >= 0 && b >= 0);
while (b != 0) {
/* a, b = b, abs(mod(a, b)) */
int r = a % b; /* 0 <= r < b */
if (r > b/2) r = b - r;
a = b;
b = r;
}
return a;
}
参考
Wikipedia英語版に色々とヒントをもらった。